Consistency of the φ-Divergence Based Change Point Estimator

Mwelu Susan¹, Anthony G. Waititu², Peter N. Mwita³, Charity Wamwea²

¹Pan-African University Institute of Basic Sciences, Technology and Innovation, Nairobi, Kenya.
²Department of Statistics and Actuarial Sciences, JKUAT, Nairobi, Kenya.
³Department of Mathematics, Statistics and Actuarial Sciences, Machakos University, Machakos, Kenya.

DOI: 10.4236/ojs.2020.105048                

Abstract

This paper utilizes a change-point estimator based on the φ-divergence. Since we seek a near perfect translation to reality, then locations of parameter change within a finite set of data have to be accounted for since the assumption of stationary model is too restrictive especially for long time series. The estimator is shown to be consistent through asymptotic theory and finally proven through simulations. The estimator is applied to the generalized Pareto distribution to estimate changes in the scale and shape parameters.

Keywords

Change Point, Consistency, φ-Divergence, Kullback-Leibler, Generalized Pareto Distribution

1. Introduction

Let $x_1,\cdots ,x_n$ be a time series of size n. Methods in literature consider stationary models in explaining the underlying data generating process. However, stationarity is arguably a very strong assumption in many real-world applications as process characteristics evolve over time. Reviewed literature reveals that the use of one model may not be appropriate to model a non-stationary series and as such various change-point estimation methods have been proposed. However, they are limited in different ways and their suitability depends on the underlying assumptions. Statistical research works have shown that with time, the underlying data generating processes undergo occasional sudden changes [1]. A change point is said to occur when there exists a time $\tau \in \left\{1,\cdots ,n-1\right\}$ such that the statistical properties of $x_1,\cdots ,x_{\tau }$ and $x_{\tau +1},\cdots ,x_n$ are different. In its simplest form, change-point detection is the name given to the problem of estimating the point at which the statistical properties of a sequence of observations change [2]. The overall behavior of observations can change over time due to internal systemic changes in distribution dynamics or due to external factors. Time series data entail changes in the dependence structure and therefore modelling non-stationary processes using stationary methods to capture their time-evolving dependence aspects will most likely result in a crude approximation as abrupt changes fail to be accounted for [3]. Each change point is an integer between 1 and n − 1 inclusive. The process X is assumed to be piece-wise stationary implying that some characteristics of the process change abruptly at unknown points in time. The corresponding segments are then said to be homogeneous within but each of the subsequent segments is heterogeneous in characteristics. For a parametric model the parameters associated with the i^th segment denoted ${\theta }_i$, are assumed to contain changes. Parametric tests for change point are mainly based on the likelihood ratio statistics and estimation based on the maximum likelihood method whose general results can be found in [4].

Detection of change points is critical to statistical inference as a near perfect translation to reality is sought through model selection and parameter estimation. Parametric methods assume models for a given set of empirical data. Within a parametric setting change, points can be attributed to change in the parameters of the underlying data distribution. Generally, change point methods can be compared based on general characteristics and properties such as test size, power of the test or the rate of convergence to estimate the correct number of change point and the change-point locations. Change point problems can be classified as off-line which deals with only a fixed sample or on-line which considers new information as it observed. Off-line change point problems deal with fixed sample sizes which are first observed and then detection and estimation of change points are done. [5] introduced the change point problem within the off-line setting. Since this pioneering work, methodologies used for change point detection have been widely researched on with methods extending to techniques for higher order moments within time series data. Ideally, it is desired to test how many change points are present within a given set of data and to estimate the parameters associated with each segment. If τ is known then the two samples only need to be compared. However, if τ is unknown then it has to be analyzed through change point analysis that entails both detection and estimation of the change point/change time. The null hypothesis of no change against the alternative that there exists a time when the distribution characteristics of the series changed is then tested. Stationarity in the strict sense, implies time-invariance of the distribution underlying the process.

The hypotheses would be stated as:

$\begin{array}{l}{H}_0:F\left(x;\theta \right)=F\left(x;{\theta }_1\right)\text{for}t=1,\cdots ,n\\ H_1:F\left(x;\theta \right)=\{\begin{array}{l}F\left(x;{\theta }_1\right)\text{for}t=1,\cdots ,\tau \\ F\left(x;{\theta }_2\right)\text{for}t=\tau +1,\cdots ,n\end{array}\end{array}$ (1)

The null hypothesis postulates that the distribution remains unchanged throughout within the sample of size n whereas the alternative postulates no change as in the null up to time τ when change occurs. Then the change point problem is to test the hypotheses about the population parameter(s)

$H_0:{\theta }_1={\theta }_2=\cdots ={\theta }_n\text{versus}{H}_1:{\theta }_1=\cdots ={\theta }_{\tau }\ne {\theta }_{\tau +1}=\cdots ={\theta }_n$ (2)

where τ is unknown and needs to be estimated. If $\tau <n$ then the process distribution has changed and τ is referred to as the change point. We assume that there exists $\lambda \in \left[0,1\right]$ such that τ satisfies

$\tau =\lambda n$ (3)

where n is the number of observations in a given data set. Then hypothesis 2 can be restated as

$\begin{array}{l}{H}_0:\tau =n,\left(\lambda =1\right)\\ H_1:\tau <n,\left(0<\lambda <1\right)\end{array}$ (4)

At a given level of significance, if the null hypothesis is rejected, then the process X is said to be locally piecewise-stationary and can be approximated by a sequence of stationary processes that may share certain features such as the general functional form of the distribution F. Many authors such as [6] - [11] have considered both parametric and non-parametric methods of change point detection in time series data. Ideally, change points cannot be assumed to be known in advance hence the need for various methods of detection and estimation.

This paper is organized as follows: Section 2 gives an overview of the change point estimator based on a pseudo-distance measure. Section 3 provides key results for consistency of the estimator. Section 4 provides an application of the change point estimator to the shape and scale parameters of the generalized Pareto distribution. Section 5 gives an application of the estimator and consistency is shown through simulations. Finally 6 provides concluding remarks.

2. Change Point Estimator

The change point problem is addressed by using a “distance” function between distributions to describe the change. Given a distance function, a test statistic is constructed to guarantee a distance $>ϵ\left(ϵ\ge 0\right)$ between any two distributions based on a sample size n. Consider a given parametric model $f_{\theta }:\theta \in \Theta$ where Θ is the parameter space defined on a data set of size n. Let $X_1,\cdots ,X_n$ be random variables and have probability densities $f\left(x;{\theta }_1\right),\cdots ,f\left(x;{\theta }_n\right)$ with respect to σ-finite measure µ with $F\left(x;\theta \right)$ generating distinct measures if $\theta \in \Theta$

Definition 2.1 ( $\varphi$ -divergence). Let $F_{{\theta }_1}$ and $F_{{\theta }_2}$ be two probability distributions. Define the $\varphi$ -divergence between the two distributions as

$D_{\varphi }\left(F_{{\theta }_1},F_{{\theta }_2}\right)=D_{\varphi }\left({\theta }_1,{\theta }_2\right)$

The broader family of $\varphi$ -divergences that take the general form

$D_{\varphi }\left({\theta }_1,{\theta }_2\right)={\displaystyle \int \varphi \left(\frac{\text{d}{F}_{{\theta }_1}}{\text{d}{F}_{{\theta }_2}}\right)\text{d}{F}_{{\theta }_2}}$

$\begin{array}{c}={\displaystyle \int f_{{\theta }_2}\left(x\right)\varphi \left(\frac{f_{{\theta }_1}\left(x\right)}{f_{{\theta }_2}\left(x\right)}\right)\text{d}\mu \left(x\right)}\\ =E_{{\theta }_2}\left[\varphi \left(\frac{f_{{\theta }_1}\left(x\right)}{f_{{\theta }_2}\left(x\right)}\right)\right],\varphi \in \Phi \end{array}$ (5)

where $\Phi$ is the class of all convex functions $\varphi \left(t\right),t>0$ satisfying $\varphi \left(1\right)=0,{\varphi }^{″}\left(1\right)>0$.

Assumption 1. The function $\varphi \in \Phi :\left[0,\infty \right)\to \left(-\infty ,+\infty \right)$ is convex and continuous. The restriction on $\left[0,\infty \right)$ is finite, twice continuously differentiable with $\varphi \left(1\right)={\varphi }^{\prime }\left(1\right)=0,{\varphi }^{″}\left(1\right)=1$.

At any point t = 0, to avoid indeterminate expressions [12] gives the following assumptions in relation to the functions $\varphi$ involved in the general definition of $\varphi$ -divergence statistics,

$\begin{array}{l}0\varphi \left(\frac{0}{0}\right)=0\\ 0\varphi \left(\frac{p}{0}\right)=\underset{u\to \infty }{\lim }\frac{\varphi \left(u\right)}{u}\end{array}$ (6)

These assumptions ensure the existence of the integrals. Different choices of φ result in many divergences that play important roles in statistics including the Kullback-Leibler $\varphi \left(t\right)=-\ln \left(t\right)$, total variation $\varphi \left(t\right)=\left|t-1\right|$ among others. $D_{\varphi }\left({\theta }_1,{\theta }_2\right)\ne D_{\varphi }\left({\theta }_2,{\theta }_1\right)$ hence divergence measures are not distance measures but give some difference between two probability measures hence the term “pseudo-distance”. More generally a divergence measure is a function of two probability density (or distribution) functions, which has non-negative values and takes the value zero only when the two arguments (distributions) are the same. A divergence measure grows larger as two distributions are further apart. Hence, a large divergence implies departure from the null hypothesis.

Generally, a change point problem’s objective would be to propose an estimator for the possible change-point τ given a set of random variables.

Based on the divergence in 5 then a change point estimator can be constructed as;

$D_{n\tau }=\underset{1<\tau <n}{\max }\left(\lambda \left(1-\lambda \right)\right)\frac{2}{{\varphi }^{″}\left(1\right)}{D}_{\varphi }\left({\theta }_1,{\theta }_2\right)$ (7)

where $\lambda =\frac{\tau }{n}\in \Lambda :\Lambda =\left[0,1\right]$ and $\widehat{{\theta }_1},\widehat{{\theta }_2}$ are the maximum likelihood estimates of the parameters before and after the change point.

To test for the possibility of having a change in distribution of $x_1,\cdots ,x_n$ it is natural to compare the distribution function of the first τ observations to that of the last (n − τ) since the location of the change time is unknown. When τ is near the boundary points, say near 1 or near n then we are required to compare an estimation calculated on a correct large number of observations (n − τ) to an estimation from a small number of observations τ. This may result to an erratic behavior of the test statistic [7] due to instability of the estimators of the parameters. If λ is not bounded away from zero and one, then the test statistic does not converge in distribution i.e. the critical values for the test statistic diverge to infinity as n → ∞ to obtain a sequence of level α tests [13]. However, fixed critical values can be obtained for increasing sample sizes when λ is bounded away from zero and one and yields significant power gains if the change point is in Λ.

Let ε > 0 be small enough such that $\lambda \in \left(ϵ,1-ϵ\right)$

Suppose that λ maximizes the test statistic over [0, 1] then under the null hypothesis,

$\begin{array}{l}{\sup }_{\lambda \in \left(ϵ,1-ϵ\right)}D\left(\lambda \right)=O_p\left(1\right)\forall ϵ\\ {\sup }_{\lambda \in \left[0,1\right]}D\left(\lambda \right)\to \infty \text{as}n\to \infty \end{array}$ (8)

[13]. By this result and for $N\left(ϵ\right)=ϵn,\cdots ,\left(1-ϵ\right)n$ then the test statistic becomes,

$D_{n\tau }=\underset{\tau \in N\left(ϵ\right)}{\max }\left(\frac{\tau }{n}\left(1-\frac{\tau }{n}\right)\right)\frac{2}{{\varphi }^{″}\left(1\right)}{D}_{\varphi }\left({\theta }_1,{\theta }_2\right)$ (9)

The change-point estimator $\hat{\tau }$ of a change point τ is the point at which there is maximal sample evidence for a change in distributional parameters characterized by maximum divergence. It is estimated by the least value of τ that maximizes the test statistic 9.

$\hat{\tau }=\min \left\{\tau :D_{n\tau }=\underset{\tau \in N\left(ϵ\right)}{\max }\left(\frac{\tau }{n}\left(1-\frac{\tau }{n}\right)\right)\frac{2}{{\varphi }^{″}\left(1\right)}{D}_{\varphi }\left({\theta }_1,{\theta }_2\right)\right\}$ (10)

3. Consistency of the Change Point Estimator

A minimal requirement for a good statistical decision rule is its increasing reliability with increasing sample sizes [14].

Let $x_1,\cdots ,x_n$ be a sample of fixed size n with the density function $f\left(x;\theta \right)$ for $\theta \in \Theta \subset R^d$ and $L\left(x;\theta \right)$ be the likelihood function. It can be shown that by Taylor’s theorem under the null hypothesis, the $\varphi$, divergence based estimator can be reduced to a two-sample Wald-type test statistic of the form

$\widehat{W_{n\tau }}=\underset{\tau \in N\left(ϵ\right)}{\max }\left(\frac{\tau }{n}\left(1-\frac{\tau }{n}\right)\right)\left(\widehat{{\theta }_1}-{\theta }_1\right)I\left({\theta }_0\right)\left(\widehat{{\theta }_2}-{\theta }_2\right)$ (11)

Suppose $x_1,\cdots ,x_n$ are iid random variables of size n with probability density function $f\left(x;\theta \right)$ with $\theta ={\left({\theta }_1,\cdots ,{\theta }_k\right)}^{\prime },k<n$ being the vector of parameters governing the pdf. The likelihood function can be expressed as

$L\left(\theta |x\right)={\displaystyle \underset{i=1}{\overset{n}{\prod }}f\left(x_i;\theta \right)}$ (12)

It is more convenient to work with the logarithm of the likelihood function given by

$\mathcal{l}\left(\theta |x\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}\log f\left(x_i;\theta \right)}$ (13)

Since the logarithm is a monotone increasing function, maximizing the likelihood function is equivalent to maximizing the log-likelihood function. Introduce the following notations:

${\nabla }_{\theta }\log f\left(x_i;\theta \right)=\frac{\partial }{\partial \theta }\log f\left(x_i;\theta \right)$ (14)

${\nabla }_{\theta }^2\log f\left(x_i;\theta \right)=\frac{{\partial }^2}{\partial {\theta }_i\partial {\theta }_j}\log f\left(x_i;\theta \right)$ (15)

$H_n\left(\theta \right)=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\nabla }_{\theta }^2\log f\left(x_i;\theta \right)}$ (16)

$U_{jm}\left(\theta \right)={\displaystyle \underset{i=j}{\overset{m}{\sum }}{\nabla }_{\theta }\log f}\left(x_i;\theta \right),1\le j\le m\le n$ (17)

The following equalities hold as $n\to \infty$.

$\begin{array}{l}{H}_n\left(\theta \right)\to -I\left(\theta \right)\\ H_n\left(\theta \right)+\frac{1}{n}I\left(\theta \right)\to 0\end{array}$ (18)

On assumption that ${\theta }_1\ne {\theta }_2$ for ${\theta }_1,{\theta }_2\in \Theta \subset R^d$, then

$\begin{array}{l}\widehat{{\theta }_1}\to {\theta }_1,\widehat{{\theta }_2}\to {\theta }_2\text{as}n\to \infty \\ \widehat{{\theta }_1}\text{and}\widehat{{\theta }_2}\text{aresolutionsto}\\ {\displaystyle \underset{i=1}{\overset{\tau }{\sum }}{\nabla }_{\theta }\log f\left(x_i;\theta \right)}=0\text{and}{\displaystyle \underset{i=\tau +1}{\overset{n}{\sum }}{\nabla }_{\theta }\log f\left(x_i;\theta \right)}=0\text{respectively}.\end{array}$ (19)

Theorem 3.1. Let $0<{\delta }_1<{\delta }_2<\infty ,n_1=n{\delta }_1,n_2=n{\delta }_2$

$\underset{\tau \to \infty }{\lim }\max \left\{\Vert {\tau }^{-\frac{1}{2}}{U}_{\tau }\left({\theta }_0\right)\Vert :n_1<\tau <n_2\right\}=O_p\left(1\right)$ (20)

Theorem 3.2. Let $0<ϵ<1-ϵ$ for $ϵ>0$ small enough. Then as $n\to \infty$

$\max \left\{\Vert {\tau }^{-\frac{1}{2}}I{\left({\theta }_0\right)}^{-1}{U}_{n\tau }\left({\theta }_0\right)\Vert :\tau \in N\left(ϵ\right)\right\}=O_p\left(1\right)$ (21)

For the proof of theorems 3.1 and 3.2 see [15].

Theorem 3.3. Let $0<{\delta }_1<{\delta }_2<\infty$ and $n_1=n{\delta }_1,n_2=n{\delta }_2$ For $n\ge 1$

$\underset{n\to \infty }{\lim }\left\{\max \left[n^{1/2}\Vert \left(\widehat{{\theta }_n}-{\theta }_0\right)-\frac{1}{n}I{\left({\theta }_0\right)}^{-1}{U}_n\left({\theta }_0\right)\Vert :n_1<n_2\right]\right\}\to 0$ (22)

Proof

$\begin{array}{c}0=U_n\left(\widehat{{\theta }_n}\right)=U_n\left({\theta }_0\right)+\left(\widehat{{\theta }_n}-{\theta }_0\right){U^{\prime }}_n\left({\theta }_0\right)+\frac{1}{2}{\left(\widehat{{\theta }_n}-{\theta }_0\right)}^2{U^{‴}}_n\left({\theta }_0\right)\\ =U_n\left({\theta }_0\right)-n{H}_n\left({\theta }_0\right)+\tilde{R}\\ =n^{-\frac{1}{2}}{U}_n\left({\theta }_0\right)-n{H}_n\left({\theta }_0\right)n^{-\frac{1}{2}}\left(\widehat{{\theta }_n}-{\theta }_0\right)+n^{-\frac{1}{2}}\tilde{R}\end{array}$ (23)

The third term on the RHS is $o_p\left(1\right)$ [14]. By definition of MLE $U_n\left(\widehat{{\theta }_n}\right)=0$.

$U_n\left({\theta }_0\right)=-n{H}_n\left({\theta }_n\right)\left(\widehat{{\theta }_n}-{\theta }_0\right)n^{-\frac{1}{2}}{U}_n\left({\theta }_0\right)=-n^{\frac{1}{2}}{H}_n\left({\theta }_0\right)\left(\widehat{{\theta }_n}-{\theta }_0\right)$ (24)

From Equation (24) we obtain

$n^{\frac{1}{2}}\left(\widehat{{\theta }_n}-{\theta }_0\right)=-n^{\frac{1}{2}}{H}_n{\left({\theta }_0\right)}^{-1}{U}_n(\; \theta \; 0\; )$

Hence

$n^{\frac{1}{2}}\Vert \left(\widehat{{\theta }_n}-{\theta }_0\right)-\frac{1}{n}I{\left({\theta }_0\right)}^{-1}{U}_n\left({\theta }_0\right)\Vert \le \Vert -H_n{\left({\theta }_0\right)}^{-1}I\left({\theta }_0\right)\Vert \Vert n^{-\frac{1}{2}}{U}_n\left({\theta }_0\right)\Vert$ (25)

But by Equation (18)

$\Vert -H_n{\left({\theta }_0\right)}^{-1}I\left({\theta }_0\right)\Vert \to 0$

By theorem 3.1 $\Vert n^{-\frac{1}{2}}{U}_n\left({\theta }_0\right)\Vert$ is bounded in probability. Hence the proof.

Theorem 3.4. Let $0<ϵ<1-ϵ$ for $ϵ>0$ small enough. Then

$\underset{n\to \infty }{\lim }\left\{\max \left[{\tau }^{1/2}\Vert \left(\widehat{{\theta }_1}-\widehat{{\theta }_2}\right)-\frac{n}{\tau \left(n-\tau \right)}I{\left({\theta }_0\right)}^{-1}{U}_{n\tau }\left({\theta }_0\right)\Vert :\tau \in N\left(ϵ\right)\right]\right\}\to 0$ (26)

Proof

$\begin{array}{l}\left(\widehat{{\theta }_1}-\widehat{{\theta }_2}\right)-\frac{n}{\tau \left(n-\tau \right)}I{\left({\theta }_0\right)}^{-1}{U}_{n\tau }\left({\theta }_0\right)\\ =\left(\widehat{{\theta }_1}-{\theta }_0-\frac{1}{\tau }I{\left({\theta }_0\right)}^{-1}{U}_{1\tau }\left({\theta }_0\right)\right)-\left(\widehat{{\theta }_2}-{\theta }_0-\frac{1}{n-\tau }I{\left({\theta }_0\right)}^{-1}{U}_{\tau +1,n}\left({\theta }_0\right)\right)\\ \max {\tau }^{\frac{1}{2}}\left(\widehat{{\theta }_1}-\widehat{{\theta }_2}\right)-\frac{n}{\tau \left(n-\tau \right)}I{\left({\theta }_0\right)}^{-1}{U}_{n\tau }\left({\theta }_0\right)\\ \le \max {\tau }^{\frac{1}{2}}\left(\widehat{{\theta }_1}-{\theta }_0-\frac{1}{\tau }I{\left({\theta }_0\right)}^{-1}{U}_{1\tau }\left({\theta }_0\right)\right)\\ -\max {\tau }^{\frac{1}{2}}\left(\widehat{{\theta }_2}-{\theta }_0-\frac{1}{n-\tau }I{\left({\theta }_0\right)}^{-1}{U}_{\tau +1,n}\left({\theta }_0\right)\right)\end{array}$ (27)

Considering the term on the RHS, by theorem 3.3. For $\tau ,n\to \infty$

$\begin{array}{l}\max {\tau }^{\frac{1}{2}}\left(\widehat{{\theta }_1}-{\theta }_0-\frac{1}{\tau }I{\left({\theta }_0\right)}^{-1}{U}_{1\tau }\left({\theta }_0\right)\right)\to 0\\ \max {\tau }^{\frac{1}{2}}\left(\widehat{{\theta }_2}-{\theta }_0-\frac{1}{n-\tau }I{\left({\theta }_0\right)}^{-1}{U}_{\tau +1,n}\left({\theta }_0\right)\right)\to 0\end{array}$

Hence the proof.

Assume that within a finite set of data a change point τ exists and $n\to \infty$ such that $\tau ,\left(n-\tau \right)\to \infty$

Define,

$U_{n\tau }\left({\theta }_0\right)=U_{1\tau }\left({\theta }_0\right)-\frac{\tau }{n}{U}_{1n}(\; \theta \; 0\; )$

Consider the following two sample homogeneity test

$Q_{n\tau }=\frac{n}{\tau \left(n-\tau \right)}{U}_{n\tau }\left({\theta }_0\right)I\left({\theta }_0\right)U_{n\tau }\left({\theta }_0\right)\text{for}1<\tau <n$ (28)

[15] defined a consistent estimate of 28 as

$\widehat{Q_{n\tau }}=\frac{n}{\tau \left(n-\tau \right)}{U}_{\tau }\left(\widehat{{\theta }_n}\right){\left(H_n\left(\widehat{{\theta }_n}\right)\right)}^{-1}{U}_{\tau }\left(\widehat{{\theta }_n}\right)$ (29)

By the principles of maximum likelihood estimation, $Q_{nn}=0$ since $U_n\left(\widehat{{\theta }_n}\right)=0$, $Q_{n0}=0$ since $U_0(.)=0$.

Consider $U_{\tau }\left(\widehat{{\theta }_n}\right)$. By Taylor’s theorem,

$\begin{array}{l}{U}_{\tau }\left(\widehat{{\theta }_n}\right)=U_{\tau }\left({\theta }_{\tau }\right)+\left(\widehat{{\theta }_n}-\widehat{{\theta }_{\tau }}\right){U^{\prime }}_{\tau }\left({\theta }_{\tau }\right)\\ {U^{\prime }}_{\tau }\left({\theta }_{\tau }\right)=\underset{i=1}{\overset{\tau }{{\displaystyle \sum }}}\frac{{\partial }^2}{\partial {\theta }_{\tau }^2}\log f\left(x;{\theta }_{\tau }\right)\\ =\left(\widehat{{\theta }_n}-\widehat{{\theta }_{\tau }}\right)\underset{i=1}{\overset{\tau }{{\displaystyle \sum }}}\frac{{\partial }^2}{\partial {\theta }_{\tau }^2}\log f\left(x;{\theta }_{\tau }\right)\\ =\tau H_{\tau }\left(\widehat{{\theta }_{\tau }}\right)\left(\widehat{{\theta }_n}-\widehat{{\theta }_{\tau }}\right)\end{array}$ (30)

Since by the principle of maximum likelihood estimation $U_{\tau }\left({\theta }_{\tau }\right)=0$.

$U_{\tau }\left(\widehat{{\theta }_n}\right)=-\tau H_{\tau }\left(\widehat{{\theta }_{\tau }}\right)\left(\widehat{{\theta }_{\tau }}-\widehat{{\theta }_n}\right)$ (31)

$\begin{array}{c}\left(\widehat{{\theta }_{\tau }}-\widehat{{\theta }_n}\right)=-\tau {\left\{H_{\tau }\left(\widehat{{\theta }_{\tau }}\right)\right\}}^{-1}{U}_{\tau }\left(\widehat{{\theta }_n}\right)\\ =-\tau {\left\{H_{\tau }\left(\widehat{{\theta }_{\tau }}\right)\right\}}^{-1}\left\{U_{1\tau }\left(\widehat{{\theta }_0}\right)-\frac{\tau }{n}{U}_{1n}\left(\widehat{{\theta }_0}\right)\right\}\\ =-\tau {\left\{H_{\tau }\left(\widehat{{\theta }_{\tau }}\right)\right\}}^{-1}\left\{\frac{1}{\tau }{U}_{1n}\left(\widehat{{\theta }_0}\right)-\frac{1}{n-\tau }{U}_{1n}\left(\widehat{{\theta }_0}\right)\right\}\\ =\tau {\left\{H_{\tau }\left(\widehat{{\theta }_{\tau }}\right)\right\}}^{-1}\left\{\frac{1}{n-\tau }{U}_{1n}\left(\widehat{{\theta }_0}\right)-\frac{1}{\tau }{U}_{1n}\left(\widehat{{\theta }_0}\right)\right\}\\ =-\frac{n\tau }{n-\tau }{\left\{H_{\tau }\left(\widehat{{\theta }_{\tau }}\right)\right\}}^{-1}{U}_{1n}\left(\widehat{{\theta }_0}\right)\\ =\frac{n\tau }{n-\tau }I\left(\stackrel{̂}{{\theta }_{\tau }}\right)U_{1n}\left(\widehat{{\theta }_0}\right)\end{array}$ (32)

By the CLT,

$\left(\widehat{{\theta }_{\tau }}-\widehat{{\theta }_n}\right)\to N\left(0,\frac{n-\tau }{n\tau }I{\left({\theta }_{\tau }\right)}^{-1}\right)$

and thus $\left(\widehat{{\theta }_{\tau }}-\widehat{{\theta }_n}\right)$ has squared Mahalanobis norm

$\left(\widehat{{\theta }_{\tau }}-\widehat{{\theta }_n}\right){\left(\frac{n-\tau }{n\tau }I{\left({\theta }_{\tau }\right)}^{-1}\right)}^{-1}\left(\widehat{{\theta }_{\tau }}-\widehat{{\theta }_n}\right)$ (33)

Hence

$\left(\widehat{{\theta }_{\tau }}-\widehat{{\theta }_n}\right){\left(\frac{n-\tau }{n\tau }I{\left({\theta }_{\tau }\right)}^{-1}\right)}^{-1}\left(\widehat{{\theta }_{\tau }}-\widehat{{\theta }_n}\right)\approx \widehat{Q_{n\tau }}$ (34)

implying that $Q_{n\tau }$ is approximately equal to the Mahalanobis norm of $\left(\widehat{{\theta }_{\tau }}-\widehat{{\theta }_n}\right)$. The Mahalanobis norm can be used to detect change points within a given finite time series data [11]. Since the test statistic 33 can quantify the difference between $\left(\widehat{{\theta }_n}\right)$ and $\left(\widehat{{\theta }_{\tau }}\right)$ then $\widehat{Q_{n\tau }}$ can similarly be used to quantify the deviation between the two parameter estimates. The value of $\widehat{Q_{n\tau }}$ ideally grows larger in evidence of the alternative hypothesis and tends towards zero when the null hypothesis is true. Suppose we define a maximal type test statistic $\widehat{Q_{n\tau }}\left(t\right)$ such that

$\widehat{Q_{n\tau }}=\max \left\{\widehat{Q_{n\tau }}\left(t\right):t\in N\left(ϵ\right)\right\}$ (35)

then we can obtain a measure of the largest difference between $\left(\widehat{{\theta }_n}\right)$ and $\left(\widehat{{\theta }_{\tau }}\right)$. Consider the divergence based estimator which was reduced to a two sample test statistic in Equation (11).

Definition 3.1. A matrix M is called positive definite if $x^{\prime }Mx\ge 0,\forall x\in R^n$, with equality if and only if $x=0$. The following inequality holds,

$\Vert x^{\prime }Mx-y^{\prime }My\Vert \le \left|M\right|\left\{{\Vert x-y\Vert }^2+2\Vert y\Vert \Vert x-y\Vert \right\}$ (36)

Consider the following result

$\begin{array}{l}\left|W_{n\tau }-Q_{n\tau }\right|=|\frac{\tau \left(n-\tau \right)}{n}\left(\widehat{{\theta }_1}-\widehat{{\theta }_2}\right)I\left({\theta }_0\right)\left(\widehat{{\theta }_1}-\widehat{{\theta }_2}\right)\begin{array}{c}\underset{}{\overset{}{}}\\ \end{array}\\ -{\left\{\frac{n}{\tau \left(n-\tau \right)}I{\left({\theta }_0\right)}^{-1}{U}_{n\tau }\left({\theta }_0\right)\right\}}^{\prime }I\left({\theta }_0\right)\left\{\frac{n}{\tau \left(n-\tau \right)}I{\left({\theta }_0\right)}^{-1}{U}_{n\tau }\left({\theta }_0\right)\right\}|\end{array}$ (37)

By inequality 36

$\begin{array}{l}\left|W_{n\tau }-Q_{n\tau }\right|<\left|I\left({\theta }_0\right)\right|\{{\Vert \left(\widehat{{\theta }_1}-\widehat{{\theta }_2}\right)-\frac{n}{\tau \left(n-\tau \right)}I{\left({\theta }_0\right)}^{-1}{U}_{n\tau }\left({\theta }_0\right)\Vert }^2\\ +2\Vert \frac{n}{\tau \left(n-\tau \right)}I{\left({\theta }_0\right)}^{-1}{U}_{n\tau }\left({\theta }_0\right)\Vert \Vert \left(\widehat{{\theta }_1}-\widehat{{\theta }_2}\right)-\frac{n}{\tau \left(n-\tau \right)}I{\left({\theta }_0\right)}^{-1}{U}_{n\tau }\left({\theta }_0\right)\Vert \}\end{array}$ (38)

Consider the last term on the RHS. By the result of theorem 3.4

$\Vert \left(\widehat{{\theta }_1}-\widehat{{\theta }_2}\right)-\frac{n}{\tau \left(n-\tau \right)}I{\left({\theta }_0\right)}^{-1}{U}_{n\tau }\left({\theta }_0\right)\Vert \to 0$ (39)

And hence

${\Vert \left(\widehat{{\theta }_1}-\widehat{{\theta }_2}\right)-\frac{n}{\tau \left(n-\tau \right)}I{\left({\theta }_0\right)}^{-1}{U}_{n\tau }\left({\theta }_0\right)\Vert }^2\to 0$ (40)

Considering the second term on the RHS. By the results in theorem 3.2,

$\Vert I{\left({\theta }_0\right)}^{-1}{U}_{n\tau }\left({\theta }_0\right)\Vert =O_p\left(1\right)$ (41)

From these results as $\tau ,n\to \infty$

$\left|W_{n\tau }-Q_{n\tau }\right|\to 0$ (42)

Definition 3.2. (Asymptotic consistency). A change point detection algorithm is said to be asymptotically consistent if the estimated segmentation is such that

$\max \left|\frac{\hat{\tau }}{n}-\frac{\tau }{n}\right|\to 0$ (43)

The change point fractions are consistent, and not the indexes themselves. Consistency results in the literature only deal with change point fractions since the distances $\left|\hat{\tau }-\tau \right|$ and their estimated counter parts do not converge to zero [11].

4. Change Point Analysis in the Generalized Pareto Distribution

Definition 4.1. The Generalized Pareto distribution function is defined by;

$H\left(x\right)=\{\begin{array}{l}1-{\left(1+\frac{\xi x}{\sigma }\right)}^{-\frac{1}{\xi }},\xi \ne 0\\ 1-\exp \left(-\frac{x}{\sigma }\right),\xi =0\end{array}$ (44)

where,

$x\in \{\begin{array}{l}\left[0,\infty \right),\xi \ge 0\\ \left[0,-\frac{\sigma }{\xi }\right],\xi <0\end{array}$

σ is referred to as the scale parameter characterizes the spread of the distribution and ξ referred to as the tail index/shape parameter determines the tail thickness. More specifically, given that $X\sim GP\left(\sigma ,\xi \right)$ then the probability density function is;

$h\left(x\right)=\{\begin{array}{l}\frac{1}{\sigma }{\left(1+\frac{\xi x}{\sigma }\right)}^{-\frac{1}{\xi }-1},\xi \ne 0\\ \frac{1}{\sigma }\exp \left(-\frac{x}{\sigma }\right),\xi =0\end{array}$ (45)

For any given finite set of data, at least one of the following is likely at any given change point $\tau \left(1<\tau <n\right)$ : ξ changes by a non-zero quantity; σ changes by a non-zero quantity; both ξ and σ change by non-zero quantities. A simple change point problem can be formulated in one of the following ways;

$\begin{array}{l}{H}_0:X_t~GP\left({\sigma }_1,{\xi }_1\right)\text{against}\\ H_1:X_t~GP\left({\sigma }_1,{\xi }_1\right)t\le \tau \\ X_t~GP\left({\sigma }_2,{\xi }_2\right)t>\tau \end{array}$ (46)

$\begin{array}{l}{H}_0:X_t~GP\left({\sigma }_1,{\xi }_1\right)\text{against}\\ H_1:X_t~GP\left({\sigma }_1,{\xi }_1\right)t\le \tau \\ X_t~GP\left({\sigma }_1,{\xi }_2\right)t>\tau \end{array}$ (47)

$\begin{array}{l}{H}_0:X_t~GP\left({\sigma }_1,{\xi }_1\right)\text{against}\\ H_1:X_t~GP\left({\sigma }_1,{\xi }_1\right)t\le \tau \\ X_t~GP\left({\sigma }_2,{\xi }_1\right)t>\tau \end{array}$ (48)

Since change points are unknown in advance, then either of the three hypothesis formulations is likely. Without knowledge on the types of changes contained in the time series, the question arises on which testing procedure to use. In most instances hypotheses 46 is tested since it is assumed that both distributional parameters change.

Figure 1 shows different GP density plots with a constant scale parameter but varying shape parameters. On the other hand, Figure 2 shows different GP density plots with a both scale and shape parameters varying. If any of the parameters were to change at any given point in time, then the thickness of the general tail distribution would change and this would in turn have an effect of the intensity of extreme values observed.

Assume that X is independently and identically distributed random variables drawn for the generalized Pareto distribution and consider a sample data set $x_1,\cdots ,x_{\tau },x_{\tau +1},\cdots ,x_n$ of fixed size n(n ≥ 3). Say $f_{{\theta }_1}$ is governed by the parameter space ${\theta }_1=\left({\xi }_1,{\sigma }_1\right)$ and $f_{{\theta }_2}$ is governed by the parameter space ${\theta }_2=\left({\xi }_2,{\sigma }_2\right)$ where ${\theta }_1\ne {\theta }_2\in \Theta$. The data set is assumed to contain an unknown change point τ where the distribution parameters ξ and σ abruptly change. Then

$\begin{array}{l}{x}_1,\cdots ,x_{\tau }~f_{{\theta }_1}\left(x\right)\\ x_{\tau +1},\cdots ,x_n~f_{{\theta }_2}(\; x\; )\end{array}$

Then the density function 49 governs the first τ observations and 50 governs the last $\left(n-\tau \right)$ observations.

Figure 1. Density plot with constant scale.

Figure 2. Density plot with varying scale and shape.

$f_{{\theta }_1}\left(x\right)=\{\begin{array}{l}\frac{1}{{\sigma }_1}{\left(1+\frac{{\xi }_{1}x}{{\sigma }_1}\right)}^{-\frac{1}{{\xi }_1}-1},{\xi }_1\ne 0\\ \frac{1}{{\sigma }_1}\exp \left(-\frac{x}{{\sigma }_1}\right),{\xi }_1=0\end{array}$ (49)

$f_{{\theta }_2}\left(x\right)=\{\begin{array}{l}\frac{1}{{\sigma }_2}{\left(1+\frac{{\xi }_{2}x}{{\sigma }_2}\right)}^{-\frac{1}{{\xi }_2}-1},{\xi }_1\ne 0\\ \frac{1}{{\sigma }_2}\exp \left(-\frac{x}{{\sigma }_2}\right),{\xi }_1=0\end{array}$ (50)

We will restrict to the case where $\xi >0$ i.e. heavy tailed distributions thereby only considering the first part of the density function with support $x\in \left[0,\infty \right)$.

From the divergence in Equation (5), let $\varphi \left(t\right)=-\log (\; t\; )$

$\begin{array}{c}{D}_{\varphi }\left({\theta }_1,{\theta }_2\right)={\displaystyle \int f_{{\theta }_2}\left(x\right)\varphi \left(\frac{f_{{\theta }_1}\left(x\right)}{f_{{\theta }_2}\left(x\right)}\right)\text{d}\mu \left(x\right)}\\ ={\displaystyle \int f_{{\theta }_2}\left(x\right)-\log \left(\frac{f_{{\theta }_1}\left(x\right)}{f_{{\theta }_2}\left(x\right)}\right)\text{d}\mu \left(x\right)}\\ ={\displaystyle \int f_{{\theta }_2}\left(x\right)\log \left(\frac{f_{{\theta }_2}\left(x\right)}{f_{{\theta }_1}\left(x\right)}\right)\text{d}\mu \left(x\right)}\\ =D_{KL}\left(f_{{\theta }_2}\left(x\right),f_{{\theta }_1}\left(x\right)\right)\equiv D_{KL}\left({\theta }_2,{\theta }_1\right)\end{array}$ (51)

An application of properties of the generalized Pareto distribution [16], numerical computations and methods of integration the divergence between two generalized Pareto distributions becomes

$\begin{array}{c}{D}_{KL}\left({\theta }_2,{\theta }_1\right)=\log \left(\frac{{\sigma }_2}{{\sigma }_1}\right)-\left(1+{\xi }_1\right)\\ -\left(\frac{1}{{\xi }_2}+1\right)\frac{{\sigma }_1}{{\sigma }_2}{\xi }_1{{\displaystyle \int }}^{\text{}}{\left(1+\frac{{\xi }_1}{{\sigma }_1}x\right)}^{-\frac{1}{{\xi }_1}}{\left(\frac{{\xi }_2}{{\sigma }_2}+1\right)}^{-1}\text{d}x\end{array}$ (52)

The divergence is a function of the parameters of the two densities.

5. Simulation Study

The performance of the estimator is examined by considering the effects of the change in sample size. The single change-point estimation problem is considered where the change-point τ is fixed at n/2 for n = 200, 500, 1000. Figures 3-5 display the plots for the location of the change-point estimator as estimated by the proposed estimator 10 with the divergence measure as in 52 for the various sample sizes. The hypothesis considered here is

$\begin{array}{l}{H}_0:X_t~GP\left(1,0.1\right)\text{against}\\ H_1:X_t~GP\left(1,0.1\right)t\le \tau \\ X_t~GP\left(3,0.35\right)t>\tau \end{array}$ (53)

Figure 3. Sample size= 200, $\tau =100$, $\hat{\tau }=88$.

Figure 4. Sample size= 500, $\tau =250$, $\hat{\tau }=245$.

Figure 5. Sample size= 1000, $\tau =500$, $\hat{\tau }=494$.

To check consistency of the estimator, we consider the following: first, we consider data simulated from the GP density with parameters $\left(1,{\xi }_1\right)$ and $\left(3,{\xi }_2\right)$ for the scale and shape respectively before and after the change point. 1000 simulations are carried out to estimate the change point and the results are given in Table 1 and Table 2.

6. Conclusion

In this paper, a divergence (pseudo-distance) based estimator is used to detect change points within a parametric framework focusing on the generalized Pareto

Table 1. Effect of the sample size with varying scale and varying shape ( $\tau =n/2$ ).

Table 2. Effect of the sample size with varying scale and varying shape ( $\tau =n/3$ ).

distribution. Change points are attributed to the change in model parameters at unknown points in time with the parameter estimates before and after the change point unknown. The estimator is shown to be consistent theoretically. Simulation studies also show that the change point estimator is consistent.

Acknowledgements

The first author thanks the Pan-African University Institute of Basic Sciences, Technology and Innovation (PAUSTI) for funding this research.

Appendix

Derivation of the change point estimator $W_{n\tau }$

Consider a second order Taylor expansion of $D_{\varphi }\left(\widehat{{\theta }_1},\widehat{{\theta }_2}\right)$ about the true parameter values ${\theta }_1,{\theta }_2$

For $i=1,\cdots ,d$

$\begin{array}{c}{D}_{\varphi }\left(\widehat{{\theta }_1},\widehat{{\theta }_2}\right)=D_{\varphi }\left({\theta }_1,{\theta }_2\right)+\underset{i=1}{\overset{d}{{\displaystyle \sum }}}\frac{\partial D_{\varphi }\left({\theta }_1,{\theta }_2\right)}{\partial {\theta }_{1i}}\left(\widehat{{\theta }_{1i}}-{\theta }_{1i}\right)\\ +\underset{i=1}{\overset{d}{{\displaystyle \sum }}}\frac{\partial D_{\varphi }\left({\theta }_1,{\theta }_2\right)}{\partial {\theta }_{1i}}\left(\widehat{{\theta }_{1i}}-{\theta }_{1i}\right)\\ +\frac{1}{2}\underset{i=1}{\overset{d}{{\displaystyle \sum }}}\underset{i=1}{\overset{d}{{\displaystyle \sum }}}\frac{{\partial }^2{D}_{\varphi }\left({\theta }_1,{\theta }_2\right)}{\partial {\theta }_{1i}\partial {\theta }_{1j}}{\left(\widehat{{\theta }_{1i}}-{\theta }_{1i}\right)}^{\prime }\left(\widehat{{\theta }_{1i}}-{\theta }_{1i}\right)\\ +\frac{1}{2}\underset{i=1}{\overset{d}{{\displaystyle \sum }}}\underset{i=1}{\overset{d}{{\displaystyle \sum }}}\frac{{\partial }^2{D}_{\varphi }\left({\theta }_1,{\theta }_2\right)}{\partial {\theta }_{2i}\partial {\theta }_{2j}}{\left(\widehat{{\theta }_{2i}}-{\theta }_{2i}\right)}^{\prime }\left(\widehat{{\theta }_{2j}}-{\theta }_{2j}\right)\\ +\underset{i=1}{\overset{d}{{\displaystyle \sum }}}\underset{i=1}{\overset{d}{{\displaystyle \sum }}}\frac{{\partial }^2{D}_{\varphi }\left({\theta }_1,{\theta }_2\right)}{\partial {\theta }_{1i}\partial {\theta }_{2j}}{\left(\widehat{{\theta }_{1i}}-{\theta }_{1i}\right)}^{\prime }\left(\widehat{{\theta }_{2j}}-{\theta }_{2j}\right)\\ +o\left({\Vert \widehat{{\theta }_1}-{\theta }_1\Vert }^2\right)+o\left({\Vert \widehat{{\theta }_2}-{\theta }_2\Vert }^2\right)\end{array}$ (54)

Under the assumption of the null hypothesis,

$\begin{array}{c}\frac{\partial D_{\varphi }\left({\theta }_1,{\theta }_2\right)}{\partial {\theta }_{1i}}={\displaystyle \int {\varphi }^{\prime }\left(\frac{f_{{\theta }_1}\left(x\right)}{f_{{\theta }_2}\left(x\right)}\right)\frac{\partial f_{{\theta }_1}\left(x\right)}{\partial {\theta }_{1i}}\text{d}\mu \left(x\right)}\\ ={\varphi }^{\prime }\left(1\right){\displaystyle \int \frac{\partial f_{{\theta }_1}\left(x\right)}{\partial {\theta }_{1i}}\text{d}\mu \left(x\right)}\\ ={\varphi }^{\prime }\left(1\right)\frac{\partial }{\partial {\theta }_{1i}}{\displaystyle \int f_{{\theta }_1}\left(x\right)\text{d}\mu \left(x\right)}\\ =0\end{array}$ (55)

This is by assumption 1 and that interchanges of derivatives and integrals are valid.

$\begin{array}{l}\frac{{\partial }^2{D}_{\varphi }\left({\theta }_1,{\theta }_2\right)}{\partial {\theta }_{1i}\partial {\theta }_{1j}}={{\displaystyle \int }}^{\text{}}\frac{\partial f_{{\theta }_1}(x)}{\partial {\theta }_{1i}}{\varphi }^{″}\left(\frac{f_{{\theta }_1}\left(x\right)}{f_{{\theta }_2}\left(x\right)}\right)\frac{\partial f_{{\theta }_1}\left(x\right)}{\partial {\theta }_{1j}}\frac{1}{f_{{\theta }_2}\left(x\right)}\text{d}\mu \left(x\right)\\ ={\varphi }^{″}\left(1\right){{\displaystyle \int }}^{\text{}}\frac{\partial f_{{\theta }_1}\left(x\right)}{\partial {\theta }_{1i}}\frac{\partial f_{{\theta }_1}\left(x\right)}{\partial {\theta }_{1j}}\frac{1}{f_{{\theta }_1}\left(x\right)}\text{d}\mu \left(x\right)\\ ={{\displaystyle \int }}^{\text{}}\frac{\partial f_{{\theta }_1}\left(x\right)}{\partial {\theta }_{1i}}\frac{\partial f_{{\theta }_1}\left(x\right)}{\partial {\theta }_{1j}}\frac{1}{f_{{\theta }_1}\left(x\right)}\text{d}\mu (\; x\; )\end{array}$

$\begin{array}{l}\frac{{\partial }^2{D}_{\varphi }\left({\theta }_1,{\theta }_2\right)}{\partial {\theta }_{2i}\partial {\theta }_{2j}}={\displaystyle \int {\varphi }^{″}}\left(\frac{f_{{\theta }_2}(x)}{f_{{\theta }_1}(x)}\right)\frac{\partial f_{{\theta }_2}\left(x\right)}{\partial {\theta }_{2i}}\frac{\partial f_{{\theta }_2}\left(x\right)}{\partial {\theta }_{2j}}\frac{1}{f_{{\theta }_1}\left(x\right)}\text{d}\mu \left(x\right)\\ ={\varphi }^{″}\left(1\right){{\displaystyle \int }}^{\text{}}\frac{\partial f_{{\theta }_2}\left(x\right)}{\partial {\theta }_{2i}}\frac{\partial f_{{\theta }_2}\left(x\right)}{\partial {\theta }_{2j}}\frac{1}{f_{{\theta }_1}\left(x\right)}\text{d}\mu \left(x\right)\\ ={\varphi }^{″}\left(1\right){{\displaystyle \int }}^{\text{}}\frac{\partial f_{{\theta }_2}\left(x\right)}{\partial {\theta }_{2i}}\frac{\partial f_{{\theta }_2}\left(x\right)}{\partial {\theta }_{2j}}\frac{1}{f_{{\theta }_1}\left(x\right)}\text{d}\mu \left(x\right)\end{array}$ (56)

$\begin{array}{l}\frac{{\partial }^2{D}_{\varphi }\left({\theta }_1,{\theta }_2\right)}{\partial {\theta }_{1i}\partial {\theta }_{2j}}={\displaystyle \int {\varphi }^{″}}\left(\frac{f_{{\theta }_1}\left(x\right)}{f_{{\theta }_2}\left(x\right)}\right)\frac{\partial f_{{\theta }_1}\left(x\right)}{\partial {\theta }_{1i}}\frac{\partial f_{{\theta }_2}\left(x\right)}{\partial {\theta }_{2j}}-\frac{1}{{\left(f_{{\theta }_2}\left(x\right)\right)}^2}{f}_{{\theta }_1}\left(x\right)\text{d}\mu \left(x\right)\\ =-{\varphi }^{″}\left(1\right){{\displaystyle \int }}^{\text{}}\frac{\partial f_{{\theta }_1}\left(x\right)}{\partial {\theta }_{1i}}\frac{\partial f_{{\theta }_2}\left(x\right)}{\partial {\theta }_{2j}}\frac{1}{f_{{\theta }_1}\left(x\right)}\text{d}\mu \left(x\right)\\ =-\left\{\frac{{\partial }^2{D}_{\varphi }\left({\theta }_1,{\theta }_2\right)}{\partial {\theta }_{1i}\partial {\theta }_{1j}}\right\}\end{array}$

By the standard regularity assumptions (theorem 5.2.1) [14], then

$\begin{array}{l}\frac{{\partial }^2{D}_{\varphi }\left({\theta }_1,{\theta }_2\right)}{\partial {\theta }_{1i}\partial {\theta }_{1j}}=\frac{{\partial }^2{D}_{\varphi }\left({\theta }_1,{\theta }_2\right)}{\partial {\theta }_{2i}\partial {\theta }_{2j}}=I\left(\theta \right)\\ \frac{{\partial }^2{D}_{\varphi }\left({\theta }_1,{\theta }_2\right)}{\partial {\theta }_{1i}\partial {\theta }_{2j}}=-I\left(\theta \right)\end{array}$ (57)

Using the arguments in (55)-(57) Equation (54) reduces to

$\begin{array}{l}\frac{1}{2}{\left(\widehat{{\theta }_1}-{\theta }_1\right)}^{\prime }I\left({\theta }_1\right)\left(\widehat{{\theta }_1}-{\theta }_1\right)+\frac{1}{2}{\left(\widehat{{\theta }_2}-{\theta }_1\right)}^{\prime }I\left({\theta }_1\right)\left(\widehat{{\theta }_2}-{\theta }_1\right)\\ -{\left(\widehat{{\theta }_1}-{\theta }_1\right)}^{\prime }I\left({\theta }_1\right)\left(\widehat{{\theta }_2}-{\theta }_2\right)+o\left({\Vert \widehat{{\theta }_1}-{\theta }_1\Vert }^2\right)+o\left({\Vert \widehat{{\theta }_2}-{\theta }_2\Vert }^2\right)\end{array}$ (58)

Further,

$\frac{2}{{\varphi }^{″}\left(1\right)}{D}_{\varphi }\left(\widehat{{\theta }_1},\widehat{{\theta }_2}\right)={\left(\widehat{{\theta }_1}-{\theta }_2\right)}^{\prime }I\left({\theta }_1\right)\left(\widehat{{\theta }_1}-{\theta }_2\right)+o\left({\Vert \widehat{{\theta }_1}-{\theta }_1\Vert }^2\right)+o\left({\Vert \widehat{{\theta }_2}-{\theta }_2\Vert }^2\right)$ (59)

Assuming that a change point τ divides the data into two heterogeneous parts with the parameters ${\theta }_1,{\theta }_2$ before and after the change point respectively with sample sizes τ, (n − τ) respectively, then by the regularity conditions the mles’s are such that

$\begin{array}{l}\sqrt{\tau }\left(\widehat{{\theta }_1}-{\theta }_1\right)\to N\left(0,I{\left({\theta }_1\right)}^{-1}\right)\\ \sqrt{n-\tau }\left(\widehat{{\theta }_2}-{\theta }_2\right)\to N\left(0,I{\left({\theta }_2\right)}^{-1}\right)\end{array}$ (60)

For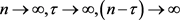

Let 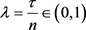then,

$\begin{array}{l}\sqrt{\frac{\tau \left(n-\tau \right)}{n}}\left(\widehat{{\theta }_1}-{\theta }_1\right)\to N\left(0,\lambda I{\left({\theta }_1\right)}^{-1}\right)\\ \sqrt{\frac{\tau \left(n-\tau \right)}{n}}\left(\widehat{{\theta }_2}-{\theta }_2\right)\to N\left(0,\left(1-\lambda \right)I{\left({\theta }_2\right)}^{-1}\right)\end{array}$ (61)

By the assumption of the null hypothesis ${\theta }_1={\theta }_2={\theta }_0$,

$\sqrt{\frac{\tau \left(n-\tau \right)}{n}}\left(\widehat{{\theta }_2}-\widehat{{\theta }_1}\right)\to N\left(0,I{\left({\theta }_0\right)}^{-1}\right)$ (62)

under the assumption that the parameter estimates are consistent.

Suppose that under the maximum likelihood estimation for a sample of fixed size n, $\widehat{{\theta }_n}\to \theta$ as $n\to \infty$. By the law of large numbers, the observed information matrix is such that,

$I_n\left(\theta \right)=\left[\frac{1}{n}\underset{i=1}{\overset{n}{{\displaystyle \sum }}}-\frac{{\partial }^2}{\partial {\theta }_i\partial {\theta }_j}\log f\left(x;\theta \right)\right]\to \left[E\left(-\frac{{\partial }^2}{\partial {\theta }_i\partial {\theta }_j}\log f\left(x;\theta \right)\right)\right]=I\left(\theta \right)$ (63)

If we substitute $\widehat{{\theta }_n}$ for $\theta$

$I_n\left(\theta \right)={\left[\frac{1}{n}\underset{i=1}{\overset{n}{{\displaystyle \sum }}}-\frac{{\partial }^2}{\partial {\theta }_i\partial {\theta }_j}\log f\left(x;\theta \right)\right]}_{\theta ={\theta }_n}\to \left[E\left(-\frac{{\partial }^2}{\partial {\theta }_i\partial {\theta }_j}\log f\left(x;\theta \right)\right)\right]=I\left(\theta \right)$ (64)

which is defined as a consistent estimator of the information matrix.

The elements of $I\left(\theta \right)$ are continuous in $\theta$ and it holds that

$I_n\left(\theta \right)\to I\left(\theta \right)\text{as}n\to \infty$ (65)

From Equation (59) we obtain

$\frac{\tau \left(n-\tau \right)}{n}{\left(\widehat{{\theta }_1}-{\theta }_2\right)}^{\prime }I\left({\theta }_1\right)\left(\widehat{{\theta }_1}-{\theta }_2\right)+o\left({\Vert \widehat{{\theta }_1}-{\theta }_1\Vert }^2\right)+o\left({\Vert \widehat{{\theta }_2}-{\theta }_2\Vert }^2\right)$ (66)

From Equation (9) and Equations (56)-(66) then the test statistic can be expressed as

$D_{n\tau }=\underset{\tau \in N\left(ϵ\right)}{\max }\frac{\tau \left(n-\tau \right)}{n}\left\{{\left(\widehat{{\theta }_1}-{\theta }_2\right)}^{\prime }I\left({\theta }_1\right)\left(\widehat{{\theta }_1}-{\theta }_2\right)+o\left({\Vert \widehat{{\theta }_1}-{\theta }_1\Vert }^2\right)+o\left({\Vert \widehat{{\theta }_2}-{\theta }_2\Vert }^2\right)\right\}$ (67)

Let

$\begin{array}{l}\underset{\tau \in N\left(ϵ\right)}{\max }\frac{\tau \left(n-\tau \right)}{n}\left\{\stackrel{^}{{\left(\widehat{{\theta }_1}-{\theta }_2\right)}^{\prime }}\widehat{I\left({\theta }_1\right)}\left(\widehat{{\theta }_1}-{\theta }_2\right)\right\}=W_{n\tau }\\ \underset{\tau \in N\left(ϵ\right)}{\max }{D}_{n\tau }=\underset{\tau \in N\left(ϵ\right)}{\max }{W}_{n\tau }+o\left({\Vert \widehat{{\theta }_1}-{\theta }_1\Vert }^2\right)+o\left({\Vert \widehat{{\theta }_2}-{\theta }_2\Vert }^2\right)\end{array}$ (68)

But

$\begin{array}{l}o\left({\Vert \widehat{{\theta }_1}-{\theta }_1\Vert }^2\right)=o_p\left(1\right)\\ o\left({\Vert \widehat{{\theta }_2}-{\theta }_2\Vert }^2\right)=o_p(\; 1\; )\end{array}$

Since the second and third terms of 67 are $o_p\left(1\right)$ then the distribution of $D_{n\tau }$ is similar to that of $W_{n\tau }$.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Brodsky, E. and Darkhovsky, B.S. (2013) Nonparametric Methods in Change Point Problems. Vol. 243, Springer Science & Business Media, Berlin.
[2]	Killick, R. and Eckley, I. (2014) Change Point: An R Package for Change Point Analysis. Journal of Statistical Software, 58, 1-19. https://doi.org/10.18637/jss.v058.i03
[3]	Korkas, K.K. and Fryzlewicz, P. (2017) Multiple Change-Point Detection for Non-Stationary Time Series Using Wild Binary Segmentation. Statistica Sinica, 27, 287-311. https://doi.org/10.5705/ss.202015.0262
[4]	Csorgo, M. and Horváth, L. (1997) Limit Theorems in Change-Point Analysis. Vol. 18, John Wiley & Sons Inc., Hoboken.
[5]	Page, E. (1955) A Test for a Change in a Parameter Occurring at an Unknown Point. Biometrika, 42, 523-527. https://doi.org/10.1093/biomet/42.3-4.523
[6]	Cheng, L., AghaKouchak, A., Gilleland, E. and Katz, R.W. (2014) Non-Stationary Extreme Value Analysis in a Changing Climate. Climatic Change, 127, 353-369. https://doi.org/10.1007/s10584-014-1254-5
[7]	Jarusková, D. and Rencová, M. (2008) Analysis of Annual Maximal and Minimal Temperatures for Some European Cities by Change Point Methods. Environmetrics, 19, 221-233. https://doi.org/10.1002/env.865
[8]	Naveau, P., Guillou, A. and Rietsch, T. (2014) A Non-Parametric Entropy-Based Approach to Detect Changes in Climate Extremes. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 76, 861-884. https://doi.org/10.1111/rssb.12058
[9]	Dupuis, D., Sun, Y. and Wang, H.J. (2015) Detecting Change-Points in Extremes. Statistics and Its Interface, 8, 19-31. https://doi.org/10.4310/SII.2015.v8.n1.a3
[10]	Dette, H. and Wu, W. (2018) Change Point Analysis in Non-Stationary Processes: A Mass Excess Approach.
[11]	Truong, C., Oudre, L. and Vayatis, N. (2018) A Review of Change Point Detection Methods.
[12]	Pardo, L. (2018) Statistical Inference Based on Divergence Measures. Chapman and Hall/CRC, London. https://doi.org/10.1201/9781420034813
[13]	Andrews, D.W. (1993) Tests for Parameter Instability and Structural Change with Unknown Change Point. Econometrica: Journal of the Econometric Society, 61, 821-856. https://doi.org/10.2307/2951764
[14]	Sen, P.K. and Singer, J.M. (2017) Large Sample Methods in Statistics (1994): An Introduction with Applications. CRC Press, Boca Raton. https://doi.org/10.1201/9780203711606
[15]	Hawkins Jr., D.L. (1983) Sequential Detection Procedures for Autoregressive Processes. Dept. of Statistics, Tech. Rep., North Carolina State University, Raleigh.
[16]	Embrechts, P., Klüppelberg, C. and Mikosch, T. (2013) Modelling Extremal Events: For Insurance and Finance. Vol. 33, Springer Science & Business Media, Berlin.