Inference and Properties of Mixture Two Extreme Lower Bound Distributions ()
1. Introduction
Recently, the extreme value distribution is becoming increasingly important in engineering statistics as a suitable model to represent phenomena with usually large maximum observations. In engineering circles, this distribution is often called the extreme lower bound model. It is one of the pioneers of extreme value statistics. The extreme lower bound distribution is one of the probability distributions used to model extreme events. The generalization of the standard extreme lower bound distribution has been introduced by Nadarajah and Kotz [1] and Abd-Elfattah [2] . There are over fifty applications ranging from accelerated life testing through to earthquakes, floods, rain fall, queues in supermarkets, sea currents, wind speeds and track race records, see Kotz and Nadarajah [3] . Mixture models play an important role in many practical applications. For example, direct applications of finite mixture models are in fisheries research, economics, medicine, psychology, palaeoanthropology, botany, agriculture, zoology, life testing and reliability. Direct applications include outliers, Gaussian sums, cluster analysis, latent structure models, modeling prior densities, empirical Bayes method and nonparametric density estimation. In many applications, the available data can be considered as data coming from a mixture population of two or more distributions. This data enables us to mix statistical distributions to get a new distribution which has the properties of its components. For an excellent survey of estimation techniques, discussion and applications, mixture distribution have been considered extensively by many authors, see Titterington [4] , Maclachlan and Basford [5] , Lindsay [6] , Maclachlan and Krishnan [7] and Maclachlan and Peel [8] . Recently, there are many authors [4] [9] [10] who discuss the mixture models, Mohie El-Din et al. [11] [12] [13] . In this paper, we discuss some important measures of two extreme lower bound distributions. Also, we estimate the vector of unknown parameters of a mixture model via the EM algorithm proposed by Dempster et al. [9] . Further, we carry out some simulated illustrations using Monte Carlo method.
2. Description of the Model
The mixture of two extreme lower bound distributions has its pdf as
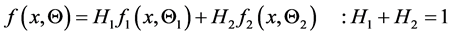(2.1)
where 
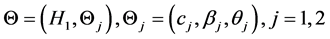and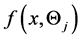
, the density func- tion of 
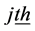component, is given by
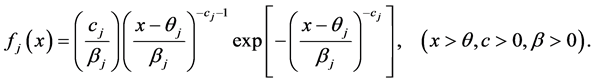(2.2)
The cdf of the mixture of two extreme lower bound distributions is given by
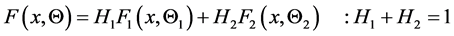(2.3)
where
, the cdf 
component, is given by
(2.4)
Such that, We study this case, when 
and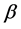 
are the parameters unknown and 
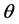is the parameter known.
3. Properties
In this section we obtain some properties for two extreme lower bound distri- bution by extending the corresponding results of the two parameters extreme lower bound distribution where (2.3)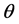 
is known as follow.
3.1. The Expected Value and Variance
The expected value of the pdf of the two extreme lower bound distribution obtain in (2.1) and (2.3) is
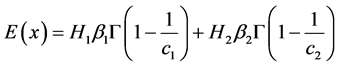(3.5)
and the variance is given by
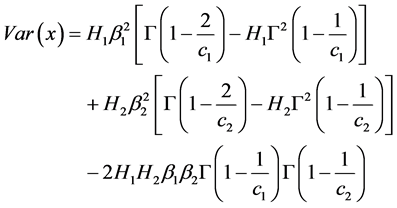(3.6)
3.2. Mode and Median
The mode of the mixture of two extreme lower bound distribution is obtained by solving the following nonlinear equation with respect to x
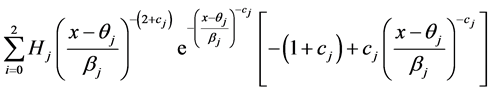(3.7)
By using (2.4) and (3.5), the median of the mixture of two extreme lower bound distribution is obtained by solving the following nonlinear equation with respect to x
(3.8)
From Table 1, we obtain the median and the mode of the mixture two extreme lower bound distribution based on different choices of the parameters 
and ![]()
for each ![]()
from this table we observe that the mode is slightly affected by the variation in the values of the mixing proportion![]()
, while one mode is stable in the bimodal case. In addition, for unimodal case, the median increases when ![]()
increases. From the bimodal case, we observe that the median decreases when ![]()
icreases.
3.3. Reliability and Failure Rate Function
The reliability function of the mixture two extreme lower bound distribution is given by
![]()
Table 1. The median and the mode of the mixture of two extreme lower bound distribution.
![]()
(3.9)
By using (2.4) and (3.5) it can be seen the failure rate function (hazard rate function) of the mixture two extreme lower bound distribution is given by
![]()
(3.10)
Which can be written as
![]()
(3.11)
where
![]()
and
![]()
The failure rate function of the mixture two extreme lower bound distribution given in (3. 10) satisfies the following limits
![]()
(3.12)
4. Estimation via EM Algorithm
The EM algorithm provides a simple computational method for fitting mixture models. We use the EM algorithm to estimate the parameters of the pdf of the mixture two extreme lower bound distribution which given in (2.1) and (2.3). We focus in this section, the Maximum likelihood fitting of two extreme lower bound distributions mixture via the EM algorithm. Maclachlan and Peel [9] , the essential nature of the algorithm is the alternation of expectation and maximization steps.
![]()
(4.13)
![]()
(4.14)
then, Concerning the E-step on the ![]()
iteration, the updated estimate of the ![]()
mixing proportion ![]()
is given by
![]()
(4.15)
From (4.13) we obtain the M-step of the ![]()
iteration, the updated estimates ![]()
and ![]()
for each ![]()
are obtained, respectively, by solving the following systems of equations
![]()
(4.16)
and
![]()
(4.17)
where
![]()
(4.18)
The estimates of ![]()
and ![]()
are obtained by solving (4.15), (4.17) and (4.18). Equations (4.15) and (4.17) are written explicitly but Equation (4.18) has to be solved numerically with random choices of the initial values.
5. Numerical Illustration
In order to calculate the estimates of the five parameters ![]()
and ![]()
where ![]()
and ![]()
are known that appear in the pdf of the mixture two extreme lower bound distribution given in (2.1) and (2.3) by using EM algorithm in a Monte Carlo simulation as follows:
Generate random sample of size ![]()
and 100 from the mixture two extreme lower bound distribution distribution with for each choice of the parameters ![]()
and![]()
. Some of choices caver the unimodal case and other caver the bimodal case.
The random samples of the mixtures are generated with respect to two uniform variables ![]()
and![]()
. If![]()
, then use ![]()
to generate a random variable x from the mixture two extreme lower bound distribution by using (3.5) as![]()
, but if![]()
, then![]()
.
The bias and the mean square errors of the estimates are calculated based on 10,000 Monte Carlo simulation and the results are illustrated in Table 2 and Table 3. We see that in most of the considered cases, the mean square errors of the estimated parameters decrease as n increase.
6. Conclusion
In this paper, the behaviors of the mode and median of the mixture two extreme
![]()
Table 2. Bais of the estimate of ![]()
based on EM algorithm.
![]()
Table 3. MSE of ![]()
based on EM algorithm.
lower bound distribution are investigated, based on different choices of the parameters. Also, the behaviors of the failure rate function are discussed through some different graphs. In addition, the estimation of the unknown parameters is obtained using the EM algorithm. Finally, a Monte Carlo simulation based on 10,000 runs is carried out.