1. Introduction
In this paper we shall use the terminology of [1]. Let 
be a simple graph with vertex set 
and edge set
. Let
,
. For every
, the open neighborhood of
, denoted by
, is a set 
and the closed neighborhood of
, denoted by
, is a set
. We write 
for the degree of a vertex 
and the maximum and minimum degree of 
are denoted by 
and
, respectively. For every
, the edge-closed neighborhood of
, denoted by
, is
.
Many domination parameters in graphs has been studied richly [2-4] A function 
is a signed dominating function if for every vertex
,
.
The weight 
of 
is the sum of the function values of all vertices in
. The signed domination number 
of 
is the minimum weight of signed dominating functions on
. This concept was introduced by Dunbar et al. [5] and has been studied by several authors [6-9]. As an extension of the signed domination, we give the definition of the reverse total signed vertex domination in a graph.
Definition 1. Let 
be a simple graph. A reverse total signed vertex dominating function of 
is a function 
such that 
for all
. The reverse total signed vertex domination number of
, denoted by
, is the maximum weight of a reverse total signed vertex dominating function of
. A reverse total signed vertex dominating function 
is called a 
-function of 
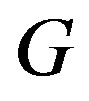if 
.
2. Properties of Reverse Total Signed Vertex Domination
Proposition 1 For any graph
,
.
Proof. Let 
be a 
-function of
. Then
.
Let
,
,
,
.
Then
.
Therefore
.
Propositon 2 For any graph
,
.
Proof. Let 
be a 
-function of
. Then for every
, 
and we have
Thus
.
Propositon 3 For any graph
,
.
Proof. Let 
be a 
-function of
.
, 
, 
and 
are defined as Proposition 2. Then
.
We define two induced graphs 
and 
of 
as follows:
, 
,
.
Then for every
,
and
. For every
, we have
and
. Thus
Therefore
Since
we have
. Therefore
.
Propositon 4 For any star
,
.
Proof. Let 
be a 
-function. Let
,
,
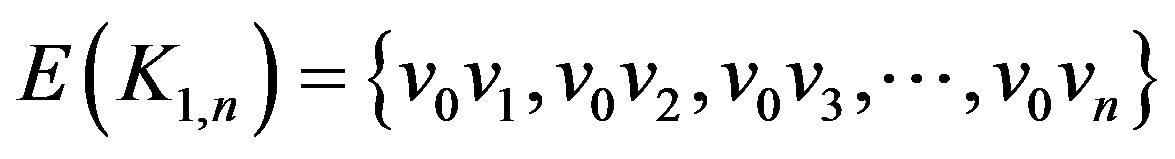where 
is the center of
. Since for every
, 
, we have
.
On the other hand, consider the function
such that
,
.
Then 
is a reverse total signed vertex dominating function on 
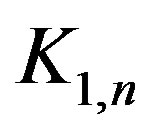and
.
Thus
, which implies that 
.
Propositon 5 For any circle
,
.
Proof. Let 
be a 
-function of
. Let
,
.
Since for every
,
, we have
.
Thus
.
Therefore
.
On the other hand, consider the mapping
such that
,
.
Then 
is a reverse total signed vertex dominating function on 
and
. Therefore
which implies
.
Propositon 6 For any complete bipartite graph
,
.
Proof. Let
be a 
-function. Let
, 
,
and
.
Since for every
,
, we have 
. Therefore
.
On the other hand, consider the mapping
such that
, 
for
,
for 
and
. Then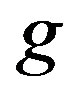 
is a reverse total signed vertex dominating function on 
and
. Therefore
which implies
.
3. Acknowledgements
This work was supported by the Natural Science Foundation of Hebei Province (A2012408002), the Educational Commission of Hebei Province (ZH2011122, Z2011157) and Langfang Teachers College (LSZQ201106).