1. Introduction
The connection between Number Theory and Dynamical Systems Theory is receiving recently a considerable attention. In this paper, we review some aspects of this connection focusing on the interplay between continued fractions and one dimensional dynamics. In Section 2, we review some known facts about fast and slow convergents, highlighting their relations both with irrational rotation dynamics and the ergodic theory of the Gauss map. In Section 3, after recalling the construction and the basic properties of the Farey tree, we describe different ways of coding the paths on it, as well as their dynamical counterparts obtained by combining fractional linear transformations. Deeper insights into these connections are provided by the Minkowski question mark function, whose properties are discussed in Section 4. Finally, in Section 5, we present some applications of the thermodynamical formalism based on the previous constructions.
2. Fast and Slow Convergents
We start by reviewing some well known facts about continued fractions1.
Let
 (2.1)
(2.1)
be the continued fraction expansion of the number . By applying Euclid’s algorithm one sees that the above expansion terminates if and only if x is a rational number. For x irrational one can construct recursively a sequence
. By applying Euclid’s algorithm one sees that the above expansion terminates if and only if x is a rational number. For x irrational one can construct recursively a sequence  of rational approximants of x as
of rational approximants of x as
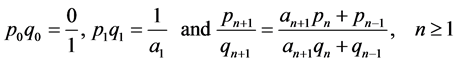 (2.2)
(2.2)
We can write this recursion in matrix form as follows: letting
 (2.3)
(2.3)
and noting that
 (2.4)
(2.4)
we have
 (2.5)
(2.5)
and
 (2.6)
(2.6)
A short manipulation of (2.2) gives . Since
. Since  one obtains inductively the Lagrange formula
one obtains inductively the Lagrange formula
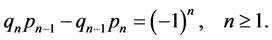 (2.7)
(2.7)
Another useful formula which can be easily obtained from (2.2) is the following: for all  and
and ,
,
 (2.8)
(2.8)
Letting  we get in particular
we get in particular
 (2.9)
(2.9)
Note that

and so forth. We thus have the so called mirror formula (some consequences of which have been investigated in [4] ):
 (2.10)
(2.10)
The numbers  are called continued fraction convergents (CFC) of x and it turns out that the n-th CFC
are called continued fraction convergents (CFC) of x and it turns out that the n-th CFC  is the best rational approximation to
is the best rational approximation to  whose denominator does not exceed
whose denominator does not exceed  [2] . One sees that
[2] . One sees that
 (2.11)
(2.11)
Putting 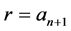 in (2.8) we get
in (2.8) we get
 (2.12)
(2.12)
But what happens if  in (2.8) takes on an intermediate value
in (2.8) takes on an intermediate value ?
?
Definition 2.1 For  the sets
the sets 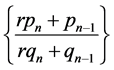 for
for  are the n’th Farey convergents (FC) for the real number
are the n’th Farey convergents (FC) for the real number .
.
Example. Let . The first five CFC are
. The first five CFC are

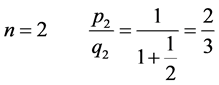



On the other hand, within the same accuracy, there are  FC’s. They are
FC’s. They are








We now need some notions.
Definition 2.2 The Farey sum over two rationals  and
and  is the mediant operation given by
is the mediant operation given by
 (2.13)
(2.13)
It is easy to see that  falls in the interval
falls in the interval  2. We say that
2. We say that  and
and  are Farey neighbours if
are Farey neighbours if
 . Two Farey neighbours define a Farey interval and each Farey interval can be labeled uniquely according to the mediant (child)
. Two Farey neighbours define a Farey interval and each Farey interval can be labeled uniquely according to the mediant (child)  of the neighbours.
of the neighbours.
Observe that given a pair of consecutive FC’s, say

for some  and
and , we have
, we have
 (2.14)
(2.14)
Moreover
 (2.15)
(2.15)
by Lagrange’s formula. Therefore, for every , each FC
, each FC  for
for 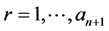 is a Farey neighbour of
is a Farey neighbour of
 , the corresponding Farey interval getting smaller and smaller as
, the corresponding Farey interval getting smaller and smaller as  increases. More precisely, using again Lagrange’s formula, one easily obtains
increases. More precisely, using again Lagrange’s formula, one easily obtains
 (2.16)
(2.16)
We therefore see that the FC  is the best one-sided rational approximation to
is the best one-sided rational approximation to  whose denominator does not exceed
whose denominator does not exceed  (although, if
(although, if , there might be a CFC with denominator less than
, there might be a CFC with denominator less than 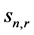 and closer to
and closer to 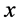 on the other side of x). Increasing r, once we arrive at
on the other side of x). Increasing r, once we arrive at  we hit a new CFC on the current side of
we hit a new CFC on the current side of , closer than the previous CFC. Finally, using matrix notation, the FC’s can be expressed in terms of intermediate products in (2.5) for
, closer than the previous CFC. Finally, using matrix notation, the FC’s can be expressed in terms of intermediate products in (2.5) for  as
as
 (2.17)
(2.17)
The algorithm which produces the sequence of  ‘s of a given real number is called slow continued fraction algorithm (see, e.g., [6] [7] ).
‘s of a given real number is called slow continued fraction algorithm (see, e.g., [6] [7] ).
Remark 2.3 The set  of Farey fractions of order
of Farey fractions of order  is the set of irreducible fractions in
is the set of irreducible fractions in  with denominator
with denominator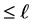 , listed in order of magnitude (see [8] ). Thus,
, listed in order of magnitude (see [8] ). Thus,  ,
,

and so on. In particular  with Euler totient function
with Euler totient function
 . Then we see that each
. Then we see that each  for
for  is consecutive to
is consecutive to  in
in 
for .
.
2.1. Connection to Rotations of the Circle
One can interpret the above construction in terms of a kind of renormalization procedure for rotations of the circle  through an angle
through an angle . With no loss we take the initial point to be the origin 0 and set
. With no loss we take the initial point to be the origin 0 and set .
.
Since  we have
we have 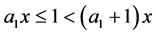 and thus
and thus

with
 (2.18)
(2.18)
Moreover we have

and therefore  or, which is the same,
or, which is the same,

with
 (2.19)
(2.19)
Iterating this procedure, we construct a family of nested intervals (see Figure 1) ,
,  , such that
, such that
 (2.20)
(2.20)
and
 (2.21)
(2.21)
where we have set . Using (2.18), (2.19) and (2.21) one gets inductively the formula
. Using (2.18), (2.19) and (2.21) one gets inductively the formula

Figure 1. The construction of nested intervals.
 (2.22)
(2.22)
Note that
 (2.23)
(2.23)
Now, if we denote by  the euclidean metric on
the euclidean metric on  then
then
 (2.24)
(2.24)
Therefore
 (2.25)
(2.25)
That is, the sequence of arc-lengths 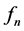 is but the sequence of successive closest distances to the initial point. This can be seen in the following way: starting from 0 and iterating
is but the sequence of successive closest distances to the initial point. This can be seen in the following way: starting from 0 and iterating  times one ends up at the point
times one ends up at the point  which lies on the left of 0 and is the point closest to 0 up to now, being distant
which lies on the left of 0 and is the point closest to 0 up to now, being distant  from it. Iterating
from it. Iterating  more times one ends up at the point
more times one ends up at the point  which lies on the left of 0 at distance
which lies on the left of 0 at distance , ... iterating
, ... iterating  times one ends up at the point
times one ends up at the point  which still lies on the left of 0, at distance
which still lies on the left of 0, at distance . One more iterate yields the point
. One more iterate yields the point  which now lies on the right of 0 at distance
which now lies on the right of 0 at distance  and is the point closest to 0 up to now, and so on and so forth (for more details see [9] ). The above implies that the first return map in the interval
and is the point closest to 0 up to now, and so on and so forth (for more details see [9] ). The above implies that the first return map in the interval  (which is
(which is 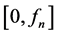 or
or  according whether
according whether  is even or odd) is the rotation through the angle
is even or odd) is the rotation through the angle . Finally, one has the equivalence:
. Finally, one has the equivalence:
 (2.26)
(2.26)
In addition, for each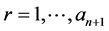 , it holds
, it holds
 (2.27)
(2.27)
The three distance theorem. The points  with
with  partition the unit circle into
partition the unit circle into  intervals. A classical result (see e.g. [10] ), which can be easily obtained by induction using the above construction, is that the possible lengths of these intervals are organized according to the Farey convergents in the following way:
intervals. A classical result (see e.g. [10] ), which can be easily obtained by induction using the above construction, is that the possible lengths of these intervals are organized according to the Farey convergents in the following way:
• If  then there are two distinct lengths:
then there are two distinct lengths:  and
and 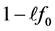 (which become
(which become  and
and  when
when ).
).
• If  for some
for some  and
and  then there are at most three lengths:
then there are at most three lengths: ,
,  and
and , the last of which disappears when
, the last of which disappears when .
.
We point out that in the second case above there are two intervals, chosen from among those having the smallest lengths:

which have 0 as their common endpoint. We then see that the approximations (26) and (27) are the same as shrinking one of these intervals to zero. Moreover, the fractions 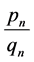 and
and  are the two successive elements of
are the two successive elements of  having
having  between them (see also Remark 2.3).
between them (see also Remark 2.3).
2.2. Growth of Denominators
The Gauss map  is defined as
is defined as
 (2.28)
(2.28)
It is well known that  has an a.c. invariant ergodic probability measure
has an a.c. invariant ergodic probability measure  given by
given by
 (2.29)
(2.29)
A short reflection shows that  or else
or else
 (2.30)
(2.30)
From this we obtain at once
 (2.31)
(2.31)
where the numbers  have been introduced in (2.22). Therefore
have been introduced in (2.22). Therefore

and, by the ergodic theorem, we have for 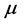 -almost all
-almost all  and then almost everywhere,
and then almost everywhere,
 (2.32)
(2.32)
Since  and thus
and thus  another consequence of (2.30) is that
another consequence of (2.30) is that

and therefore using (2.31)
 (2.33)
(2.33)
Putting together (2.32) and (2.33) we get the classical theorem of Lévy

On the other hand we may expect the growth of FC’s denominator to be subexponential. Indeed, let
 with
with  be the m-th FC. Its denominator satisfies
be the m-th FC. Its denominator satisfies . It is a result of Khinchin and Lévy (see [1] ) that
. It is a result of Khinchin and Lévy (see [1] ) that

Combining the above we get the following
Lemma 2.4
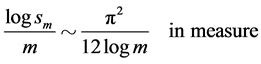
Of course there are special behaviours: take , then
, then  and both are equal to the n-th Fibonacci number. Hence
and both are equal to the n-th Fibonacci number. Hence  converge to
converge to .
.
3. A Walk on the Farey Tree
Having fixed , let
, let  be the ascending sequence of irreducible fractions between 0 and 1 constructed inductively in the following way: set first
be the ascending sequence of irreducible fractions between 0 and 1 constructed inductively in the following way: set first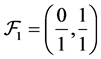 , then
, then  is obtained from
is obtained from  by inserting among each pair of neighbours
by inserting among each pair of neighbours  and
and  in
in  their child
their child  as in (2.13). Thus
as in (2.13). Thus

and so on. The elements of  are called again Farey fractions. Evidently
are called again Farey fractions. Evidently .
.
Remark 3.1 It has been shown in ([11] , Thm 2.6) that the set  becomes equidistributed as
becomes equidistributed as . More specifically, the probability measure
. More specifically, the probability measure 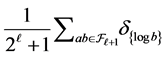 converges to the Lebesgue measure on
converges to the Lebesgue measure on
 .
.
Definition 3.2 For 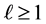 we say that a Farey fraction
we say that a Farey fraction  has rank
has rank  if
if .
.
We also define the . For
. For  there are exactly
there are exactly  Farey fractions of rank
Farey fractions of rank 
and their sum is equal to . Recall that every rational number
. Recall that every rational number  has a unique finite continued fraction expansion
has a unique finite continued fraction expansion  with
with  [2] . The validity of the following relation will arise straightforwardly in the sequel:
[2] . The validity of the following relation will arise straightforwardly in the sequel:
Lemma 3.3

Remark 3.4 Note that, according to the above Lemma, the cardinality  of
of  can be interpreted as the number of choices of integers
can be interpreted as the number of choices of integers , with
, with  and so that
and so that  for
for ,
, 
and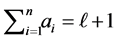 . Indeed, for each fixed
. Indeed, for each fixed 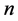 the number of such choices is
the number of such choices is , then sum over
, then sum over
 .
.
It is also easy to realize that all Farey fractions which fall in the interval  have rank greater than or equal to
have rank greater than or equal to , whereas their continued fraction expansion starts with
, whereas their continued fraction expansion starts with .
.
An interesting object is the Farey tree  whose vertex-set is
whose vertex-set is  and which is constructed as follows (see Figure 2):
and which is constructed as follows (see Figure 2):
• every column in  contains one entry (vertex or node);
contains one entry (vertex or node);
• for  the
the  -th row is
-th row is ;
;
• the node , representing the interval
, representing the interval , is connected by edges to its left child
, is connected by edges to its left child  and right child
and right child  in the underlying row.
in the underlying row.
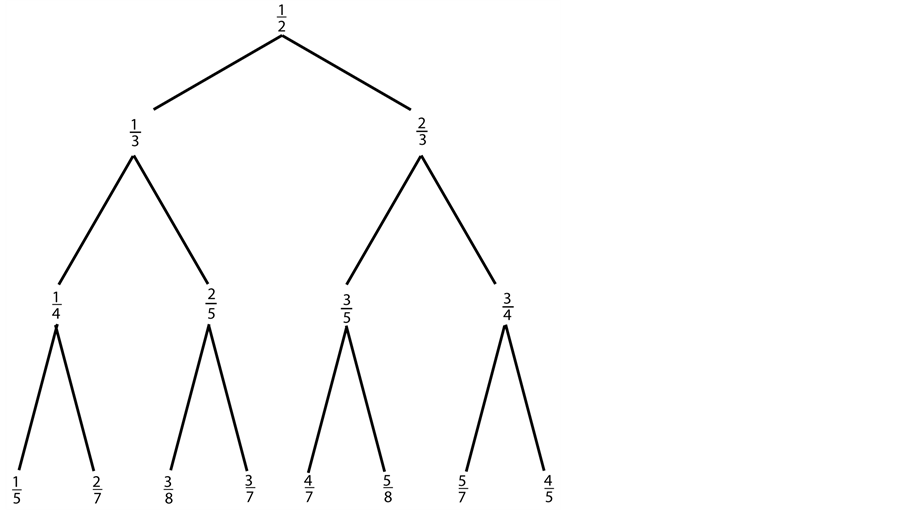
Figure 2. The first four levels of the Farey tree.
Note that the fractions  and
and  play the role of ancestors when using the Farey sum to obtain one row from the previous one. Besides the Farey sum, an alternative way to construct recursively the entries of
play the role of ancestors when using the Farey sum to obtain one row from the previous one. Besides the Farey sum, an alternative way to construct recursively the entries of  is as follows.
is as follows.
Definition 3.5 Given  its descendants are the symmetrical entries of
its descendants are the symmetrical entries of  given by
given by  and
and respectively.
respectively.
Lemma 3.6 The collection of all descendants of the entries of a given row in  is precisely the underlying row.
is precisely the underlying row.
Proof. If  then
then  and
and . Therefore
. Therefore
 and the claim follows.
and the claim follows. 
Remark 3.7 If  and
and  then
then  and
and .
.
3.1. The  Coding
Coding
Every rational number in  appears exactly once in the above construction and corresponds to a unique finite path on
appears exactly once in the above construction and corresponds to a unique finite path on  starting at the root node
starting at the root node  and whose number of vertices equals the rank of the rational number. We can code this path in the following way: first, any
and whose number of vertices equals the rank of the rational number. We can code this path in the following way: first, any  can be uniquely decomposed as3
can be uniquely decomposed as3
 (3.1)
(3.1)
and the unimodular relations
 (3.2)
(3.2)
plainly hold. The neighbours  and
and  are thus the ‘parents’ of
are thus the ‘parents’ of  in
in  and we may accordingly identify
and we may accordingly identify
 (3.3)
(3.3)
with
 (3.4)
(3.4)
Note that the left column bears on the right parent and viceversa. Thus
 (3.5)
(3.5)
On the other hand, any  as above has a unique pair of (left and right) children, given by
as above has a unique pair of (left and right) children, given by
 (3.6)
(3.6)
respectively. In order to generate them we set
 (3.7)
(3.7)
Note that for 
 (3.8)
(3.8)
and also
 (3.9)
(3.9)
Moreover, we have
 (3.10)
(3.10)
and
 (3.11)
(3.11)
In other words, the matrices L and R, when acting from the right, move to the left and right child in , respectively. Moreover, it is plain that given
, respectively. Moreover, it is plain that given  we have
we have  and
and . We have thus proved the following Proposition 3.8 To each entry
. We have thus proved the following Proposition 3.8 To each entry  there corresponds a unique element
there corresponds a unique element  which, in turn, can be uniquely presented as
which, in turn, can be uniquely presented as
 (3.12)
(3.12)
where the number of terms in the product  is equal to
is equal to 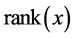 and Mi = L or Mi = R according whether the i-th turn, along the descending path in
and Mi = L or Mi = R according whether the i-th turn, along the descending path in  which starts from the root node
which starts from the root node  and reaches xgoes left or right.
and reaches xgoes left or right.
Remark 3.9 By the way, the matrices L and R induce the so called Farey tesselation of the upper half plane  (see [12] ).
(see [12] ).
Example.  is the right child of
is the right child of , which is the right child of
, which is the right child of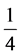 , which is the left child of
, which is the left child of , which is the left child of
, which is the left child of . Thus
. Thus

For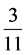 , which is the left child of
, which is the left child of , we find
, we find

Note that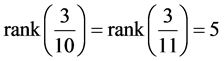 .
.
To any given irrational number  we may associate a unique infinite path on
we may associate a unique infinite path on , and thus a unique semi-infinite word in
, and thus a unique semi-infinite word in . Bearing in mind the continued fraction expansion (2.1) of x, let
. Bearing in mind the continued fraction expansion (2.1) of x, let

the first FC of x. In order to reach it from the top of  we need the block
we need the block . Whence we code x through the map
. Whence we code x through the map 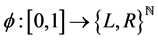 defined by
defined by
 (3.13)
(3.13)
where  or
or  according whether the i-th turn along the infinite path in
according whether the i-th turn along the infinite path in  which starts from
which starts from
 and approaches x along the sequence of successive FC’s goes left or right. This coding is faithful to the binary structure of
and approaches x along the sequence of successive FC’s goes left or right. This coding is faithful to the binary structure of  but apparently not so much to the continued fraction expansion of x. To make the latter more transparent we may note that, according to the characterization of the FC’s given above (see (2.15) and (2.16)), the symbols L and R in (3.13) come in blocks whose lengths are given by nothing but the partial quotients
but apparently not so much to the continued fraction expansion of x. To make the latter more transparent we may note that, according to the characterization of the FC’s given above (see (2.15) and (2.16)), the symbols L and R in (3.13) come in blocks whose lengths are given by nothing but the partial quotients  of
of . More precisely, a short reflection shows that the following rule is in force: the first block is such that
. More precisely, a short reflection shows that the following rule is in force: the first block is such that  if
if . Moreover, for
. Moreover, for  let
let

then we have

In other words, we have the coding
 (3.14)
(3.14)
Furthermore we set  and
and . More generally, we note that each rational x has two infinite paths which agree down to node
. More generally, we note that each rational x has two infinite paths which agree down to node : they are those starting with the finite sequence coding the path to reach x from the root node and terminating with either
: they are those starting with the finite sequence coding the path to reach x from the root node and terminating with either  or
or . We shall agree that
. We shall agree that  terminates with
terminates with  or
or  according whether the number of its (finite) partial quotients is even or odd. On the other hand, for notational simplicity’ sake we shall assume this agreement only implicitly. We summarize the above in the following Theorem 3.10 To
according whether the number of its (finite) partial quotients is even or odd. On the other hand, for notational simplicity’ sake we shall assume this agreement only implicitly. We summarize the above in the following Theorem 3.10 To  with continued fraction expansion
with continued fraction expansion  there corresponds a unique sequence
there corresponds a unique sequence  given by
given by  which represents an infinite path on
which represents an infinite path on 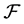 whose sequence of vertices starting from the
whose sequence of vertices starting from the  -th is precisely the sequence
-th is precisely the sequence  of FC’s of x. Moreover, if
of FC’s of x. Moreover, if 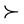 denotes the lexicographic order on
denotes the lexicographic order on 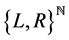 then
then

An simple consequence of the above construction is the following result.
Proposition 3.11 Let  with
with  and
and 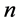 even. Then its left and right children in
even. Then its left and right children in  are given by
are given by  and
and , respectively. If instead
, respectively. If instead  is odd the expansions for
is odd the expansions for  and
and  have to be interchanged.
have to be interchanged.
Proof. Since  is even we can write
is even we can write
 (3.15)
(3.15)
Therefore

which yield the claim. A similar reasoning applies for  odd.
odd. 
3.2. The {A, B} Coding
Using (3.9) we can write
 (3.16)
(3.16)
On the other hand we have 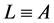 and (see (2.4))
and (see (2.4))
 (3.17)
(3.17)
This defines a recoding  so that
so that
 (3.18)
(3.18)
The FC  of
of , which has rank
, which has rank , will then be expressed as
, will then be expressed as
 (3.19)
(3.19)
or else
 (3.20)
(3.20)
Note that both expansions have exactly  terms and the latter agrees with (2.17) once we interpret the l.h.s. of
terms and the latter agrees with (2.17) once we interpret the l.h.s. of
(2.17) as the FC  of x, that is taking the Farey sum of the columns in the same spirit as (3.3).
of x, that is taking the Farey sum of the columns in the same spirit as (3.3).
Example. The example with 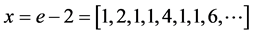 discussed above, which yields
discussed above, which yields
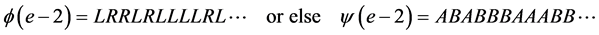
can be used to check step by step what we are claiming here. For example its FC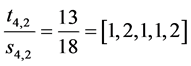 , which has rank 6, can be expressed as
, which has rank 6, can be expressed as

3.3. The Farey Shift and Its Relatives
So far, a sequence in  starting with the symbol R has no image in
starting with the symbol R has no image in  with
with . Let us make the identification
. Let us make the identification
 (3.21)
(3.21)
and denote by  the half-space of
the half-space of  so obtained. We can write
so obtained. We can write
 (3.22)
(3.22)
We see that the map  is a bijection between
is a bijection between 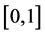 and
and .
.
Let  be the Farey shift map defined by
be the Farey shift map defined by
 (3.23)
(3.23)
Note that, besides  the only fixed point of
the only fixed point of  is given by the sequence
is given by the sequence  which is the image with
which is the image with  of
of , the golden mean. This map acts on points in
, the golden mean. This map acts on points in  by reducing their rank of one unit.
by reducing their rank of one unit.
For example, since , with the identifications made above we have
, with the identifications made above we have
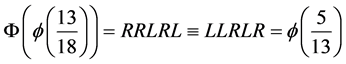




Let us define the Farey map  given by
given by
 (3.24)
(3.24)
Its name can be related to the easily verified observation that the set of pre-images  coincides with
coincides with  for all
for all . Note also that the
. Note also that the  -th row of the Farey tree is precisely
-th row of the Farey tree is precisely . In particularthis implies that
. In particularthis implies that .
.
Proposition 3.12 Let  be the coding described above. Then
be the coding described above. Then

Proof. If  then
then  and
and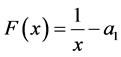 . If instead
. If instead  then
then  and
and
 . Therefore,
. Therefore,
 (3.25)
(3.25)
with . The claim now follows from (3.23) and (3.21).
. The claim now follows from (3.23) and (3.21). 
3.3.1. The Gauss and Fibonacci Maps
The map F has (at least) two induced versions: the first one is the Gauss map  already introduced in (2.28), which for
already introduced in (2.28), which for  can be written as
can be written as
 (3.26)
(3.26)
Recall that
 (3.27)
(3.27)
Noting that
 (3.28)
(3.28)
we see that G is obtained by iterating F once plus the number of times necessary to reach the interval . The second one is the Fibonacci map H and is defined by iterating F once plus the number of times necessary to reach the interval
. The second one is the Fibonacci map H and is defined by iterating F once plus the number of times necessary to reach the interval . Let
. Let  and
and  for
for  be the Fibonacci numbers. Then, for
be the Fibonacci numbers. Then, for ,
,
 (3.29)
(3.29)
with
 (3.30)
(3.30)
In this case it is easy to check that if  then
then
 (3.31)
(3.31)
A sketch of the map F along its induced versions G and H is given in Figure 3.
Given  we may define the Möbius transformation
we may define the Möbius transformation

By the above, given  the point
the point  is but
is but  and for
and for  we have
we have
 (recall that
(recall that ). But what happens if
). But what happens if  so that
so that ?
?
To see this we put
 (3.32)
(3.32)
We have

Therefore, noting that , for
, for  we have
we have . To summarize we can represent the action of F as
. To summarize we can represent the action of F as



Figure 3. The Farey map and its induced Fibonacci (upper) and Gauss (lower) maps.
that of G as

and that of H as

3.3.2. The Modified Farey Map
Finally we introduce the modified Farey map 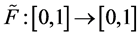 given by
given by
 (3.33)
(3.33)
This map preserves orientation and has two indifferent fixed points, at 0 and 1. The advantage of using  instead of
instead of 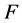 is that one can retrace the path from a leaf
is that one can retrace the path from a leaf  back to the root
back to the root . More precisely, for
. More precisely, for  let (cf. Proposition 3.8)
let (cf. Proposition 3.8)  be the element which uniquely represents x in
be the element which uniquely represents x in . Then one easily sees that the following rule is in force: if
. Then one easily sees that the following rule is in force: if  then
then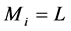 ,
,  then
then , for
, for  with
with  so that
so that .
.
4. The Minkowski Question Mark
Given a number  with continued fraction expansion
with continued fraction expansion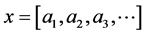 , one may ask what is the number obtained by interpreting the sequence
, one may ask what is the number obtained by interpreting the sequence  (see (3.14)) as the binary expansion of a real number in
(see (3.14)) as the binary expansion of a real number in . The number so obtained is denoted
. The number so obtained is denoted  and writes
and writes
 (4.1)
(4.1)
or, which is the same,
 (4.2)
(4.2)
For instance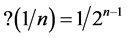 , for all
, for all  (see Figure 4). Setting
(see Figure 4). Setting  and
and  one has the following properties for the function
one has the following properties for the function  (see [13] -[16] ):
(see [13] -[16] ):
•  is strictly increasing from 0 to 1 and Hölder continuous of exponent
is strictly increasing from 0 to 1 and Hölder continuous of exponent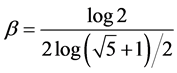 ;
;
• x is rational iff  is of the form
is of the form , with k and s integers;
, with k and s integers;
• x is a quadratic irrational iff  is a (non-dyadic) rational;
is a (non-dyadic) rational;
•  is a singular function: its derivative vanishes Lebesgue-almost everywhere.
is a singular function: its derivative vanishes Lebesgue-almost everywhere.
The following additional properties easily follow from the definition.
Lemma 4.1  satisfies the functional equations
satisfies the functional equations


Proof. Assuming that  we write
we write  with
with 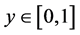 and
and . Setting moreover
. Setting moreover  we have
we have  and
and . The assertion now follows by direct application of (4.2).
. The assertion now follows by direct application of (4.2). 
Let us now see how 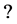 acts on Farey fractions. We have already seen that
acts on Farey fractions. We have already seen that

More generally, for any pair  and
and  of consecutive Farey fractions the function ? equates their child to the arithmetic average:
of consecutive Farey fractions the function ? equates their child to the arithmetic average:
 (4.3)
(4.3)
One sees that the function ? maps the Farey tree  to the dyadic tree
to the dyadic tree  defined as follows: having fixed
defined as follows: having fixed , let
, let  be the ascending sequence of fractions of the form
be the ascending sequence of fractions of the form ,
, . We have
. We have

and so on. Then  is the same graph as
is the same graph as  with the
with the  -th row replaced by
-th row replaced by . An immediate consequence of the fact that
. An immediate consequence of the fact that  is that
is that  is the asymptotic distribution function of the sequence of Farey fractions:
is the asymptotic distribution function of the sequence of Farey fractions:
Theorem 4.2 Since

then

Remark 4.3 This result can be also deduced as a consequence of a more general result obtained in [17] using a suitable enumeration of the rationals in . As for the convergence of the atomic measure concentrated on
. As for the convergence of the atomic measure concentrated on  to
to  see [11] and [18] .
see [11] and [18] .
As a further immediate consequence we get that the Fourier-Stieltjes coefficients of  are as in the following
are as in the following
Corollary 4.4 Let

then

Finally, a short reflection using the definition (4.1) shows that ? conjugates the Farey map F and the modified Farey map  to the tent map
to the tent map
 (4.4)
(4.4)
and the doubling map , respectively. Indeed, for any
, respectively. Indeed, for any  with
with  we have
we have
 (4.5)
(4.5)
and
 (4.6)
(4.6)
where  and
and . A similar reasoning applies for D. Putting together the above, (3.25) and (4.1) we then get the following commutative diagrams
. A similar reasoning applies for D. Putting together the above, (3.25) and (4.1) we then get the following commutative diagrams
Theorem 4.5

This implies that the measure  is invariant under both maps F and
is invariant under both maps F and , and its entropy is equal to
, and its entropy is equal to . This makes
. This makes  the measure of maximal entropy for F and
the measure of maximal entropy for F and . Being zero at every rational point
. Being zero at every rational point 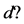 is of course singular w.r.t. Lebesgue. More specifically,
is of course singular w.r.t. Lebesgue. More specifically,  is concentrated on a subset
is concentrated on a subset  having Hausdorff dimension
having Hausdorff dimension  (see [14] ). In view of (3.25), the above has the following straightforward consequence Lemma 4.6 If x is drawn from
(see [14] ). In view of (3.25), the above has the following straightforward consequence Lemma 4.6 If x is drawn from  according to the singular measure
according to the singular measure , then the partial quotients
, then the partial quotients 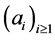 of
of  form a sequence of i.i.r.v.’s with
form a sequence of i.i.r.v.’s with .
.
It is moreover easy to realize that F and  have also absolutely continuous (not normalizable) invariant measures, with densities
have also absolutely continuous (not normalizable) invariant measures, with densities 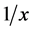 and
and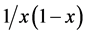 , respectively.
, respectively.
Finally, the conjugacy of Theorem 4.5 has been used in [19] to construct a correspondence between the parameter spaces of  -continued fraction transformations and unimodal maps.
-continued fraction transformations and unimodal maps.
5. Transfer Operators and Partition Functions
To a given matrix  and complex parameter
and complex parameter  one can associate the positive operator
one can associate the positive operator
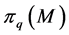 acting on the right as [20]
acting on the right as [20]
 (5.1)
(5.1)
For example we have
 (5.2)
(5.2)
The operator 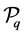 associated in this way to the map
associated in this way to the map  turns out to be the transfer operator acting as
turns out to be the transfer operator acting as
 (5.3)
(5.3)
Of special significance is the (Perron-Frobenius) operator  which satisfies
which satisfies
 (5.4)
(5.4)
and has norm at most one in the Banach space . A function
. A function 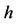 is the density of an absolutely continuous invariant measure for F if and only if
is the density of an absolutely continuous invariant measure for F if and only if . In this case we find
. In this case we find , which however does not lie in
, which however does not lie in  (see [21] ).
(see [21] ).
Let f be an eigenfunction of 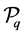 analytic in the half-plane
analytic in the half-plane . It satisfies
. It satisfies
 (5.5)
(5.5)
and also
 (5.6)
(5.6)
Therefore the eigenvalue equation is equivalent to the three-term equation
 (5.7)
(5.7)
which is a generalisation of the Lewis functional equation (with ) studied in number theory (see [20] [22] ). The study of this generalized equation has been initiated in [23] .
) studied in number theory (see [20] [22] ). The study of this generalized equation has been initiated in [23] .
Remark 5.1 In the context of the thermodynamic formalism, once a one-sided shift 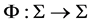 and a potential function
and a potential function  are given one defines a transfer operator
are given one defines a transfer operator  on
on  by
by

which plays a key role in the study of equilibrium states for  and their properties [24] [25] . In particular, one defines
and their properties [24] [25] . In particular, one defines

and it turns out that if  decays exponentially then there is a unique mixing equilibrium state.
decays exponentially then there is a unique mixing equilibrium state.
Relying on the above discussion it is now easy to see that  with
with

In order to compute  we have to consider points sharing the same path up to the k-th row of
we have to consider points sharing the same path up to the k-th row of . Take for instance
. Take for instance  and
and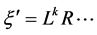 . Then a short reflection yields, for
. Then a short reflection yields, for ,
,

We therefore see that although  (so that
(so that  is uniformly continuous)
is uniformly continuous)  it is not even of summable variation. This entails that
it is not even of summable variation. This entails that  has indeed two equilibrium states, thus exhibiting a phase transition (see [26] ).
has indeed two equilibrium states, thus exhibiting a phase transition (see [26] ).
Next, we express the n-th iterate of  as
as
 (5.8)
(5.8)
where . We have
. We have  so that, in particular, putting
so that, in particular, putting  we get
we get
 (5.9)
(5.9)
and
 (5.10)
(5.10)
Lemma 5.2 Let  be the sequence of functions defined by
be the sequence of functions defined by  and
and

For each fixed  we have that
we have that  determines a bijection between
determines a bijection between  and the set of denominators of the elements of
and the set of denominators of the elements of  (considered as an ordered set).
(considered as an ordered set).
Proof. The proof is just a straightforward verification. Suppose for instance that  with
with
 , so that
, so that . Then by (5.9) and (5.10)
. Then by (5.9) and (5.10)  is given by a product with
is given by a product with  factors of the type
factors of the type  where r = a if
where r = a if , r = b otherwise. The result now readily follows by lemma 3.6.
, r = b otherwise. The result now readily follows by lemma 3.6. 
Remark 5.3 The rank of the elements of 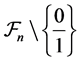 with denominator
with denominator  is given by
is given by
 with the convention
with the convention . The smallest of the above denominators is 1, it has rank 0 and is obtained as
. The smallest of the above denominators is 1, it has rank 0 and is obtained as . The two largest ones are equal to the
. The two largest ones are equal to the  -st Fibonacci number
-st Fibonacci number
 . They are symmetrical w.r.t
. They are symmetrical w.r.t , have rank
, have rank  and are obtained as
and are obtained as
 and
and , respectively. More generally, it is not difficult to see that the following equivalence is in force: suppose that the element
, respectively. More generally, it is not difficult to see that the following equivalence is in force: suppose that the element  has rank
has rank  so that
so that  for some
for some  and
and , then the same denominator
, then the same denominator , but corresponding to the symmetrical fraction
, but corresponding to the symmetrical fraction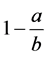 , is obtained as
, is obtained as  with
with .
.
A direct consequence of the above lemma is the following
Theorem 5.4

Remarkably, the above sum is equal to the partition function  at (inverse) temperature
at (inverse) temperature  of the number-theoretical spin chain introduced by Andreas Knauf in [27] . For
of the number-theoretical spin chain introduced by Andreas Knauf in [27] . For 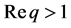 we have (see [28] )
we have (see [28] )
 (5.11)
(5.11)
Note that for  the above limit diverges. This reflects the fact that the invariant density for the Farey map F, that is the fixed point of the operator
the above limit diverges. This reflects the fact that the invariant density for the Farey map F, that is the fixed point of the operator , is the function
, is the function .
.
Let us define the pressure function  as
as
 (5.12)
(5.12)
Since the sum in Thm. 5.4 has  terms we see that
terms we see that  (this is the topological entropy of the map
(this is the topological entropy of the map ). More generally let
). More generally let  denote the sequence of denominators of the elements of
denote the sequence of denominators of the elements of
 when the latters are arranged in increasing order in
when the latters are arranged in increasing order in , so that
, so that
 (5.13)
(5.13)
The ratio  can be interpreted as the moment of order
can be interpreted as the moment of order  of the size of the denominators in
of the size of the denominators in
 .
.  is plainly non-increasing and for
is plainly non-increasing and for 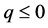 satisfies
satisfies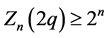 . Moreover we have
. Moreover we have

with  for all
for all . Noting that
. Noting that  we get for
we get for 

Since  this yields
this yields
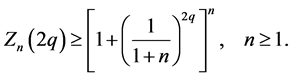 (5.14)
(5.14)
Thus, for all ,
,
 (5.15)
(5.15)
In addition, since  is non-increasing and
is non-increasing and  (because the spectral radius of
(because the spectral radius of  is 1, see above) we have
is 1, see above) we have  for
for . Note that the same conclusion follows at once from the fact that
. Note that the same conclusion follows at once from the fact that  is finite for
is finite for  (see (11)).
(see (11)).
Remark 5.5 It holds  where
where  is the free energy of the Knauf model. In the context of thermodynamic formalism the pressure
is the free energy of the Knauf model. In the context of thermodynamic formalism the pressure  is a central object. In particular it is used as a generator of averages: its first derivative
is a central object. In particular it is used as a generator of averages: its first derivative , wherever it exists, yields the mean of the function
, wherever it exists, yields the mean of the function  w.r.t. the equilibrium measure
w.r.t. the equilibrium measure , which can be defined as the weak *-limit point of atomic measures supported on periodic points of F weighted with the function
, which can be defined as the weak *-limit point of atomic measures supported on periodic points of F weighted with the function  [24] . Note that
[24] . Note that  for
for  and
and  as
as . On the other hand we have already seen that
. On the other hand we have already seen that  and
and  is called measure of maximal entropy. Higher derivatives of
is called measure of maximal entropy. Higher derivatives of  are connected to (sums of) higher correlation functions, see [25] [29] .
are connected to (sums of) higher correlation functions, see [25] [29] .
Let us now study the asymptotic behaviour of  for
for . To this end, we notice that if, instead of
. To this end, we notice that if, instead of , we evaluate the iterate
, we evaluate the iterate  at
at , all sequences
, all sequences  in (5.8) yield paths which end up at the same row of the Farey tree. The same argument leading to Theorem 5.4 now yields the following
in (5.8) yield paths which end up at the same row of the Farey tree. The same argument leading to Theorem 5.4 now yields the following
Corollary 5.6
 (5.16)
(5.16)
By Thm. 5.4 and (5.16) we obtain
 (5.17)
(5.17)
so that we can directly apply the results obtained by Thaler in [30] to get4
Lemma 5.7

Lastly, noting that

one may then use , along with Lemma 3.6, to proceed inductively with
, along with Lemma 3.6, to proceed inductively with  in (5.8), and obtain the following general expression for
in (5.8), and obtain the following general expression for  with
with .
.
Theorem 5.8 For all  and
and  we have
we have

We refer to [31] for further generalisations and applications (see also [32] ).
The Partition Function for Negative Integer Temperatures
Finally, we compute the value of the partition function  for some some specific value of the temperature. Related results are discussed in [33] (see also [34] ).
for some some specific value of the temperature. Related results are discussed in [33] (see also [34] ).
Lemma 5.9 We have, for all ,
,



Proof. The first identity is trivial. The second one follows immediately from  along with (5.14), which gives the recursion
along with (5.14), which gives the recursion . As for the third one, we can reason as follows: let us denote
. As for the third one, we can reason as follows: let us denote
 and
and . Then (5.14) yields
. Then (5.14) yields . Moreover, we have
. Moreover, we have

This yields the recursion  with
with  and
and  and the claim easily follows
and the claim easily follows . The above result indicates a general argument to work out
. The above result indicates a general argument to work out  for any
for any : setting
: setting  and
and  one has
one has

and

This yields a k-dimensional recursion
 (5.18)
(5.18)
with  matrix
matrix

and initial condition
 (5.19)
(5.19)
By Perron-Frobenius theorem the matrix  has a simple real positive maximal eigenvalue
has a simple real positive maximal eigenvalue  whose eigenvector
whose eigenvector  has strictly positive components. This immediately yields
has strictly positive components. This immediately yields
 (5.20)
(5.20)
More specifically, by the above the exact behaviour of  can be obtained by standard linear algebra. If for instance
can be obtained by standard linear algebra. If for instance  can be diagonalized with spectrum
can be diagonalized with spectrum  and corresponding eigenvectors
and corresponding eigenvectors , then we can expand
, then we can expand  so that (5.18) and (5.19) yield
so that (5.18) and (5.19) yield
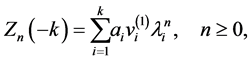 (5.21)
(5.21)
where  denotes the first component of
denotes the first component of . On the other hand, as we shall see in the forthcoming example,
. On the other hand, as we shall see in the forthcoming example,  is not always diagonalizable.
is not always diagonalizable.
Examples. For  we find
we find

so that by (5.20)  and using (5.21) one easily recover the result of Lemma 5.9 for
and using (5.21) one easily recover the result of Lemma 5.9 for .
.
For  we get
we get

In this case (5.21) does not hold but one easily finds

and .
.
The case  is still different, yielding
is still different, yielding

NOTES
1Good general sources on this subject are -.

2The origin of these names traces back to Cauchy, who proved this property after it was observed by John Farey in 1816 , and named “Farey series” the numbers obtained in this way.

3All fractions are supposed in lowest terms.

4We say that an and bn are asymptotically equivalent, denoted as an ~ bn, if the quotient an/bn tends to unity as n approaches ∞.