Integral Sequences of Infinite Length Whose Terms Are Relatively Prime ()
1. Introduction
The numbers  are called Fermat numbers. Fermat conjectured that Fn were all prime numbers. One has
are called Fermat numbers. Fermat conjectured that Fn were all prime numbers. One has ,
,  ,
,  ,
, 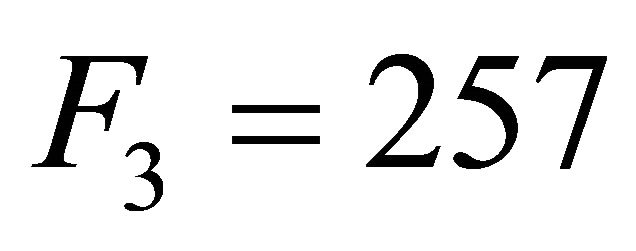 ,
,  and
and . By now, no Fermat prime has been found except for
. By now, no Fermat prime has been found except for . In Euclid’s books was given the proof of existence of infinitely many prime numbers. By proving G.C.D.
. In Euclid’s books was given the proof of existence of infinitely many prime numbers. By proving G.C.D.  if
if , Pólya gave another proof of that, cf. ([2], Theorem 16, p. 14) and ([3], exercise (viii), p. 7). Weil and Rosenlicht ([1], p. 15) considered not only
, Pólya gave another proof of that, cf. ([2], Theorem 16, p. 14) and ([3], exercise (viii), p. 7). Weil and Rosenlicht ([1], p. 15) considered not only  but also
but also  for any rational integer c.
for any rational integer c.
Let n be any positive integer, and let  be any primitive n-th root of unity. Let
be any primitive n-th root of unity. Let
 . Then the number of
. Then the number of  where
where  denotes the Euler function. Let
denotes the Euler function. Let  denote the n-th cyclotomic polynomial over Q. Namely,
denote the n-th cyclotomic polynomial over Q. Namely, 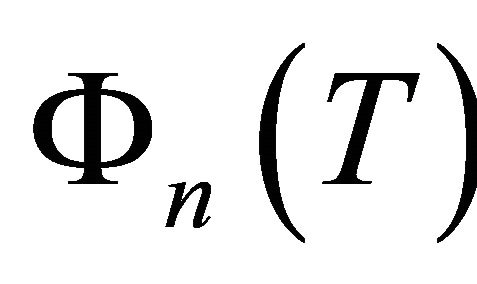 denotes the polynomial
denotes the polynomial of the minimum degree whose roots contain
of the minimum degree whose roots contain  and whose leading coefficient is 1. One has that
and whose leading coefficient is 1. One has that  does not depend on choice of
does not depend on choice of 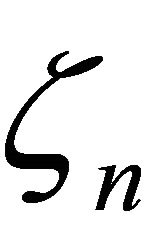 in
in , that
, that
 and that
and that  (see e.g. [4-8]). Below in this paper we write
(see e.g. [4-8]). Below in this paper we write . We let G.C.D. denote “greatest common divisor” as usual. One has
. We let G.C.D. denote “greatest common divisor” as usual. One has  Then exercise IV.3 in [1] asserts
Then exercise IV.3 in [1] asserts  (resp. 2)
(resp. 2)
for all positive integers m and n with  if c is even (resp. odd).
if c is even (resp. odd).
We generalize this. Let p denote any odd prime number, and let v denote any rational integer. In Theorem 2 in Section 3 below we show that
 (resp. p) for all positive integers m and n with
(resp. p) for all positive integers m and n with  if v is not congruent modulo p to 1 (resp. if v is congruent modulo p to 1). Our first proof of Theorem 2 uses Elementary Number Theory. Our second proof of Theorem 2 uses Algebraic Number Theory and Theory of Cyclotomic Fields. In Corollary 5 in Section 4 we also show that
if v is not congruent modulo p to 1 (resp. if v is congruent modulo p to 1). Our first proof of Theorem 2 uses Elementary Number Theory. Our second proof of Theorem 2 uses Algebraic Number Theory and Theory of Cyclotomic Fields. In Corollary 5 in Section 4 we also show that  for all positive integers m and n with
for all positive integers m and n with  and all rational integers v. In Corollary 4 in Section 3 we study also
and all rational integers v. In Corollary 4 in Section 3 we study also  where p and q are arbitrary odd prime numbers with
where p and q are arbitrary odd prime numbers with . The case of
. The case of
 is reduced to Theorem 2 since
is reduced to Theorem 2 since  for any non-negative integer u. Cf. Corollary 3 in Section 3.
for any non-negative integer u. Cf. Corollary 3 in Section 3.
In Section 2 (resp. 4) we consider

In Theorem 1 in Section 2 we show  for all positive integers m and n with
for all positive integers m and n with  and all rational integers a and b with
and all rational integers a and b with . In Theorem 3 in Section 4 we show
. In Theorem 3 in Section 4 we show  (resp. 2) for all positive integers m and n with
(resp. 2) for all positive integers m and n with  and all rational integers a and b with
and all rational integers a and b with  (resp.
(resp. ) and
) and . The case
. The case  of Theorem 3 gives a proof of Exercise IV.3 in [1].
of Theorem 3 gives a proof of Exercise IV.3 in [1].
2. On 
Recall . We show first Theorem 1. Let a and b be arbitrary rational integers with
. We show first Theorem 1. Let a and b be arbitrary rational integers with . Let
. Let  denote the sequence given by
denote the sequence given by  for all positive integers n. Then we have
for all positive integers n. Then we have  for all positive integers m and n with
for all positive integers m and n with .
.
Proof. We have
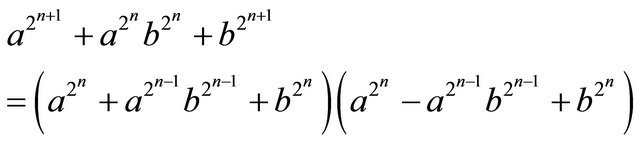
and

Hence  for all integers
for all integers  . We have also
. We have also

From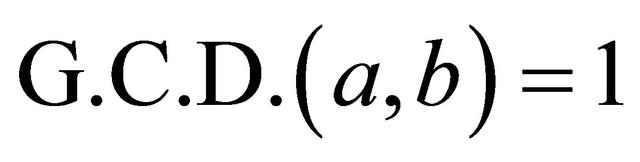 , factoring a and b into products of prime numbers, we have
, factoring a and b into products of prime numbers, we have
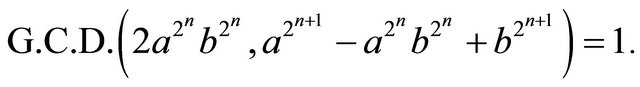
Hence  for all rational integers
for all rational integers . Namely
. Namely  for all rational integers
for all rational integers .
.
In Euclid’s books was given the proof of the classical well known theorem that there are infinitely many prime numbers. Theorem 1 above gives another proof of this theorem. For each positive integer m, let  denote a prime number dividing
denote a prime number dividing  in Theorem 1.
in Theorem 1.
Corollary 1. We have  if
if . There are infinitely many prime numbers.
. There are infinitely many prime numbers.
3. On 
Let p be any odd prime number and let n be any positive integer. Let  denote a primitive
denote a primitive  -th root of unity in
-th root of unity in . Recall
. Recall . It is a polynomial in
. It is a polynomial in  whose leading coefficient is 1. One has
whose leading coefficient is 1. One has
 , (see e.g. [4-8]). Let m and n be arbitrary positive integers with
, (see e.g. [4-8]). Let m and n be arbitrary positive integers with 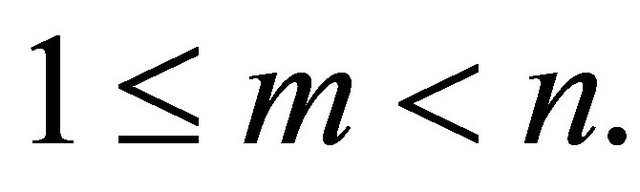 Since there are no common roots of
Since there are no common roots of  and
and 
in ,
,  in
in .
.
We have Proposition 1.  in
in 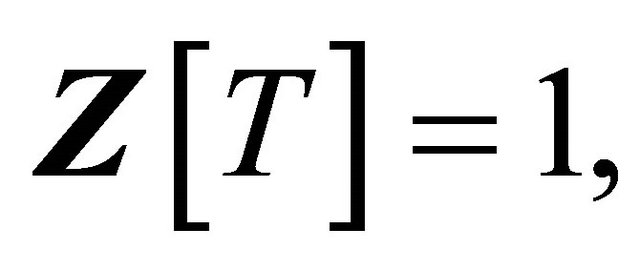 if
if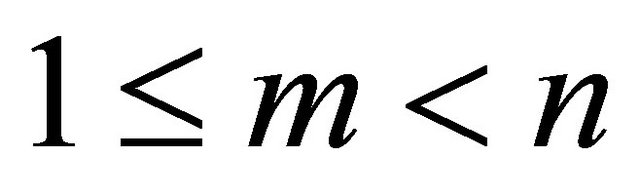 .
.
Proof. We have  and
and  are polynomials in
are polynomials in  whose leading coefficients are 1, (see e.g. [4-8]). Use Gauss Lemma for polynomials over the quotient ring of a factorial ring, (see e.g. ([5], pp. 181-182)). By applying it to
whose leading coefficients are 1, (see e.g. [4-8]). Use Gauss Lemma for polynomials over the quotient ring of a factorial ring, (see e.g. ([5], pp. 181-182)). By applying it to 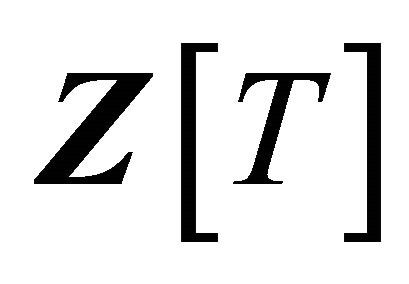 and
and ,
,  is factorial.
is factorial.
We may put  in
in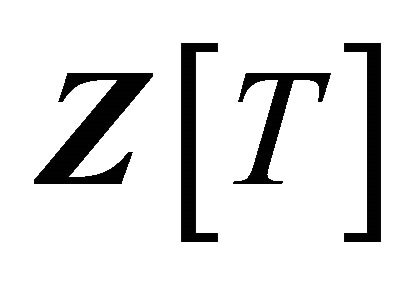 . If deg
. If deg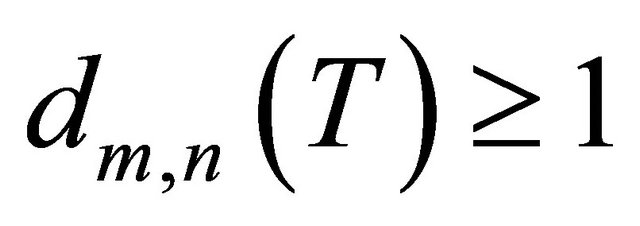 , this contradicts
, this contradicts  . We have
. We have
 . Since the leading coefficient of
. Since the leading coefficient of
 is 1,
is 1, . Proposition 1 is proven.
. Proposition 1 is proven.
Note
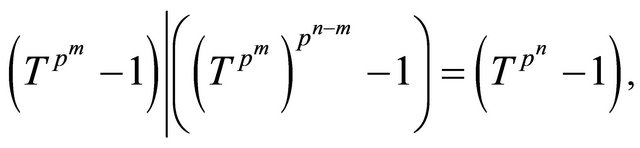
and

in  if
if . We have
. We have  in
in  if
if  and
and . One has
. One has

and , see e.g. [4-8]. We give Theorem 2. Let p be any odd prime number, and let v be any rational integer. Then we have the following.
, see e.g. [4-8]. We give Theorem 2. Let p be any odd prime number, and let v be any rational integer. Then we have the following.
Case 1 that v is not congruent modulo p to 1:

for all rational integers m and n with .
.
Case 2 that v is congruent modulo  to 1:
to 1:

for all rational integers m and n with .
.
We give two proofs. The first one uses Elementary Number Theory. The second one uses (local and global) Algebraic Number Theory and Theory of Cyclotomic Fields for which cf. [4-9].
Proof 1. We have . Put
. Put  We have
We have

and

There is a rational integer 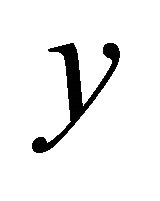 with
with  We have
We have  or p.
or p.
Since  divides
divides
 . Hence
. Hence
 or
or . (1)
. (1)
In Case 2: We have

We have also  Hence
Hence
 . Case 2 of Theorem 2 is proven.
. Case 2 of Theorem 2 is proven.
In Case 1: Let 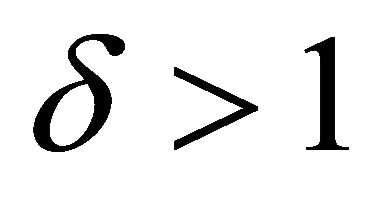 be any divisor of
be any divisor of . Then
. Then  We have
We have
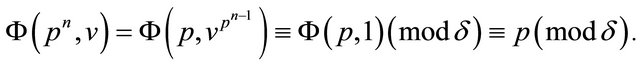
We shall show  does not divide
does not divide . Assume it were true that
. Assume it were true that . Then we would have
. Then we would have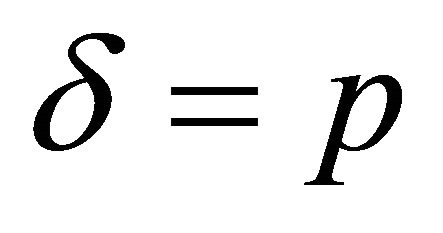 . We have
. We have 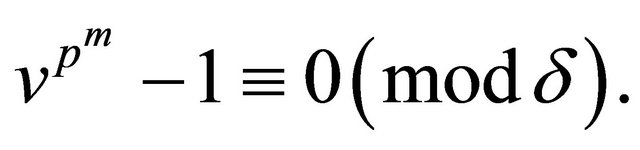 Therefore
Therefore
 and
and  would not divide v.
would not divide v.
It follows that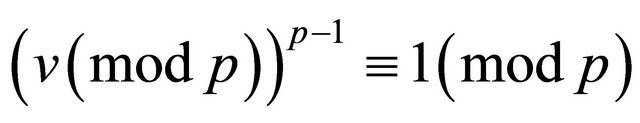 . The order of
. The order of  divides
divides  and
and . Hence
. Hence 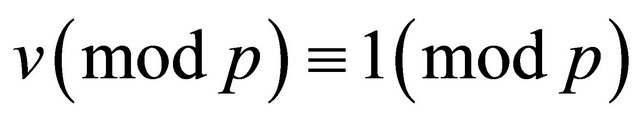 , which is a contradiction. Hence we have
, which is a contradiction. Hence we have 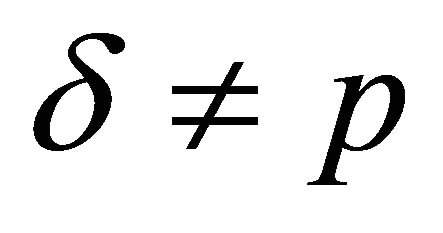 and
and  does not divide
does not divide . Hence
. Hence  does not divide
does not divide . Hence we get
. Hence we get
 . Since
. Since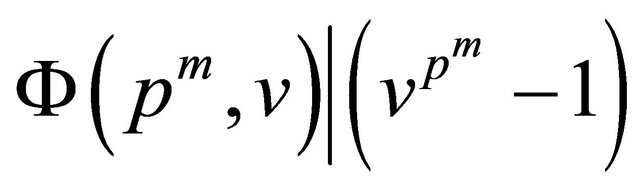 , we have
, we have 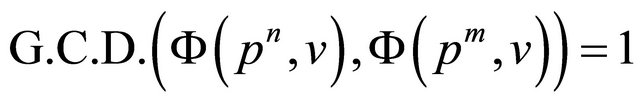 if
if . Case 1 of Theorem 2 is proven.
. Case 1 of Theorem 2 is proven.
We give another proof of Theorem 2.
Proof 2. Let  Recall
Recall

and
 .
.
Take  (resp.
(resp. ) arbitrarily. Let B denote the ring of the algebraic integers in
) arbitrarily. Let B denote the ring of the algebraic integers in . Let
. Let .
.
In Case 1: Now assume that there is such a prime ideal P of B that satisfies  and
and  Write
Write  and
and . We have
. We have  and
and  Let
Let  We have
We have 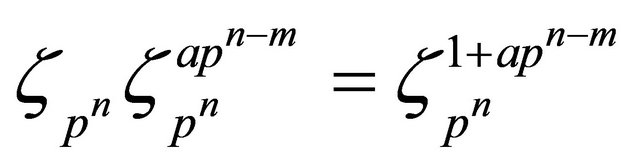 which is a primitive
which is a primitive 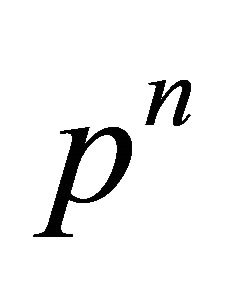 -th root of unity since p does not divide
-th root of unity since p does not divide 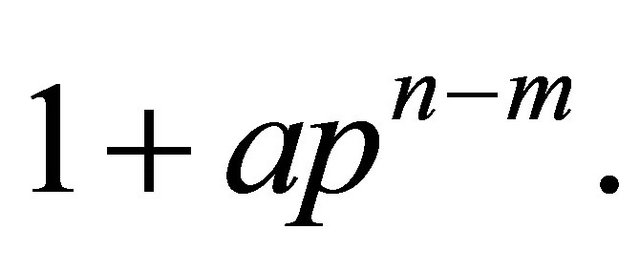 So
So 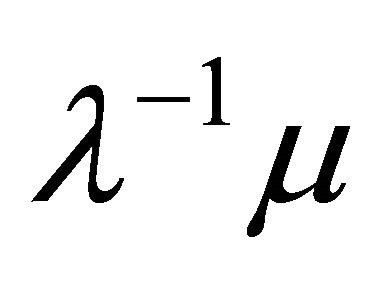 is a primitive
is a primitive  -th root of unity. By the theory of cyclotomic fields (cf. [4-8]),
-th root of unity. By the theory of cyclotomic fields (cf. [4-8]),  is a unique prime ideal
is a unique prime ideal  of B lying above pZ, and
of B lying above pZ, and
 . We have
. We have . Hence
. Hence
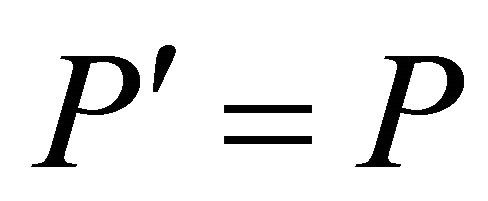 and
and  We have
We have  since
since  . From
. From , we have
, we have 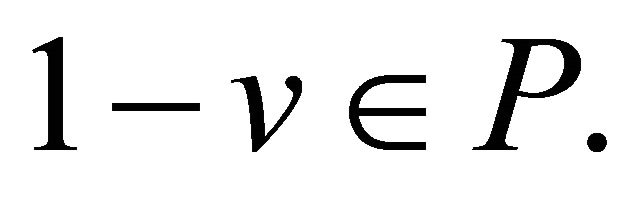 Since
Since  we have
we have  namely,
namely,  This result implies the following. If v is not congruent modulo p to 1, there is no prime ideal J with
This result implies the following. If v is not congruent modulo p to 1, there is no prime ideal J with  and
and  Since
Since

and

the greatest common divisor ideal of 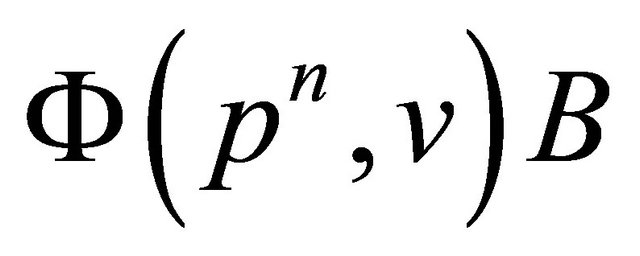 and
and  is B if v is not congruent modulo p to 1. Therefore Case 1 of Theorem 2 is proven.
is B if v is not congruent modulo p to 1. Therefore Case 1 of Theorem 2 is proven.
In Case 2: Let . Let
. Let . Let P denote the unique prime ideal in B lying above pZ, and let
. Let P denote the unique prime ideal in B lying above pZ, and let 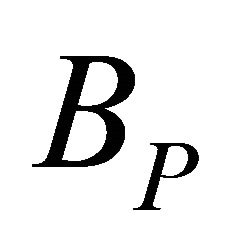 denote the localization of B at P. Let
denote the localization of B at P. Let 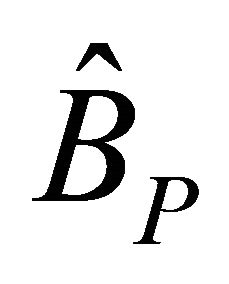 denote the completion of
denote the completion of  with respect to the P-adic (non-Archimedean) absolute value. We use local and global Algebraic Number Theory, cf. [5,9]. We have
with respect to the P-adic (non-Archimedean) absolute value. We use local and global Algebraic Number Theory, cf. [5,9]. We have 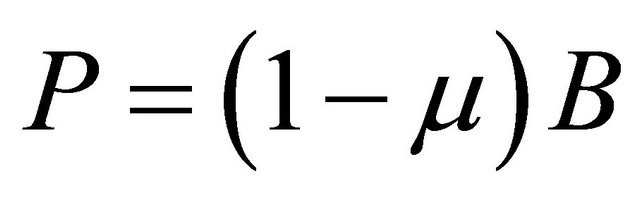 and
and 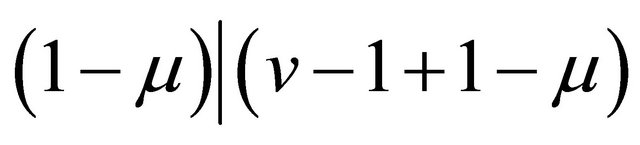 in B. We have
in B. We have
 in
in 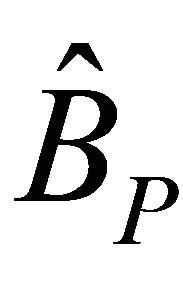 since
since . Hence we get
. Hence we get  using
using 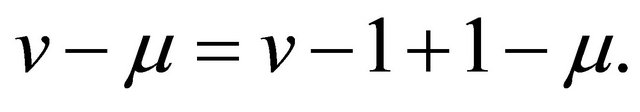 Then we have
Then we have

In the same way we have

using 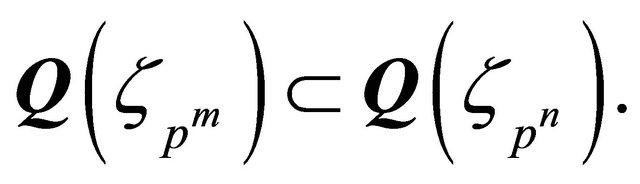 Here we use (1) in Proof 1 above. Therefore we get
Here we use (1) in Proof 1 above. Therefore we get
 if
if . Case 2 of Theorem 2 is proven.
. Case 2 of Theorem 2 is proven.
For each positive integer , let
, let  denote a prime number dividing
denote a prime number dividing  in Case 1 of Theorem 2.
in Case 1 of Theorem 2.
Corollary 2. We have  if
if . There are infinitely many prime numbers.
. There are infinitely many prime numbers.
EXAMPLE of Theorem 2. Let  and let
and let  be a rational integer which is not congruent modulo 5 to 1. Then we have that
be a rational integer which is not congruent modulo 5 to 1. Then we have that  and
and 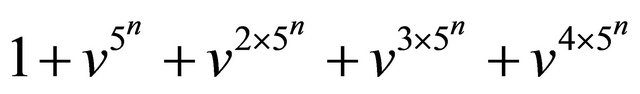 are relatively prime for all rational integers
are relatively prime for all rational integers  and
and  with
with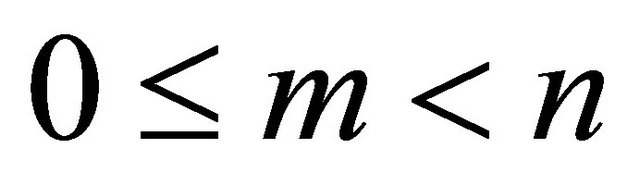 .
.
We give some computations.


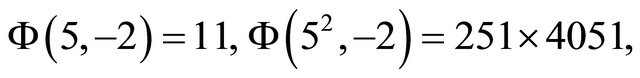

(We used “Scientific WorkPlace”, Version 5.5, MacKichan Software, 19307 8th Avenue NE, Suite C, Poulsbo, WA 98370, USA, for the computations).
Corollary 3 of Theorem 2. Let  be any odd prime number, and let
be any odd prime number, and let  be any rational integer. Then we have the following.
be any rational integer. Then we have the following.
Case 1 that v is not congruent modulo  to
to :
:

for all rational integers  and
and 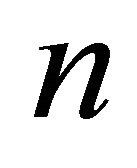 with
with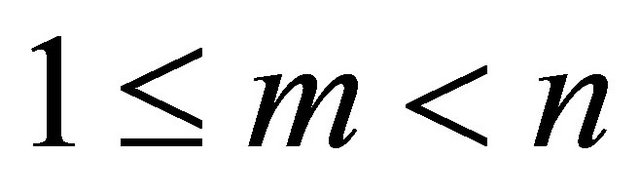 .
.
Case 2 that v is congruent modulo 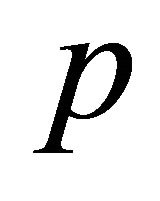 to
to :
:

for all rational integers m and n with .
.
Proof. By ([6], p. 280),  for any positive integer u. Then by Theorem 2, Corollary 3 follows.
for any positive integer u. Then by Theorem 2, Corollary 3 follows.
Corollary 4 of Theorem 2. Let p and q be arbitrary odd prime numbers with , and let
, and let  be any rational integer. Then we have the following.
be any rational integer. Then we have the following.
Case 1 that  is not congruent modulo
is not congruent modulo  to 1:
to 1:

for all rational integers m and n with .
.
Case 2 that  and
and :
:

for all rational integers m and n with .
.
Case 3 that  and that v is not congruent modulo p to 1:
and that v is not congruent modulo p to 1:
We have 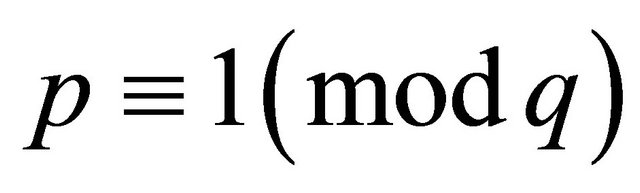 and
and
 or p for all rational integers m and n with
or p for all rational integers m and n with .
.
Proof. From ([6], p. 280) we have
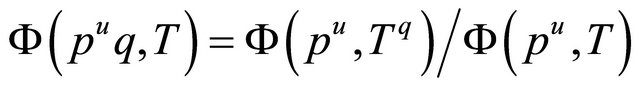
for any positive integer u. Hence

In Case 1, we have

from Theorem 2.
In Case 2: We have

and

from Theorem 2. Hence it follows that
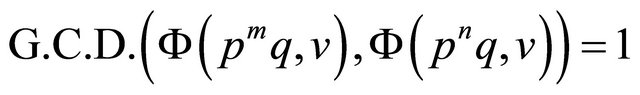 .
.
In Case 3: From , the order of
, the order of  divides q and
divides q and . Since v is not congruent modulo p to 1, the order of
. Since v is not congruent modulo p to 1, the order of  is q. Hence
is q. Hence  From Theorem 2, we have
From Theorem 2, we have

and
 .
.
Here we use

It follows that  or p.
or p.
From Corollary 4 of Theorem 2 we obtain:
Let  and q be arbitrary odd prime numbers with
and q be arbitrary odd prime numbers with , and let
, and let  be any rational integer. If p is not congruent modulo q to 1,
be any rational integer. If p is not congruent modulo q to 1,

for all rational integers m and n with .
.
4. Proof of Exercise IV.3 in [1]
Let us quote the exercise.
Exercise IV.3 in [1]. “If a, m, n are positive integersand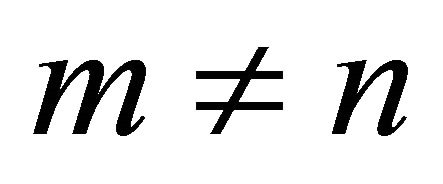 , show that the G.C.D. of
, show that the G.C.D. of  and
and 
is 1 or 2 according as a is even or odd. (Hint. use the fact that  is a multiple of
is a multiple of 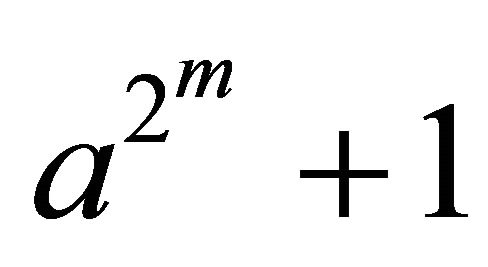 for
for ). From this deduce the existence of infinitely many primes.”
). From this deduce the existence of infinitely many primes.”
We give a proof of this in somewhat generalized form. Namely we show Theorem 3. Let a and b be arbitrary positive rational integers with . Define
. Define  for any positive
for any positive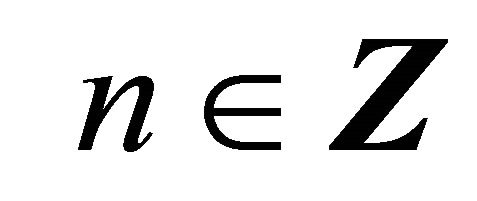 . Let m and n be arbitrary rational integers with
. Let m and n be arbitrary rational integers with . Write
. Write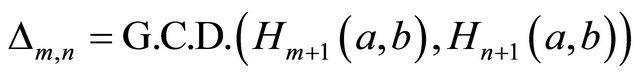 . Then we have:
. Then we have:
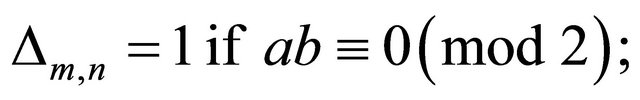

Proof. We have

and
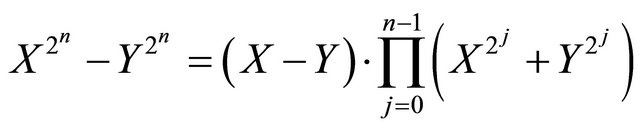 .
.
Hence  for all integers
for all integers . We have also
. We have also

Hence 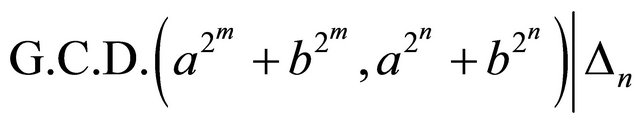 for all integers
for all integers
 . Assume that a prime number p divides
. Assume that a prime number p divides . Then
. Then  does not divide
does not divide 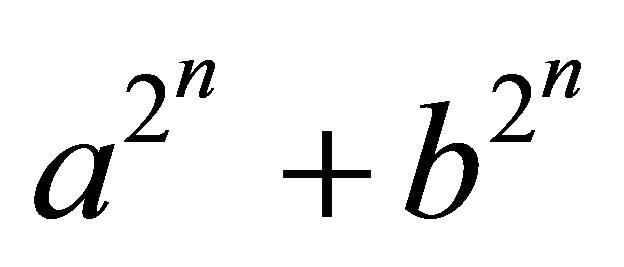 since
since
 . Use
. Use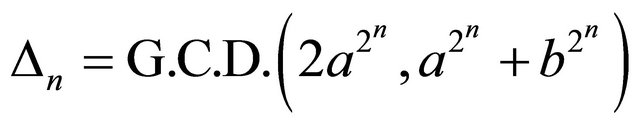 .
.
Therefore . We have
. We have  if
if  is even;
is even;  is even and
is even and  if a and b are odd;
if a and b are odd;  is odd and
is odd and  if a is odd and b is even. Recall
if a is odd and b is even. Recall .
.  if
if  is even.
is even.  if
if
 is odd, since both
is odd, since both  and
and  are even, and
are even, and .
.
Corollary 5 of Theorem 3. Let p be any odd prime number, and let v be any rational integer. Then we have

for all rational integers 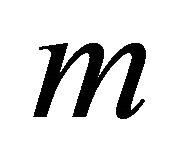 and
and  with
with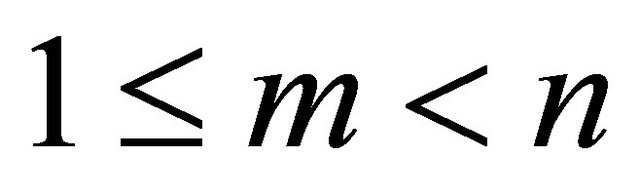 .
.
Proof. By ([6], p. 280),

for any positive integer u. We have 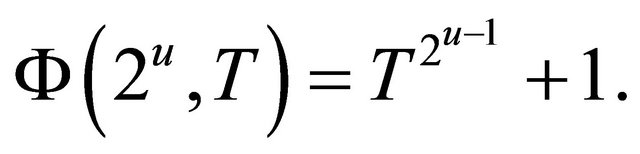 If v is even,
If v is even,

by Theorem 3. If v is odd,

and

by Theorem 3. Then we have Corollary 5 using

In the case of  Corollary 5 is derived also from Theorem 1. For we have
Corollary 5 is derived also from Theorem 1. For we have

5. Acknowledgements
The author concludes that the topic of the present paper relates to Algebraic Number Theory and Theory of Cyclotomic Fields. He would like to thank the referee for valuable suggestions for the important improvement of this paper.