Received 11 February 2015; accepted 26 March 2015; published 30 March 2015

ABSTRACT

Analytical non-perturbative study of the three-dimensional nonlinear stochastic partial differential equation with additive thermal noise, analogous to that proposed by V. N. Nikolaevskii [1] -[5] to describe longitudinal seismic waves, is presented. The equation has a threshold of short-wave instability and symmetry, providing long wave dynamics. New mechanism of quantum chaos generating in nonlinear dynamical systems with infinite number of degrees of freedom is proposed. The hypothesis is said, that physical turbulence could be identified with quantum chaos of considered type. It is shown that the additive thermal noise destabilizes dramatically the ground state of the Nikolaevskii system thus causing it to make a direct transition from a spatially uniform to a turbulent state.

Keywords:

3D Turbulence, Chaos, Quantum Chaos, Additive Thermal Noise, Nikolaevskii System

1. Introduction

In the present work a non-perturbative analytical approach to the studying of problem of quantum chaos in dynamical systems with infinite number of degrees of freedom is proposed. Statistical descriptions of dynamical chaos and investigations of noise effects on chaotic regimes are studied. Proposed approach also allows estimate the influence of additive (thermal) fluctuations on the processes of formation of developed turbulence modes in essentially nonlinear processes like electro-convection and other. A principal role the influence of thermal fluctuations on the dynamics of some types of dissipative systems in the approximate environs of derivation rapid of a short-wave instability was ascertained. Impotent physical results follows from Theorem 2, is illustrated by example of 3D stochastic model system:

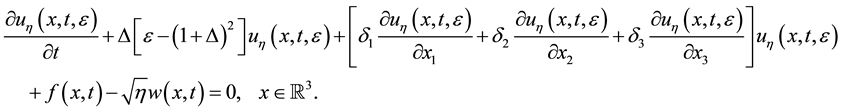(1.1)

, (1.2)

which was obtained from the non-stochastic 3D Nikolaevskii model:

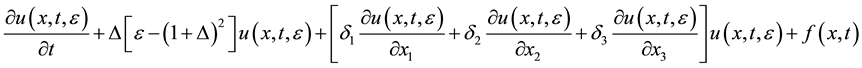(1.3)

which is perturbed by additive “small” white noise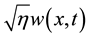. And analytical result also illustrated by example of 1D stochastic model system

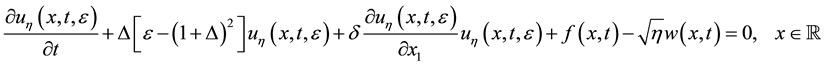(1.4)

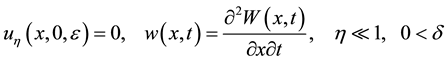(1.5)

which was obtained from the non-stochastic 1D Nikolaevskiis model:

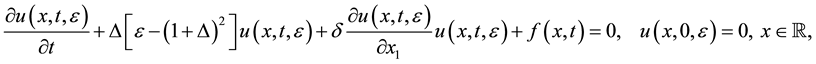(1.6)

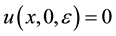. (1.7)

Systematic study of a different type of chaos at onset “soft-mode turbulence” based on numerical integration of the simplest 1D Nikolaevskii model (1.7) has been executed by many authors [2] -[7] . There is an erroneous belief that such numerical integration gives a powerful analysis is means of the processes of turbulence conception, based on the classical theory of chaos of the finite-dimensional classical systems [8] -[11] .

Remark 1.1. However, as it well known, such approximations correct only in a phase of turbulence conception, when relatively small number of the degrees of freedom excites. In general case, when a very large number of the degrees of freedom excites, well known phenomena of the numerically induced chaos, can to spoils in the uncontrollable way any numerical integration [12] -[15] .

Remark 1.2. Other non-trivial problem stays from noise round off error in computer computation using floating point arithmetic [16] -[20] . In any computer simulation the numerical solution is fraught with truncation by round off errors introduced by finite-precision calculation of trajectories of dynamical systems, where round off errors or other noise can introduce new behavior and this problem is a very more pronounced in the case of chaotic dynamical systems, because the trajectories of such systems exhibit extensive dependence on initial conditions. As a result, a small random truncation or round off error, made computational error at any step of computation will tend to be large magnified by future computational of the system [17] .

Remark 1.3. As it well known, if the digitized or rounded quantity is allowed to occupy the nearest of a large number of levels whose smallest separation is E₀, then, provided that the original quantity is large compared to E₀ and is reasonably well behaved, the effect of the quantization or rounding may betreated as additive random noise [18] . Bennett has shown that such additive noise is nearly white, with mean squared value of [19] . However the complete uniform white-noise model to be valid in the sense of weak convergence of probabilistic measures as the lattice step tends to zero if the matrices of realization of the system in the state space satisfy certain nonresonance conditions and the finite-dimensional distributions of the input signal are absolutely continuous [21] [22] .

The method deprived of these essential lacks in general case has been offered by the author in papers [23] - [27] .

Remark 1.4. Thus from consideration above it is clear that numerical integration procedure of the 1D Nikolaevskii model (1.6)-(1.7) executed in papers [2] -[7] in fact dealing with stochastic model (1.4)-(1.5).

There is an erroneous the point of view, that a white noise with enough small intensity does not bring any significant contributions in turbulent modes, see for example [3] . By this wrong assumptions the results of the numerical integration procedure of the 1D Nikolaevskii model (1.6)-(1.7) were mistakenly considered and interpreted as a very exact modeling the slow turbulence within purely non stochastic Nikolaevskii model (1.6)-(1.7). Accordingly wrong conclusions about that temperature noises does not influence slow turbulence have been proposed in [3] . However, in [27] has shown non-perturbatively that a white noise with enough small intensity can to bring significant contributions in turbulent modes and even to change this modes dramatically.

At the present time it is generally recognized that turbulence in its developed phase has essentially singular spatially-temporal structure. Such as in gular conduct is impossible to describe adequately by the means of some model system of equations of a finite dimensionality. In this point a classical theory of chaos is able to describe only small part of turbulence phenomenon in liquid and another analogous of dynamical systems. The results of non-perturbative modeling of super-chaotic modes, obtained in the present paper allow us to put out a quite probable hypothesis: developed turbulence in the real physical systems with infinite number of degrees of freedom is a quantum super-chaos, at that the quantitative characteristics of this super-chaos, is completely determined by non-perturbative contribution of additive (thermal) fluctuations in the corresponding classical system dynamics [18] -[20] .

2. Main Theoretical Results

We study the stochastic r-dimensional differential equation analogous proposed by Nikolaevskii [1] to describe longitudinal seismic waves:

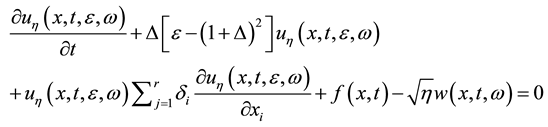(2.1)

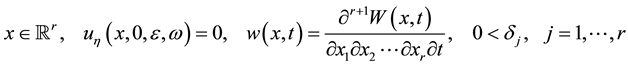(2.2)

The main difficulty with the stochastic Nikolaevskii equation is that the solutions do not take values in a function space but in generalized function space. Thus it is necessary to give meaning to the non-linear terms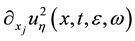, 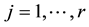because the usual product makes no sense for arbitrary distributions. We deal with product of distributions via regularizations, i.e., we approximate the distributions by appropriate way and pass to the limit. In this paper we use the approximation of the distributions by approach of Colombeau generalized func- tions [28] .

Notation 2.1.We denote by 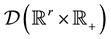the space of the infinitely differentiable functions with compact supportin 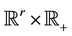and by its dual space. Let be a probability space. We denote by D the space of all functions such that is a random variable for all . The elements of D are called random generalized functions.

Definition 2.1. [29] . We say that a random field is a spatially dependent semimartingale if for each is a semimartingale in relation to the same filtration. If is a -function of x and continuous in almost everywhere, it is called a -semimartingale.

Definition 2.2. We say that that is a strong generalized solution (SGS) of Equations (2.1)- (2.2) if there exists as equence of -semimartingales such that there exists

1) in almost surely for,

2) almost surely for,

3) for all,

4)

5) almost surely for.

However, in this paper we use the solutions of stochastic Nikolaevskii equation only in the sense of Colombeau generalized functions [30] .

Remark 2.1. Note that from Definition 2.2 it is clear that any strong generalized solution of Equations (2.1)-(2.2) one can to recognized as Colombeau generalized function such that

By formula (#) one can to define appropriate generalized solution of Equations (2.1)-(2.2) even if a strong generalized solution of Equations (2.1)-(2.2) does not exist.

Definition 2.3. Assume that a strong generalized solution of Equations (2.1)-(2.2) does not exist. We shall say that:

1) Colombeau generalized stochastic process is a weak generalized solution (WGS) of Equations (2.1)-(2.2) or Colombeau solution of Equations (2.1)-(2.2) if for all and for all

a)

b) almost surely for.

2) Colombeau generalized stochastic process is a Colombeau-Ito’s solution of Equations (2.1)-(2.2) if for all and for all

a)

b) almost surely for.

Notation 2.2. [30] . The algebra of moderate element we denote by. The Colombeau algebra of the Colombeau generalized function we denote by.

Notation 2.3. [30] . We shall use the following designations. If it representatives will be denoted by R_U, their values on, will be denoted by and it point values at will be denoted.

Definition 2.4. [30] . Let be the set of all such that.

Let be a probability space. Colombeau random generalized function this is a map such that there is representing function with the properties:

1) for fixed the function is a jointly measurable on;

2) almost surely in, the function belongs to and is a representative of U;

Notation 2.3. [30] . The Colombeau algebra of Colombeau random generalized function is denoted by.

Definition 2.5. Let be a probability space. Classically, a generalized stochastic process on is a weakly measurable map denoted by. If, then

3) is a measurable with respect to and

4) Smooth with respect to and hence jointly measurable.

5) Also.

6) Therefore qualifies as an representing function for an element of.

7) In this way we have an imbedding.

Definition 2.6. Denote by the space of rapidly decreasing smooth functions on. Let with 1), 2) S-the Borel σ-algebra generated by the weak topology. Therefore there is unique probability measure on such that

for all. White noise with the support in T is the generalized process

such that: 1), 2), 3).

Viewed as a Colombeau random generalized function, it has a representative (denoting on variables in by):, which vanishes if t is less than minus the diameter of the support of. Therefore is a zero on in. Note that its variance is the Colombeau constant:

Definition 2.7. Smoothed with respect to white noise the representative with

, such that, and.

Theorem 2.1. [25] . (Large Deviation Principle for SPDE) (I) Let, be solution of the Colombeau-Ito’s SPDE [26] :

(2.3)

(2.4)

Here: 1) the Colombeau algebra of Colombeau generalized functions and.

2)

3) is a smoothed with respect to white noise.

(II) Let, be solution of the Colombeau-Ito’s SDE [26] :

(2.5)

(2.6)

(2.7)

Here Equations (2.5)-(2.7) is obtained from Equations (2.3)-(2.4) by spatial discretization on finite lattice if and is a latticed Laplacian [31] -[33] .

(III) Assume that Colombeau-Ito’s SDE (2.5)-(2.7) is a strongly dissipative [26] .

(IV) Let be the solutions of the linear PDE:

(2.8)

. (2.9)

Then

(2.10)

Proof. The proof based on Strong Large Deviations Principles (SLDP-Theorem) for Colombeau-Ito’s solution of the Colombeau-Ito’s SDE, see [26] , Theorem 6. By SLDP-Theorem one obtain directly the differential master equation (see [26] , Equation (90)) for Colombeau-Ito’s SDE (2.5)-(2.7):

(2.11)

(2.12)

We set now Then from Equations (2.11)-(2.12) we obtain

(2.13)

(2.14)

From Equations (2.5)-(2.7) and Equations (2.13)-(2.14) by SLDP-Theorem (see see [26] , inequality (89)) we obtain the inequality

(2.15)

Let us consider now the identity

(2.16)

From the identity (2.16) by integration we obtain the identity

(2.17)

From the identity (2.17) by using the triangle inequality we obtain the inequality

(2.18)

From the inequality (2.18) by the inequality (2.15) for all we obtain the inequality

(2.19)

In the limit from the inequality (2.19) we obtain the inequality

In the limit from the inequality we obtain the inequality

(2.20)

We note that

(2.21)

Therefore from (2.20) and (2.21) we obtain the inequality

(2.22)

In the limit from Equations (2.13)-(2.14) for any fixed, , we obtain the differential master equation for Colombeau-Ito’s SPDE (2.3)-(2.4)

(2.23)

(2.24)

Therefore from the inequality (2.22) follows the inequality

(2.25)

In the limit from differential Equations (2.23)-(2.24) we obtain the differential Equations (2.8)-(2.9) and it is easy to see that

(2.26)

From the inequality (2.25) one obtain the inequality

(2.27)

From the inequality (2.27) and Equation (2.26) finally we obtain the inequality

(2.28)

The inequality (2.28) finalized the proof.

Definition 2.7. (The Differential Master Equation) The linear PDE:

(2.29)

(2.30)

we will call as the differential master equation.

Definition 2.8. (The Transcendental Master Equation) The transcendental equation

(2.31)

we will call as the transcendental master equation.

Remark 2.2. We note that concrete structure of the Nikolaevskii chaos is determined by the solutions variety by transcendental master Equation (2.31). Master Equation (2.31) is determines by the only way some many-valued function which is the main constructive object, determining the characteristics of quantum chaos in the corresponding model of Euclidian quantum field theory.

3. Criterion of the Existence Quantum Chaos in Euclidian Quantum N-Model

Definition 3.1. Let be the solution of Equation (2.1). Assume that for almost all points (in the sense of Lebesgue-measureon), there exist a function such that

(3.1)

Then we will say that a function is a quasi-determined solution (QD-solution of Equation (2.1)).

Definition 3.2. Assume that there exist a set that is positive Lebesgue-measure, i.e., and

(3.2)

i.e., imply that the limit: does not exist.

Then we will say that Euclidian quantum N-model has the quasi-determined Euclidian quantum chaos (QD- quantum chaos).

Definition 3.3. For each point we define a set by the condition:

(3.3)

Definition 3.4. Assume that Euclidian quantum N-model (2.1) has the Euclidian QD-quantum chaos.

For each point we define a set-valued function by the condition:

(3.4)

We will say that the set-valued function is a quasi-determined chaotic solution (QD-chaotic solution) of the quantum N-model (In Figure 1 and Figure 2).

Theorem 3.1. Assume that Then for all values of parameters such that, , , , , quantum N-model (2.1) has the QD- chaotic solutions.

Definition 3.5. For each point we define the functions such that:

1)

2)

3)

Definition 3.7.

1) Function is called upper bound of the QD-quantum chaos at point

2) Function is called lower bound of the QD-quantum chaos at point

3) Function is called width of the QD-quantum chaos at point.

Definition 3.8. Assume now that

(3.5)

Then we will say that Euclidian quantum N-model has QD-quantum chaos of the asymptotically finite width at point.

Definition 3.9. Assume now that

(3.6)

Then we will say that Euclidian quantum N-model has QD-quantum chaos of the asymptotically infinite width at point (in Figure 3, Figure 4)

Definition 3.10. For each point we define the functions such that:

1)

2)

3)

Theorem 3.2. For each point is satisfied the inequality

(3.7)

Proof. Immediately follows by Theorem 2.1 and Definitions 3.5, 3.10.

Theorem 3.3. (Criterion of QD-quantum chaos in Euclidian quantum N-model)

Assume that

(3.8)

Then Euclidian quantum N-model has QD-quantum chaos.

Proof. Immediately follows by the Inequality (3.7) and Definition 3.2.

4. Quasi-Determined Quantum Chaos and Physical Turbulence Nature

In generally accepted at the present time hypothesis what physical turbulence in the dynamical systems with an infinite number of degrees of freedom really is, the physical turbulence is associated with a strange attractors, on which the phase trajectories of dynamical system reveal the known properties of stochasticity: a very high dependence on the initial conditions, which is associated with exponential dispersion of the initially close trajectories and brings to their non-reproduction; everywhere the density on the attractor almost of all the trajectories a very fast decrease of local auto-correlation function [2] -[9]

(4.1)

Here

In contrast with canonical numerical simulation, by using Theorem 2.1 it is possible to study non-perturba- tively the influence of thermal additive fluctuations on classical dynamics, which in the considered case is described by Equation (4.1).

The physical nature of quasi-determined chaos is simple and mathematically is associated with discontinuously of the trajectories of the stochastic process on parameter.

In order to obtain the characteristics of this turbulence, which is a very similarly to local auto-correlation function (3.1) we define bellow some appropriate functions.

Definition 4.1. The numbering function of quantum chaos in Euclidian quantum N-model is defined by

(4.2)

Here by we denote the cardinality of a finite set X, i.e., the number of its elements.

Definition 4.2. Assume now that a set is ordered be increased of its elements. We introduce the function, which value at point, equals the i-th element of a set.

Definition 3.3. The mean value function of the chaotic solution at point is defined by

(4.3)

Definition 3.4. The turbulent pulsations function of the chaotic solution at point is defined by

(4.4)

Definition 3.5. The local auto-correlation function is defined by

(4.5)

(4.6)

Definition 3.6. The normalized local auto-correlation function is defined by

(4.7)

Let us consider now 1D Euclidian quantum N-model corresponding to classical dynamics

(4.8)

Corresponding Langevin equation are [34] [35] :

(4.9)

(4.10)

Corresponding differential master Equations (2.29)-(2.30) are

(4.11)

. (4.12)

Corresponding transcendental master Equation (2.31) are

(4.13)

(4.14)

We assume now that. Then from Equation (4.13) for all we obtain

, or (4.14)

(4.15)

The result of calculation using transcendental master Equation (4.15) the corresponding function is presented by Figure 5 and Figure 6.

The result of calculation using master Equation (4.13) the corresponding function is presented by Figure 7 and Figure 8.

Let us calculate now corresponding normalized local auto-correlation function. The result of calculation using Equation (4.7) is presented by Figure 9 and Figure 10.

In paper [7] the mechanism of the onset of chaos and its relationship to the characteristics of the spiral attractors are demonstrated for inhomogeneous media that can be modeled by the Ginzburg-Landau Equation (4.14). Numerical data are compared with experimental results (in Figure 11).

(4.14)

However, as pointed out above (see Remarks 1.1-1.4) such numerical simulation in fact gives numerical data for stochastic model

(4.15)

5. The Order of the Phase Transition from a Spatially Uniform State to a Turbulent State at Instant

In order to obtain the character of the phase transition (first-order or second-order on parameters) from a spatially uniform to a turbulent state at instant one can to use the transcendental master Equation (2.31) of the form

(5.1)

By differentiation Equation (5.1) one obtain

(5.2)

From Equation (5.2) one obtain

(5.3)

Let us consider now 1D Euclidian quantum N-model given by Equations (4.9)-(4.10). From corresponding transcendental master Equation (4.13) by differentiation Equation (4.13) with respect to variable one obtain

(5.4)

From Equation (5.4) for a sufficiently small one obtain

. (5.5)

From master Equation (4.13) one obtain by differentiation Equation (4.13) with respect to variable one obtain

(5.6)

From Equation (5.6) for a sufficiently small one obtain

(5.7)

Therefore from Equation (5.3), (5.5) and (5.7) one obtain

(5.8)

In the from Equation (5.8) one obtain

(5.9)

and where

.

From Equation (5.9) follows that

(5.10)

. (5.11)

From Equations (5.10)-(5.11) follows second order discontinuity of the quantity at instant. Therefore the system causing it to make a direct transition from a spatially uniform state to a turbulent state in an analogous fashion to the second-order phase transition in quasi-equilibrium systems.

6. Chaotic Regime Generated by Periodical Multi-Modes External Perturbation

Assume now that external periodical force has the following multi-modes form (Figure 12)

(6.1)

Corresponding transcendental master equation are (Figure 13)

(6.2)

Let us consider the examples of QD-chaotic solutions with a periodical force (Figure 14):

(6.3)

7. Conclusion

A non-perturbative analytical approach to the studying of problem of quantum chaos in dynamical systems with infinite number of degrees of freedom is proposed and developed successfully. It is shown that the additive thermal noise destabilizes dramatically the ground state of the system thus causing it to make a direct transition from a spatially uniform to a turbulent state.

Acknowledgements

A reviewer provided important clarifications.

Cite this paper

Jaykov Foukzon,, (2015) New Scenario for Transition to Slow 3-D Turbulence. Journal of Applied Mathematics and Physics, 03, 371-389. doi: 10.4236/jamp.2015.33048

References