ABSTRACT

In this work we describe a reconstruction algorithm for zero-order hold (ZOH) waveforms measured by a parallel sampling scheme. In the method the ZOH signal is fed to a parallel network consisting of resistor-capacitor (RC) filters, whose outputs are sampled simultaneously. The algorithm reconstructs N previous samples of the input signal from output samples of N parallel RC circuits. The method is especially useful in sampling and reconstruction of the ZOH signals produced by the digital-to-analog converters. Using the parallel sampling method the sampling rate of the analog-to-digital converters can be increased by a factor of N. We discuss a variety of applications such as reconstruction of ZOH pulse sequences produced by ultra wide band (UWB) transmitters.

1. Introduction

The present sampling methods are based on the Shannon’s famous theorem [1], which concerns the sampling of the band-limited signals at equidistant time intervals. However, for example the measurement of ultra wide band (UWB) pulses gives rise to an extended demand for the signal sampling devices. The analog-to-digital converters (ADCs) have a limited conversion time, which is not sufficient for sampling of the short term transients. In signal processing society the sequential sampling scheme based on the finite rate of innovation (FRI) has been an object of active interest for reconstruction of the UWB pulses and other discontinuities [2-6]. In FRI methods the transient signal is fed to an analogue network, which broadens the signal for sampling with an ADC. The reconstruction algorithm is based on the ad hoc knowledge of the signal waveform. In our previous work [7] we introduced a new method for sampling and reconstruction of continuous transient waveforms. The signal is fed to the parallel network consisting resistor-capacitor (RC) filters. The outputs of the RC filters are sampled simultaneously. N signal samples can be reconstructed from the single samples of N parallel RC circuits. The reconstruction algorithm was based on the replacement of the convolution integral by the Riemann sum. Recently we observed that in reconstruction of transient pulse sequences, the Riemann sum is too rough estimate for the convolution integral. Especially when the signal is produced by the digital-to-analog converter (DAC), the reconstruction of the ZOH (piecewise constant) signal may involve unpredictable errors. In the following we present an algorithm for computation of the convolution integral. We describe the parallel RC network, develop the reconstruction algorithm and describe potential applications of the parallel sampling scheme.

2. Parallel Sampling Scheme for ZOH Signals

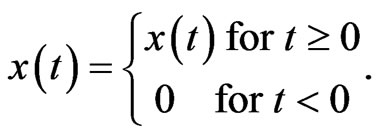(1)

The signal is fed to the network consisting of N parallel RC filters shown in Figure 1. The exponential impulse responses of the RC filters are for

(2)

where and C is the scaling constant. For the RC filter outputs, which are sampled simultaneously

at time the following is valid

(3)

where * denotes convolution and the dummy integration variable. For computation of (3) the measurement instant is divided to N equal intervals. The discrete samples of the measurement signal are denoted by and the outputs of the RC filters by. Supposing that the measurement signal is a ZOH signal yieded by DAC with a frequency the convolution (3) can be integrated on intervals. We have

(4)

Using the short notation we obtain

(5)

which yields  the following matrix/vector representation

(6)

Equation (6) includes a non-singular Vandermonde matrix having rank. This enables us to solve the input signal, , from the outputs of N parallel RC filters, sampled at the time instant. The signal vector x, containing N discrete values, can be reconstructed from

(7)

Since the inverse matrix depends only on the properties of RC filters and the discretization interval, the signal reconstruction in later measurements is obtained by a single matrix-vector multiplication with the previously computed.

The above formulation is relevant only for the reconstruction of the N consecutive samples from the causal ZOH pulse sequence. For measurement of the next sequence of N samples, the parallel RC network was modified by adding a FET switch and a sample and hold (S/H) circuit (Figure 2). The switch resets the output at the beginning of the measurement period at the time instant and the S/H circuit samples the signal at. The next measurement period follows the same procedure. With this arrangement the ZOH waveform can be reconstructed without discontinuities.

The theoretical validation of the reconstruction algorithm (6,7) was tested by simulating the parallel RC network (Figure 1) via the analog electronic circuit simulator (Spice). In the absence of noise the reconstruction algorithm recovered the ZOH waveforms with machine precision. When the random noise was added to the ZOH signal, the RC filters reduced clearly the noise level in the outputs. In the presence of noise the reconstruction produced ZOH signal levels, which matched the time averaged values

(8)

3. Experiments and Results

The measurement equipment consisted of eight parallel RC-circuits equipped with FET switches and sample and hold (S/H) circuits. The parameter varied in the range 0.1, , 0.7. The outputs of the S/Hs were fed to the differential eight channel 12 bit ADC unit, hich had the +/–5 V measurement range. Using this arrangement eight ZOH signal samples were reconstructed corresponding to the measurement interval.

The piecewise constant test signals were produced by eight bit DAC, whose output was equipped with a unit gain buffer amplifier. The DAC pulse frequency varied between 10 kHz and 1 MHz. All experimental tests were performed in a Faraday gage.

The ZOH pulse sequences comprised of sinusoidal, damped sinusoidal and various types of pulse waveforms. In all cases the algorithm reconstructed the ZOH signals with an average error being typically in the range 3.5 - 4.2 mV. Most of the error was related to the quantization noise of the ADC unit.

4. Discussion and Conclusions

In our earlier work [7] we described a new measurement and sampling concept, which permits the reconstruction of short term transient signals. The key idea was the use of the parallel RC filters, whose outputs are measured simultaneously. The reconstruction algorithm was based on the replacement of the convolution integral (3) by the Riemann sum. In this work we reformulated the reconstruction algorithm for the ZOH waveforms. The key idea is that since the ZOH signal is convolved with the impulse response of the RC filter, the convolution integral can be calculated analytically integrating on intervals.

In our previous work we calibrated the measurements by denoting the impulse response of the RC circuit as

(9)

We wrote in [7] “In an ideal case, , but in practise they may slightly differ from each other”. To obtain relevant results each of the values were independently calibrated. The Riemann sum reconstruction method yielded the following result

(10)

It is interesting that for small values we may take two terms of the series expansion in (6). By equalizing, we obtain

(11)

i.e. series approximation reduces (5) to that yielded by Riemann sum (10). However, in most cases the series approximation is too rough for ZOH signals. The scaling constant C affects the gain of the different channels and only one calibration coefficient is needed to calibrate all channels in parallel RC network.

In the present parallel sampling scheme the simultaneous measurements at the outputs of the RC filters are taken at intervals. During that period the ZOH signal has N transitions. The role of the RC network is to work as a low-pass filter by smoothing the abrupt changes of the pulse edges and filtering the random noise.

The reconstruction of the N signal samples needs only one matrix-vector multiplication (7). The analytical formulae for the inversion of the Vandermonde matrix in (6) are well known [8-13]. The explicit solutions are preferred since they are more accurate than the general matrix inversion algorithms.

The conversion time of the ADCs is limited to the through output time of the comparator chain. In VLSI design the most effective configuration would be to use individual ADCs equipped with a S/H circuits to measure the parallel RC filters separately. By using N parallel RC filter network the conversion time of each ADC can be prolonged to. This makes it possible to increase the sampling rate of the data acquisition system by a factor of N.

In test measurements we found only a tiny interference due to the operation of the FET switches. Obviously the RC filters effectively reduce most of the high frequency noise imposed on the signal.

The present method has plenty of applications including the measurement of pulse trains yielded by pulse lasers and ultra wide-band (UWB) pulse transmitters. Usually the UWB pulses are short transients and the information is coded to the appearance time of the pulses. The information may also be coded to the shape of the UWB pulses [14]. Using a single receiver several transmitters can be measured simultaneously e.g. in multisensor applications.

The present parallel sampling scheme can be seen as a special case of the setup called sparse or compressive sampling [15-20], which can be adapted to recover certain signals from far fewer measurements than conventional sampling methods require.

5. Acknowledgements

We are indebted to the anonymous referee for comments, which have improved the manuscript significantly.

REFERENCES

NOTES

This work was supported by the National Technology Agency of Finland (TEKES).