Journal of Applied Mathematics and Physics
Vol.2 No.7(2014), Article
ID:47035,14
pages
DOI:10.4236/jamp.2014.27075
Lie Symmetries, One-Dimensional Optimal System and Optimal Reduction of (2 + 1)-Coupled nonlinear Schrödinger Equations
A. Li1, Chaolu Temuer2
1Inner Mongolia University, Hohhot, China
2Shanghai Maritime University, Shanghai, China
Email: 342388241@qq.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 March 2014; revised 27 April 2014; accepted 7 May 2014
Abstract
For a class of (1 + 2)-dimensional nonlinear Schrödinger equations, the infinite dimensional Lie algebra of the classical symmetry group is found and the one-dimensional optimal system of an 8-dimensional subalgebra of the infinite Lie algebra is constructed. The reduced equations of the equations with respect to the optimal system are derived. Furthermore, the one-dimensional optimal systems of the Lie algebra admitted by the reduced equations are also constructed. Consequently, the classification of the twice optimal symmetry reductions of the equations with respect to the optimal systems is presented. The reductions show that the (1 + 2)-dimensional nonlinear Schrödinger equations can be reduced to a group of ordinary differential equations which is useful for solving the related problems of the equations.
Keywords:Nonlinear Schrödinger Equations, Lie Aymmetry Group, Lie algebra, Optimal System

1. Introduction
We plan to consider the (1 + 2)-dimensional coupled nonlinear Schrödinger (2D-CNLS) equations with cubic nonlinearity
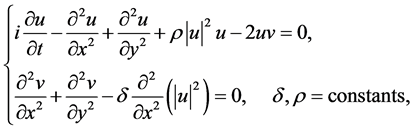 (1)
(1)
where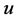 ,
,  are complex-valued functions. The 2D-CNLS equations which describes the evolution of the wave packet on a two-dimensional water surface under gravity was derived by Benny and Roskes [1] and Davey and Stewartson [2] . The solutions of the equation have been studied by several authors [3] -[12] . The multisoliton solutions were obtained by Anker and Freeman [8] . They showed that the two-soliton resonant interaction occurs and a triple soliton structure is produced. A similarity reductions of the 2D-CNLS equation is also studied in [9] . Nakamura [10] found explode-decay mode solutions by using the bilinear method. However, the algebra properties of the Lie algebra admitted by (1) has not been studied so far. The optimal system of the Lie algebra yields the optimal classification of the invariant solutions set to the 2D-CNLS which is essential to distinguish the inequivalent classes of the invariant solutions of the equation.
are complex-valued functions. The 2D-CNLS equations which describes the evolution of the wave packet on a two-dimensional water surface under gravity was derived by Benny and Roskes [1] and Davey and Stewartson [2] . The solutions of the equation have been studied by several authors [3] -[12] . The multisoliton solutions were obtained by Anker and Freeman [8] . They showed that the two-soliton resonant interaction occurs and a triple soliton structure is produced. A similarity reductions of the 2D-CNLS equation is also studied in [9] . Nakamura [10] found explode-decay mode solutions by using the bilinear method. However, the algebra properties of the Lie algebra admitted by (1) has not been studied so far. The optimal system of the Lie algebra yields the optimal classification of the invariant solutions set to the 2D-CNLS which is essential to distinguish the inequivalent classes of the invariant solutions of the equation.
In this paper, we show the optimal reduction classifications of the 2D-CNLS equations (1) through studying one-dimensional optimal system of the Lie algebra of the equations.
Outline of the paper is following. In §2, the complete infinite-dimensional Lie algebra  of the Lie symmetry group of the 2D-CNLS equations is derived which covered the results obtained in [9] . In §3, the onedimensional optimal system of an 8-dimensional subalgebra
of the Lie symmetry group of the 2D-CNLS equations is derived which covered the results obtained in [9] . In §3, the onedimensional optimal system of an 8-dimensional subalgebra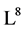 , presented in [9] , of the
, presented in [9] , of the 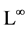 is constructed. In §4 the first reductions of the 2D-CNLS equation (1) with respect to the optimal system obtained in §3 are given. In §5 we construct one-dimensional optimal systems of Lie algebras of the reduced equations obtained in §4 which yields the second reductions of (1). Consequently, the 2D-CNLS equation (1) can be reduced to a group of scale ordinary differential equations, which is essential to solve different exact solutions of the 2D-NLS equation (1).
is constructed. In §4 the first reductions of the 2D-CNLS equation (1) with respect to the optimal system obtained in §3 are given. In §5 we construct one-dimensional optimal systems of Lie algebras of the reduced equations obtained in §4 which yields the second reductions of (1). Consequently, the 2D-CNLS equation (1) can be reduced to a group of scale ordinary differential equations, which is essential to solve different exact solutions of the 2D-NLS equation (1).
2. The Lie Algebra of the 2D-CNLS Equations (1)
In this section, we present the Lie algebra of point symmetries of 2D-CNLS (1). To obtain the Lie algebra, we consider the one parameter Lie symmetry group of infinitesimal transformations in 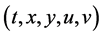 given by
given by
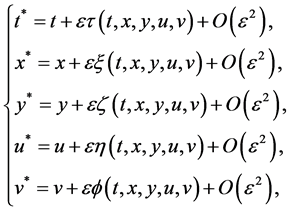 (2)
(2)
where  is the group parameter. Hence the corresponding generator of the Lie algebra of the symmetry group is
is the group parameter. Hence the corresponding generator of the Lie algebra of the symmetry group is

Transforming 2D-CNLS equations (1) to real case by transformations 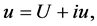
 , where
, where ,
, 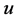 ,
,  and
and  are real functions, one has real form of the 2D-CNLS equations (1) in four unknown functions
are real functions, one has real form of the 2D-CNLS equations (1) in four unknown functions 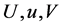 and
and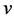 .
.
Assuming that the 2D-CNLS equations (1) is invariant under the transformations (2), then its real form transformed system is invariant under the Lie symmetry group with generator
 , in which
, in which 
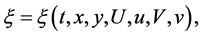

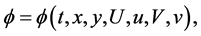

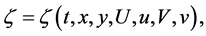
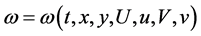 . By invariance criterion in [11] -[13] , we have the DTEs of the Lie symmetry group as follows
. By invariance criterion in [11] -[13] , we have the DTEs of the Lie symmetry group as follows
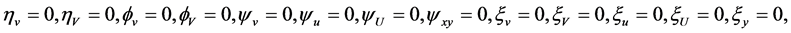


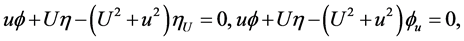




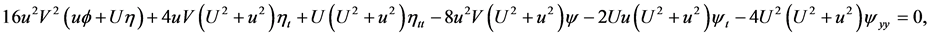

for functions . Solving this system by characteristic set algorithm given in [14] [15] , we obtain the infinitesimal functions of generator
. Solving this system by characteristic set algorithm given in [14] [15] , we obtain the infinitesimal functions of generator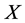 , i.e.,
, i.e.,
 (3)
(3)
where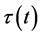 ,
,  ,
, 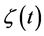 ,
, 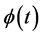 are arbitrary functions of their argument. Hence the 2D-CNLS (1) admits infinite dimensional Lie algebra
are arbitrary functions of their argument. Hence the 2D-CNLS (1) admits infinite dimensional Lie algebra . It is notice that in [9] only a special subset of (3) were found. Namely, if taking here a linear independent representatives of the vectors
. It is notice that in [9] only a special subset of (3) were found. Namely, if taking here a linear independent representatives of the vectors 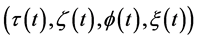 as
as
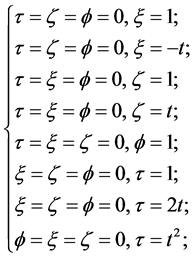
respectively and by transforming 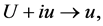
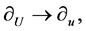


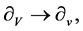
 , we recover the basis of the 8-dimensional Lie algebra
, we recover the basis of the 8-dimensional Lie algebra  given in [9] as follows
given in [9] as follows
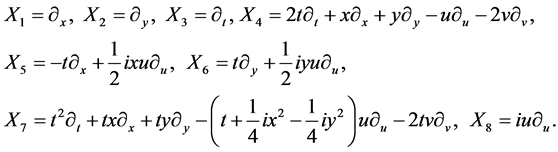 (4)
(4)
If taking other linear independents case of vector , we obtain other subalgebras of
, we obtain other subalgebras of
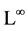 . In this paper, we take the case (4) as example to show the investigation procedure for finite sub-algebras properties of the infinite dimensional algebra
. In this paper, we take the case (4) as example to show the investigation procedure for finite sub-algebras properties of the infinite dimensional algebra .
.
The commutators of the generators (4) are given in the Table 1, where the entry in the  row and
row and 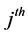
column is defined as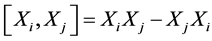 ,
, 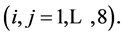
The table is fundamental for our constructing the optimal system of the 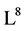 with basis (4).
with basis (4).
3. One-Dimensional Optimal System of (8
In this section, we give an one-dimensional optimal system of the Lie algebra  spaned by (4). Finding one-dimensional optimal system of one-dimensional subalgebras of a Lie algebra is a subalgebra classification problem. It is essentially the same as the problem of classifying the orbit of the adjoint representation, since each one-dimensional subalgebra is determined by nonzero vector in the Lie algebra. Hence it is equivalent to classification of subalgebras under the adjoint representation of the Lie algebra. The adjoint representation is given by the Lie series
spaned by (4). Finding one-dimensional optimal system of one-dimensional subalgebras of a Lie algebra is a subalgebra classification problem. It is essentially the same as the problem of classifying the orbit of the adjoint representation, since each one-dimensional subalgebra is determined by nonzero vector in the Lie algebra. Hence it is equivalent to classification of subalgebras under the adjoint representation of the Lie algebra. The adjoint representation is given by the Lie series

where 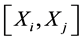 is the commutator given in Table 1,
is the commutator given in Table 1, 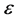 is a parameter, and
is a parameter, and . This yields following adjoint commutator Table 2 for (4) in which the
. This yields following adjoint commutator Table 2 for (4) in which the 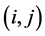 entry gives
entry gives .
.
The following is the deduction procedure of one-dimensional optimal system of (4) by using the method given in [15] -[20] .
Let 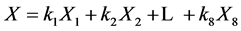 be an element of
be an element of  spanned by (4), which we shall try to simplify using suitable adjoint maps and find its equivalent representative. A key observation here is that the function
spanned by (4), which we shall try to simplify using suitable adjoint maps and find its equivalent representative. A key observation here is that the function
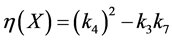 is an invariant of the full adjoint action, that means
is an invariant of the full adjoint action, that means 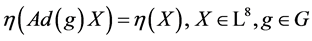
(the corresponding symmetry group of the Lie algebra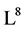 ). The detection of such an invariant is important since it places restrictions on how far we can expect to simplify
). The detection of such an invariant is important since it places restrictions on how far we can expect to simplify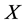 . For example, if
. For example, if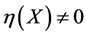 , then we cannot simultaneously make
, then we cannot simultaneously make  and
and 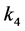 all zero through adjoint maps; if
all zero through adjoint maps; if , we cannot make either
, we cannot make either 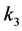
or 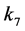 zero!
zero!
To begin the classification process, we first concentrate on the coefficients  of
of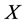 . Acting simultaneously adjoints of
. Acting simultaneously adjoints of 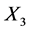 and
and , one has
, one has
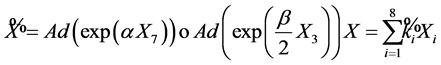
with coefficients
 (5)
(5)
Table 1. The commutators of (4).
Table 2. The adjoint commutator of (4).
There are now three cases, depending on the sign of the invariant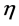 .
.
Case 1. If , then we choose
, then we choose 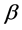 to be either real root of the quadratic equation
to be either real root of the quadratic equation
 and
and 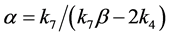 (which is always well defined). Then
(which is always well defined). Then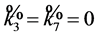 , while
, while
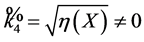 , so
, so 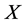 is equivalent to a multiple of
is equivalent to a multiple of . Acting further by adjoint maps generated respectively by
. Acting further by adjoint maps generated respectively by 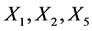 and
and  we can arrange that the coefficients of
we can arrange that the coefficients of
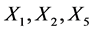 and
and  in
in  vanish. Therefore, every element
vanish. Therefore, every element  with
with 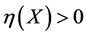 is equivalent to a multiple of
is equivalent to a multiple of 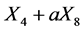 for some
for some . No further simplifications are possible.
. No further simplifications are possible.
Case 2. If 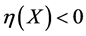 (implies
(implies ), set
), set  to make
to make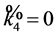 . Acting on
. Acting on  by the group generated by
by the group generated by , we can make the coefficients of
, we can make the coefficients of 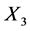 and
and  agree, so
agree, so 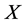 is equivalent to a scalar multiple of
is equivalent to a scalar multiple of . Further use of the groups generated by
. Further use of the groups generated by
 and
and 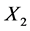 show that
show that 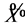 is equivalent to a scalar multiple of
is equivalent to a scalar multiple of  for some
for some .
.
Case 3. If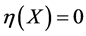 , there are two subcases. If not all of the coefficients
, there are two subcases. If not all of the coefficients 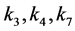 vanish, then we can choose
vanish, then we can choose 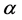 and
and 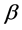 in (5) so that
in (5) so that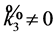 , but
, but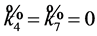 , so
, so  is equivalent to a multiple of
is equivalent to a multiple of
 . Suppose
. Suppose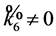 . Then we can make the coefficients of
. Then we can make the coefficients of 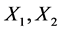
and  zero using the groups generated by
zero using the groups generated by  and
and , while the group generated by
, while the group generated by 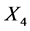 independently scales the coefficients of
independently scales the coefficients of 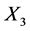 and
and . Thus such a
. Thus such a 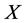 is equivalent to a multiple of either
is equivalent to a multiple of either
 for some
for some 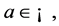
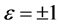 . If
. If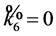 , so
, so  is equivalent to a multiple of
is equivalent to a multiple of
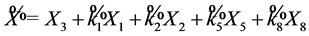 , suppose
, suppose . Then we can make the coefficients of
. Then we can make the coefficients of 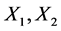 and
and 
zero using the groups generated by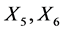 , and
, and , while the group generated by
, while the group generated by 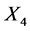 independently scales the coefficients of
independently scales the coefficients of 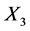 and
and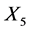 . Thus such a
. Thus such a  is equivalent to a multiple of either
is equivalent to a multiple of either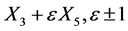 . If
. If
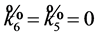 , then the group generated by
, then the group generated by 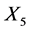 and
and 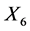 can be reduce
can be reduce 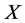 to a vector of the form
to a vector of the form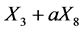 for some
for some .
.
The last remaining case occurs when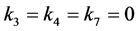 , for which our earlier simplifications were unnecessary. If
, for which our earlier simplifications were unnecessary. If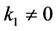 , then using groups generated by
, then using groups generated by 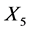 and
and  we can arrange
we can arrange 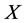 to become a multiple of
to become a multiple of
 for some
for some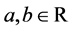 . If
. If , but
, but ,
,  , then we can make the coefficients of
, then we can make the coefficients of  and
and  zero using the groups generated by
zero using the groups generated by 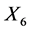 and
and , while
, while  is equivalent to a multiple of
is equivalent to a multiple of  for some
for some . If
. If , but
, but , we can first act by
, we can first act by
 and get a nonzero coefficients in front of
and get a nonzero coefficients in front of  which is reduced to the previous case. If
which is reduced to the previous case. If
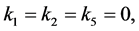 but
but ,
, 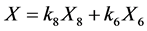 then we can arrange
then we can arrange 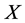 to become multiple of
to become multiple of 
for some . The only remaining vectors are the multiple of
. The only remaining vectors are the multiple of .
.
In summary, an optimal system of one-dimensional subalgebras of 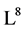 with base (4) is provided by generators
with base (4) is provided by generators
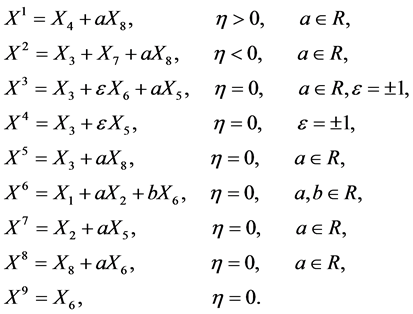 (6)
(6)
4. First Optimal Reductions of 2D-CNLS (1) with (6)
In this section, we give a classification of symmetry reductions of 2D-CNLS (1) by using optimal system (6).
Since the similarity, we will introduce the details of computation for  in (6) and directly give the computation results without showing the details of the procedure for the remaining cases in (6).
in (6) and directly give the computation results without showing the details of the procedure for the remaining cases in (6).
The differential invariants (and hence the similarity variables) for the generator 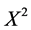 can be obtained by solving the characteristic system
can be obtained by solving the characteristic system
 (7)
(7)
The system yields the similarity variables as follows

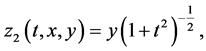

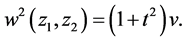
Hence we let
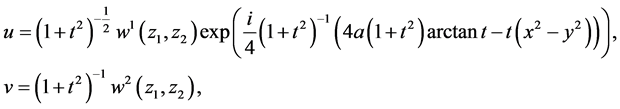 (8)
(8)
and substitute them into the equations (1), then the equations are reduced to
 (9)
(9)
Using the rest elements in (6), we can obtain the rest reductions of 2D-CNLS Equations (1) presented in following Table3 Here
5. Further Optimal Reductions of (1) through Reductions of the Equations in Table 3
In fact, the equations in Table 3 can be reduced further in the similar way which results in the second time reductions of 2D-CNLS (1). We take the second case in Table 3 as example to show the procedure of the second time reduction of the equation (1).
Using characteristic set algorithm given in [14] [15] , the symmetry algebra generators of the second equations (9) with similarity variables of case B in Table 3 is determined as follows
 (10)
(10)
Using the same procedure in last section, we can also find an one-dimensional optimal system of one-dimensional subalgebras of the Lie algebra spanned by (10). The optimal system consists of
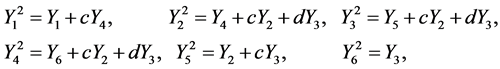 (11)
(11)
where ,
,  are arbitrary constants. We take
are arbitrary constants. We take 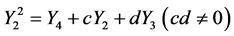 as example to show the further
as example to show the further

reduction procedure.
The characteristic system
 (12)
(12)
yields the corresponding similarity variables
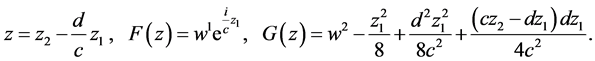
Hence we let
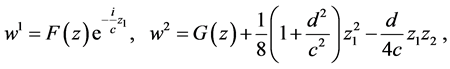 (13)
(13)
and substitute them into the underline equations, then the second equation in Table 3 is reduced to
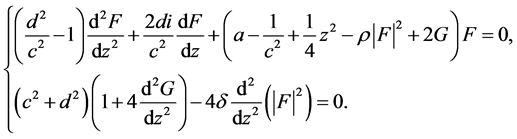 (14)
(14)
This is a result of twice reductions of (1) by 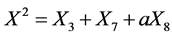 and
and  successively. In the same manner, we can obtain the other reductions of the equation with using the other elements in (11) which are listed in the following Table4 In fact, (13) and (14) are listed as second case in Table4
successively. In the same manner, we can obtain the other reductions of the equation with using the other elements in (11) which are listed in the following Table4 In fact, (13) and (14) are listed as second case in Table4
Solving the second equation in (14), we have

where 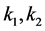 are arbitrary constants. Substituting this into the first equation of (14), we get a scale reduction of 2D-CNLS (1) as follows
are arbitrary constants. Substituting this into the first equation of (14), we get a scale reduction of 2D-CNLS (1) as follows
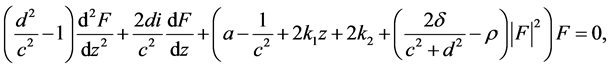
where

where 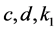 and
and  are arbitrary constants.
are arbitrary constants.
For 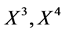 and
and , we also have optimal systems and the corresponding reductions which are given in
, we also have optimal systems and the corresponding reductions which are given in
Table 5, Table 6, Table 7 and Table 8 respectively.
6. Conclusion
In this paper, the infinite dimensional Lie algebra of 2D-NLS equations (1) is determined. The optimal system of a sub-algebra 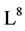 of the infinite dimensional Lie algebra is constructed using method given in [12] -[14] . As a result, the first reductions of the 2D-NLS equation (1) is presented by infinitesimal invariant method [14] [15] . The corresponding optimal systems of the Lie algebras admitted by the first reduced equations are also constructed. Consequently, the second time reductions classifications of the 2D-NLS equations (1) are obtained by these optimal systems. The twice reduction procedure shows that the 2D-NLS equation (1) can be reduced to a group of ordinary differential equations, which is helpful to explicitly solve the 2D-NLS equations (1).
of the infinite dimensional Lie algebra is constructed using method given in [12] -[14] . As a result, the first reductions of the 2D-NLS equation (1) is presented by infinitesimal invariant method [14] [15] . The corresponding optimal systems of the Lie algebras admitted by the first reduced equations are also constructed. Consequently, the second time reductions classifications of the 2D-NLS equations (1) are obtained by these optimal systems. The twice reduction procedure shows that the 2D-NLS equation (1) can be reduced to a group of ordinary differential equations, which is helpful to explicitly solve the 2D-NLS equations (1).
Table 5. The second reductions of 2D-CNLS (1) with X3.
where
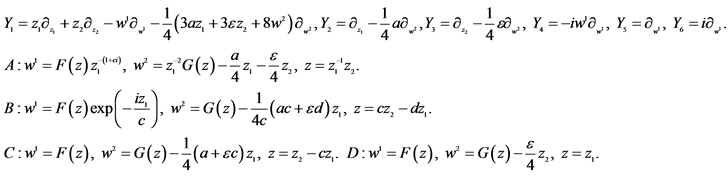
Table 6. The second reductions of 2D-CNLS (1) with X4.
where

Table 7. The second reductions of 2D-CNLS (1) with X5.
where

Table 8. The second reductions of 2D-CNLS (1) with X1, X6, X7, X8 and X9.
where

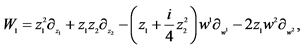
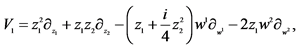
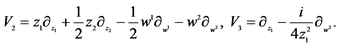
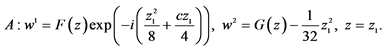




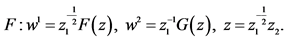

Acknowledgements
This research was supported by the Natural science foundation of China (NSF), under grand number 11071159.
References
- Benney, D.J. and Roskes, G.J. (1969) Wave Instabilities. Studies in Applied Mathematics, 48, 377.
- Davey, A. and Stewartson, K. (1974) On Three-Dimensional Packets of Surface Waves. Proceedings of the Royal Society of London. Series A, 338, 101-110. http://dx.doi.org/10.1098/rspa.1974.0076
- Djordjevic, V.D. and Redekopp, L.G. (1977) On Two-Dimensional Packets of Capillary-Gravity Waves. Journal of Fluid Mechanics, 79, 703-714.
- Freeman, C.N. and Davey, A. (1975) On the Soliton Solutions of the Davey-Stewartson Equation for Long Waves. Proceedings of the Royal Society of London. Series A, 344, 427-433. http://dx.doi.org/10.1098/rspa.1975.0110
- Ablowitz, M.J. and Haberman, R. (1975) Nonlinear Evolution Equations?? Two and Three Dimensions. Physical Review Letters, 35, 1185. http://dx.doi.org/10.1103/PhysRevLett.35.1185
- Satsuma, J. and Ablowitz, M.J. (1979) Two-Dimensional Lumps in Nonlinear Dispersive Systems. Journal of Mathematical Physics, 20, 1496. http://dx.doi.org/10.1063/1.524208
- Ablowitz, M J. and Segur, H. (1979) On the Evolution of Packets of Water Waves. Journal of Fluid Mechanics, 92, 691-715.
- Anker, D. and Freeman, N.C. (1978) On the Soliton Solutions of the Davey-Stewartson Equation for Long Waves. Proceedings of the Royal Society of London. Series A, 360, 529-540. http://dx.doi.org/10.1098/rspa.1978.0083
- Nakamura, A. (1982) Explode-Decay Mode Lump Solitons of a Two-Dimensional Nonlinear Schrodinger Equation. Physics Letters A, 88, 55-56. http://dx.doi.org/10.1016/0375-9601(82)90587-4
- Nakamura, A. (1982) Simple Multiple Explode-Decay Mode Solutions of a Two-Dimensional Nonlinear Schrodinger Equation. Journal of Mathematical Physics, 23, 417. http://dx.doi.org/10.1063/1.525361
- Tajiri, M.J. (1983) Similarity Reductions of the One and Two Dimensional Nonlinear Schrodinger Equations. Journal of the Physical Society of Japan, 52, 1908-1917. http://dx.doi.org/10.1143/JPSJ.52.1908
- Tajiri, M. and Hagiwar, M. (1983) Similarity Solutions of the Two-Dimensional Coupled Nonlinear Schrodinger Equation. Journal of the Physical Society of Japan, 52, 3727-3734. http://dx.doi.org/10.1143/JPSJ.52.3727
- Lbragimov, N.H. and Kovalev, V.F. (2009) Approximate and Renormgroup Symmetries. Higher Education Press, Beijing, 1-72.
- Bluman, G.W. and Kumei, S. (1991) Symmetries and Differential Equations. In: Applied Mathematical Sciences, Vol. 81, Springer-Verlag/World Publishing Corp, New York, 173-186.
- Ovsiannikov, L.V. (1982) Group Analysis of Differential Equations (Translation Edited by Ames, W.F.). Academic Press, New York, 183-209.
- Temuer, C.L. and Pang, J. (2010) An Algorithm for the Complete Symmetry Classification of Differential Equations Based on Wu’s Method. Journal of Engineering Mathematics, 66, 181-199. http://dx.doi.org/10.1007/s10665-009-9344-5
- Temuer, C. and Bai, Y.S. (2010) A New Algorithmic Theory for Determining and Classifying Classical and NonClassical Symmetries of Partial Differential Equations (in Chinese). Scientia Sinica Mathematica, 40, 331-348.
- Bluman, G.W. and Cole, J. D. (1974) Similarity Method for Differential Equations. Springer, Berlin.http://dx.doi.org/10.1007/978-1-4612-6394-4
- Olver, P.J. (1993) Applications of Lie Groups to Differential Equations. Spring-Verlag. New York/Berlin/Hong Kong.
- Bluman, G.W. and Anco, S.C. (2002) Symmetry and Integration Methods for Differential Equation. 2nd Edition, Springer-Verlag, New York.


