ABSTRACT

In many applications, a moving fluid carries a suspension of droplets of a second phase which may change in size due to evaporation or condensation. Examples include liquid fuel drops in engines and raindrops or ice-crystals in a thunderstorm. If the number of such particles is very large, and, if further, the flow is inhomogeneous, unsteady or turbulent, it may be practically impossible to explicitly compute all of the fluid and particle degrees of freedom in a numerical simulation of the system. Under such circumstances Lagrangian Particle Tracking (LPT) of a small subset of the particles is used to reduce the computational effort. The purpose of this paper is to compare the LPT with an alternate method that is based on an approximate solution of the conservation equation of particle density in phase space by the method of moments (MOM). Closure is achieved by invoking the assumption that the droplet size distribution is locally lognormal. The resulting coupled transport equations for the local mean and variance of the particle size distribution are then solved in conjunction with the usual equations for the fluid and associated scalar fields. The formalism is applied to the test case of a uniform distribution of droplets placed in a non homogeneous temperature field and stirred with a decaying Taylor vortex. As a benchmark, we perform a direct numerical simulation (DNS) of high resolution that keeps track of all the particles together with the fluid flow.

1. Introduction

In many multiphase flow problems, the condensed phase (liquid or solid) exists in the form of a cloud of droplets of heterogeneous size in an ambient gas undergoing time dependent (often turbulent) motion. One example is the problem of the formation and growth of ice crystals in the “contrails” of aircraft [1]. Another example is the spray combustion engine where liquid hydrocarbon fuel is introduced into the combustion chamber as a fine jet. The jet subsequently breaks up into droplets which evaporate to form the fuel vapor that undergoes combustion [2, 3]. In atmospheric physics, raindrops are formed in an unsteady convecting airflow by condensing on ions or dust particles that serve as nucleii. The droplet size then grows at a rate that depends on the temperature and humidity in its local environment [4]. The dynamics of atmospheric aerosols are yet another example of problems in this class [5].

The need for modeling the condensed phase arises in both Large Eddy Simulation (LES) and Direct Numerical Simulation (DNS) of turbulent flows. In DNS, the size of a computational grid is typically within an order of magnitude of the Kolmogorov scale. However, if particle sizes and the average distance between particles is much smaller than this scale, then clearly some kind of a statistical description of the particles need to be adopted so as not to increase the computational effort by many orders of magnitude. In LES, the filter size, that determines the scale of the smallest resolved eddies, is intermediate between the integral scale and the Kolmogorov scale. Here, in addition to modeling the effective stress due to the subgrid scale motions, some statistical modeling is needed for the particle cloud if particle sizes and the distance between them are much smaller than the LES filter size.

Two types of approaches are typically considered for the description of the dispersed multiphase flows mentioned above. The first and most frequently used approach is “Lagrangian Particle Tracking” or LPT as described originally by Dukowicz [6] in the context of liquid sprays. Here the Navier-Stokes equations describing the fluid are solved in the Eulerian framework, but particle properties (such as drop radius) are computed in the Lagrangian frame attached to the particle. The size of the problem is reduced by following a much smaller number () of representative particles. Each such “computational” particle then represents “real” particles where

is the actual number of particles present. Quantities such as the total mass of vapor produced in a grid cell is calculated by multiplying the computed quantity by the scale factor. The LPT method has several limitations. For example, it is possible that the flow is such that the representative particles rapidly cluster in a small region leaving only a few sample points in the remainder of the flow. Further, an “average” particle may not be representative of the average of all the individual particles. For example, since smaller particles evaporate much faster than larger particles, the rate at which the radius of an average particle shrinks differs significantly from the rate at which the average radius in the particle cloud decreases. This point is discussed further later in the text.

The approach adopted in this paper is the method of moments or MOM applied to the conservation equation for the particle distribution function—usually referred to as the “General Dynamic Equation” or GDE in the aerosol literature. It has been used, for example, in studies of nucleation and growth of crystals in chemical engineering [7], and vapor condensation and growth in gases [8]. The main difficulty with the moment method is the classic “closure problem”; the equations for any finite set of moments generally contain moments from outside this class. There are broadly two approaches to dealing with this problem. As pointed out by Hulburt and Katz [7], for spherical particles whose rate of growth can be written in separable form, the moment equations are closed if the rate of growth can be written as a linear function of radius. This is however not the case for other (nonlinear) laws of particle growth. Problems in which a linear representation of the particle growth equation is acceptable are limited, but, when such a representation is justified the moment method works very well [8, 9]. This has motivated a generalization to the Quadrature Method Of Moments (QMOM or DQMOM). As the name suggests, it is based on approximating the integral on the right of the moment equation by a quadrature formula and has the virtue that it reduces to the exact closed moment equations if the particle growth rate is linear in the radius [10,11]. This formulation has been used in a wide range of applications including polydispersed gas-solid fluidized bed reactors [11] and aerosol dynamics [12]. The method is general, however it does require a matrix inversion at each grid point, the size of which depends on the accuracy with which it is desired to approximate the integral.

An alternate method of closing the moment hierarchy is to assume some specific form for the size distribution function but leave the parameters of this distribution function (which of course can be related to its moments) undetermined. Hulburt and Katz [7] adapted this method to describe aerosol particles. He used the Gamma function form to represent the distribution function of a nonnegative physical variable. Pratsinis [13] and others after him in the aerosol community made use of the lognormal form. If the form of the distribution function is not known a priori then of course the method cannot be applied. The most direct method that does not require any such a priori knowledge or assumptions is the discretized population balance approach or the classes method which essentially amounts to a full integration of Equation (1) for the distribution function but using a very course grid in the “r” dimension describing particle radius [14]. Thus, the particles are sorted into a few “bins” according to size and coupled transport equations are written for the number of particles in each bin. The limitation of the method is that a relatively large number of classes are required to get reasonably accurate results and this drives up the computational cost. Another approach is to adopt a Lagrangian framework to account for particle advection and use a Monte-Carlo approach to arrive at a particle size distribution at each location. The difficulty with this method is that it suffers from “noise” or sampling error. Control of these errors require a relatively large number of particles, usually 10 or more per grid control volume making it computationally quite expensive [15].

In the next section we briefly outline the general formalism of the MOM approach following Hulburt and Katz [7]. In Section 2 we introduce a droplet evaporation law and the lognormal distribution. The numerical experiment involving the decaying Taylor vortex is described in Section 3. The present model as well as the LPT method are compared to the DNS. Finally, the advantages as well as the limitations of these two approaches are discussed in Section 4.

2. The Closure Model

It is assumed that the smallest characteristic length scale, at which the flow is being represented (this may be the Kolmogorov scale in DNS or the filter width in LES) is much larger than particle sizes or interparticle distances, so that a cube of side still contains enough particles that the state of the system may be described by the distribution function,. Here is the number of particles of radius between “” and “” that are contained in an elementary volume “” around location “” at time. If, further, the particles are inertialess, so that they are advected passively by the flow and they do not undergo coalescence or break up, an evolution equation for n_p may be written as

(1)

where is generally a function of r as well as other scalar and vector fields (such as density of water vapor or fuel mass fraction, temperature etc.).

In MOM, one assumes that the size distribution of particles at a given location may be written as, where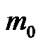, , are parameters, which without loss of generality, may be taken as the moments of the distribution. The functional form of “F” is presumed known. It then remains to determine evolution equations for the moments of the distribution, defined as. The first few moments are familiar, for example, 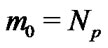, the total concentration of particles, where is the mean radius of the particles;, the variance of particle size distribution about the mean and, where is the liquid volume. In general, on taking the -th moment of both sides of (1) and using integration by parts, we have

(2)

The right-hand side may be evaluated if a differential equation for particle growth, and the assumed form of the probability density function (PDF) are given. If F is assumed to be a distribution with “n” parameters, then exactly “” moment equations must be retained so as to close the system and yet not “over determine” it.

We will take the evaporation law as

(3)

where and are constants, and is the temperature “at the location” of the particle. Here is the droplet temperature (assumed to be its boiling point) and: is the thermal conductivity of the gas, is the liquid density and is the latent heat of vaporization of the liquid. This assumes that the particle life time is much longer than a thermal diffusion time based on particle radius [16]. The cut-off at is introduced to avoid any difficulties associated with small denominators as the droplet evaporates, but it could also be thought of as the size of some inert condensation nucleus at the center of the droplet.

We will assume that the probability distribution is lognormal in the droplet radius r:

(4)

where the parameters and are easily seen to be related to, , and through the relations

(5)

The mean particle radius and the variance of the particle radius 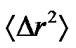are then related to and through the relations

(6)

If we get and; the variance normalized by the square of the mean.

Since in Equation (4) we have assumed a three parameter distribution, we need to retain just three moments in the infinite hierarchy of moment equations. Normally one would expect to write equations for the first three moments:, and. All other moments can then be computed using the distribution function (4). These computed values are approximate rather than exact and would not in general satisfy the moment Equation (2) exactly. This could lead to some difficulties. In particular, it can be shown that [17] the requirement that the volume of liquid can only decrease is not exactly satisfied leading to an unphysical exponential growth of liquid volume if droplet size becomes sufficiently small. Fortunately, the problem can be easily avoided by using the moment Equation (2) for the moments, and while regarding (and all other moments) as derived quantities. Further, using (5) those equations can be transformed into a form that uses, and as the dependent variables:

(7)

where the source terms and are given by

(8)

(9)

where

(10)

(11)

with and defined as follows:

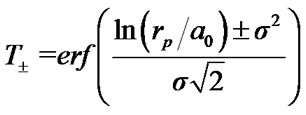(12)

3. Numerical Experiments

The model described in the last section (henceforth simply referred to as “the model”) will now be compared with a DNS containing a fairly large number of evaporating particles and an LPT simulation that is comparable in computational effort to the model. The flow configuration studied is a 2D decaying Taylor vortex. The following initial conditions are chosen for the velocity components:

(13)

(14)

and temperature distribution

(15)

(16)

We use isopropyl alcohol as the liquid phase, and we take (the boiling point of isopropyl alcohol) and, representative of the typical temperatures achieved in turbulent combustion. Table 1 shows the parameters used in the simulation. Figure 1 shows the initial streamlines and the temperature field. The Reynolds number is and we use 32 × 32 grid points for this two-dimensional calculation. To test the model’s predictions we performed a DNS by tracking 122,880 droplets which were initially randomly distributed over the computational domain. Approximately 120 droplets were obtained per grid cell providing statistically meaningful results. For DNS, the initial droplet sizes in each grid cell were sampled from the lognormal distribution (4) with a mean droplet radius of microns. Two cases with different initial variances () were investigated. Using the properties of isopropyl alcohol [18] the droplet life-time of a micron size drop can be estimated as,

(17)

This is shorter than an eddy turn over time (s) and much shorter than the viscous decay time of the eddies (s), so that for the duration of the computation, the vortices are essentially stationary in time.

3.1. Case 1 (Monodisperse Initial Condition)

For this case, at the initial time, the computational domain was seeded with droplets of a uniform size (). Figure 2 shows the time evolution of the droplet radius averaged over the entire domain, the total liquid mass in the droplets, and the fuel vapor mass fraction obtained from DNS and the model. All of these global averages are seen to be predicted very accurately by the model.

3.2. Case 2 (Polydisperse Initial Condition)

Keeping the flow conditions the same as in case 1, we introduce a small variance () in the initial droplet size distribution. For DNS, droplets in each grid cell were sampled from a lognormal distribution giving a scatter of around the mean droplet radius of

. Figure 3 shows the instantaneous distribution of fuel mass fraction obtained from DNS and the model at a later time. The time-evolution of the total liquid mass and fuel mass fraction in the computational domain (Figure 4) also show good agreement with the DNS. However, at large times, the mean droplet radius obtained using the model is lower than that of DNS (Figure 4). This, most likely, is an artifact of our sampling procedure: in a DNS, particles that have become too small are discarded so they are no longer counted in the calculation of the mean, resulting in the mean being higher than it should be. Figure 5 shows the comparison between the DNS and model for the instantaneous contours of mean droplet radius. It shows that the spatial variation in droplet radius is predicted well by the model.

Next we calculate the average droplet radius within each grid cell. Figure 6 shows the scatter plot for the mean droplet radius within each grid cell obtained from the DNS and the model. At, the mean droplet radii obtained from DNS and model are the same for all grid cells. The slight scatter is due to the fact that the droplets are generated by drawing a random sample from a specified

probability distribution and in a sample of finite size the sample mean differs slightly from the population mean by a random amount. With time, the mean droplet size decreases so that the cluster of points moves closer to the origin. However, they remain close to the diagonal line indicating that the DNS values and model predictions remain highly correlated. The cluster that falls somewhat above the diagonal line in the last panel corresponds to very large times and very small droplet radii. They are due to the afore mentioned artifact arising from discarding particles below a threshold size in the DNS.

Figure 7 shows the pdf of the variable

which should follow the unit normal distribution if is distributed lognormally. The data was obtained from the DNS and correspond to the individual points in Figure 6. From the DNS, we collect all

droplets in a grid cell, and use the data to determine and for that grid cell. Then the variable is calculated for each particle, the results binned and plotted. The same procedure is repeated for each grid cell. As shown in Figure 7, the droplet size distribution remains close to lognormal until most of the liquid has evaporated.

3.3. The Model vs. Lagrangian Parcels Tracking (LPT)

In simulations of practical gas-turbine combustor, the spray is represented by computational particles or “parcels” each representing a fixed number of droplets. Each parcel carries with it properties: velocity, mass, radiustemperature etc. equal to that of some “average” particle in the cloud that it represents [19,20]. Replacing a large clump of particles by a single “proxy” in this way reduces the computational cost to manageable levels. The accuracy of the algorithm as well as its computational cost is inversely correlated to the number of particles that a parcel represents. In order to compare the model with the LPT approach in regards to accuracy as well as computational cost, two separate simulations were run with the LPT method using the conditions corresponding to case 2 of the Taylor-vortex flow. We will call these cases (a) LPT1: 3072 parcels each representing 40 droplets and (b) LPT2: 128 parcels each representing 960 droplets. They both correspond to the same number (122,880) of droplets present in the DNS. These numbers are typical of a realistic spray simulation in complex combustors [2]. Figure 8 shows the instantaneous distributions of fuel vapor mass fraction obtained from DNS, the model, LPT1, and LPT2. It is seen that the accuracy in predicting the evolution of fuel mass fraction degrades considerably as one goes from 40 to 960 drops per parcel. Table 2 shows the comparison of CPU time per 100 iterations on a single processor of Origin 2000 for the four different approaches. It should be noted that the model and LPT1 have comparable computational cost, with the model actually producing somewhat better agreement with DNS at a cost that is slightly lower than the LPT1 simulation.

4. Conclusion

We introduce a model for handling two phase flows involving evaporating droplets which is essentially a moments method but with certain built in safeguards to render it stable against numerical instabilities and divergences arising due to small droplet diameters. The predictions of the model was compared to a DNS simulation involving evaporating droplets in a 2D Taylor vortex. For comparison, a competing LPT model with low and high number of representative particles was also run, the latter requiring roughly the same computational effort as the moments model.

REFERENCES