 Advances in Pure Mathematics, 2012, 2, 149-168 http://dx.doi.org/10.4236/apm.2012.23022 Published Online May 2012 (http://www.SciRP.org/journal/apm) Copyright © 2012 SciRes. APM Lattice of Finite Group Actions on Prism Manifolds John E. Kalliongis1, Ryo Ohashi2 1Department of Mathematics and Computer Science, Saint Louis University, St. Louis, USA 2Department of Mathematics, King’s College, Wilkes-Barre, USA Email: kalliongisje@slu.edu, ryoohashi@kings.edu Received October 12, 2011; revised December 11, 2011; accepted December 22, 2011 ABSTRACT The set of finite group actions (up to equivalence) which operate on a prism manifold M, preserve a Heegaard Klein bottle and have a fixed orbifold quotient type, form a partially ordered set. We describe the partial ordering of these actions by relating them to certain sets of ordered pairs of integers. There are seven possible orbifold quotient types, and for any fixed quotient type we show that the partially ordered set is isomorphic to a union of distributive lattices of a certain type. We give necessary and sufficent conditions, for these partially ordered sets to be isomorphic and to be a union of Boolean algebras. Keywords: Finite Group Action; Prism 3-Manifold; Equivalence of Actions; Orbifold; Partially Ordered Set; Distributive Lattice 1. Introduction This paper examines the partially ordered sets consisting of equivalence classes of finite group actions acting on prism manifolds and having a fixed orbifold quotient type. For a fixed quotient type, we show that the partially ordered set is a union of distributive lattices of a certain type. These lattices have the structure of factorization lattices. The results in this paper relate to those in [1], where those authors study a family of orientation revers- ing actions on lens spaces which is partially ordered in terms of a subset of the lattice of Gaussian integers or- dered by divisibility (see also [2]). Finite group actions on prism manifolds were also studied in [3]. Let M be a prism manifold and let G be a finite group. A G-action on M is a monomorphism :DiffGM where Diff is the group of self-diffeomorphisms of M. Two group actions :DiffGM and :G Diff are equivalent if there is a homeo-morphism :hM M such that 1 GhGh , and we let denote the equivalence class. If :DiffGM is an action, let :MM be the orbifold covering map. The set of equivalence classes of actions on prism manifolds forms a partially ordered set by defining if there is a covering : M such that . A prism manifold is defined as follows: Let 11 TSS be a torus where 1:1Sz z is viewed as the set of complex numbers of norm 1 and 0, 1I. The twisted I-bundle over a Klein bottle is the quotient space ,, ,,1WTIuvtuv t . Let D2 be a unit disk with 21 DS and let 12 VSD be a solid torus. Then the boundary of both V and W is a torus 11 SS . For relatively prime integers b and d, there exist integers a and b such that 1ad bc . The prism manifold , bd is obtained by identifying the boundary of V to the boundary of W by the homeomorphism :VW defined by ,, ab cd uvuv uv for 1 ,uvV S 1 S. The integers b and d determine , bd , up to ho- meomorphism. An embedded Klein bottle K in , bd is called a Heegaard Klein bottle if for any regular neighborhood NK of K, NK is a twisted I-bundle over K and the closure of , bdN K is a solid torus. Any G-action which leaves a Heegaard Klein bot- tle invariant is said to split. We describe in Section 2, the G-actions (up to equiva- lence) which can act on a prism manifold and the seven possible quotient orbifolds , i for 17i where and are some positive integers. For example, the orbifold 1, is an orbifold whose underlying space is a prism manifold with a simple closed curve as an exceptional set of type .. ,kgcd . The closure of the complement of the exceptional set is a twisted I-bundle over a Klein bottle. Section 3 gives necessary and sufficient conditions for an orbifold of type , i to be regularly covered by a prism manifold. Let , i be the partially ordered set of equiva- lence classes of G-actions with orbifold quotient  J. E. KALLIONGIS, R. OHASHI Copyright © 2012 SciRes. APM 150 , i . Define a set 1,, :..,1, divides,1 (mod2),andor2. bdgcd bdb dd b We show in Sections 4 and 6 that the set 1, is a distributive lattice which is isomorphic as a partially or- dered set to 1, , and this implies that 1, is also a distributive lattice. For 27i , we show that , i is isomorphic as a partially ordered set to a union of lattices of type 1, y. In addition, we give necessary and sufficient conditions for two lattices of type 1, y to be isomorphic. A G-action is primitive if it does not contain a non- trivial normal subgroup which acts freely. These actions determine minimal elements in the partially ordered sets. We determine the primitive actions for each possible orbifold quotient in Section 5. In Section 6 we compute the maximum length of a chain in the partially ordered sets , i . Further- more, if 0 b is the largest odd divisor of such that 0 .. ,1gcd b and 01 i kl i i bp is the prime decom- position, then we show that 1, is a Boolean al- gebra if and only if 1 i l for all 1ik. When 1,mn is a prism manifold, we consider in Section 7 a partially ordered set of non-cyclic subgroups ,mn of 11 π,mn. We show that ,mn is a lattice isomorphic to 1,mn where the partial order- ing on the groups is given by 21 GG if 2 G is a sub- group of 1 G. The meet 1212 ,GG GG and the join 1212 GGG G. Moreover we show that there exists a sublattice of ,mn which is a Boolean algebra, and a lattice homomorphism ,mn which re- stricts to the identity on . Section 8 is devoted to several examples which illus- trate some of the main results. 2. Actions on Prism Manifolds In this section we describe a set of G-actions on a prism manifold , bd which leave a Heegaard Klein bottle invariant and their quotient spaces , bd G. We obtain seven quotient types , i for 17i where and are some positive integers. It follows by [4] that any G-action which leaves a Heegaard Klein bottle invariant is equivalent to one of the actions in Quotient type [i] for some 17i, and ,, i Mbd G . By [4] these actions are completely determined by their restriction to a Heegaard Klein bottle K. We begin by describing G-actions on K and note that these actions extend to all of , bd . We will list the actions by their quotient type. Let Vk be the orbifold solid torus with exceptional set the core of type k and let BkV k be the Conway ball, where :Vk Vk is the involution defined by ,,uvuv . The Conway sphere Bk has 4 cone points, each of order 2. It is convenient to view the Klein bottle as the set of equivalence classes 1 :1 22,, 11 1,, 22. 22 Kru ruS uuuuu 1) Quotient type 1, . For 21mn, define actions 1:Diff m and 12 :Diff m by 2π 21 1 i n ru rue and π 21 1 1 1 i n ru ue r where 1 represents a generator of the group. The quotients 1 K and 1 K are both Klein bottles. These actions extend to the prism manifold , bd and we denote these extensions using the same letters to obtain 1:Diff, m bd and 12 :Diff, m bd . The orbifold quotient for these actions is denoted by 11 ,Vk W , where 1 W is a twisted I-bundle over the Klein bottle and :i Vk W is defined by ,, kk uvuvuv where and are inte- gers, and ,kgcd . It follows that the quotient 1 ,Mbd is the orbifold denoted by 121,bn d and the qoutient 1 ,Mbd is the orbifold denoted by 121,2bn d. 2) Quotient type 2, . For 2mn define ac- tions 2:Diff m and 22 :Diff m by π 21 i n ru rue , and 2 1 1, 0ru u r and π 21, 0 i n ru rue . The quotients 2 K and 2 K are both mirrored annuli. These actions extend to all of , bd and we obtain 22 :Diff, n bd and 22 2 :Diff, n bd . The orbifold quotient for these actions is denoted by 22 ,Vk W , where 2,,, ,1WTIuvtuvt is a twisted I-bundle over the mirrored annulus mA and ψ is defined as in Case 1. The orbifold quotient 22 ,2, bd nbd and 22 ,2,2 bdnb d . 3) Quotient type 3, . Define 32 21 :n Diff and 34 :Diff n by 3 1 1, 0ru u r , π 21 31, 0 i n ru rue , and  J. E. KALLIONGIS, R. OHASHI Copyright © 2012 SciRes. APM 151 π 2 3 1 1 i n ru ue r . The quotients 3 K and 3 K are mirrored Möbius bands. These actions extend to the prism manifold , bd and we obtain 3221 :n Diff , bd and 34 :Diff, n bd . The or- bofold quotient for these actions is 33 ,Vk W 3 VkW where 3,, ,,1WTIuvtvut is a twisted I-bundle over the mirrored Möbius band mM. The orbifold quotient 33 ,21,21 bdb ndbnd and 33 ,2,2 bdnb dnb d . 4) Quotient type 4, . For 21mn, define the action 421 :Dih Diff n by π 21 41, 0 i n ru rue and 4 1 0,1 ru u r . The quotient 4 K is the projective plane 22, 2P containing two cone points of order two. This action ex- tends to , bd and we obtain 421 :Dih n Diff , bd . The orbifold quotient is 4, 4 Bk W where 4,,1WIztzt is the twisted I-bundle over 22, 2P and is the homeo- morphism of induced by . The orbifold quotient 44 ,(21), bdb nd . 5) Quotient type 5, . Define the following ac- tions: 521 :Dih Diff n where π 21 51,0 i n ru rue and 50,1 ru ru ; 542 :Dih Diff n where π 21 5 1 1, 0 i n ru ue r and 50,1 ru ru ; 542 :Dih Diff n where 2π 42 51, 0 i n ru rue and 5 1 0,1 ru u r ; and 54 :Dih Diff n where π 2 51, 0 i n ru rue and 5 1 0,1 ru u r . The orbifold quotient for all these actions is the mirrored disk 22, 2. All these actions extend to Diff , bd . If 5,,1WIztrzt , where r is a reflection exchanging a pair of cone points, is the twisted I-bundle over 22, 2, then the orbifold quotient for these ex- tended actions is 55 ,Bk W . We obtain 55 ,21, bdb nd , 35 ,21,2 bdb nd , 55 ,42, bdb nd and 55 ,4, bd nbd . 6) Quotient type 6, . Define actions 66 ,: 2 Dih Diff n as follows: π 6 1 1, 0 i n ru ue r and 60,1 ru ru if n is even, and 2π 6 1 1, 0 i n ru ue r and 6 1 0,1 ru u r if n is odd. The quotients 5 K and 5 K are both a mirrored disk 22 containig a cone point of order two and two cone points of order two on the mirror. These actions extend to the prism manifold , bd and we obtain 66 2 ,:Dih n Diff , bd . The orbifold quotient for these actions is denoted by 66 ,Bk W where 6,,1WIztrzt the twisted I-bundle over the mirrored disk 22, and r is a reflection leaving two cone points fixed and exchanging the other two cone points. The orbifold quotients 5 ,Mbd and 6 ,Mbd are both 6,bnd bnd. 7) Quotient type 7, . Define 72 :Dih n Diff and 722 :Dih Diff n as fol- lows: π 71, 0 i n ru rue , 70,1 ru ru , and 7 1 1, 0,0ru u r , π 70,1,0 i n ru rue , and 70, 0,1ru ru . The quotients 7 K and 7 K are both a mirrored disk 20 containig four cone points of order two on the mirror. These actions extend to the prism manifold , bd and we obtain 72 :DihDiff , n bd and 722 :DihDiff , n bd . If 7,,1WIztrzt , where r is a reflection leaving each cone points fixed, then 7 W is a twisted I-bundle over the mirrored disk 20. The orbifold quotient for these extended actions is 6, 6 Bk W . We obtain 77 ,2, bd nbd and 77 ,2,2 bdnb d . 3. Prism Manifold Covers of Orbifolds In this section we give necessary and sufficient condi-  J. E. KALLIONGIS, R. OHASHI Copyright © 2012 SciRes. APM 152 tions for when the orbifold , i , 17i, is cov- ered by a prism manifold. The proofs rely on Section 2. Proposition 1. For the orbifold 1, , there exists a prism manifold cover if and only if either is odd or 0 (mod 4). Proof. Suppose is odd. Then there exists a -ac- tion on 1,M such that 1 1, 1,,MM . If is even, write 0 2l where 0 is odd. If is odd, then there exists a 0 -action on 2, l M such that 01 2, 2,, ll MM . Suppose now that and are both even where 0 (mod 4). Write 0 2 and 0 2m where 0 and 0 are both odd. Then there exists a 0 2 -action on 0 2, m M such that 0 002100 2,2,2 ,2 mm m MM . For the converse, suppose that and are both even and there is a covering ,, i Mbd . Then ei- ther 21bn and d , or 21bn and 2d . Since is even, it follows that 2 divides b. In the first case, 2 would also divide d, contradicting the fact that b and d are relatively prime. If 0 (mod 4), then again 2 divides d giving a contradiction. Proposition 2. For the orbifold 2, , there exists a prism manifold cover if and only if 0 (mod 2). Proof. Suppose that 0 (mod 2). Write 0 2 . Then there exists a 0 2 -action on 1,M such that 0 22 1, 1,,MM . For the converse, suppose that 2 ,,Mbd . Then either 2nb and d , or 2nb and 2d . Proposition 3. For the orbifold 3, , there exists a prism manifold cover if and only if (mod 2). Proof. Suppose that (mod 2) and let 2 d . Suppose that 0 (mod 4), and thus there exists an integer n such that 4n . There exists a 4n - action on 1, d such that 43 3 1,1,2, 2 ,. n dMd ndnd If 0 (mod 4), then write 21 2n for some n. There exists a 22 1n -action on 1, d such that 3 22 1 3 1,1,21,21 ,. n dMdn dn d For the converse, suppose that 3 ,,Mbd . Then either 21bnd and 21bnd , or 2nb d and 2nb d for some n. Subtracting the two equations in both cases, we obtain 2d . Propo sitio n 4. For the orbifold 4, , there exists a prism manifold cover if and only if either is odd or is odd. Proof. Since 1 ,Mbd always double covers 4 ,Mbd , using a proof similar to that in Proposition 1 shows that there is a prism manifold covering of 4, if and only if or is odd by [4]. Proposition 5. A prism manifold covering for the orbi- fold 5, always exists. Proof. Suppose is an odd number. Then 1,M admits a Dih -action whose quotient is 5, . If β is even, we write 0 2m where m ≥ 1, 0 2n where 0n, and 0 and 0 are both odd numbers. If n = 0 or 1n , then 2, m M and 0 2, m M admit 0 Dih and 0 2 Dih -actions respectively, whose quotient space is 5, . If n and m are both greater than 1, or if 1m and 2n, then 1,M admits a 10 42 Dih m or a 0 2 Dih -action respectively, whose quotient space is 5, . Proposition 6. For the orbifold 6, , there exists a prism manifold cover if and only if (mod 2). Proof. Since 3 ,Mbd double covers 6 ,Mbd and 3 ,Mbd double covers 6 ,Mbd , the re- sult follows by Proposition 3. Proposition 7. For the orbifold 7, , there exists a prism manifold cover if and only if 0 (mod 2). Proof. Since 2 ,Mbd double covers 7 ,Mbd and 2 ,Mbd double covers 7 ,Mbd , the re- sult follows by Proposition 2. 4. Poset of Actions on Prism Manifolds Recall that two group actions :DiffGM and :DiffGM are equivalent if there is a homeo- morphism :hM M such that 1 :Gh Gh . If :DiffGM is an action, let :MM be the orbifold covering map. Let be the set of equivalence classes of actions on prisim manifolds which leave a Heegaard Klein bottle invariant. Now is partially ordered by setting if there is a covering : M such that . Note that the covering : M is also a regular covering. For a pair of positive integers and let 1, denote the equivalence classes of those actions whose quotient type is 1, . Note that by Proposition 1 the set 1, is nonempty if and only if either is odd, or 0 (mod 4). Unless otherwise stated, we assume from now on that and are integers where either  J. E. KALLIONGIS, R. OHASHI Copyright © 2012 SciRes. APM 153 is odd or 0 (mod 4). Let 1,, :..,1, divides,1 (2)and,or2. bdZZgcd bd bmoddd b It follows that 1, is a partially ordered set under the ordering 22 11 ,,bdbd if 21 bb and 21 dd. Let 1, be the subset of 1, consisting of all ordered pairs 1 ,,bd where d . Note that 11 ,, if is odd. Moreover, if 0 2 (mod 2) and β is even, then 11 ,,2 . Proposition 8. Let 11 ,bd and 22 ,bd be elements of the poset 1, . There exists elements ,bd and ,bd in 1, , such that 11 ,,bdbd and 22 ,,bdb d, and 11 ,,bd bd and ,bd 22 ,bd . Proof. Let 12 .. ,b gcdbb. Note that since i d or 2 for 1,2i, it follows that if 12 min ,ddd, then i dd. Thus b divides and d is or 2 . If b is even, then it follows that 2 divides both 1 bb and 2 bb, contradicting 12 .. ,bgcdbb. Thus b is odd showing 1 ,,bd . Moeover 11 ,,bdb d and 22 ,,bdb d. Let 12 .. ,blcmbb and d 12 max ,dd. It follows that b is odd, and hence 1 ,,bd . Furthermore 11 ,,bd bd and 22 ,,bdb d . Corollary 9. 1, is a lattice where for 11 ,bd and 22 ,bd in 1, the join 112 21212 ,,..,,min,bdb dgcdbbdd , and the meet 112 21212 ,,..,,max,bdb dlcmbbd d . Furthermore, 1, is a sublattice of 1, . Proposition 10. Let 11 ,bd and 22 ,bd be elements of 1, such that 22 11 ,,bdbd. Then there exists either a standard m -action 1 on 22 , bd , or a standard 2m -action 1 on 22 , bd , which we denote by , and a regular covering 22 2211 :, ,, bd MbdMbd . Proof. If 22 11 ,,bdbd, then 21 bb and 21 dd. Furthermore 1 d , or 1 2d and 2 d , or 2 2d . Now 1 2 bm b, 11 21bn , and 21 21bn for some integers m, n1 and n2. Since 1122 21 21bnb n , it follows that 21 21 21nmn , and therefore m must be odd. Since 21 dd , the only possibilities are 12 dd or 21 2dd. If 12 dd , then there exists a m -action 1 on 22 , bd such that 2222 111 ,, , bd MbdMbd . If 21 2dd , then there exists a 2m -action 1 on 22 , bd such that 2222 111 ,,, bd MbdMbd . Proposition 11. Let ,bd be an element of 1, . Then there exists either a standard 21n -action 1 on , bd , or a standard 22 1n -action 1 on , bd which we denote by , and a regular covering 1 :, ,,Mbd Mbd . Proof. Write 21n b . If d , then there is a 21n -action 1 such that 11 ,, ,Mbd Mbd . If 2d , then there is a 22 1n -action 1 on , bd such that 11 ,, ,Mbd Mbd . Theorem 12. For each pair of positive integers and , the poset 1, is isomorphic to the poset 1, . Proof. Define a function 11 :, ,f as follows: let 1 ,,bd . There exists either a stan- dard b -action if d , or a standard 2b -action if 2d on , bd , which we denote by , such that 1 ,, ,Mbd Mbd . Define 1 ,,fbd . Suppose 1112 22 ,, bd fbd . Since 1 and 2 are equivalent, there exists a homeomorphism 1122 :, ,hMbdMbd such that 1 12 Gh Gh . Since 11 , bd and 22 , bd are homeomorphic, it follows that 12 bb and 12 dd , showing f is one-to-one. Let 1, . Then there exist a prism manifold , bd such that 1 :, ,,Mbd Mbd . We may assume that b and d are both positive. By [4], η is equivalent to one of the standard actions 1 or 1 , and 1 ,21, bdb nd or 121,2bn d respectively, for some positive integer n. Therefore 1 b (mod 2) and d or 2d . If is either 1 or 1 , then ,fbd , showing f is onto. Suppose now that 22 11 ,,bdbd. Let 111 ,fbd and 22 2 ,fbd where 1 and 2 are the standard  J. E. KALLIONGIS, R. OHASHI Copyright © 2012 SciRes. APM 154 11 b and 22 b -actions respectively on 11 , bd and 22 , bd and 1 i or 2. We have the coverings 1111111 :, ,,MbdMbd and 11111 11 :, ,,Mbd Mbd . By Proposition 10 there is a standard 12 bb -action on 22 , bd where 1 or 2, and a regular covering covering 22 2211 :, ,, bd MbdMbd . Since these are standard actions and 2 12 1 b bb b it fol- lows that 21 . This shows that 21 . Corollary 13. 1, is a lattice. We will now consider maximal and minimal elements in 1, . Write 0 2n where 0 is odd. Then the maximal element in 1, is 2, n if is odd, and 2,2 n if is even. Note that if ,bd 1, , then 2n divides b and 2n b is odd. In de- scribing the minimal elements let 0 b be the largest odd divisor of 0 such that 0 .. ,1gcdb . If is odd or if 0n, then the minimal element in 1, is 0 2, nb , otherwise the minimal element is 0 2,2 nb . We say an element 11 ,bd is directly below 22 ,bd or that 22 ,bd is directly above 11 ,bd if whenever 112 2 ,,,bdbdb d, then either 11 ,,bd bd or 22 ,,bdb d. Theorem 14. Let 0 011 2, mb and 0 022 2, nc be the minimal elements in 1 11 , and 1 22 , respectively where 1 i or 2, and let 01 i km i i bp and 01 i sn i i cq be the prime decompositions. Sup- pose one of the following holds: 1) 1 and 2 are both odd. 2) 1 and 2 are both even and 00 0mn. 3) 1 and 2 are both even and 00 0mn. 4) 1 even with 00m and 2 odd. Then 1 11 , is isomorphic to 1 22 , if and only if ks and after reordering ii mn for 1, ,ik. If 1 is odd and 2 is even with 00n, then 1 11 , is isomorphic to 1 22 , if and only if 1 ks, after reordering ii mn for 1, 2,,1ik, and 1 k m. Proof. We will first assume that 1 and 2 are both odd. Suppose 11 112 2 :, ,f is an iso- morphism. Now 0 1 2, m and 0 2 2, n are the maxi- mal elements of 1 11 , and 1 22 , respec- tively, and 00 12 2, 2, mn f . The elements directly below 0 1 2, m in 1 11 , are 0 11 2,,, mp 0 1 2, m k p and the elements directly below 0 2 2, n in 1 22 , are 00 12 2 2,,,2, nn s qq . Since f must take the elements directly below 0 1 2, m to the elements directly below 0 2 2, n , it follows that ks . The elements directly above 01 ,b in 1 11 , are listed as 00 12 0 11 112 1 12 1 1 2,,2 ,,, 2, ii ki mmm m mm ii ii mmm ki ik pppp pp Similarly the elements directly above 02 ,c are 00 12 0 11 122 2 12 1 2 2,,2 ,,, 2,. ii ki nnnn nn ii ii nn n ki ik qqq q qq By reordering we may assume 00 11 12 2,2, jj ii mn mmnn ji ji ij ij fppq q for 1jk . The number of elements in 1 11 , is 11 k i im , and this equals the number of elements in 1 22 , which is 11 k i in . Let 0 11 11 111 1 11 ,, ,: 2,,. ji j m mm ji ij b ppb Similarly let 0 11 22 222 1 22 ,, ,: 2,,. ji j n nn ji ij c qqc It follows that 11 112 2 ,, jj f . Thus the number of elements in 1 11 , j which is 1 ji ij mm is equal to 1 ji ij nn the num- ber of elements in 1 22 , j . Using the equations 1 11 kk ii ij i mn and 11 jiji ij ij mmnn , we obtain 11, 11 i jij j jij ij n mm nmn and this implies that j mn for 1jk. We now suppose that 0 01 2, mb and 0 02 2, nc are the minimal elements in 1 11 , and 1 22 , respectively, and 01 i km i i bp and 01 i km i i cq are the prime decompositions. If 1 111 ,,b , then  J. E. KALLIONGIS, R. OHASHI Copyright © 2012 SciRes. APM 155 0 1 2i k ms i i bp where 0ii m . Define 11 112 2 :, ,f by 0 12 1 ,2 , i k ns i i fb q . It is not hard to check that f is an isomorphism. The proof in cases (2) - (4) is similar. We now assume that 1 is odd and 2 is even with n0 = 0. Since the argument is similar to the previous case, we will sketch the proof. The elements directly below 0 1 2, m in 1 11 , are 00 11 1 2,,,2 , mm k pp and the elements directly below 2 1, 2 in 1 22 , are 122 2 ,2,,,2,1, s qq . It follows that k = s + 1. The elements in 1 11 , directly above 0 01 2, mb are 00 12 0 11 112 1 12 1 1 2,,2 ,,, 2,, ii ki mmm m mm ii ii mmm ki ik pppp pp and the elements directly above 02 ,c are 12 1 11 1222 12 1 12 1 ,, ,,, ,, ii ki nn nn ii ii nn ki ik qqq q qq 02 ,2c . By relabeling we may assume that 011 12 2, , jj ii mn mm n ji ji ij ij fppq q for 11jk and 01 102 2,,2 ki mm m ki ik fppc . Now 1 11 12 1 kk ii ii mn , and for 1jk we have 12 1 ji ji ij ij mm nn . Using these two equations we obtain j mn for 11jk. The number of elements greater than or equal to 01 1 2, ki mm m ki ik pp and 02 ,2c is 1 ki ik mm and 1 11 k i in respectively. Since these two numbers must be equal, it follows that 1 k m . For the converse suppose that 01 i km i i bp where 1 k m and 1 01 i km i i cq . If 1 ,b is any element in 1 11 , , then 0 1 2i k ms i i bp where 0ii m , and 0 k s or 1. Let 1 1 12 1 ,,2 ks i i fb q if 0 k s , and 1 1 2 =1 , ks i iq if 1 k s. It follows that f is an isomorphism. For a pair of positive integers and , let 2, denote the equivalence classes of those actions whose quotient type is 2, . Let 2,, :..,1, divides,0 (2),andor2. bdgcd bd bmoddd b It follows that 2, is a partially ordered set under the ordering 22 11 ,,bdbd if 21 bb , 1 2 1 b b (mod 2), and 21 dd. The proof of the following theorem is similar to that of Theorem 12. Theorem 15. For each pair of positive integers and , the poset 2, is isomorphic to the poset 2, . We will now consider the structure of the partially or- dered set 2, . Write 01 2mbb where 0 b and 1 b are both odd and 0 b is the largest odd divisor of which is relatively prime to . Theorem 16. For each pair of positive integers and , the poset 2, is a disjoint union of lat- tices given by 2 1 10 1 0 111 10 0 , 2, if0(2) ,if0(4) (2,2),if0 (2) 2 mmj j mmj j bmod bmod bb mod Proof. We first assume that is odd. Note that for 1jm , we have 2 0 2, , mj b . It suffices to show that if 0 2, , mj bbd , then 0 2, mj b ,bd and hence 0 2, mj b is a minimal element, and if 2 ,,bd , then 0 ,2, mj bd b for some unique j where 1jm . Suppose 0 2, mj b ,bd , and thus 0 2mj b divides b, divides d, and 0 2mj b b is odd. Now d divides , which implies d . Since b divides 01 2mbb and .. ,1gcdb , it fol- lows that b must divide 0 2mb. Write 2w bb where b is odd. Now 0 2 2 w mj b b being odd implies wmj and b0 divides b . Note that 2mj bb divides 0 2mb. Thus b divides 0 b showing that 0 bb , and there- fore 0 2mj bb . Let 2 ,,bd . Since is odd, it follows that d . As above we have that b divides 0 2mb. Furthermore, 0 2mb b must be even. We may write 2r bb where 01rm , b is odd, and b di- vides 0 b. Therefore 0 ,2, r bd b . We now assume that is even and we write 2n where is odd. There are two cases to consider: n ≥ 2 and n = 1. Suppose first that n ≥ 2. Now 0,b 2, . We will show that 0,b is the minimal element in 2, . Suppose that 2 ,,bd and 0,,bbd . In this case d . Also since 0 b b  J. E. KALLIONGIS, R. OHASHI Copyright © 2012 SciRes. APM 156 and 0 b are both odd, it follows that b is odd. Since .. ,1gcdb and b is odd, it follows that b divides 0 b. Thus 0 bb showing that 0,b is the minimal ele- ment. Now let 2 ,,bd . Recall that d or 2d . If d , then since b and d are relatively prime, b must be odd. Furthermore, b must divide 0 b, and thus 0 ,,bd b . If 2d , then 1 2 2 n d and d is even since n ≥ 2. Now b and 1 2n d are relatively prime, which implies that b is odd. Again we have that b must divide 0 b, so that 0 ,,bd b . This shows that 0,b is the minimal element and 21 0 ,,b . We now consider the case when n = 1. Note that 2 0 2,2, mj b for 1 ≤ j ≤ m – 1 and 2 0,,b . We need to show that these are the minimal elements in 2, , and if ,bd 2, then either 0 ,2,2 mj bd b for some unique j or 0 ,,bd b . The proof to this is similar to case 1. Remark 17. Note that by Theorem 7 each 1 10 2, mmj jb and 11 10 2,2 mmj jb is a dis- joint union of isomorphic lattices. For a pair of positive integers and with > and even, let 3, denote the equivalence classes of those actions whose quotient type is 3, . Let 3,,: , 2 . .,1,divides. 2 bd d gcdb db It follows that 3, is a partially ordered set under the ordering 21 ,,bdbd if 21 bb and 1 2 1 b b (mod 2). Theorem 18. For each pair of positive integers and with > and even, the poset 3, is isomorphic to the poset 3, . Proof. Let 3 ,,bd and let 2 mb . Ob- serve that bmd and bm d . There exists a standard 2m -action 2 :Diff, m bd such that 33 ,,,Mbdbmdbm d where 3 if m is odd and 3 if m is even. Define 33 :, ,f by 3 ,,fbd . Suppose that 21 ,,bd bd. Let 1 1 2m b and 2 2 2m b and let 1 12 1 :Diff, m bd and 2 22 2 :Diff, m bd be the standard actions. It follows that 1 21 2 b mm b , and therefore 1 2m is a sub- group of 2 2m . Furthermore, 1 2 21 11 b b , which implies that 21 and thus f is order preserving. The proof that f is one-to-one and onto is similar to that in Theorem 12. We will now consider the structure of the partially or- dered set 3, . Write 2 2 m where is odd. Let 0 b be the largest positive odd divisor of which is relatively prime to 2 d . Theorem 19. For each pair of positive integers and with > , even, and 2 d , the poset 3, is a disjoint union of isomorphic lat- tices given by 1 00 3 1 0 2,if 0(4) , ,if0(4) mmj jbd mod bd mod Proof. Suppose first that 0 (mod 4) (equiva- lently d is odd). Note that 0 2jb divides 2 for 0jm , and since d is odd we have 0 .. 2,1 j gcdbd . It follows that 3 0 2, , jbd and 0 2, jbd is a minimal element of 1 0 2, jbd. Let 3 ,,bd . Write 2k bb where b is odd. Since b divides 2 2 m , it follows that 0km and b divides . Furthermore, b and d are relatively prime. Since 0 b is the largest positive odd divisor of which is relatively prime to d, it follows that b divides 0 b. Hence 1 0 ,2, k bdb d for a unique k. Now sup- pose 1 0 ,2, k bdb d for some k. By assumption 2 d . Since b divides 0 2kb and 0 2kb divides 22 m , it follows that b divides 2 , and hence 3 ,,bd . The proof for 0 (mod 4) is similar. Corollary 20. 1 00 3 1 0 2,if 0(4) , ,if0(4) mmj jbd mod bd mod For each pair of positive integers and , let 4, denote the set of equivalence classes of actions  J. E. KALLIONGIS, R. OHASHI Copyright © 2012 SciRes. APM 157 on prisim manifolds whose quotient space is 4, . Theorem 21. 41 ,, Proof. If 4, , then is equivalent to 521 :DihDiff, n bd for some integers n, b, and d where 21bn and d . Since ,bd 1, , define a function 41 :, ,f by , bd . It follows easily that f is an order preserving surjection. For each pair of positive integers and , let 5, denote the set of equivalence classes of actions on prisim manifolds whose quotient space is 5, . We now consider the structure of the partially ordered set 5, . Write 01 2mbb where 1 b is odd and 0 b is the largest odd divisor of that is relatively prime to . Theorem 22. 5 1 00 1 0 11 0 1 0 , 2,if0(2)and1 ,if0(4)and1 2,2,if0(2)and 1 2 ,if1 mj j m bmodm bmodm bmodm bm Proof. Suppose that 0 (mod 2). Let 5, . We have a covering 5 ,,,Mbd Mbd for some positive integers b and d. Now is equivalent to either of the standard actions 5 , 5 or 5 . The action 5 is impossible since is odd. We will de- fine a function 51 00 :, 2, mj j fb as fol- lows: if is equivalent to 5 , then 01 212 m bn bb for some n and d . Since b and d are relatively prime and 0 b is the largest odd divisor of that is relatively prime to , it follows that b divides 0 2mb. Thus 1 0 ,2, m bd b and we let 1 0 ,2, m fbdb . If is equivalent to 5 , then 01 422 m bn bb , and this implies that b must divide 1 0 2mb . Thus ,bd 11 0 2, mb and we define 11 0 ,2, m fbdb . If is equivalent to 5 , then 01 42 m nbb b for some n. Write 0 2k nn where 0 n is odd. This implies that b divides 2 0 2mkb where 02km . This shows that 12 0 ,2, mk bd b and we define 12 0 ,2, mk fbdb . We now show that f is an order preserving bijection. Note that there do not exist integers n, n, b, and b , such that 21221bn bn , or 214bn nb , or 22 14bn nb , if either b divides b or b di- vides b with odd quotient. This implies that f is one-to- one. Furthermore if 21 , then 2 and 1 are both equivalent to either 5 , 5 or 5 . From this it can be shown that 21 ff . To show f is onto, suppose 1 0 ,2, j bd b for 0jm. Let 0 221 jbn b for some positive integer n. If mj , then 01 1 221 mbbbnb , and since 1 b is odd we may write 21bn . Hence there is an action 521 :DihDiff , n bd such that 55 ,,Mbd , and thus 5 f ,bd . Similarly, if 1jm or if 1jm , we ob- tain actions 5 and 5 -actions respectively. This shows that f is onto. If 0 (mod 4), then if m = 1 there exist only 5 - actions, and if m > 1 there exist only 5 -actions. For 0 2 (mod 2), if m = 1 there exist only 5 and 5 - actions, and if m > 1 there exist only 5 and 5 -actions. If is odd and is even, then there exist only 5 and 5 -actions. The proof in all these cases is similar to the above. For each pair of positive integers and with > and even, let 6, denote the set of equivalence classes of actions on prisim manifolds whose quotient space is 6, . Theorem 23. For each pair of positive integers and , the poset 6, is isomorphic to the poset 3, . Proof. Let 6,1 . Now is a Dih n - action on a prisim manifold , bd and is equivalent to 6 if n is even or 6 if n is odd. Furthermore, 6 ,, bdbn dbn d , and therefore bn d and bn d . It follows that 3 ,,bd . Define a function 6 :,f 3, by , bd . Let 3 ,,bd . Therefore 2 bn and 2 d for some n . This implies bnd and bn d . If n is even there exists an 6 -action, and if n is odd there exists an 6 -action. Therefore f is onto. Let 111 , bd and 222 , bd and suppose 12 ff . Then 112 2 ,,bd bd and hence 12 bb and 12 dd . We also have 11 1 bnd and 22 2 bn d so that 12 nn. Recall that 1 and 2 are equivalent to either an 6 or 6 -action. If 12 nn is even, then both of them are equivalent to an 6 -action, otherwise they are both equivalent to a 6 -  J. E. KALLIONGIS, R. OHASHI Copyright © 2012 SciRes. APM 158 action. Hence 1 and 2 are equivalent showing f is one-to-one. If 12 , then there is a covering map 22 11 :, , bd Mbd where 12 dd. Hence, 21 21nbb for some n which shows 21 bb is an odd number. Therefore, we conclude 1122 ,,bdb d showing f is order preserv- ing. For each pair of positive integers and , let 7, denote the set of equivalence classes of ac- tions on prisim manifolds whose quotient space is 7, . The proof of the following theorem is similar to that of Theorem 23. Theorem 24. For each pair of positive integers and , the poset 7, is isomorphic to the poset 2, . 5. Primitive Actions on Prism Manifolds Let :Diff ,GMbd be a G-action on a prism manifold , bd with orbifold covering map :, ,Mbd Mbd . We say that is primitive if G does not contain a non- trivial normal subgroup which acts freely on , bd . Therefore for any nontrivial normal subgroup H of G, if 0:Diff , H Mbd , then 0 ,Mbd is not a manifold. In this section we determine when an action is primitive. Theorem 25. Let :Diff, m bd be a m - action on the prism manifold , bd . 1) If is equivalent to 1 , then is primitive if and only if for every prime divisor p of m, 0d (mod p). 2) If is equivalent to 1 , then is primitive if and only if b is even and for every odd prime divisor p of m, 0d (mod p). 3) If is equivalent to 2 or 3 , then is primi- tive if and only if either 2n m, or if p is any odd prime divisor of m, then 0d (mod p). 4) If is equivalent to 3 , then is primitive if and only if either 2m, or if p is any odd prime divisor of m, then 0d (mod p). Proof. We may suppose 1 . Then 21mn and if l is a subgroup of m and 0: ll Diff , bd , then 10 ,,,Mbdbld Mbd . Furthermore 1,bl d is a manifold if and only if .. ,1gcdbl d. Assume that is primitive and let p be a prime divisor of m. Consider the subgroup . Since .. ,1gcdb d and is primitive, it follows that ..,.., cdbp dgcdpdp. Thus p divides d. Now suppose that every prime divisor of m also divides d and let l be a subgroup of m . Let p be a prime divisor of l. Since l divides m, it follows that p divides m. Hence by assumption .. ,1gcdbl d, showing that is primitive. For part 2), suppose that 1 . Then 22 1mn and if l is a subgroup of m and 0: ll Diff , bd , then either 21ls and 10 ,,,Mbdbld Mbd , or 22 1ls and 10 ,21,2,Mbdb sdMbd . Furthermore 1,bl d is a manifold if and only if .. ,1gcdbl d ; and 121,2bs d is a manifold if and only if ..21,21gcdbsd . Assume first that is primitive. If p is an odd prime divisor of m, then the same argument used in the 1 case shows p divides d. Now 2 is a subgroup of m and we have a covering 12 ,,2,MbdbdMbd. Since is primitive, 1,2bd is not a manifold, and since .. ,1gcdb d it follows that 2 divides b. For the converse suppose that b is even, and if p is any odd prime divisor of m, then 0d (mod p). Let l be any sub- group of m . If l is odd, the proof that is primitive is identical to the 1 case. If l is even, then ..21,21gcdbsd , showing that is primitive. To prove part 3), suppose that is equivalent to 2 . Therefore 2ms and 22 :Diff, s bd is defined by π 21 i ru rue where ru is any point in the Heegaard Klein bottle K and 1 denotes a generator of 2 . If l is any subgroup of 2 and 2:Diff, ll bd , then 2π 1 i l ru rue where 1 denotes a generator of l . We now suppose that 2 is primitive and p be an odd prime divisor of 2ms . Letting lp, we obtain a covering 1 ,, , bdMbdbpd . Since 2 is primitive .. , 1gcdbp d , and since ..,.., cdbp dgcdpd, it follows that p divides d. Suppose 2n m . Then 2t l and 2ππ 1 22 1 ii tt ru ruerue . Now K is a mir- rored annulus, showing that ,Mbd is not a mani- fold, and thus 2 is primitive. Suppose now that 2n m , and if p is an odd prime divisor of m, then 0d (mod p). Assume there is a covering 1 ,, , bdMbdbld (Note that the quo- tient space cannot be 1,2bl d by definition of 2  J. E. KALLIONGIS, R. OHASHI Copyright © 2012 SciRes. APM 159 and 1 ). It follows that l is odd. Let p be any odd prime divisor of l. It follows that p divides m, and hence by assumption p divides d. Thus .. ,1gcdbl d, showing 2 is primitive. We now suppose that 3 . In this case 4ms and 34 :Diff, s bd where π 2 3 1 1 i ru ue r . If l is a subgroup of m , let 3:Diff, ll bd . Assume first that is primitive. Suppose p is an odd prime divisor of m and consider the primitive subgroup of m . Here lp , and since m p is even we have 2π 1 i p ru rue . Since is a primitive 1 -action on , bd , it fol- lows by the above that 0d (mod p). Now suppose 2n m and let l be a subgroup of m . Then 2t l and π 1 2 1 i t ru rue . In this case is an 2 - action and ,Mbd is not a manifold. Now suppose that every odd prime divisor of m also divides d. Let l be a subgroup of m . If l is odd, then 4 l is even and 2π 1 i l ru rue which is an 1 - action. The result follows by the above that is primi- tive, and thus is primitive. Now suppose l is even. If m l is even then 2ππ 1 ii ll ru ruerue , which is an 2 -action; and if m l is odd then 2ππ 11 1 ii ll ru ueue rr , which is a 3 -action. In either case the quotient is not a manifold. Hence is primitive. We now prove part 4) and suppose 3 . Therefore 22 1mn and 322 1 :Diff, n bd where 2π 21 3 1 1 i n ru ue r . If 2m, then 3 K is a mirrored Möbius band and the action is primitive. So suppose that 2m. Assume first that 3 is primitive and let p be an odd divisor of m, and hence p divides 21n. Consider the subgroup and let 3:Diff, pp bd . Then 4π 1 i p ru rue , and we have a covering 1 ,, , bdMbdbpd . Again as above since 3 is primitive, p must divide d. We now suppose that for each odd prime divisor p of m, 0d (mod p). Let l be a subgroup of m . If l is odd we obtain a covering 1 ,, , l bdMbdbld, and as above if p is a prime divisor of l we obtain .. ,1gcdbl d. Thus the action is primitive. If l is even then 22 1ls , and if 3l then 2π 21 1 1 i s ru ue r . In this case 3 ,, l bd bld, which is not a manifold show- ing that the action is primitive. Proposition 26. Let 22 :Diff, m bd be an action on the prism manifold , bd where 2m. Then is primitive if and only if either 2n m , or if p is any odd prime divisor of m, then 0d (mod p). Proof. We may assume that 2 , and therefore 2 22 m . Suppose that 2 is primitive. This implies that 2 is primitive and the result follows from Theo- rem 25. Now suppose that either 2n m, or if p is an odd prime divisor of m, then 0d (mod p). Note that this implies by Theorem 25 that 2 is primitive. Let H be a subgroup of 22m and 2 . If 211HZ , then ,Mbd is not a manifold. So we may assume that 211HZ , and hence H is a subgroup of 2m . Since 2 is primitive, ,Mbd is not a manifold showing that 2 is primitive. Proposition 27. Let 22 :Diff, bd be an action on the prism manifold , bd . Then is primitive if is equivalent to either 5 , 6 or 7 . If is equivalent to 2 or 5 , then is primitive if and only if 0b (mod 2). Proof. If is either 5 , 6 , 7 , 2 or 5 , then any subgroup of 22 restricted to a Heegaard Klein bottle K is a product of the following homeomorphisms where ru K : πi ru rue , ru ru, and 1 ru u r . The only fixed-point free action on K is the homeomorphism π 1i ru ue r . By definition of 5 , 6 or 7 , they do not contain this homeomor- phism, and hence they are primitive. But the actions 2 and 5 do contain this 2 subgroup and we obtain a covering 21 ,, ,2. bdMbdbd Since 1,2bd is a manifold if and only if 2 does not divides b, the result follows. Proposition 28. Let :DihDiff , m bd be an action on the prism manifold , bd for m > 2. 1) If is equivalent to either 4 or 5 , then is primitive if and only if for every prime divisor p of m, 0b (mod p). 2) If is equivalent to 5 , then is primitive if and only if b is even and for every odd prime divisor p of  J. E. KALLIONGIS, R. OHASHI Copyright © 2012 SciRes. APM 160 m, 0d (mod p). 3) If is equivalent to either 5 , 5 , 6 or 7 , then is primitive if and only if either 2n m, or if p is an odd prime divisor of m, then 0d (mod p). 4) If is equivalent to 6 , then is primitive if and only if either 2m or, if for each odd prime divi- sor p of m, 0d (mod p). Proof. We may assume is either 4 or 5 , and thus 21mn and 1 |m . If is primitive, then 1 |m is primitive, and the result follows by Theo- rem 25. For the converse, suppose that H is a subgroup of 12 Dihmm . If 21H, then , bd H is not a manifold. So we may assume 21H, and thus H is a subgroup of m . Hence l H for some l with l dividing m. By Theorem 25, 1 is primitive, and so , bd H is not a manifold. Thus 4 and 5 are primitive. The proof for the other cases is similar to Theorem 25. Proposition 29. Let 22 :DihDiff, m bd be an action on the prism manifold , bd . 1) If 2m, then is primitive if and only if either 2n m, or if p is any odd prime divisor of m, then 0d (mod p). 2) If 1m, then is primitive if and only if 0b (mod 2). Proof. We may assume that 7 . Since 22 72 m , using Propositions 26 and 27, a proof similar to that used in Proposition 28 proves the result. 6. Lattice Structure In this section we compute the maximum length of a chain in the partially ordered sets , i . In addition, we give necessary and sufficient conditions for 1, to be a Boolean algebra. Theorem 30. Let 11 ,bd and 22 ,bd be elements of 1, , and so ii d , where i is 1 or 2 for 1, 2i. Suppose 22 11 ,,bdbd. Then 2 b divides 1 b and 21 . 1) If 21 , then there exists ,bd in 1, such that 22 11 ,,,bdbdbd. 2) If 12 , then 1 2 b b is prime if and only if there does not exist ,bd in 1, such that 22 ,bd 11 ,,bdb d. Proof. Since 11 ,bd and 22 ,bd are elements of 1, for 1, 2i, it follows that .. ,1 ii gcd b d , i b divides , 1 i b (mod 2), and ii d where 1 i or 2. By the definition of 22 11 ,,bd bd, we have 21 bb and 21 dd . Now 12 21 d d , which implies 21 . Suppose 21 . Thus 22 and 11 , hence 21 2dd . Now 1 12 ,,bd and 22 1211 ,>,>,bd bd bd showing (1). We now suppose that 12 , and thus 12 dd . Sup- pose there exists ,bd in 1, such that 22 11 ,,,bdbdbd. It follows that 12 ddd , 2 bb and 1 bb. Therefore 11 22 bb b bb b . Note that 1 2 b b is prime if and only if either ,bd equals 22 ,bd or 11 ,bd . Corollary 31. Let 1 and 2 be elements of 1, , such that 11 1:Diff, m bd and 22 222 :Diff, m bd where mi is odd and i is either 1 or 2. Suppose 21 . Then 2 b divides 1 b and 21 . 1) If 22 and 11 , then there exists 1, such that 21 . 2) If 12 and 1 2 b b is prime, there exists no 1, such that 21 . Recall that the maximal element in 1, is 2, n if is odd, and 2, 2 n if is even. To obtain the minimal element let 0 b be the largest odd divisor of such that 0 .. ,1gcdb . The minimal element is 0 2, nb if either is odd or if 0n , otherwise the minimal element is 0 2,2 nb . Theorem 32. For the partially ordered sets , i where 17i and 3,6i , let 12 12 2k n nn n k pp p and 12 12 2k m mm m k pp p be the prime decompositions. Let 0 b be the largest odd divisor of relatively prime to . Thus, 12 012 k l ll k bpp p where 0 j l if and only if ,0 jj min nm and j ln if and only if ,0 jj min nm . Then the following chart gives the length of a maximum chain in each , i . The maximum length of a chain Ordered set Conditions Max. length 1, , 2, , 7, 0 (mod 2) 11 k i il 1, , 2, , 7, 0 (mod 2) 12 k i il 4, none 11 k i il 5, 0 (mod 2) and n = 0 or n ≥ 1 11 k i il 5, 0 (mod 2) and n = 0 12 k i il  J. E. KALLIONGIS, R. OHASHI Copyright © 2012 SciRes. APM 161 Proof. We will consider first 1, . Since 1, is isomorphic to 1, we will prove the result for 1, . Suppose that β and are both even, and thus 0,2b and 2,2 n are the minimal and maximal elements of 1, respectively. We may construct a chain in 1, 12 00101 1 01 ,2< ,2<,2< <,2< <2,2<2,2 lnn k bbpbp bp p such that dividing any two consecutive first coordinates yields a single prime in the prime decomposition of 0 b. Now the length of this chain is 11 k i il . Since any maximal chain must contain both the minimal and maximal elements, it follows by the above theorem that this is a maximal chain. The other cases for 1, are similar. For the case 2, note that 2, is iso- morphic to 2, , which by Theorem 16 is equal to 1 10 2, mmj jb if 0 (mod 2); 1 0,b if 0 (mod 4); or 11 1 10 0 2,2 , mmj jbb if 0 2 (mod 2). By Remark 17 each 1 10 2, mmj jb and 11 10 2,2 mmj jb is a disjoint union of isomorphic lattices. The result now follows by applying the above 1, case. By Theorem 21, 41 ,, . If is odd then 11 ,, , and the result follows by the above. If is even, then a chain in 1, can be con- structed as the above where the second coordinate is re- placed by proving this case also. By Theorem 22, 5, is isomorphic to 1 00 2, mj jb if 0 (mod 2) and m ≥ 1; 1 0,b if 0 (mod 4) and m ≥ 1; 11 0 2,2 , mb if 0 2 (mod 2) and m ≥ 1; or 1 0,b if 0m . Using the above results, the first three cases give the maximum length of 11 k i il . When 0m , then there is no restriction on . Thus the maximum length is 11 k i il if is odd and 12 k i il if is even. For the remaining case, it follows by Theorem 24 that 72 ,, , which in turn is isomorphic to 2, . The result now follows by the above. Theorem 33. For a pair of positive integers and with > , even, let 2 2 m where is odd. Let 0 b be the largest odd divisor of rela- tively prime to 2 d and let 12 12 2k ss s k ppp and 12 12 2k t tt t k pp p be their prime decompositions. Thus, 12 012 k l ll k bpp p where 0 j l if and only if ,0 jj min st and j ls if and only if ,0 jj min st . For the partially ordered sets 3, and 6, the maximum length of a chain is 11 k i il . Proof. By Theorems 18 and 23 it follows that 3, and 6, are both isomorphic to 3, , which is equal to 1 10 2, mmj jbd if 0 (mod 4) or 1, if 0 (mod 4). In both cases the maxi- mum length is 11 k i il . A lattice L is a distributive lattice if for any a, b, c in L, abcab ac . Proposition 34. 1, is a distributive lattice where for 11 ,bd and 22 ,bd in 1, the join 112 21212 ,,..,,min,bdb dgcdbbdd and the meet 112 21212 ,,..,,max,bdb dlcmbbd d . Proof. By Corollary 9, 1, is a lattice. A com- putation using the following equation max ,min,minmax ,,max ,lmnlm ln for any positive integers l, m and n, shows that 1, is a distributive lattice. Remark 35. If we represent the minimal element by 0 2, nb and the maximal element by 2, n where is either 1 or 2, then for any element 1 2, , nbd we have 0 2,2,2, nn n bd bbd and 2, 2,2, nn n bd bd . A lattice ,,B is said to be a Boolean algebra if the following hold: 1) B is a distributive lattice having a minimal element 0 and a maximal element 1. 2) For every aB , 0aa and 1aa . 3) For every aB there exists aB such that 1aa and 0aa . Proposition 36. For the partially ordered set 1, let 0 b be the largest odd divisor of such that 0 .. ,1gcdb and let 01 i kl i i bp be the prime decomposition. Then 1,,, is a Boolean algebra if and only if 1 i l for all 1ik. Proof. Suppose that 1 i l for all 1ik. By Remark 35 above and Proposition 34, it remains to show (3) of the definition. Let 1 11 2, , nbd . Now 10 22 nn bb  J. E. KALLIONGIS, R. OHASHI Copyright © 2012 SciRes. APM 162 and so let 0 2 1 b bb . Observe that 12 .. ,1gcd bb and 1212 0 .. ,lcmbbbbb. If either 0n and is even, or if is odd, then all the elements in 1, have the same second coordinate—either 2 in the first case or in the second case. In this case 11 2101 2,2,2 , nnn bd bdbd and 11 211 2,2,2, nnn bdb dd. The remaining case is 0n and even. If 1 d then let 22d , and if 12d we let 2 d . It follows that 112 2 2, 2, nn bdb d gives the minimal element and 112 2 2, 2, nn bd bd gives the maximal element. We now suppose that 1,,, is a Boolean algebra. Suppose there exists an >1 j l. The minimal element in 1, is 0 2, nb where is either 1 or 2. Now 1 0 2, n j bp is an element of 1, and 1 00 2,>2, nn j bp b . There exists a com- plement 2, nbd such that 1 00 2,2,2, nn n j bd bpb , and so 1 00 .. , j lcmbpbb . It follows that pj divides b. We also have 1 0 2, 2 nn bd bp equal to the maximal element 2, n , and so 1 0 ..2 ,22 nn n j gcdbb p . But since >1 j l, it follows that pj divides 1 0 bp , giving a contradiction. Proposition 37. Let 00 ,Ibd be an ideal of a lattice 1, such that 00 ,bd is directly below 2, nd which denotes the maximum element in the lattice. If 112 2 ,,bdb dI , then 11 ,bd I or 22 ,bd I and I is a maximal ideal. Proof. Let 112 20 0 ,, ,bdb dIb d . Suppose both , ii bd I for 1, 2i. Since there is no element between 00 ,bd and 2, nd, we have 00 ,,2, n ii bdb dd , where 0 ,2 n i g.c.d bb for 1, 2i. This says that i b and 0 b do not have a com- mon odd prime divisor for 1, 2i. On the other hand, 112 20 0 ,, ,bd bdbd so that 012 .. ,blcmbb . Since 0 b and i b do not have any common odd prime divisors, this forces 02n b . As 00 0 ,2, n bd d is not the maximum element, 02dd . This result is possible only when the second coordinate is allowed to have an even number, otherwise it would be contradiction. Note that the second coordinate is an even number so that we must have 0n, and hence 00 ,1,2bdd. In addition, both 1 b and 2 b must be odd numbers. Now, 112 20 0 ,, ,bdb dbd implies 02dd should divide 12 max ,dd. It follows that at least one of i d must be equal to 2d. We may assume 12dd and thus 111 ,,2bdbd. Since 1 b is an odd number and 01b , this shows 1100 ,,bd bd telling us 11 ,bdI , which is a contradiction. Remark 38. The converse of Proposition 37 is false. For example, consider 145,11. 9,11 is a prime ideal but not maximal. Corollary 39. Let 00 ,Ibd be an ideal of a lattice 1, such that 00 ,bd is directly below 2, nd which denotes the maximum element in the lattice. Let 0, 1L be a lattice where the partial ordering on L is defined by 01 . Then the following are true and equivalent. 1) I is a prime ideal. 2) 1, is a prime filter. 3) There is a homomorphism 1 :,DI with 0 I I . Proof. Condition (1) follows by Proposition 37, and conditions (2) and (3) follow by lattice theory (see for example [5]). Proposition 40. Let 00 ,Ibd be an ideal of a lattice 1, and 2, nd denotes the maximum ele- ment in the lattice. Suppose that if 112 2 ,,bdbd I, then 11 ,bd I or 22 ,bd I. If 1, is a Boo- lean algebra, then I is maximal and 00 ,bd is directly below 2, nd. Proof. Since 1, is a Boolean algebra, I is maximal. If 00 ,,<2, n bd bdd , then 00 ,,bd bd . This shows 00 ,,bd bd . 7. Group Lattice Structure Let m and n be relatively prime integers with >1n. De- fine the group π,mn to be 112 π,,, 1 mn m nxyyxyxyx . Let V and W denote a solid torus and a twisted I-bundle over the Klein bottle K respectively. Recall that the prism manifold , mn VW , where V is identified to W by a homeomorphism :VW defined by ,, mtn uvuv uv , where s and t are integers satisfying 1sn tm . The fundamental group of , mn is π,mn. Theorem 41. Let H be a normal subgroup of π,mn. Then, either H is cyclic or H is isomorphic to π,bd for some relatively prime integers b and d satisfying the following conditions: b divides m, 1 m b (mod 2), d = n and π,mb mn H, or 2d = n and 2 π,mb mn H. Furthermore, there exists a realizable isomorphism of π,mn such that if dn then , m b xy ,  J. E. KALLIONGIS, R. OHASHI Copyright © 2012 SciRes. APM 163 and if 2dn then 2, m b xy . Proof. Let H be a normal subgroup of π,mn. Let :, Mmn be the regular covering correspond- ing to H. Choose a component W of 1W and let 0: WWW . Since W is a twisted I-bundle over a Klein bottle K and 0:WW is a covering space, it follows that W is either TI where T is a torus or a twisted I-bundle over a Klein bottle. Note that each component of 1V is a solid torus. If W is TI , then there are two components of 1V whose boundaries are being identified with TI, and thus M is a lens space. In this case 1 π H is cyclic. If W is a twisted I-bundle over the Klein bottle, then there is only one component of 1V whose boundary is being identified with W, and hence M is a prism manifold. In this case , Mbd for some relatively prime integers b and d. Furthermore there is a group ac- tion G on , bd such that ,, bdGM mn. Now 1 is a G-invariant Klein bottle. Hence by [4], the G-action is equivalent, via a homeomorphism h of , bd , to either a standard 21r -action with 21mrb and nd, or a standard 22 1r -action with 21mrb and 2nd. These standard actions arise from the coverings of , mn corresponding to the subgroups , m b y and 2, m b y respecttively. Now h projects to a homeomorphism of , mn real- izing . Theorem 42. Let 11 11 π,, m b bdx y and 22 22 π,, m b bdx y be subgroups of π,mn where 1 i or 2. Then 12 max , 112 2 π,π,π,, m b bdb dbdxy where 12 ,bgcdbb and 12 min ,ddd. The group generated by 11 π,bd and 22 π,bd is 12 min , π,, m b bd xy where 12 .. ,blcmbb and 12 max ,ddd . Proof. Let 12 ,bgcdbb. Note that we have bi mbm bib yy for 1, 2i. This shows that 12 max , π,, m b bd xy is a subgroup of 112 2 π,π,bdbd H. Since H contains π,bd, it follows that H is not cyclic. By Theorem 41, H is isomorphic to π,ln or π,2ln . Furthermore, b divides l and l divides i b, and since 12 ,bg.c.dbb, it follows that bl. If 1 d or 2 d is 2n, then since H is a subgroup of π, ii bd , it follows by the above Theorem 41 that π,2 ln. Since π,bd is a subgroup of H, we must have 2dn showing π,bd H . We now suppose 12 dd n , and thus dn and π, ln. It follows that π,bd H . Let J be the group generated by 11 π,bd and 22 π,bd. Now 12 min , x is clearly a generator of J and π,bd . Since bm mbib bi yy , we have J contained in π,bd . To show π,bd is contained in J, we use the easily verifiable equation 12 12 ..,.., mm cdlcm bbm bb , and by using 12 .. ,blcmbb we have 12 .. , mm m gcdbbb . Since there exist integers s and t such that 12 mmm st bb b , we obtain 12 st mm m bb b yy proving the result. Let ,mn be the collection of subgroups π,, m b n bxy of π,mn where 1 or 2. Theorem 43. ,mn is a lattice of subgroups, and there exists a lattice isomorphism 1 ,,mn mn which sends an element π,bd in ,mn to the element ,bd in 1,mn. Proof. If 11 π,bd and 22 π,bd are elements in ,mn, define 112 2 π,π,bdb d if 22 π,bd is a subgroup of 11 π,bd . For 11 π,bd and 22 π,bd in ,mn, define 112 21122 π,π,π,π,bdb dbdb d and 112 2 π,π,bdbd to be the group generated by 11 π,bd and 22 π,bd . By the above Theorem 42, ,mn is a lattice. Furthermore, the map which sends an element π,bd in ,mn to the element ,bd in 1,mn is a lattice isomorphism. Corollary 44. ,mn is a distributive lattice, which is a Boolean algebra if and only if the prime decomposi- tion of m is 1 2k j i ip . Proof. This follows by Propositions 34 and 36 and Theorem 43.  J. E. KALLIONGIS, R. OHASHI Copyright © 2012 SciRes. APM 164 For the following propositions write 0 k mpm where p is an odd prime relatively prime to 0 m. Proposition 45. Let π, ln pb and π,n pb be subgroups of π,mn where 1l. There exists a sur- jection :π,π, l l nn pb pb . Proof. Since π,, l m lpb n pbx y and π,, m pb n pbx y , define a function :π,π, l l nn pb pb by l x and l mm bpb lyy . Clearly l preserves the first relation in π, ln pb . To show that l preserves the second relation, it suffices to show that 1 21 l pmn yx . Write 121 l ps , and note that 121 2 22 22422 lss s mmm mmmm yy yyyyy , since 41 m y. Thus 1 22 1 l pmn mn yxyx , showing that l is a homomorphism. Since l takes generators to generators, it is also a surjection. Proposition 46. Let 21 21 21 π,π, ll nn pb pb be subgroups of π,mn where 12 1ll. There exist sur- jections :π,π, i i l li i ii nn pb pb for 1, 2i and a homomorphism 11 11 :π,π, nn pb pb , such that the following diagram commutes where and are inclusions: 2 2 2 π, ln pb 2 l 2 2 π,n pb 1 1 1 π, ln pb 1 1 π,n pb 1 1 π,n pb 1 l Proof. Let 21 2211 21 21 21 π,, ,π, ll mm lpbpbl nn pbxyxypb . Note that 2 b divides 1 b, 21 and 21 ll . By Proposition 45, there exist surjections :π,π, i i l li i ii nn pb pb defined by ii i l x , = liii i mm bpb lyy . Define a function 11 11 :π,π, nn pb pb by 11 x and 11 l mm pb pb yy where 12 lll. Let 1 0 c and 1 1 m pb yc , and note that the relations in this group are 11 101 0 ccc c and 11 2 10 1 n pb cc . Write 21 l ps and observe that 11 111 21 22 422 11 111 l pss bpbpbpbpb cc ccc , since 1 4 11 pb c . Therefore 111 111 22 2 1010 10 1 l nnn p pb pbpb cccc cc . Clearly preserves the other relation, showing that is a homomorphism. Since 2 2 l pb divides 1 1 l pb and 2 divides 1 , it fol- lows that the inclusion homomorphisms and are defined as follows: 2 21 1 xx and 11 22 21 21 l l ll b mm b pb pb yy , 2 21 1 xx and 1 2 21 b mm b pb pb yy . One can easily check that 2 21 2 1 12 ll xx and 1 22 22 2 12 () l ll mm pm pb bpb ll yyy , which verifies that our diagram commutes.  J. E. KALLIONGIS, R. OHASHI Copyright © 2012 SciRes. APM 165 Proposition 47. 0,pmn is a sublattice of 0, k pm n, and there exists a lattice surjection 00 :, , k pm npm n induced by the the family of group homomorphisms l such that restricted to 0,pm n is the identity. Proof. It is clear that 0,pm n is a sublattice of 0, k pm n. If 0 π,, k bdpmn, then l bpb for some lk . By Proposition 45, there exists a surjec- tion :π,π, l l nn pb pb . Define π,π, lnn pb pb . By the commutative dia- gram in Proposition 46, it follows that is order pre- serving. Theorem 48. Let 1 2i km j i i mp be the prime de- composition. Then 1 2, k j i ipn is a sublattice of 1 2, i km j i ipn , and there exists a lattice surjection 11 :2,2, i kk m jj ii ii pn pn induced by a family of group homomorphisms such that restricted to 1 2, k j i ipn is the identity. Proof. Apply 11 :2, 2, i ir ir m mm jj i r rr iri ik ik ppn ppn repeatedly defined in Proposition 47 for 1rk to obtain the result where is the compositions of those r ’s. 8. Some Examples In this section we present several examples which illus- trate the main theorems. Example 49. 1315,14. This example illustrates Theorem 12 that 1315,14 is isomorphic to 1315,14. Example 50. 11155,11. This is a Boolean lattice/ algebra by Proposition 36 since 1155357 11. Prime ideals are: 3,11 , 5,11 and 7,11 Their complements are lters which are: 35,11 , 21, 11 and 15,11 respectively. Example 51. 2126, 20. Since 200 (mod 4), this example illustrates Theorems 15 and 16 that 221 126,20126,2063,20 . Example 52. 25040,20. This example again illus- trates Theorem 16 and also that 25040,20 is iso- morphic to 2126, 20.  J. E. KALLIONGIS, R. OHASHI Copyright © 2012 SciRes. APM 166 Example 53. 25040,5. This illustrates Theorem 16 that 25040,5 is isomorphic to a disjoint union of isomorphic lattices 11 11 63,5126,5252,5504,5 . Example 54. 25040,10. This example illustrates Theorem 16 that 31 1 1263,5 63,10 j j . Example 55. 35030,10. This example illustrates Theorems 18 and 19 that 331 5030,105030,1063,2510 . Example 56. 4126,5. This example illustrates Theorem 21 that 41 126,10 126,5 . Example 57. 5630,5. This example illustrates Theorem 22 that 511 630,563,5126,5.  J. E. KALLIONGIS, R. OHASHI Copyright © 2012 SciRes. APM 167 Example 58. 55040,10. This example illustrates Theorem 22 that 511 5040,101008,55040,10 . Example 59. 663,5. This example illustrates Theo- rems 19 and 23 that 611 63,517, 2934, 29 . Example 60. 7126, 20. This illustrates Theorems 16 and 24 that 721 126,20126,2063,20 . 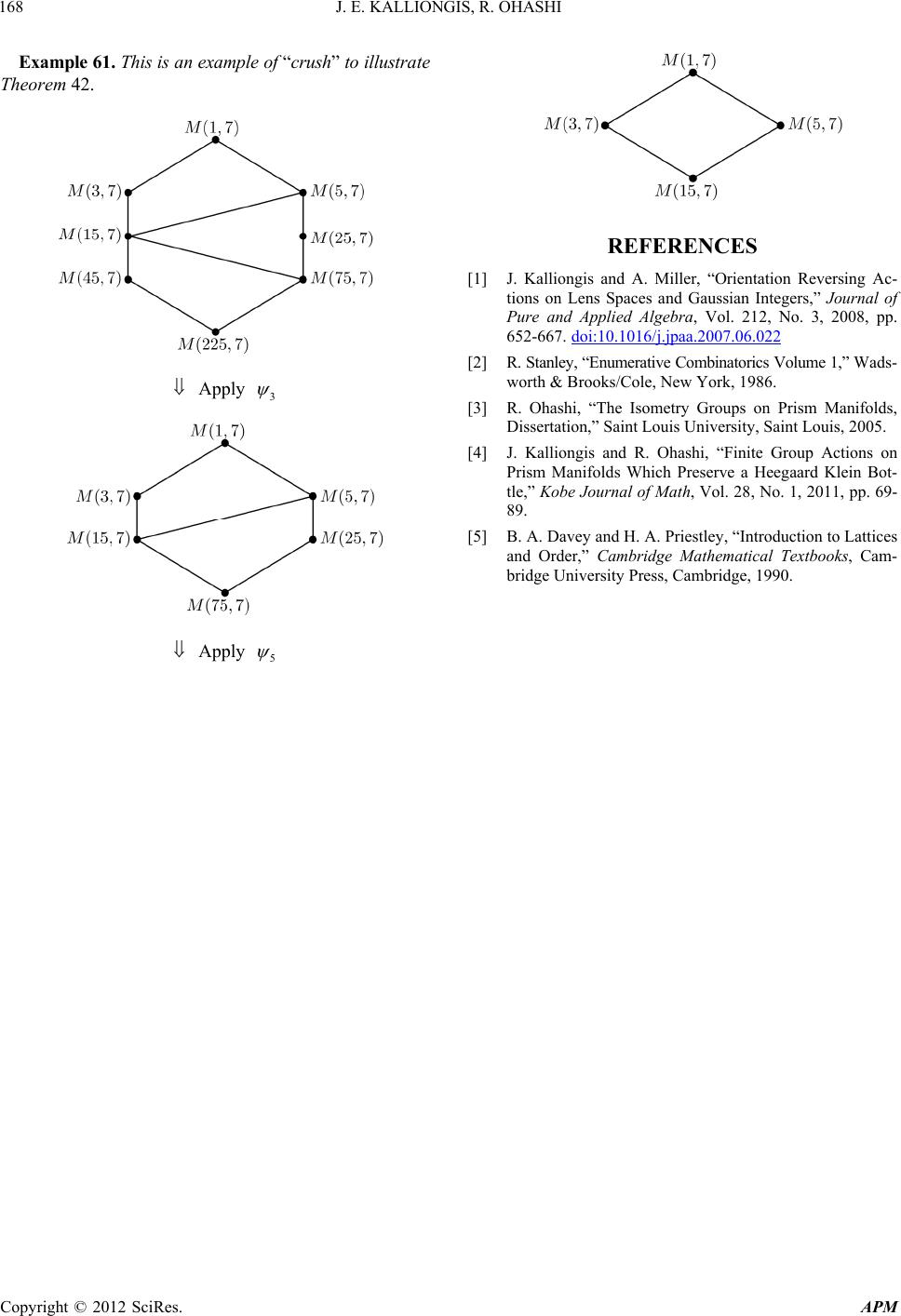 J. E. KALLIONGIS, R. OHASHI Copyright © 2012 SciRes. APM 168 Example 61. This is an example of “crush” to illustrate Theorem 42. Apply 3 Apply 5 REFERENCES [1] J. Kalliongis and A. Miller, “Orientation Reversing Ac- tions on Lens Spaces and Gaussian Integers,” Journal of Pure and Applied Algebra, Vol. 212, No. 3, 2008, pp. 652-667. doi:10.1016/j.jpaa.2007.06.022 [2] R. Stanley, “Enumerative Combinatorics Volume 1,” Wads- worth & Brooks/Cole, New York, 1986. [3] R. Ohashi, “The Isometry Groups on Prism Manifolds, Dissertation,” Saint Louis University, Saint Louis, 2005. [4] J. Kalliongis and R. Ohashi, “Finite Group Actions on Prism Manifolds Which Preserve a Heegaard Klein Bot- tle,” Kobe Journal of Math, Vol. 28, No. 1, 2011, pp. 69- 89. [5] B. A. Davey and H. A. Priestley, “Introduction to Lattices and Order,” Cambridge Mathematical Textbooks, Cam- bridge University Press, Cambridge, 1990.
|