Open Journal of Statistics
Vol.1 No.2(2011), Article ID:6183,13 pages DOI:10.4236/ojs.2011.12014
Runs and Patterns in a Sequence of Markov Dependent Bivariate Trials
Department of Statistics, School of Mathematical Sciences, North Maharashtra University, Jalgaon, India
E-mail: kirteekamalja@gmail.com
Received May 13, 2011; revised June 2, 2011; accepted June 8, 2011
Keywords: Markov Dependent Bivariate Trials, Conditional Probability Generating Function, Joint Distribution
Abstract
In this paper we consider a sequence of Markov dependent bivariate trials whose each component results in an outcome success (0) and failure (1) i.e. we have a sequence  of
of  valued Markov dependent bivariate trials. By using the method of conditional probability generating func-tions (pgfs), we derive the pgf of joint distribution of
valued Markov dependent bivariate trials. By using the method of conditional probability generating func-tions (pgfs), we derive the pgf of joint distribution of  where for
where for ,
,  de-notes the number of occurrences of i-runs of length
de-notes the number of occurrences of i-runs of length  in the first component and
in the first component and  denotes the number of occurrences of i-runs of length
denotes the number of occurrences of i-runs of length  in the second component of Markov dependent bivariate trials. Further we consider two patterns
in the second component of Markov dependent bivariate trials. Further we consider two patterns  and
and  of lengths
of lengths  and
and  respectively and obtain the pgf of joint distribution of
respectively and obtain the pgf of joint distribution of  using method of conditional probability generating functions where
using method of conditional probability generating functions where  denotes the number of occurrences of pattern
denotes the number of occurrences of pattern  of length
of length  in the first (second) n components of bivariate trials. An algorithm is developed to evaluate the exact probability distributions of the vector random variables from their derived probability generating functions. Further some waiting time distributions are studied using the joint distribution of runs.
in the first (second) n components of bivariate trials. An algorithm is developed to evaluate the exact probability distributions of the vector random variables from their derived probability generating functions. Further some waiting time distributions are studied using the joint distribution of runs.
1. Introduction
The distributions of several run statistics are used in various areas such as reliability theory, testing of statistical hypothesis, DNA sequencing, psychology [1], start up demonstration tests [2] etc. There are various counting schemes of runs. Some of the most popular counting schemes of runs are non-overlapping success runs of length 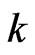 [3], overlapping success runs of length
[3], overlapping success runs of length  [4], success runs of length at least
[4], success runs of length at least ,
,  - overlapping success runs of length
- overlapping success runs of length  [5], success runs of exact length
[5], success runs of exact length  [6].
[6].
The probability distribution of various run statistics associated with the above counting schemes have been studied extensively in the literature in different situations such as independent Bernoulli trials (BT), non-identical BT, Markov dependent BT (MBT), higher order MBT, binary sequence of order , multi-state trials etc. But very little work is found on the distribution theory of run statistics in case of bivariate trials which has applications in different areas such as start up demonstration tests with regard to simultaneous start ups of two equipment, reliability theory of two dimensional consecutive
, multi-state trials etc. But very little work is found on the distribution theory of run statistics in case of bivariate trials which has applications in different areas such as start up demonstration tests with regard to simultaneous start ups of two equipment, reliability theory of two dimensional consecutive  out of
out of :
:  -Lattice system etc as specified by [7]. [7] have studied the distribution of sooner and later waiting time problems for runs in Markov dependent bivariate trials by giving system of linear equations of the conditional pgfs of the waiting times. The distribution of number of occurrences of runs in the two components of bivariate sequence of trials and their joint distributions are still unknown to the literature.
-Lattice system etc as specified by [7]. [7] have studied the distribution of sooner and later waiting time problems for runs in Markov dependent bivariate trials by giving system of linear equations of the conditional pgfs of the waiting times. The distribution of number of occurrences of runs in the two components of bivariate sequence of trials and their joint distributions are still unknown to the literature.
Consider a sequence  of
of  -valued trials where
-valued trials where  is set of all possible outcomes of trials under study. The simple pattern
is set of all possible outcomes of trials under study. The simple pattern  is composed of specified sequence of
is composed of specified sequence of  states i.e.
states i.e.  where
where . The number of occurrences of patterns can be counted according to the non-overlapping or overlapping counting scheme. The non-overlapping counting scheme starts recounting of the pattern immediately after the occurrence of the pattern while the overlapping counting scheme of patterns allows an overlap of prespecified fixed length in the successive occurrences of patterns.
. The number of occurrences of patterns can be counted according to the non-overlapping or overlapping counting scheme. The non-overlapping counting scheme starts recounting of the pattern immediately after the occurrence of the pattern while the overlapping counting scheme of patterns allows an overlap of prespecified fixed length in the successive occurrences of patterns.
Recently the study of distributions of different statistics based on patterns has become a focus area for many researchers due to its wide applicability area. Distribution of , the waiting time for the
, the waiting time for the  occurrence of pattern
occurrence of pattern  of length
of length  in the sequence of multistate trials is studied by [1,8,9]. [10] considered the sequence
in the sequence of multistate trials is studied by [1,8,9]. [10] considered the sequence  generated by Polya’s urn scheme and study the waiting time distribution of
generated by Polya’s urn scheme and study the waiting time distribution of  for
for .
.
Joint distribution of number of occurrences of pattern  of length
of length  and pattern
and pattern  of length
of length  in
in  Markov dependent multi-state trials is studied by [11]. [12] considered a sequence
Markov dependent multi-state trials is studied by [11]. [12] considered a sequence  of
of  - dimensional i.i.d. Random column vectors whose entries are
- dimensional i.i.d. Random column vectors whose entries are  -valued i.i.d. random variables and obtain the waiting time distribution of two dimensional patterns with general shape. The general method, which is an extension of method of conditional pgfs, is used to study these distributions by [12].
-valued i.i.d. random variables and obtain the waiting time distribution of two dimensional patterns with general shape. The general method, which is an extension of method of conditional pgfs, is used to study these distributions by [12].
Even though the distribution of waiting time of the pattern of general shape in the sequence of multi-variate trials with i.i.d. components has been done, the joint distribution of number of occurrences of patterns  in the sequence of
in the sequence of  component of the
component of the  -variate trials
-variate trials  is still unknown. Here we derive the pgf of joint distribution of number of occurrences of runs in both the components of the bivariate trials and generalize this study to the distribution of number of occurrences of patterns in both components of the bivariate trials.
is still unknown. Here we derive the pgf of joint distribution of number of occurrences of runs in both the components of the bivariate trials and generalize this study to the distribution of number of occurrences of patterns in both components of the bivariate trials.
In this paper we consider the sequence  of
of  -valued Markov dependent bivariate trials. In Section 2, we obtain the pgf of joint distribution of number of occurrences of
-valued Markov dependent bivariate trials. In Section 2, we obtain the pgf of joint distribution of number of occurrences of  -runs of length
-runs of length  in first components and
in first components and  -runs of length
-runs of length  in the second components of the bivariate trials
in the second components of the bivariate trials . We study this joint distribution of runs under the non-overlapping counting scheme of runs by using the method of conditional pgfs. Further in section 3, we study the joint distribution of number of occurrences of pattern
. We study this joint distribution of runs under the non-overlapping counting scheme of runs by using the method of conditional pgfs. Further in section 3, we study the joint distribution of number of occurrences of pattern  of length
of length  in the first component and number of occurrences of pattern
in the first component and number of occurrences of pattern 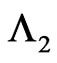 of length
of length  in the second component of bivariate trials. In Section 4, we develop an algorithm to evaluate the exact probability distributions of the random variables under study. As an application of the derived joint distributions, in Section 5, we obtain distributions of several waiting times associated with the runs and patterns in bivariate trials. In Section 6 we present some numerical work based on distribution of runs and patterns. Finally in Section 7, we discuss an application and generalization of the studied distributions.
in the second component of bivariate trials. In Section 4, we develop an algorithm to evaluate the exact probability distributions of the random variables under study. As an application of the derived joint distributions, in Section 5, we obtain distributions of several waiting times associated with the runs and patterns in bivariate trials. In Section 6 we present some numerical work based on distribution of runs and patterns. Finally in Section 7, we discuss an application and generalization of the studied distributions.
2. The Joint Distribution of Number of Occurrences of Runs
Let . Consider the sequence
. Consider the sequence  of
of  -valued Markov dependent bivariate trials with the transition probabilities,
-valued Markov dependent bivariate trials with the transition probabilities,

and the initial probabilities
 for
for .
.
Let  be the number of
be the number of  -runs (
-runs ( = 0,1) of length
= 0,1) of length 
 in
in  trials associated with the first (second) component of bivariate trials (i.e. number of
trials associated with the first (second) component of bivariate trials (i.e. number of  -runs in
-runs in . In this section we derive the joint distribution of
. In this section we derive the joint distribution of
 .
.
Let  be the pgf of distribution of
be the pgf of distribution of
 . Assume that for a non-negative integer
. Assume that for a non-negative integer , we have observed until
, we have observed until  trial
trial
(i.e. we have observed ). We define
). We define  as pgf of conditional distribution of number of
as pgf of conditional distribution of number of  -runs of length
-runs of length  in
in  and number of
and number of  -runs of length
-runs of length  in
in  given that we have observed
given that we have observed
 and currently have
and currently have  -run of length
-run of length  in first component and
in first component and  -runs of length
-runs of length  in the second component of bivariate trials is observed,
in the second component of bivariate trials is observed,  ,
,  ,
, 
We define  for
for .
.
Now by assuming , we have,
, we have,
 (2.1)
(2.1)
Also we have,
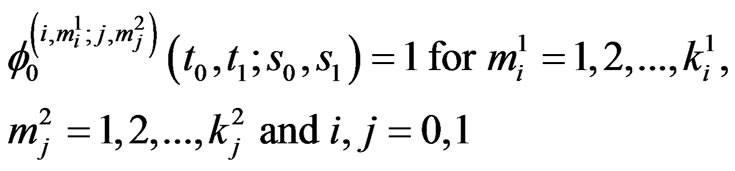 (2.2)
(2.2)
Conditioning on the first trial we have the following system of recurrent relation of conditional pgfs for .
.

Conditioning on the next trial from each stage, we have the following system of recurrent relations of conditional pgfs for  and
and .
.
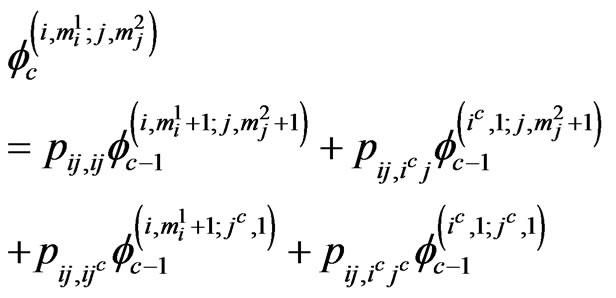
if ,
,  ,
,

if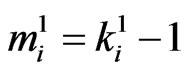 ,
,  ,
,

if ,
, 

if ,
,  ,
,

if ,
,  ,
,

if ,
,  ,
,

if ,
,  ,
,

if ,
, 
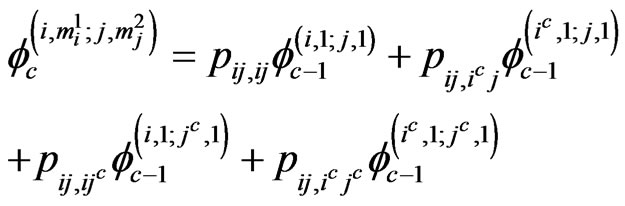
if ,
, 
Thus we have  recurrent relations of conditional pgfs for
recurrent relations of conditional pgfs for  and these can be written as,
and these can be written as,
 (2.3)
(2.3)
where
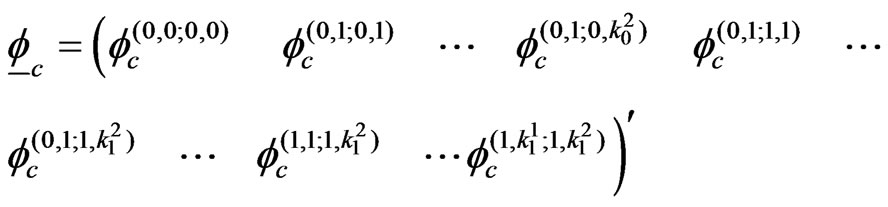
and  is a square matrix of size
is a square matrix of size . Each row of this matrix corresponds to corresponding element of
. Each row of this matrix corresponds to corresponding element of  and its elements are the coefficients of elements of
and its elements are the coefficients of elements of .
.
For , we have,
, we have,

where  is the column vector with all the elements equal to 1.
is the column vector with all the elements equal to 1.
Using (2.3) recurrently for , we have,
, we have,
 (2.4)
(2.4)
Hence from (2.1) and (2.4) we get the pgf of distribution of  as,
as,
 (2.5)
(2.5)
where  is the first column of identity matrix of order
is the first column of identity matrix of order
 .
.
3. The Joint Distribution of Number of Occurrences of Patterns
Let  and
and  be two patterns of lengths
be two patterns of lengths  and
and  respectively where
respectively where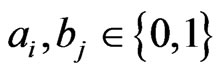 ,
, . We consider the non-overlapping counting scheme of patterns in which to count the number of occurrences of pattern
. We consider the non-overlapping counting scheme of patterns in which to count the number of occurrences of pattern  in a given sequence of
in a given sequence of  trials, one has to restart counting from scratch each time the pattern
trials, one has to restart counting from scratch each time the pattern  occurs. Let
occurs. Let  denotes the number of non-overlapping occurrences of patterns
denotes the number of non-overlapping occurrences of patterns  in the first component of
in the first component of  bivariate trials (i.e. in
bivariate trials (i.e. in ) and
) and  denotes the number of non-overlapping occurrences of patterns
denotes the number of non-overlapping occurrences of patterns  in the second component of
in the second component of  bivariate trials (i.e. in
bivariate trials (i.e. in ). Consider the random vector
). Consider the random vector . In this section we obtain the pgf of joint distribution of
. In this section we obtain the pgf of joint distribution of  using method of conditional pgfs.
using method of conditional pgfs.
Let pgf of joint distribution of  be
be . Assume that for a non-negative integer
. Assume that for a non-negative integer , we have observed until
, we have observed until  trial i.e.
trial i.e.
 . For
. For , we define, the following conditional pgfs.
, we define, the following conditional pgfs.
Let  be pgf of conditional distribution of number of occurrences of patterns
be pgf of conditional distribution of number of occurrences of patterns  in
in  and number of occurrences of pattern
and number of occurrences of pattern  in
in  of bivariate trials given that currently (i.e. at
of bivariate trials given that currently (i.e. at  trial) we have observed none of the subpatterns of
trial) we have observed none of the subpatterns of  and
and  and
and , where
, where .
.
Similarly let,  be pgf of conditional distribution of number of occurrences of patterns
be pgf of conditional distribution of number of occurrences of patterns  in
in  and patterns
and patterns 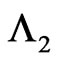 in
in  of bivariate trials given that at
of bivariate trials given that at  trial we have observed the sub-pattern of length
trial we have observed the sub-pattern of length  of
of  in the first component and none of the sub pattern of
in the first component and none of the sub pattern of  is observed in the second component of bivariate trials and
is observed in the second component of bivariate trials and
 where
where  and
and .
.
Let  be pgf of conditional distribution of number of occurrences of patterns
be pgf of conditional distribution of number of occurrences of patterns  in
in  and patterns
and patterns  in
in  of bivariate trials given that at
of bivariate trials given that at  trial we have observed none of the sub-pattern of
trial we have observed none of the sub-pattern of  in the first component and a sub pattern of the length
in the first component and a sub pattern of the length  of
of  in the second component of bivariate trials is observed and
in the second component of bivariate trials is observed and  where
where  and
and .
.
Also let  as pgf of conditional distribution of number of occurrences of pattern
as pgf of conditional distribution of number of occurrences of pattern  in
in 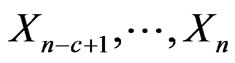 and pattern
and pattern  in
in  of bivariate trials given that at
of bivariate trials given that at  trial we have observed the sub-pattern of length
trial we have observed the sub-pattern of length  of
of  in the first component and a sub pattern of the length
in the first component and a sub pattern of the length  of
of  in the second component of bivariate trials and
in the second component of bivariate trials and  where
where
 and
and .
.
Let,
 ,
, 
and ,
, .
.
For , we assume that at
, we assume that at  trial, the sub-pattern of length
trial, the sub-pattern of length  of
of  is observed in the first component of bivariate trials. If we condition on the next trial as
is observed in the first component of bivariate trials. If we condition on the next trial as  i.e. the sub-pattern of length
i.e. the sub-pattern of length  of
of  observed at
observed at  trial breaks at
trial breaks at  trial then to check whether any sub-pattern of
trial then to check whether any sub-pattern of  of length
of length  has occurred, we define the indicator function
has occurred, we define the indicator function  as,
as,

 .
.
Similarly we have indicator function  as,
as,

 .
.
Let
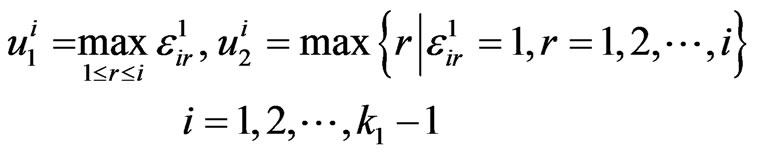 ,
,

Assuming , we have,
, we have,
 (3.1)
(3.1)
We also have,


 .(3.2)
.(3.2)
Now for each  (
( denotes the number of trials remaining to observe) we condition on the next trial to obtain the recurrent relations of conditional pgfs as follows.
denotes the number of trials remaining to observe) we condition on the next trial to obtain the recurrent relations of conditional pgfs as follows.

if ,
,

if 

if 

if .
.
Similarly we have recurrent relations of the conditional pgfs  for
for  as follows.
as follows.

if 

if 

if 
The recurrent relations of the conditional pgfs  for
for  and
and  are as follows.
are as follows.

if 

if 














The above system of  recurrent relations of conditional pgfs
recurrent relations of conditional pgfs ,
, ;
;
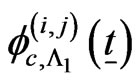 ,
, ;
; ,
,
 and
and 
 can be written as follows.
can be written as follows.
 (3.3)
(3.3)
where  is column vector with all its elements 1 and
is column vector with all its elements 1 and  is column vector with its elements as follows.
is column vector with its elements as follows.

From (3.1) we get,

where  is first column of identity matrix of order
is first column of identity matrix of order .
.
The recurrent use of (3.3) gives the pgf of  as follows.
as follows.
 (3.4)
(3.4)
4. Exact distribution of 
We note that the pgf of  is a particular case of pgf of
is a particular case of pgf of . Hence we develop an algorithm to obtain the exact probability distribution of
. Hence we develop an algorithm to obtain the exact probability distribution of  which can further beapplied to obtain the exact probability distribution of
which can further beapplied to obtain the exact probability distribution of  from its pgf.
from its pgf.
Observe that the pgf of joint distribution of  as obtained in (2.5) in general involves matrix polynomial
as obtained in (2.5) in general involves matrix polynomial  in
in ,
, ,
, and
and  of order n where
of order n where
 .
.
Hence the joint probability distribution can be obtained by expanding the polynomial with respect to ,
, ,
, and
and .
.
That is,

i.e.
 (4.1)
(4.1)
Exact formula to obtain the coefficient matrix is quiet tedious since multiplication of matrices is not commutative operation. But the interesting recurrent relations are found between these coefficient matrices. Let
 be the coefficient matrix of
be the coefficient matrix of
 in the expansion of matrix polynomial
in the expansion of matrix polynomial  and for
and for , let
, let
 . The following Lemma gives the recurrent relations of the coefficient matrices of
. The following Lemma gives the recurrent relations of the coefficient matrices of  with
with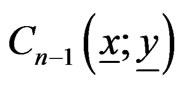 .
.
Lemma 4.1 Let  be the coefficient matrix of
be the coefficient matrix of  in the expansion of the matrix polynomial
in the expansion of the matrix polynomial
 Then
Then  satisfies the following recurrent relation.
satisfies the following recurrent relation.
 (4.2)
(4.2)
with ,
,  ,
,  and
and  for
for . Here
. Here  is the
is the  row of the identity matrix of order 2.
row of the identity matrix of order 2.
Proof Obviously for , we have,
, we have,

where O is the null matrix of same order as that of A.
For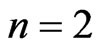 , observe that
, observe that  satisfies (4.2).
satisfies (4.2).
Assume that Equation (4.2) is true for some .
.
Hence we have,

Then

Hence we get the required proof of the lemma.
Theorem 4.1 The exact probability distribution of  is given by,
is given by,
 ,(4.3)
,(4.3)
where  is the coefficient matrix of
is the coefficient matrix of  in expansion of matrix polynomial
in expansion of matrix polynomial  and it satisfies (4.2)
and it satisfies (4.2)
Proof The proof follows by applying the Lemma 4.1 to matrix polynomial  involved in the pgf of distribution of
involved in the pgf of distribution of  in (2.5).
in (2.5).
Remark 4.1 The expected number of failure-runs of length  in first components of
in first components of  Markov dependent bivariate trials is given by,
Markov dependent bivariate trials is given by,
 .
.
On simplifying this expression, we have,
 (4.4)
(4.4)
5. Waiting Time Distributions Related to Runs and Patterns
The exact probability distribution of  from its pgf given in (2.5) can be expressed as,
from its pgf given in (2.5) can be expressed as,
 (5.1)
(5.1)
The components of the above expression can be interpreted as follows.

For ,
,
 and
and
 .
.
Similarly for ,
,
 (5.2)
(5.2)
so that
 (5.3)
(5.3)
The above interpretation is useful for deriving different waiting time distributions.
Let  be the event that failure-run of length
be the event that failure-run of length  occur for the first time in the
occur for the first time in the  component of the Markov dependent bivariate trials and
component of the Markov dependent bivariate trials and  be the event that success-run of length
be the event that success-run of length  occur for the first time in the
occur for the first time in the  component of the Markov dependent bivariate trials
component of the Markov dependent bivariate trials .
.
Let  be the waiting time for sooner occurring event between
be the waiting time for sooner occurring event between ,
, 
 ,
, . To obtain the distribution of sooner waiting time we define the following random variables.
. To obtain the distribution of sooner waiting time we define the following random variables.
 : The waiting time for sooner occurring event between
: The waiting time for sooner occurring event between ,
, 
 ,
, given that
given that  is the sooner event (i.e.
is the sooner event (i.e.  -run of length
-run of length  of
of  component of bivariate trials is the sooner event)
component of bivariate trials is the sooner event)  and
and .
.
 : The waiting time for the first occurrence of
: The waiting time for the first occurrence of  -run of length
-run of length  in the
in the  component of the bivariate trials
component of the bivariate trials ,
,  and
and .
.
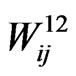 : The waiting time until the occurrence of both events
: The waiting time until the occurrence of both events  and
and  simultaneously,
simultaneously,  (i.e.
(i.e.  - run of length
- run of length  in the first component and
in the first component and  -run of length
-run of length  in the second component of the bivariate trials occur simultaneously).
in the second component of the bivariate trials occur simultaneously).
Then we have,
 .(5.4)
.(5.4)
Let ,
,  ,
,  and
and  be the pgf of
be the pgf of ,
,  ,
,  and
and ,
,  and
and  respectively. In the next sub-section we obtain the sooner waiting time distribution.
respectively. In the next sub-section we obtain the sooner waiting time distribution.
5.1. Sooner Waiting Time Distribution
The probability that 0-run of length  (i.e. event
(i.e. event ) occurs for the first time at
) occurs for the first time at  trial given that none of the events
trial given that none of the events 
 ,
,  has occurred until
has occurred until  trial
trial  can be written as follows.
can be written as follows.

Hence pgf of  can be given as,
can be given as,
 .
.
Similarly the probability that 1-run of length  (i.e. event
(i.e. event ) occurs for the first time at
) occurs for the first time at  trial given that none of the events
trial given that none of the events 
 ,
,  has occurred until
has occurred until  trial
trial  can be written as follows.
can be written as follows.

Hence pgf of  is,
is,
 .
.
Similarly  and
and  is given by,
is given by,


and pgf of  is,
is,
 .
.
Now the probability that both events  and
and 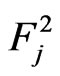 occurs simultaneously for the first time at
occurs simultaneously for the first time at  trial
trial
 can be written as follows.
can be written as follows.




In general,

Also pgf of  is,
is,

Hence from (5.4), the exact probability distribution of random variable  is given by,
is given by,
 ,
,  .(5.5)
.(5.5)
The pgf of  is given by,
is given by,
 (5.6)
(5.6)
Here we note that it is quiet difficult to study the later waiting time distribution between ,
, 
 ,
, , particularly when one is interested in studying the waiting time distribution for the later occurring event between more than two events. For the waiting time distribution of later occurring event between any two runs in the components of the bivariate trials or for the two patterns in the two components of bivariate trials the theory can be developed in general. For this we refer [13] who derive the waiting time distribution of later occurring event between the two events
, particularly when one is interested in studying the waiting time distribution for the later occurring event between more than two events. For the waiting time distribution of later occurring event between any two runs in the components of the bivariate trials or for the two patterns in the two components of bivariate trials the theory can be developed in general. For this we refer [13] who derive the waiting time distribution of later occurring event between the two events  and
and  where
where 
 is the event that
is the event that  -run of length
-run of length  occurs for the first time in the sequence of higher order Markov dependent BT. [13] use the joint distribution of number of occurrences of 1-runs (i.e. success-runs) of length
occurs for the first time in the sequence of higher order Markov dependent BT. [13] use the joint distribution of number of occurrences of 1-runs (i.e. success-runs) of length  and the number of occurrences of 0-runs (i.e. failure runs) of length
and the number of occurrences of 0-runs (i.e. failure runs) of length .
.
5.2. Waiting Time Distribution for Runs
Let  be the waiting time for the
be the waiting time for the  occurrence of
occurrence of  -run of length
-run of length  for the
for the  component of bivariate trials,
component of bivariate trials, ;
; . We obtain the distribution of
. We obtain the distribution of
 using distribution of
using distribution of  number of occurrences of
number of occurrences of 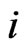 -run of length
-run of length  for the
for the  component of
component of  bivariate trials
bivariate trials ;
; . The pgf
. The pgf 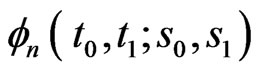 of joint distribution of
of joint distribution of
 as obtained in (2.5) is as follows.
as obtained in (2.5) is as follows.

In particular pgf of marginal distribution of  is obtained by setting
is obtained by setting  in the pgf
in the pgf
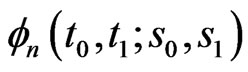 of
of  and is as follows.
and is as follows.
 (5.7)
(5.7)
Let pgf of  be
be  for
for ;
; . Then pgf of
. Then pgf of  in (5.7) can be expressed in a simplified form as follows.
in (5.7) can be expressed in a simplified form as follows.

where  and
and .
.
The exact probability distribution of  can be obtained from Lemma 4.1 as follows.
can be obtained from Lemma 4.1 as follows.
 (5.8)
(5.8)
where 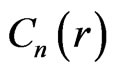 is the coefficient matrix of
is the coefficient matrix of  in the matrix polynomial
in the matrix polynomial  and in general for
and in general for 
 satisfies the recurrent relation
satisfies the recurrent relation

with 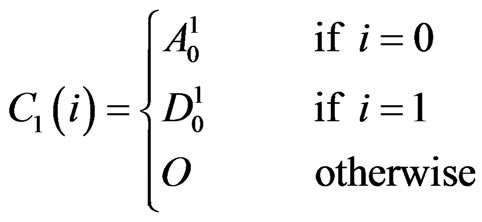
where 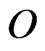 is the null matrix of order same as matrix
is the null matrix of order same as matrix  and
and . The probability in (5.8) can be written as follows.
. The probability in (5.8) can be written as follows.

The above components of  can be interpreted as follows.
can be interpreted as follows.

 (5.9)
(5.9)
Now we have,

Using the pgf of  and interpretations in (5.9) we have,
and interpretations in (5.9) we have,

Particularly when , we have,
, we have,

The pgf of  is given by,
is given by,

and formula for exact probability is
 ,
, .
.
Similarly waiting time distributions of ,
,  and
and  can be obtained.
can be obtained.
6. Numerical Study
In this section we present the numerical study based on the joint distribution of patterns in the sequence of bivariate trials. We consider the sequence
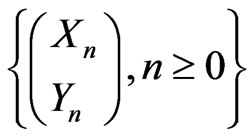 of
of  -valued Markov dependent bivariate trials with
-valued Markov dependent bivariate trials with  with transition probabilities as follows.
with transition probabilities as follows.
 ,
, ,
, ,
,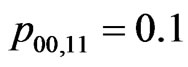 ,
,
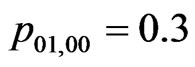 ,
, ,
, ,
, ,
,
 ,
, ,
, ,
, ,
,
 ,
, ,
, ,
, 
Let  and
and . The joint distribution of
. The joint distribution of  is evaluated numerically for
is evaluated numerically for  using the algorithm given in Theorem 4.1. The evaluated joint pmf of
using the algorithm given in Theorem 4.1. The evaluated joint pmf of  is described in the following Table 1.
is described in the following Table 1.
7. Application and Extension
[14] introduced the two-dimensional engineering system consisting of a grid of  components arranged in
components arranged in  -rows and
-rows and  -columns. The system and its components can be either in working or failed state. The system fails if and only if a grid of size
-columns. The system and its components can be either in working or failed state. The system fails if and only if a grid of size  components fails. Particularly, for
components fails. Particularly, for , we can formulate the states of the components in this system as a sequence of
, we can formulate the states of the components in this system as a sequence of  independent bivariate trials. We assume that the
independent bivariate trials. We assume that the  component in a column is in state 1 if it is in failed state and in state 0 otherwise. For
component in a column is in state 1 if it is in failed state and in state 0 otherwise. For  we define,
we define,
 and
and

The reliability of consecutive- -out-of-
-out-of- :
:
F-Lattice system can now be obtained simply by using the joint distribution of  asP(consecutive-
asP(consecutive- -out-of-
-out-of- : F-Lattice system works) =
: F-Lattice system works) = where
where  is 1-run of length
is 1-run of length  in the first component and
in the first component and  is 1-run of length
is 1-run of length  in the second component of the bivariate trials.
in the second component of the bivariate trials.
Extending the concept of bivariate trials to multivariate trials, the joint distributions of number of occurrences of patterns  of length
of length 
 in the
in the  component of
component of  -variate trials can be used to get the reliability of general two-dimensional consecutive-
-variate trials can be used to get the reliability of general two-dimensional consecutive-  -out-of-
-out-of- : F-Lattice system.
: F-Lattice system.

Table 1. Distribution of .
.
The pgf  of joint distribution of
of joint distribution of , the number of occurrences of patterns
, the number of occurrences of patterns  of length
of length  in the
in the  component of
component of  -variate trials obtained in general by using the method of conditional pgfs is of form,
-variate trials obtained in general by using the method of conditional pgfs is of form,

(7.1)
Extending the Lemma 4.1 for the pgf in (7.1) exact joint probability distribution of  can be obtained.
can be obtained.
The above study of runs and patterns can be extended in another direction by generalizing the sequence of Markov dependent bivariate trials to the sequence of Markov dependent multivariate trials. In the following, we discuss briefly the method of deriving the joint distribution of  where
where ,
,
 denotes the number of occurrences of two dimensional patterns of rectangular shape
denotes the number of occurrences of two dimensional patterns of rectangular shape 
 in the sequence of Markov dependent multivariate trials.
in the sequence of Markov dependent multivariate trials.
Let 
so that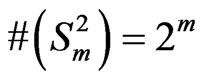 . Consider the sequence of
. Consider the sequence of  -variate
-variate  -valued Markov dependent trials
-valued Markov dependent trials . Let the transition probabilities of these Markov dependent trials
. Let the transition probabilities of these Markov dependent trials  be,
be,
 ,
,  ,
, .
.
and initial probabilities be .
.
Consider the two dimensional pattern of rectangular shape, 
 where
where . Let
. Let ,
,  be the number of occurrences of patterns
be the number of occurrences of patterns  in n trials
in n trials . We obtain the joint distribution of
. We obtain the joint distribution of
 using the method for deriving joint distribution of number of occurrences of patterns
using the method for deriving joint distribution of number of occurrences of patterns 
 in the sequence of multi-state trials as done by [11]. For this consider the following transformation of sequence of
in the sequence of multi-state trials as done by [11]. For this consider the following transformation of sequence of  -variate sequence of
-variate sequence of  -valued Markov dependent trials
-valued Markov dependent trials  to the univariate sequence of Markov dependent trials
to the univariate sequence of Markov dependent trials .
.
Define the function  such that
such that
 where
where . Hence
. Hence
 . Each
. Each 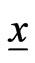 in
in  can be treated as a
can be treated as a  -digit binary number. The function
-digit binary number. The function  converts this
converts this  -digit binary number into a unique equivalent decimal number in
-digit binary number into a unique equivalent decimal number in .
.
Now corresponding to the  -variate sequence of
-variate sequence of  -valued Markov dependent trials
-valued Markov dependent trials , we have the univariate sequence of
, we have the univariate sequence of  -valued Markov dependent trials
-valued Markov dependent trials  where
where . The transition probabilities for the sequence of trials
. The transition probabilities for the sequence of trials  and for the converted sequence of trials
and for the converted sequence of trials 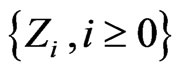 are related as follows.
are related as follows.

where  and
and . Convert the pattern
. Convert the pattern 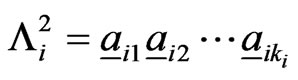
 into a pattern
into a pattern
 where
where  for
for . Now the original problem of studying the joint distribution of
. Now the original problem of studying the joint distribution of  in the sequence of
in the sequence of
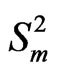 -valued Markov dependent trials
-valued Markov dependent trials 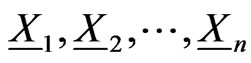 reduces to the problem of studying distribution of
reduces to the problem of studying distribution of
 for the sequence of
for the sequence of
 -valued Markov dependent trials
-valued Markov dependent trials . [15] obtain the joint distribution of number of occurrences of
. [15] obtain the joint distribution of number of occurrences of  -runs
-runs  of length
of length , while [11] obtain the joint distribution of number of occurrences of patterns in the sequence of
, while [11] obtain the joint distribution of number of occurrences of patterns in the sequence of  -valued Markov dependent trials using the method of conditional pgfs. The related waiting time distributions can also be studied following the same process as in Section 5 in the case of Markov dependent multivariate trials.
-valued Markov dependent trials using the method of conditional pgfs. The related waiting time distributions can also be studied following the same process as in Section 5 in the case of Markov dependent multivariate trials.
7. References
[1] S. J. Schwager, “Run Probabilities in Sequences of Markov-Dependent Trials,” Journal of American Statistical Association, Vol. 78, No. 381, 1983, pp. 168-175. doi:10.2307/2287125
[2] N. Balakrishnan and P. S. Chan, “Start-up Demonstration Tests with Rejection of Units upon Observing d Failures,” Annals of Institute of Statistical Mathematics, Vol. 52, No. 1, 2000, pp. 184-196. doi:10.1023/A:1004101402897
[3] W. Feller, “An Introduction to Probability Theory and Its Applications,” 3rd Edition, John Wiley & Sons, Hoboken, 1968.
[4] K. D. Ling, “On Binomial Distributions of Order k,” Statistics & Probability Letters, Vol. 6, No. 4, 1988, pp. 247-250. doi:10.1016/0167-7152(88)90069-7
[5] S. Aki and K. Hirano, “Number of Success-Runs of Specified Length until Certain Stopping Time Rules and Generalized Binomial Distributions of Order k,” Annals of Institute of Statistical Mathematics, Vol. 52, No. 4, 2000, pp. 767-777. doi:10.1023/A:1017585512412
[6] A. M. Mood, “The Distribution Theory of Runs,” Annals of Mathematical Statistics, Vol. 11, No. 4, 1940, pp. 367-392. doi:10.1214/aoms/1177731825
[7] S. Aki and K. Hirano, “Sooner and Later Waiting Time Problems for Runs in Markov Dependent Bivariate Trials,” Annals of Institute of Statistical Mathematics, Vol. 51, No. 1, 1999, pp. 17-29. doi:10.1023/A:1003874900507
[8] M. Uchida, “On Generating Functions of Waiting Time Problems for Sequence Patterns of Discrete Random Variables,” Annals of Institute of Statistical Mathematics, Vol. 50, No. 4, 1998, pp. 655-671. doi:10.1023/A:1003756712643
[9] D. L. Antzoulakos, “Waiting Times for Patterns in a Sequence of Multistate Trials,” Journal of Applied Probability, Vol. 38, No. 2, 2001, pp. 508-518. doi:10.1239/jap/996986759
[10] K. Inoue and S. Aki, “Generalized Waiting Time Problems Associated with Pattern in Polya’s Urn Scheme,” Annals of Institute of Statistical Mathematics, Vol. 54, No. 3, 2002, pp. 681-688. doi:10.1023/A:1022431631697
[11] K. S. Kotwal and R. L. Shinde, “Joint Distributions of Patterns in the Sequence of Markov Dependent MultiState Trials,” 2011 Submitted.
[12] S. Aki and K. Hirano, “Waiting Time Problems for a Two-Dimensional Pattern,” Annals of Institute of Statistical Mathematics, Vol. 56, No. 1, 2004, 169-182. doi:10.1007/BF02530530
[13] K. S. Kotwal and R. L. Shinde, “Joint Distributions of Runs in a Sequence of Higher-Order Two-State Markov trials,” Annals of Institute of Statistical Mathematics, Vol. 58, No. 1, 2006, pp. 537-554. doi:10.1007/s10463-005-0024-6
[14] A. A. Salvia and W. C. Lasher, “2-Dimensional Consecutive k-out-of-n: F Models,” IEEE Transactions on Reliability, Vol. R-39, No. 3, 1990, pp. 382-385. doi:10.1109/24.103023
[15] R. L. Shinde and K. S. Kotwal, “On the Joint Distribution of Runs in the Sequence of Markov Dependent MultiState Trials,” Statistics & Probability Letters, Vol. 76, No. 10, 2006, pp. 1065-1074. doi:10.1016/j.spl.2005.12.005

