Necessary Conditions for Optimal Control of Diffusions with Hard Terminal State Restrictions ()
1. Introduction
The purpose of the present paper is to prove necessary conditions for the optimal control of certain types of control problems involving diffusions where hard end constraints on solutions occur. The books [1] and [2] contain introductions to the topic of optimal control of diffusions. Various types of maximum principles have been proved for problems of control of diffusions in case of no or soft terminal state restrictions, see e.g. [3] [4] [5] and [6] . Maximum principles for problem with hard terminal restrictions are proved for certain types of continuous time controlled diffusion problems in [7] . In that paper only the drift term contained controls. In this paper controls are allowed to enter also the diffusion term. Singular controls are not discussed, below we merely consider problems where the controls appearing may be said to be absolutely continuous with respect to Lebesgue measure. The restriction to such controls makes it harder to operate with hard terminal state restrictions. In fact, the case discussed in detail in this paper is the case where hard terminal restrictions are only placed on states governed by differential equations not containing a Brownian motion. The necessary condititions are stated in terms of “weak” variations, not strong ones (needleshaped ones). Brownian motions will only appear in differential equations of states unconstrained at the terminal time. The constrained states are, however, influenced by other states directly influenced by Brownian motions, so, below, necessary conditions are stated and proved for such problems. Because the states are stochastic, the state space is infinite dimensional, so to obtain necessary conditions, one must impose a condition amounting to demanding sufficient variability of the first order variations in the problem.
2. The Control Problem and the Statement of the Necessary Condition
Let 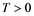 and let
and let 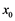 be a given point in the Euclidean space
be a given point in the Euclidean space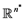 , let
, let 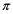 be a projection from
be a projection from 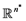 onto
onto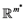 ,
, 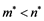 , such that
, such that 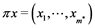
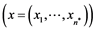 and let U be a closed convex subset of a Euclidean space
and let U be a closed convex subset of a Euclidean space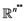 . The symbol
. The symbol  is used for the Euclidean norm in any Euclidean space
is used for the Euclidean norm in any Euclidean space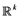 , including
, including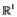 , and, applied to matrices, it is the linear operator norm. Furnish the interval
, and, applied to matrices, it is the linear operator norm. Furnish the interval 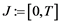 with the Lebesgue measure. Let
with the Lebesgue measure. Let 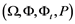 be a given filtered probability space, (i.e. for
be a given filtered probability space, (i.e. for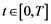 , the
, the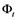 ’s are sub-s-algebras of the given s-algebra
’s are sub-s-algebras of the given s-algebra 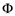 of subsets of
of subsets of![]() ,
, ![]() if
if![]() , P is a probability measure on
, P is a probability measure on![]() ), and assume that
), and assume that ![]() is complete, that
is complete, that ![]() contains all the P-null sets in
contains all the P-null sets in ![]() and that
and that ![]() is right continuous. Let
is right continuous. Let![]() ,
, ![]() , be the set of Lebesgue
, be the set of Lebesgue ![]() -measurable functions
-measurable functions ![]() for which
for which ![]() and let
and let ![]() be the subset of essentially bounded functions in
be the subset of essentially bounded functions in![]() . Related to
. Related to![]() , let
, let ![]() be a vector the
be a vector the ![]() components of which (denoted
components of which (denoted![]() ) are independent one-dimensional Brownian motions all adapted to
) are independent one-dimensional Brownian motions all adapted to![]() , such that
, such that ![]() is independent of
is independent of ![]() for all
for all![]() ,
, ![]() , and is normally distributed with mean 0 and covariances
, and is normally distributed with mean 0 and covariances![]() ,
, ![]() the identity matrix. In applications where the
the identity matrix. In applications where the![]() ’s are entities that can be observed, it is natural to take
’s are entities that can be observed, it is natural to take ![]() as the natural filtration generated by the
as the natural filtration generated by the![]() ’s. There are given functions
’s. There are given functions ![]() and
and ![]()
![]() , from
, from ![]() into
into![]() . Let
. Let ![]() be the set of functions
be the set of functions ![]() taking values in U, such that
taking values in U, such that![]() , for each t, when restricted to
, for each t, when restricted to![]() , is Borel
, is Borel ![]() -measurable (i.e. progressively measurable).
-measurable (i.e. progressively measurable).
Let ![]() be the
be the ![]() -norm both on
-norm both on ![]() and on
and on![]() .
.
The following conditions are called the Basic Assumptions.
A1 The functions ![]() and
and ![]() have derivatives
have derivatives ![]() and
and ![]() with respect to
with respect to![]() ,
, ![]() that are continuous in
that are continuous in![]() .
.
A2 As a function of t, the functions f and ![]() and their derivatives have one-sided limits with respect to t.
and their derivatives have one-sided limits with respect to t.
Write ![]() for the
for the ![]() -matrix whose columns are
-matrix whose columns are![]() , let
, let ![]() (
(![]() ) be the matrix with entries
) be the matrix with entries ![]() (
(![]() ), and write
), and write![]() . Also, write
. Also, write ![]() for the indicator function of the set C.
for the indicator function of the set C.
The following assumptions are called the Global Assumptions.
B1 ![]() and
and ![]() are uniformly continuous in
are uniformly continuous in![]() , uniformly in t.
, uniformly in t.
B2 For some constant M, for some given ![]() in
in![]() , for all
, for all![]() ,
,
![]() (1)
(1)
B3 A constant ![]() exists such that for all
exists such that for all![]() ,
,
![]() (2)
(2)
B4
![]() (3)
(3)
Let ![]() be the set of progressively measurable functions in
be the set of progressively measurable functions in![]() ,
,![]() . From now on we require that all control functions
. From now on we require that all control functions ![]() belong to
belong to![]() . The strong (unique) solution―continuous in t―of the equation
. The strong (unique) solution―continuous in t―of the equation
![]() (4)
(4)
is denoted![]() .
.
Let ![]() (a fixed,
(a fixed,![]() ) such that
) such that![]() , let
, let ![]() denote scalar product, and consider the problem
denote scalar product, and consider the problem
![]() (5)
(5)
subject to
![]() (6)
(6)
Below, ![]() will be an optimal control in this problem, assumed to exist. Write
will be an optimal control in this problem, assumed to exist. Write![]() .
.
We have collected a few definitions that are going to be used in the sequel.
For![]() , let
, let
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
where![]() . Let
. Let
![]() (12)
(12)
Finally, let
![]() (13)
(13)
![]() (14)
(14)
In the subsequent necessary conditions, the following local linear controllability condition (15) is needed. There exist numbers![]() ,
, ![]() and
and![]() , and a progressively measurable function
, and a progressively measurable function ![]() such that for all
such that for all ![]() for which
for which
![]() ,
,
![]() (15)
(15)
A more “concrete” condition implying (15) is presented in Remark 3.
Theorem 1. Assume that ![]() is optimal in problem (5),(6), that Assumptions A and B hold (the Basic and Global Assumptions) and that (15) is satisfied. Then the following necessary conditions hold: For some linear functional
is optimal in problem (5),(6), that Assumptions A and B hold (the Basic and Global Assumptions) and that (15) is satisfied. Then the following necessary conditions hold: For some linear functional ![]() on
on![]() , bounded on
, bounded on![]() , and some number
, and some number![]() , for all
, for all![]() ,
,
![]() (16)
(16)
where ![]() is the solution of
is the solution of
![]()
with![]() . Moreover1,
. Moreover1,![]() . ,
. ,
Remark 1. If (15) holds for![]() , then
, then![]() . Moreover, when
. Moreover, when![]() , (21) below holds and
, (21) below holds and ![]() is (also) left continuous, then both
is (also) left continuous, then both ![]() and
and ![]() is a continuous linear functional on
is a continuous linear functional on ![]() ((15) then holds for
((15) then holds for![]() ). ,
). ,
Remark 2. Let![]() , and let
, and let ![]() be the resolvent of the equation
be the resolvent of the equation
![]() (17)
(17)
![]() , so
, so![]() ,
, ![]() the identity map in
the identity map in![]() , and
, and![]() . Let
. Let![]() ,
, ![]() . For
. For![]() ,
, ![]() ,
, ![]() , is continuous in
, is continuous in ![]() -norm and hence can be represented
-norm and hence can be represented
by an ![]() -function
-function![]() ,
, ![]() progressively measurable and right continuous in t, a.s. and in
progressively measurable and right continuous in t, a.s. and in ![]() (even continuous in this manner if
(even continuous in this manner if ![]() is continuous). Note that if
is continuous). Note that if ![]() on
on ![]() then (16) implies
then (16) implies![]() .
.
Let ![]() be the natural filtration generated by the
be the natural filtration generated by the![]() ’s,
’s, ![]() augmented by the P-null sets in
augmented by the P-null sets in![]() . The function
. The function![]() , now taken to be a row vector, then satisfies the following condition: On
, now taken to be a row vector, then satisfies the following condition: On![]() , there exist
, there exist ![]() -valued, progressively measurable functions
-valued, progressively measurable functions![]() ,
, ![]() ,
, ![]() , all row
, all row
vectors, ![]() continuous in t, such that
continuous in t, such that![]() ,
, ![]() for all
for all![]() , and such that
, and such that
![]() (18)
(18)
and such that, for all![]() ,
, ![]() a.s.
a.s.
In this case, we have that for all![]() , for a.e. t, a.s.
, for a.e. t, a.s.
![]() (19)
(19)
When![]() ,
, ![]() is left continuous, and (21) below holds, the following additional properties hold:
is left continuous, and (21) below holds, the following additional properties hold:![]() ,
, ![]() , the
, the ![]() -limit (and a.s. limit)
-limit (and a.s. limit) ![]() exists,
exists, ![]() , and finally
, and finally
![]() (20)
(20)
Remark 3 The condition (15), with![]() , is implied by the following conditions:
, is implied by the following conditions: ![]() and for some
and for some![]() , for all
, for all![]() ,
,
![]() (21)
(21)
The ![]() -norm (or the norm
-norm (or the norm![]() ) used in the formulation of the condition (15) can have quite strong consequences. Assume for example that
) used in the formulation of the condition (15) can have quite strong consequences. Assume for example that![]() , and, for some
, and, for some![]() , that
, that ![]() for all
for all![]() . Then for some
. Then for some![]() ,
, ![]() for all
for all![]() , if
, if ![]() and
and ![]() (
(![]() and
and ![]() balls in
balls in ![]() -spaces,
-spaces,![]() ), but if U is strictly smaller than
), but if U is strictly smaller than ![]() it is neither possible to obtain this inclusion nor (15). When
it is neither possible to obtain this inclusion nor (15). When ![]() the situation may be different. Consider in particular the case where the original terminal constraint is, say
the situation may be different. Consider in particular the case where the original terminal constraint is, say![]() ,
,![]() . Using auxiliary controls
. Using auxiliary controls ![]() and auxiliary states z and y, the system can be rewritten as a system where the end constraints are
and auxiliary states z and y, the system can be rewritten as a system where the end constraints are![]() ,
, ![]() , by adding new state equations
, by adding new state equations![]() ,
, ![]() ,
, ![]() ,
, ![]() , and by changing the first
, and by changing the first ![]() state equations to read
state equations to read![]() ,
, ![]() ,
,![]() . Define
. Define![]() . We assume now
. We assume now![]() , so the control set in the rewritten system is now
, so the control set in the rewritten system is now![]() . The control
. The control ![]() is optimal in the rewritten system. Assume that
is optimal in the rewritten system. Assume that ![]() for some
for some ![]() for all
for all![]() . Then, for some
. Then, for some![]() , for all
, for all![]() ,
, ![]() , for
, for ![]() ,
, ![]() a ball in
a ball in![]() . Then for all
. Then for all![]() ,
, ![]() for all
for all ![]() so for all
so for all ![]() ,
,
![]() ,
,
![]() a ball in
a ball in![]() . Hence, for all
. Hence, for all![]() ,
, ![]() , where
, where ![]() (Necessary conditions for
(Necessary conditions for
systems with inequality constraints are stated in Remark 5 below, the local linear controllability condition just obtained suffices for the controllability condition in Remark 5 to apply to the original system).
3. Proof of Theorem 1
The proof consists of three lemmas and six proof steps A.-F., and relies on an “abstract” maximum principle, Corollary I in Appendix.
Without loss of generality, from now on let ![]() and let
and let![]() . Note that
. Note that![]() . For any
. For any![]() , let
, let ![]() be the solution of
be the solution of
![]() (22)
(22)
By general existence results and (1) and (2), ![]() , and
, and![]() , see (4), do exist, both unique, strong solutions, continuous in t (both column vectors).
, see (4), do exist, both unique, strong solutions, continuous in t (both column vectors).
A) Growth properties.
When![]() , by (1),
, by (1), ![]() and, similarly,
and, similarly,![]() . By (2), (4), and
. By (2), (4), and
(57) in Appendix, Lemma A, (a consequence of Gronwall’s inequality), with![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , we have, for some constant
, we have, for some constant ![]() independent of
independent of ![]() (only dependent on
(only dependent on![]() ), that
), that
![]() (23)
(23)
Let![]() . Using (2), and (57) in Appendix, Lemma A, (with
. Using (2), and (57) in Appendix, Lemma A, (with![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , for some constant D independent of
, for some constant D independent of ![]() and u (only dependent on
and u (only dependent on![]() ), we get
), we get
![]() (24)
(24)
(the last inequality by (2)).
Let![]() . As explained below, for some
. As explained below, for some![]() , we have
, we have
![]() (25)
(25)
The inequality (25) follows from (57) in Appendix, Lemma A, together with (2), for![]() ,
, ![]() ,
, ![]() ,
, ![]() (
(![]() ), and
), and
![]()
![]()
Similarly2, for![]() ,
,
![]() (26)
(26)
In (25) and (26), ![]() is independent of
is independent of ![]() (it only depends on
(it only depends on![]() ).
).
We need to prove that
![]() (27)
(27)
This follows from (24) and (2), because, in a shorthand notation, for all t,
![]()
We also need:
![]() (28)
(28)
This follows from (26) and (2), because, in a shorthand notation, for![]() ,
, ![]() , for all t,
, for all t,
![]()
Note finally that, when![]() ,
, ![]() , then
, then
![]() (29)
(29)
see Remark L in Appendix.
B) Local controllability of the linear perturbations.
Note that, by (2), in a shorthand notation,
![]() (30)
(30)
when![]() ,
,![]() . Then, from (15) and (29), when
. Then, from (15) and (29), when![]() ,
,
![]() (31)
(31)
where “co” can be omitted due to the concavity of U. To see this, apply Remark W in Appendix.
Next, let the number ![]() satisfy
satisfy![]() , (for
, (for![]() , see (25)), and let
, see (25)), and let ![]() . Let
. Let ![]() , so
, so![]() . When
. When ![]() , then
, then![]() , hence
, hence![]() . Then, for all
. Then, for all![]() , for all t
, for all t
![]() (32)
(32)
To see this, note that by (25), for all t,
![]()
![]()
Then, using again Remark W in Appendix and (31), (29), (32), for all![]() ,
,
![]() (33)
(33)
C) Relations between exact and linear perturbations.
Let ![]() be given elements in
be given elements in![]() . Let
. Let ![]() be arbitrarily given. Let us first prove that for
be arbitrarily given. Let us first prove that for ![]() small enough, for any
small enough, for any![]() , for
, for![]() , for all t,
, for all t,
![]() (34)
(34)
Write![]() ,
,![]() . Define, in a shorthand notation,
. Define, in a shorthand notation,
![]()
![]()
![]()
![]()
For any![]() , there exists a
, there exists a![]() , such that
, such that
![]() (35)
(35)
by Lemmas B and C in Appendix.
Consider now
![]()
By (56) in Appendix, Lemma A, for![]() , for some
, for some ![]() only dependent on
only dependent on![]() , for all t
, for all t
![]() (36)
(36)
To see this, in Lemma A let![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . To obtain (34), put
. To obtain (34), put![]() .
.
Next, given ![]() and assume that
and assume that ![]() Let us prove that for any
Let us prove that for any![]() , for
, for ![]() small enough, for any
small enough, for any![]() , for
, for![]() , we have that
, we have that
![]() (37)
(37)
Let
![]()
Now,
![]()
Because ![]() and
and![]() , then Lemma J in Appendix gives that
, then Lemma J in Appendix gives that ![]() when
when![]() . Next, let
. Next, let![]() ,
,![]() . Using
. Using ![]() and
and![]() , we get
, we get![]() , which
, which ![]() when
when![]() , by (36). Hence, (37) follows.
, by (36). Hence, (37) follows.
D) Continuity of ![]() at
at![]() .
.
Let![]() . Define
. Define![]() . Let us first prove that
. Let us first prove that
![]() (38)
(38)
Now, in a shorthand notation,
![]()
![]()
![]()
Using the notation in Lemma A in Appendix, we write ![]() where
where ![]() ,
, ![]() ,
,
![]()
![]()
(![]() ,
,![]() ,
,![]() ).
).
Then, by (57),
![]()
where
![]()
for
![]()
and
![]()
for
![]()
Consider e.g the term ![]() . Now,
. Now, ![]() ,
, ![]() , and
, and ![]() when
when ![]() , Hence, by Remark T in Appendix,
, Hence, by Remark T in Appendix, ![]() when
when![]() . Similarly, the terms containing
. Similarly, the terms containing ![]() converge to zero when
converge to zero when![]() . So
. So ![]() uniformly in t when
uniformly in t when![]() .
.
Next, assume that![]() ,
,![]() . We want to prove that then
. We want to prove that then ![]() satisfies
satisfies
![]() (39)
(39)
where, in a shorthand notation,
![]()
Now,
![]()
Let us show that the four terms in square brackets have ![]() -norms
-norms ![]() when
when![]() . Now,
. Now, ![]() when
when![]() . Hence, by Lemma J in Appendix, the second and fourth square bracket
. Hence, by Lemma J in Appendix, the second and fourth square bracket ![]() in
in ![]() when
when ![]() (recall that
(recall that ![]() and
and![]() ). Moreover the first and third square bracket have
). Moreover the first and third square bracket have ![]() -norms smaller than
-norms smaller than ![]() and
and![]() , respectively. So the
, respectively. So the ![]() -norms of both these terms
-norms of both these terms ![]() when
when![]() , recall that
, recall that ![]() when
when![]() , see (38). So (39) has been proved.
, see (38). So (39) has been proved.
E) Dense subsets of![]() .
.
Let ![]() (for this equality see Appendix L). Note that for each
(for this equality see Appendix L). Note that for each![]() , for some
, for some![]() ,
,![]() . Let
. Let![]() . For each
. For each![]() , let
, let ![]() be the projection of
be the projection of ![]() on the line containing 0 and
on the line containing 0 and![]() . Let
. Let ![]() if
if ![]() has the opposite direction of
has the opposite direction of ![]() or if
or if![]() , let
, let ![]() if
if ![]() is longer than
is longer than ![]() and has the same direction as
and has the same direction as![]() , and if
, and if ![]() is smaller than
is smaller than ![]() and has the same direction as
and has the same direction as![]() , let
, let![]() . Evidently, for some measurable
. Evidently, for some measurable![]() ,
, ![]() , and
, and ![]() and
and ![]() (
(![]() also depends on
also depends on![]() , the notation hides this fact). Evidently,
, the notation hides this fact). Evidently, ![]() and
and ![]() is progressively measurable. Now, for any
is progressively measurable. Now, for any![]() , let
, let ![]() . We have that
. We have that ![]() is
is ![]() -dense in
-dense in ![]() because if
because if![]() , for any
, for any![]() , for some
, for some![]() ,
, ![]() (
(![]() , and hence,
, and hence, ![]() , belong
, belong
to the linear space![]() ). Then
). Then ![]() , and so
, and so ![]() for
for ![]() (
(![]() is convex).
is convex).
Note finally that if![]() , then
, then![]() ,
, ![]() for
for![]() , so
, so![]() , in fact
, in fact
![]() (40)
(40)
F) Final proof steps.
Define
![]() (41)
(41)
Using Jensens inequality, for an arbitrary function ![]() we get
we get![]() . It follows that
. It follows that
![]() (42)
(42)
For![]() , define
, define ![]() and
and ![]() . Define
. Define
![]()
![]() (43)
(43)
Furthermore, let ![]() be the subset of
be the subset of ![]() consisting of all element
consisting of all element ![]() such that
such that ![]() and such that
and such that![]() , (limit in
, (limit in ![]() -norm,
-norm,![]() ). It is easily seen that elements of the type
). It is easily seen that elements of the type![]() ,
, ![]() ,
, ![]() , precisely make up the
, precisely make up the
set![]() . To see this, let
. To see this, let ![]() be such a function, and, using Jensen’s inequality three times (and for any
be such a function, and, using Jensen’s inequality three times (and for any![]() , that
, that ![]() ), note that for any interval
), note that for any interval![]() ,
,
![]() (44)
(44)
so, in particular,![]() . This yields also, for
. This yields also, for![]() , that
, that
![]() (45)
(45)
so![]() , see (43). Moreover, by (44), similarly,
, see (43). Moreover, by (44), similarly,
![]() (46)
(46)
so ![]() is a
is a ![]() -limit of
-limit of![]() . Hence,
. Hence, ![]() . Note also that
. Note also that ![]()
![]()
![]()
for all ![]() (holding “the more” for
(holding “the more” for![]() ).
).
Finally, if![]() , then
, then![]() , for
, for
![]() (47)
(47)
where![]() ,
,
and where![]() ,
, ![]() progressively measurable. (So the linear map
progressively measurable. (So the linear map ![]() satisfies
satisfies![]() .)
.)
Let ![]() be the linear map from
be the linear map from ![]() (see (43)) into
(see (43)) into ![]() defined by
defined by ![]() and note that
and note that![]() ,
,![]() . In (45) we have just proved that
. In (45) we have just proved that ![]() has norm
has norm ![]() for the norms
for the norms ![]() and
and ![]() (or for
(or for![]() , as we shall express it).
, as we shall express it).
Now, let![]() , let cl(2) be closure in
, let cl(2) be closure in ![]() in
in ![]() -norm, let
-norm, let![]() , let
, let ![]() , and let
, and let ![]() be a
be a ![]() -ball in
-ball in ![]() .
.
Now, for![]() , we have
, we have![]() , where
, where
![]() (48)
(48)
Hence, by (33), using ![]() and
and![]() , for
, for![]() , (for
, (for ![]() and
and![]() , used in a moment, see definitions subsequent to (31)), we get
, used in a moment, see definitions subsequent to (31)), we get
![]()
where
![]() (49)
(49)
(note that ![]() is continuous in
is continuous in![]() , as shown above). Let
, as shown above). Let![]() ,
,![]() . Then
. Then
![]()
Using Remark W, ![]() , and the fact that the first integrand has a
, and the fact that the first integrand has a ![]() -norm
-norm ![]() by (32) (hence the first integral has a
by (32) (hence the first integral has a ![]() -norm
-norm![]() , we get from (49) that
, we get from (49) that
![]() (50)
(50)
Observe that, given![]() ,
, ![]() (
(![]() ), by
), by ![]() for
for ![]() and (37), for any given
and (37), for any given![]() , for
, for ![]() small enough, for any
small enough, for any![]() ,
,
![]() (51)
(51)
And, by (39) and![]() , for
, for ![]() (
(![]() ), then
), then
![]() (52)
(52)
To obtain the conclusion in Theorem 1, we will now apply Corollary I in Appendix, and for this end, we make the following identifications:![]() ,
, ![]() (for
(for ![]() see below),
see below), ![]() ,
, ![]() ,
, ![]() , the norm
, the norm ![]() on
on ![]() equal to
equal to![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() . By (34) and (51) it follows that the property (61) is satisfied for
. By (34) and (51) it follows that the property (61) is satisfied for ![]() for
for ![]() (
(![]() by (40)), and (62) is trivially satisfied by concavity of U, both (61) and (62) in the manner required in Corollary I. By (50), for
by (40)), and (62) is trivially satisfied by concavity of U, both (61) and (62) in the manner required in Corollary I. By (50), for![]() ,
, ![]() for
for![]() , so for
, so for![]() ,
, ![]() ,
,![]() ), where
), where![]() ,
, ![]() defined subsequent to (31). By
defined subsequent to (31). By ![]() and (27) and (24),
and (27) and (24), ![]() and
and ![]() are continuous. By (26), (28), and
are continuous. By (26), (28), and![]() ,
, ![]() is continuous in
is continuous in![]() , for any
, for any![]() , and by (38) and (52), for
, and by (38) and (52), for![]() ,
, ![]() is continuous at
is continuous at![]() . The required boundedness of
. The required boundedness of ![]() is satisfied because of (25). Evidently,
is satisfied because of (25). Evidently, ![]() is complete, see Appendix, Remark M. Hence all conditions in Corollary I are satisfied. Thus, for some
is complete, see Appendix, Remark M. Hence all conditions in Corollary I are satisfied. Thus, for some![]() , some
, some ![]() -continuous linear functional
-continuous linear functional ![]() on
on![]() ,
, ![]() , for all
, for all![]() ,
, ![]() .
.
By Hahn-Banach’s theorem, ![]() has an
has an ![]() -continuous linear extension to all
-continuous linear extension to all![]() , also denoted
, also denoted![]() .
.
Proof of Remark 1. Let![]() . Note that (50) and
. Note that (50) and ![]() gives
gives![]() . If
. If![]() , the necessary condition
, the necessary condition
(16) implies ![]() and hence
and hence ![]() , a contradiction. So
, a contradiction. So![]() .
.
From (16), in a shorthand notation, we get, for![]() , and even for
, and even for![]() , that
, that
![]() (53)
(53)
Fix any![]() , such that
, such that ![]() By (21) and
By (21) and![]() , there exists a
, there exists a![]() , such that
, such that ![]() ,
, ![]() . So
. So ![]() , where
, where![]() ,
, ![]() , so
, so ![]() (
(![]() ) and
) and![]() .
.
By (25), for some constant K, ![]() , so the absolute value of the scalar products on the right hand side of (53) are smaller than
, so the absolute value of the scalar products on the right hand side of (53) are smaller than ![]() (
(![]() ,
,![]() ) and
) and
![]() , respectively, the last number being small than
, respectively, the last number being small than ![]() . Hence, by (53), for
. Hence, by (53), for ![]() ,
,![]() . Replacing
. Replacing ![]() by
by![]() , by the same argument, if
, by the same argument, if![]() , we get
, we get![]() . In fact, we have
. In fact, we have ![]() for all
for all![]() ,
,![]() .
.
Thus, on this subspace of![]() ,
, ![]() is
is ![]() -continuous. Hence, by Hahn-Banach’s theorem (see [8] ) and a representation theorem, for some
-continuous. Hence, by Hahn-Banach’s theorem (see [8] ) and a representation theorem, for some ![]() in
in![]() ,
, ![]() , for all
, for all ![]() (in fact on
(in fact on ![]() ).
).
Note that for![]() ,
, ![]() , which
, which
means that ![]() is
is ![]() -continuous on
-continuous on ![]() and has a unique
and has a unique ![]() -continuous extension to the
-continuous extension to the ![]() -closure of
-closure of![]() , which equals
, which equals ![]() (and includes
(and includes![]() ) in case of left continuity of
) in case of left continuity of![]() .
.
Proof of Remark 2.
Let![]() ,
,![]() . Let
. Let ![]() (
(![]() ) and let
) and let ![]() and
and ![]() be the adjoints of
be the adjoints of ![]() and of
and of![]() .
.
It is easily proved (using Lemma A in Appendix and ![]() for
for![]() ) that for
) that for![]() ,
, ![]() for some constant D, see Remark P in Appendix. Hence, for any given
for some constant D, see Remark P in Appendix. Hence, for any given![]() , by the
, by the ![]() -continuity of
-continuity of ![]() on
on![]() ,
, ![]() and hence of
and hence of![]() , there exists a
, there exists a ![]() -function
-function ![]() on
on ![]() such that for any
such that for any ![]() -function
-function![]() , we have
, we have![]() . The function
. The function ![]() is progressively measurable and right continuous in
is progressively measurable and right continuous in![]() , both a.s. and in
, both a.s. and in![]() , see arguments in Remark Q in Appendix.
, see arguments in Remark Q in Appendix.
Assume now![]() , (21) and left continuity of
, (21) and left continuity of![]() , which implies
, which implies ![]() -continuity of
-continuity of ![]() on all
on all ![]() (by extension). In this case the argument for
(by extension). In this case the argument for ![]() -continuity of
-continuity of ![]() for
for ![]() in Remark Q in Appendix extends to
in Remark Q in Appendix extends to![]() . Let
. Let ![]() be a representation of
be a representation of ![]() and let
and let![]() . Consider now
. Consider now
![]()
where![]() . In this case, we can evidently put
. In this case, we can evidently put ![]() and we have
and we have
![]()
In case of![]() , (21), and left continuity of
, (21), and left continuity of![]() , by
, by ![]() -continuity of
-continuity of![]() , the two definitions of
, the two definitions of ![]() coincide, because for both definitions we have
coincide, because for both definitions we have ![]() for all
for all ![]() , t arbitrary in
, t arbitrary in![]() .
.
Let now ![]() be the natural filtration generated by the
be the natural filtration generated by the![]() ’s , augmented by the P-null sets in
’s , augmented by the P-null sets in![]() , and let
, and let![]() .
.
Then, consider the pair of equations
![]() (54)
(54)
![]() (55)
(55)
By Theorem 2.2, p. 349 in [6] , there is a unique progressively measurable collection ![]()
![]() ,
, ![]() continuous in
continuous in![]() , satisfying these equations (or more precisely, a.s. the integrated version of these equations),
, satisfying these equations (or more precisely, a.s. the integrated version of these equations), ![]() ,
, ![]() , with
, with ![]() equal to
equal to ![]() -a.s. for each t (see Remark O in Appendix). The uniqueness says that if two pairs
-a.s. for each t (see Remark O in Appendix). The uniqueness says that if two pairs![]() , (
, (![]() ) and
) and ![]() satisfy the pair of equations, then
satisfy the pair of equations, then ![]() for all
for all ![]() and
and ![]() for a.e.
for a.e.![]() . We can let
. We can let ![]() when
when ![]() (
(![]() ) and obtain such functions
) and obtain such functions ![]() defined on each
defined on each![]() . For
. For![]() , by the fact that
, by the fact that ![]() a.s. and uniqueness, we have that
a.s. and uniqueness, we have that ![]() for a.e
for a.e ![]() a.s. Then, evidently, there exists a unique pair
a.s. Then, evidently, there exists a unique pair ![]() on
on ![]() satisfying (54), with
satisfying (54), with ![]() a.s. equal to
a.s. equal to ![]() for any
for any![]() ,
, ![]() ,
, ![]() for all
for all![]() ,
, ![]() continuous.
continuous.
Let us show (19). For any![]() ,
, ![]() if
if ![]() on
on![]() , so in this case
, so in this case ![]() (a consequence of (16)).
(a consequence of (16)).
Define ![]() and
and![]() ,
, ![]() , and
, and ![]() similarly. It turns out that
similarly. It turns out that
![]() . From this and
. From this and ![]() it follows that for all
it follows that for all![]() ,
, ![]() for a.e.
for a.e.![]() , a.s., see Remark S. In fact, this holds for a.e.
, a.s., see Remark S. In fact, this holds for a.e. ![]() because
because ![]() was arbitrary. An informal proof, using Ito’s formula, shows the last equality:
was arbitrary. An informal proof, using Ito’s formula, shows the last equality:
![]()
So
![]()
Remark 4. (Exact attainability). In Theorem 1, drop the assumption that ![]() is optimal (and the optimization problem), so (
is optimal (and the optimization problem), so (![]() ) is simply a pair satisfying
) is simply a pair satisfying
(4) and ![]() a.s. Then, for each
a.s. Then, for each![]() ,
, ![]() , (cl2 and int = interior both corresponding to
, (cl2 and int = interior both corresponding to ![]()
and the space![]() ), for all
), for all![]() , for some number
, for some number ![]() and some control
and some control![]() ,
, ![]() a.s. ,
a.s. ,
Proof of Remark 4. Let![]() ,
,![]() . Corollary G in Appendix will be applied. Let
. Corollary G in Appendix will be applied. Let![]() ,
, ![]() ,
, ![]() , the norm
, the norm ![]() on Y equal to
on Y equal to![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() . Recall that
. Recall that![]() ,
, ![]() when
when![]() . By (51) it follows that the property (61) is satisfied for
. By (51) it follows that the property (61) is satisfied for ![]() for
for![]() , and (62) is trivially satisfied. By (27) H is continuous, by (28),
, and (62) is trivially satisfied. By (27) H is continuous, by (28), ![]() is continuous in A for any
is continuous in A for any![]() , and by (52), for
, and by (52), for![]() ,
, ![]() is continuous at
is continuous at![]() .
.
Assume that ![]() and let
and let![]() . For any
. For any![]() , it was shown earlier that there exists a
, it was shown earlier that there exists a ![]() such that
such that![]() ,
, ![]() (
(![]() ,
, ![]() ,
,![]() ), so
), so ![]() and
and![]() . Thus, if
. Thus, if ![]() , then
, then ![]() . Hence all conditions in Corollary G are satisfied and the conclusion in Remark 4 follows. ,
. Hence all conditions in Corollary G are satisfied and the conclusion in Remark 4 follows. ,
Remark 5 If it is required that ![]() instead of
instead of![]() , where C is a
, where C is a ![]() -closed convex set in
-closed convex set in![]() , and if (15) holds for
, and if (15) holds for ![]() replaced by
replaced by
![]() ,
, ![]() (for
(for ![]() see (47)), then
see (47)), then
(16) again holds, and with![]() . In particular, this holds if
. In particular, this holds if ![]() a.s,
a.s, ![]() ,
, ![]() a.s.,
a.s., ![]() ,
, ![]() given numbers. In fact, because
given numbers. In fact, because ![]() automatically, the results here cover the case where the terminal constraints are
automatically, the results here cover the case where the terminal constraints are ![]() a.s,
a.s, ![]() ,
, ![]() a.s.,
a.s.,![]() . ,
. ,
Proof of Remark 5. A proof can be obtained (for![]() ) by replacing
) by replacing ![]() by
by ![]() and
and ![]() by
by![]() , with
, with ![]() replaced by
replaced by![]() , and
, and ![]() replaced by
replaced by![]() , keeping
, keeping ![]() and
and ![]() as before and letting
as before and letting![]() ,
,![]() . (Then
. (Then![]() ,
, ![]() ,
, ![]() ,
, ![]() , gives
, gives ![]() , i.e.
, i.e. ![]() ). The details are omitted.
). The details are omitted.
Remark 6 (The case ![]() for some or all j,
for some or all j,![]() ). Let
). Let ![]() be closure in
be closure in ![]() as well as in
as well as in![]() . For
. For![]() , let
, let
![]() . When
. When![]() , and
, and ![]() is the
is the
natural filtration, augmented by null sets as before, the necessary condition of Theorem 1 can be obtained for ![]() defined and continuous on
defined and continuous on ![]() (with
(with![]() ,
,![]() ), if, for some
), if, for some![]() , for some
, for some![]() , for some
, for some![]() ,
,
a) for some![]() ,
, ![]() ,
, ![]() when
when![]() ,
, ![]() , where
, where
![]()
If![]() , then
, then![]() . The condition (A), with
. The condition (A), with![]() , is implied by
, is implied by
b): For some![]() , for all
, for all![]() , for any
, for any![]() ,
,
![]()
Letting![]() ,
, ![]() , and
, and ![]() , it is here sufficient to operate with the
, it is here sufficient to operate with the ![]()
-norm instead of ![]() on
on![]() , with
, with![]() . Note that
. Note that![]() , so (A) holds for
, so (A) holds for ![]() replaced by
replaced by![]() . The set arising by replacing
. The set arising by replacing ![]() by
by ![]() in
in ![]() is
is
denoted![]() . Define
. Define![]() . The condition (A), so modified, implies that for some
. The condition (A), so modified, implies that for some![]() ,
, ![]() ,
,
![]() close to
close to ![]() a ball in
a ball in![]() , so
, so ![]() (
(![]() close to
close to![]() ). See Appendix, Remark V for the next to last inclusion and the implication (B) Þ (A).
). See Appendix, Remark V for the next to last inclusion and the implication (B) Þ (A).
Now, in the manner required in Corollary I, (34) Þ (61) (with![]() ,
, ![]() ,
,![]() ), (24) and (26) implies continuity of
), (24) and (26) implies continuity of ![]() and
and![]() , and (38) implies continuity of
, and (38) implies continuity of ![]() at
at![]() .
.
4. Conclusion
In this paper, necessary conditions for optimal control of diffusions with hard end restrictions on the states have been obtained. The main case considered is the one where the states restricted at the terminal time correspond to differential equations not containing Brownian motions. Brownian motions only occur in differential equations for states unconstrained at the terminal time. A removal of this restriction is discussed in Remark 6.
Acknowledgements
The author is grateful to a referee for useful comments.
Appendix
The appendix contains, among other things, a number of wellknown results, included for the convenience of the reader. The first one concerns a result on comparison of solutions. Still![]() .
.
Lemma A. Assume that ![]() (an
(an ![]() -vector) and
-vector) and![]() , (a
, (a ![]() matrix, with columns
matrix, with columns![]() ,
,![]() ) are Lipschitz continuous in
) are Lipschitz continuous in ![]() with rank
with rank ![]() and progressively measurable in
and progressively measurable in![]() . Assume that six progressively measurable functions
. Assume that six progressively measurable functions ![]() and
and ![]() exist (
exist (![]() ,
,![]()
![]() -matrices), satisfying
-matrices), satisfying
![]()
and
![]()
where![]() . We assume that the eight integrands belong to
. We assume that the eight integrands belong to ![]() -spaces. Then, for some constant
-spaces. Then, for some constant![]() ,
,
![]() (56)
(56)
(applied to matrices the index j indicates columns), and for some constant![]() ,
,
![]() (57)
(57)
![]() and
and ![]() only dependent on
only dependent on![]() .
.
Proof of (57). We shall use a shorthand notation. Using the algebraic inequality![]() , then for some positive constant k,
, then for some positive constant k,
![]()
![]()
The Burkholder-Davis-Gundy inequality yields, for a “universal” constant
![]() , that
, that![]() .
.
Similar inequalities hold for the other terms involving![]() . Hence (using also Jensen’s inequality) we get
. Hence (using also Jensen’s inequality) we get
![]()
![]()
![]()
![]()
Note that, by Gronwall’s inequality, for any functions![]() ,
, ![]() , if
, if ![]() , and
, and ![]() is increasing, then
is increasing, then![]() . Hence, for
. Hence, for![]() ,
,
![]()
Using the fact that the square root of a sum of positive numbers is £ the sum of square roots of the numbers, we get
![]()
Note that![]() , and that
, and that ![]() . Using this for the term containing
. Using this for the term containing![]() , and a similar argument for the term containing
, and a similar argument for the term containing![]() , then (57) follows.
, then (57) follows.
Proof of (56).
Using Ito’s isometry,
![]()
![]()
![]()
Then, again using ![]() and Jensen’s inequality, for some positive constant k,
and Jensen’s inequality, for some positive constant k,
![]()
![]()
![]()
![]()
Thus, for![]() ,
,
![]()
so (56) follows.
Simple results om Gâteaux derivatives appear in the next two lemmas.
Lemma B. Let ![]() be continuously differentiable in z for each t, and have one-sided limits with respect to t, and assume
be continuously differentiable in z for each t, and have one-sided limits with respect to t, and assume ![]() for all
for all![]() . For each
. For each![]() , for each “direction”
, for each “direction”![]() , and for each t,
, and for each t, ![]() (
(![]() ), has, in the norm
), has, in the norm![]() , a bounded linear Gâteaux derivative at
, a bounded linear Gâteaux derivative at ![]() in direction
in direction![]() , which equals
, which equals
![]() . The derivative is uniform in t.
. The derivative is uniform in t.
Proof. By Ito’s isometry,
![]()
When![]() , the term in curly brackets converges to zero for each
, the term in curly brackets converges to zero for each ![]() and is smaller than the
and is smaller than the ![]() -function
-function![]() . Hence, Lebesgue’s dominated convergence theorem gives that
. Hence, Lebesgue’s dominated convergence theorem gives that ![]() when
when![]() . ,
. ,
Lemma C. Let ![]() be continuously differentiable in z for each t, and have one-sided limits with respect to t, and assume
be continuously differentiable in z for each t, and have one-sided limits with respect to t, and assume ![]() for all
for all![]() . For each
. For each![]() , for each “direction”
, for each “direction” ![]() , and for each t,
, and for each t, ![]() (
(![]() ), has, in the norm
), has, in the norm![]() , a bounded linear Gâteaux derivative at
, a bounded linear Gâteaux derivative at ![]() in direction
in direction![]() , which in equals
, which in equals ![]() . The derivative is uniform in t.
. The derivative is uniform in t.
Proof. Define
![]()
![]()
Jensen’s inequality yields the inequality![]() . The remaining arguments are as in the preceding proof, they yield
. The remaining arguments are as in the preceding proof, they yield ![]() when
when![]() . ,
. ,
Below, on product spaces, maximum norms (= maximum of norms) and maximum metrics are used. In the sequel, the following entities are used:
Y is a normed space, A is a complete pseudometric space with pseudo-metric r, and a* is a given element in A. The function H(a) from A into Y is continuous. (58)
Theorem D. (Attainability) Let the entities in (58) be given. Let positive numbers![]() , and an element
, and an element ![]() in Y be given. Assume that the following properties hold for all
in Y be given. Assume that the following properties hold for all![]() : For all
: For all ![]() with
with![]() , for all
, for all![]() , a pair
, a pair ![]() exists, such that
exists, such that
![]() and
and![]() . (59)
. (59)
Then, for all![]() , there exists a pair
, there exists a pair![]() , such that
, such that![]() , where
, where![]() .
.
Corollary E. Assume that![]() . Then, in (59), evidently
. Then, in (59), evidently ![]() can be replaced by the stronger inequality
can be replaced by the stronger inequality![]() . ,
. ,
(On the other hand, when![]() , then
, then ![]() Þ
Þ ![]() for
for![]() .)
.)
Central ideas in the proof of Theorem D stem from the proof of the multifunction inverse function theorem Theorem 4, p. 431, in [9] .
Proof of Theorem D. The property (59) also holds for ![]() in the set
in the set![]() . To see this, let
. To see this, let ![]() and let
and let![]() . Then
. Then ![]() for some
for some![]() , some
, some ![]() such that
such that![]() . Now, for all
. Now, for all![]() , there exists a pair
, there exists a pair![]() ,
, ![]() , such that the inequalities in (59) hold. From these inequalities, for
, such that the inequalities in (59) hold. From these inequalities, for![]() , using
, using![]() , it follows that
, it follows that ![]() and
and ![]() . Hence, (59) holds for
. Hence, (59) holds for![]() .
.
Below, write![]() . The following lemma is needed in the proof:
. The following lemma is needed in the proof:
Lemma F. Let![]() . Assume that the pair
. Assume that the pair ![]() minimizes
minimizes
![]()
in![]() . Then
. Then![]() .
.
Proof of Lemma F. By contradiction, assume![]() ,
,![]() . The vector
. The vector ![]() satisfies
satisfies![]() , so
, so ![]() belongs to
belongs to![]() . Hence, by the extended property (59), there exist an
. Hence, by the extended property (59), there exist an ![]() and a
and a![]() ,
, ![]() , such that
, such that
![]() (60)
(60)
Moreover, ![]() , (use the first inequality for
, (use the first inequality for![]() ), which implies
), which implies ![]() Define
Define ![]()
![]() . Then, using (60),
. Then, using (60), ![]() , and the definition of
, and the definition of![]() , we get
, we get
![]()
Using ![]() and
and ![]() yields
yields
![]()
a contradiction of the optimality of![]() .
.
Continued proof of the theorem. Let![]() ,
,
let ![]() be as in the conclusion of the theorem, and let
be as in the conclusion of the theorem, and let ![]() . Note that
. Note that![]() . Let the distance between
. Let the distance between ![]() and
and ![]() be
be ![]() in the complete space
in the complete space ![]() . By Aubin and Ekeland (1984, Theorem 1, p. 255), (Ekeland’s variational principle), there exists a
. By Aubin and Ekeland (1984, Theorem 1, p. 255), (Ekeland’s variational principle), there exists a ![]() such that
such that
![]()
for all ![]() and
and
![]()
which gives![]() ,
,![]() . By Lemma F,
. By Lemma F, ![]() , so
, so![]() , for
, for![]() . ,
. ,
Below, ![]() is a sort of Gâteaux derivative at a of
is a sort of Gâteaux derivative at a of![]() .
.
Corollary G. Let![]() , Y a normed space, A a complete pseudometric space with metric
, Y a normed space, A a complete pseudometric space with metric![]() ,
, ![]() a given element in A, and let
a given element in A, and let ![]() be continuous. For each
be continuous. For each![]() , let
, let ![]() be a set dense in A. Assume the existence of a function
be a set dense in A. Assume the existence of a function![]() , from
, from ![]() into Y and a positive constant
into Y and a positive constant ![]() such that, for each
such that, for each![]() , for all
, for all![]() , all
, all![]() , all
, all![]() , there exists a pair
, there exists a pair![]() ,
, ![]() ,
, ![]() such that
such that
![]() (61)
(61)
Assume also that for all![]() ,
,
![]() (62)
(62)
Assume that ![]() is continuous in A for any
is continuous in A for any![]() , and that
, and that ![]() is continuous at
is continuous at ![]() for any
for any![]() . Assume finally that b is an interior point in
. Assume finally that b is an interior point in![]() , and that, for some
, and that, for some![]() , some
, some![]() ,
, ![]() for all
for all![]() . Then, for some
. Then, for some ![]() and some
and some![]() ,
, ![]() .
.
Proof. Write![]() , and let
, and let ![]() for some
for some![]() . Then, for some
. Then, for some![]() ,
,![]() . Define
. Define![]() . Evidently, b is an interior point in
. Evidently, b is an interior point in ![]() if
if![]() . Then b is an interior point in
. Then b is an interior point in ![]() even if
even if ![]() is only an approximate equality, in fact there exist positive numbers
is only an approximate equality, in fact there exist positive numbers ![]() and
and ![]() such that
such that ![]() for all
for all![]() . Because
. Because![]() , by (62) there exists a
, by (62) there exists a![]() , such that
, such that![]() , and we can even assume
, and we can even assume![]() , by density of
, by density of ![]() and continuity of
and continuity of![]() . By the continuity of
. By the continuity of ![]() in the corollary, for
in the corollary, for ![]() small enough,
small enough, ![]() for
for![]() . We assume
. We assume![]() ,
,![]() . Evidently,
. Evidently,![]() . Hence,
. Hence, ![]() for all
for all![]() . Thus, for
. Thus, for![]() ,
, ![]() , because
, because ![]() and
and ![]() is convex. Hence,
is convex. Hence, ![]() ,
,![]() . It follows that if
. It follows that if![]() ,
,![]() , then, for any
, then, for any![]() , by (62), for some
, by (62), for some![]() ,
, ![]() ,
,
![]() (63)
(63)
We can even assume ![]() by continuity of
by continuity of![]() . By (61), for
. By (61), for![]() , for some
, for some![]() , and some arbitrarily small
, and some arbitrarily small![]() ,
,
![]() (64)
(64)
Now, by (63),![]() . Then, by (64),
. Then, by (64),
![]() (65)
(65)
(![]() ,
, ![]() ,
,![]() ). In Theorem D, replace
). In Theorem D, replace ![]() by
by![]() , a by
, a by![]() ,
, ![]() by
by ![]() and A by
and A by![]() , and let
, and let![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Then the conditions in Theorem D are satisfied when, in (59),
. Then the conditions in Theorem D are satisfied when, in (59), ![]() is replaced by
is replaced by![]() ,
, ![]() as just constructed,
as just constructed, ![]() , (
, (![]() , for
, for![]() ,
, ![]() , and
, and ![]() as
as ![]() ). Thus, we get that, for all
). Thus, we get that, for all ![]() small enough,
small enough, ![]() for some
for some![]() , or
, or ![]() .
.
Remark H. If![]() , then
, then ![]() can be taken to be arbitrary small (b can be replaced by
can be taken to be arbitrary small (b can be replaced by ![]() for any
for any![]() ). Hence, in this case,
). Hence, in this case, ![]() holds for some arbitrarily small
holds for some arbitrarily small![]() .
.
Corollary I Let ![]() be a normed space, let
be a normed space, let![]() , let
, let ![]() be a complete pseudometric space with metric
be a complete pseudometric space with metric ![]() and let
and let ![]() be dense in
be dense in![]() . Assume that
. Assume that ![]() is a given element in
is a given element in![]() , let
, let ![]() be continuous. Let
be continuous. Let![]() ,
,![]() . Assume that (61) and (62) are satisfies for
. Assume that (61) and (62) are satisfies for ![]() replaced by
replaced by ![]() and also that
and also that ![]() is continuous at
is continuous at ![]() for any
for any ![]() and that
and that ![]() is continuous for any
is continuous for any![]() , with
, with ![]() for all
for all![]() . Assume, for some given
. Assume, for some given![]() , that
, that ![]() . Assume also, for some
. Assume also, for some![]() , some
, some![]() , that
, that ![]() for all
for all![]() . Assume, finally, that
. Assume, finally, that![]() . Then, for some nonzero continuous linear functional
. Then, for some nonzero continuous linear functional ![]() on
on![]() ,
, ![]() a number
a number![]() , we have
, we have ![]() for all
for all![]() .
.
Proof. Define![]() , and
, and![]() . Define
. Define ![]() . Evidently, for
. Evidently, for ![]() ,
, ![]() and
and ![]() , so
, so![]() . Assume by contradiction that
. Assume by contradiction that ![]() belongs to
belongs to ![]() for some
for some![]() . Define
. Define![]() , and for
, and for![]() ,
, ![]() , let
, let ![]() ,
, ![]() and
and ![]() , and let
, and let![]() ,
,![]() . Then, for
. Then, for![]() ,
, ![]() (62) and (61) are evidently satisfied, (the latter for
(62) and (61) are evidently satisfied, (the latter for ![]() when
when![]() ). Obviously,
). Obviously, ![]() for each
for each ![]() where
where ![]() (Þ
(Þ![]() Þ
Þ![]() Þ
Þ![]() ). Hence, by the preceding corollary, for some
). Hence, by the preceding corollary, for some![]() ,
, ![]() for some
for some![]() . Hence,
. Hence, ![]() ,
, ![]() , or
, or![]() , contradicting optimality. Thus the set
, contradicting optimality. Thus the set ![]() is disjoint from
is disjoint from![]() , so the convex set L can be separated from the convex set int
, so the convex set L can be separated from the convex set int![]() by a nonzero continuous linear functional
by a nonzero continuous linear functional ![]() such that
such that![]() ,
, ![]() , which implies
, which implies![]() .
.
Lemma J. Let![]() . Let
. Let ![]() be continuous in z and measurable in t. Assume that
be continuous in z and measurable in t. Assume that ![]() exists for all
exists for all ![]() and that
and that ![]() for all
for all![]() . Let
. Let ![]() be continuous in
be continuous in ![]() at
at![]() , uniformly in
, uniformly in![]() . Let
. Let![]() ,
,![]() . When
. When![]() , then
, then
![]()
![]() uniformly in
uniformly in ![]() such that
such that![]() . ,
. ,
Proof. Let an error function ![]() be a nonnegative function on
be a nonnegative function on ![]() such that
such that ![]() when
when![]() . By continuity of
. By continuity of ![]() , uniformly in
, uniformly in ![]() there exists an increasing error function
there exists an increasing error function ![]() such that
such that ![]() for all
for all![]() . Let
. Let![]() . Evidently,
. Evidently, ![]() , and for a.e. t,
, and for a.e. t, ![]() a.s.3
a.s.3
Suppose by contradiction that some ![]() exists, such that, for each
exists, such that, for each![]() , there exist
, there exist ![]() such that, for
such that, for ![]()
![]() (66)
(66)
and![]() ,
,![]() . Now for a.e. t,
. Now for a.e. t, ![]() , so
, so![]() . Let
. Let![]() .
.
The set ![]() has full Lebesgue measure
has full Lebesgue measure![]() . Then there must exist
. Then there must exist ![]() such that
such that
![]() (67)
(67)
Now,
![]()
There exists an increasing concave error function![]() , see Lemma K below. Evidently, by Jensen’s inequality,
, see Lemma K below. Evidently, by Jensen’s inequality, ![]() .
.
So a subsequence ![]() of
of ![]() converges a.s. to zero, hence also
converges a.s. to zero, hence also ![]() converges a.s. to zero (
converges a.s. to zero (![]() is a.s. finite by the assumption on
is a.s. finite by the assumption on ![]() in the Lemma). Moreover,
in the Lemma). Moreover,
![]() ,
, ![]() being a
being a ![]() -function by the assumption on
-function by the assumption on ![]() in the Lemma. By dominated convergence
in the Lemma. By dominated convergence ![]() when
when![]() , and a contradiction of (67) is obtained. ,
, and a contradiction of (67) is obtained. ,
Lemma K. Let ![]() be an increasing error function. There exists an increasing concave error function
be an increasing error function. There exists an increasing concave error function ![]() such that
such that![]() .
.
Proof. Let ![]() and let
and let![]() . The set
. The set ![]() is compact. There is a line through
is compact. There is a line through ![]() with minimal positive slope touching
with minimal positive slope touching ![]() “to the left of”
“to the left of” ![]() at some perhaps nonunique point
at some perhaps nonunique point![]() ,
,![]() . Here, “touching” means that the line contains a point of
. Here, “touching” means that the line contains a point of![]() , but no point in
, but no point in ![]() lies strictly above the line. We choose
lies strictly above the line. We choose ![]() as large as possible (perhaps
as large as possible (perhaps![]() ). All points
). All points![]() ,
, ![]() , ly below or on the segment
, ly below or on the segment ![]() between
between ![]() and
and![]() . If
. If![]() , repeat the construction by replacing
, repeat the construction by replacing ![]() by
by![]() . The segment
. The segment ![]() so obtained between
so obtained between ![]() and some
and some![]() ,
, ![]() ,
, ![]() chosen as large as possible, has a slope strictly larger than the slope of
chosen as large as possible, has a slope strictly larger than the slope of![]() , otherwise
, otherwise ![]() would not be as large as possible. All points
would not be as large as possible. All points![]() ,
, ![]() , ly below or on the segment
, ly below or on the segment![]() . Continue this prosess. The points
. Continue this prosess. The points ![]() obtained equals
obtained equals ![]() for some increasing subsequence
for some increasing subsequence ![]() of
of ![]() Perhaps
Perhaps ![]()
![]() for some
for some![]() , or
, or ![]() for
for ![]() in which case
in which case![]() . The union of the segments
. The union of the segments ![]() forms the graph of an increasing concave error function
forms the graph of an increasing concave error function![]() . We have that the points
. We have that the points ![]() on the segments have the property that they “dominate” the points
on the segments have the property that they “dominate” the points ![]() in the sense that
in the sense that![]() , and for
, and for ![]() we have
we have![]() . Then for all
. Then for all![]() ,
, ![]() , for
, for![]() ,
, ![]() . (If
. (If ![]() , the segment
, the segment ![]() contains
contains ![]() as well as
as well as![]() , so
, so ![]() is linear on
is linear on ![]() and
and ![]() for
for![]() ,
,![]() .)
.)
Remark L (Proof of (29)) Let ![]() and let
and let![]() . Let
. Let ![]() and let
and let![]() . Then
. Then ![]() a.s. when
a.s. when ![]() as
as ![]() is a.s. finite, because
is a.s. finite, because![]() . Then
. Then ![]() a.s. and by Lebesgue’s dominated convergence theorem also in
a.s. and by Lebesgue’s dominated convergence theorem also in![]() . So
. So ![]() is
is ![]() -dense in
-dense in ![]() (and then also
(and then also ![]() -dense). Evidently,
-dense). Evidently, ![]() , moreover, as shown,
, moreover, as shown, ![]() , so
, so
![]() .
.
If![]() , then
, then ![]() by (57) in Appendix. If
by (57) in Appendix. If![]() ,
, ![]() , then
, then
![]()
so![]() . Because
. Because ![]() , then
, then ![]() ®
® ![]() in
in ![]() when (in
when (in![]() )
) ![]() ,
, ![]() , hence
, hence ![]() when
when![]() .
.
Now, ![]() when
when ![]() , by
, by![]() , and then
, and then ![]() in
in ![]() when
when ![]() in
in![]() ,
, ![]() ,
, ![]() , so
, so ![]() when
when ![]() . Moreover, by (57) in Appendix,
. Moreover, by (57) in Appendix, ![]() when
when![]() , so
, so ![]() when
when ![]() .
.
Hence ![]() as well as
as well as ![]() belong to
belong to ![]() when
when ![]() (
(![]() ).
).
Remark M (Completeness of![]() )
)
Evidenly, ![]() is complete, so a
is complete, so a ![]() -Cauchy-sequence
-Cauchy-sequence ![]() in
in ![]() is
is ![]() -convergent to some
-convergent to some![]() . Then for a subsequence
. Then for a subsequence![]() , for a.e. t,
, for a.e. t,![]() . From this we get that, for any
. From this we get that, for any![]() , if
, if ![]() when
when ![]() are large, then for a.e. t even
are large, then for a.e. t even![]() , so
, so![]() , which means that
, which means that ![]() is
is ![]() -complete.
-complete.
Remark N (![]() in
in ![]() -norm and a.s. when
-norm and a.s. when![]() ).
).
Let![]() , and let
, and let![]() . By weak compactness, a convex combination
. By weak compactness, a convex combination![]() ,
, ![]() ,
, ![]() , converges in
, converges in ![]() and also almost uniformly to some
and also almost uniformly to some ![]() -measurable limit4
-measurable limit4![]() , the latter convergence by considering subsequences if necessary. By
, the latter convergence by considering subsequences if necessary. By ![]() -convergence,
-convergence, ![]() evidently satisfies
evidently satisfies
![]() .
.
Let ![]() and
and ![]() be arbitrary, let M be a set on which
be arbitrary, let M be a set on which ![]() converges uniformly,
converges uniformly, ![]() , and let j be the smallest j such that
, and let j be the smallest j such that ![]() and
and![]() . Let
. Let![]() . Then, for
. Then, for![]() ,
, ![]() ,
, ![]() , using Jensens inequality twice,
, using Jensens inequality twice,
![]()
For![]() , this holds even for
, this holds even for![]() , yielding
, yielding ![]() -convergence of
-convergence of ![]() when
when![]() , using
, using ![]() yields almost uniform convergence.
yields almost uniform convergence.
Remark O. In this remark let “tr” mean tranpose. Note that ![]() (
(![]() ) and that, for
) and that, for![]() ,
, ![]() ,
,
![]()
Taking now ![]() to be a row vector, then
to be a row vector, then ![]() satisfies
satisfies ![]() . Letting
. Letting ![]() be the entities on pp. 348-350 in [6] , for
be the entities on pp. 348-350 in [6] , for![]() ,
, ![]() ,
, ![]() ,
, ![]() , we have that
, we have that![]() , and then
, and then ![]() by (2.20) in that book, so by (2.9) in that book, for some
by (2.20) in that book, so by (2.9) in that book, for some![]() ,
, ![]() satisfies (54),(55).
satisfies (54),(55).
Remark P (Proof of continuity of ![]() on
on ![]() ,
,![]() ).
).
Let![]() ,
, ![]() ,
, ![]() and let k be the smallest k such that
and let k be the smallest k such that![]() . Note that if
. Note that if![]() , then
, then![]() , for
, for![]() , and that
, and that![]() . Hence
. Hence ![]() . On the other hand
. On the other hand ![]() . Hence, on
. Hence, on![]() , the norms
, the norms ![]() and
and ![]() are equivalent. (Thus, the spaces
are equivalent. (Thus, the spaces![]() ,
, ![]() are subspaces of
are subspaces of![]() , in fact of
, in fact of![]() , because
, because ![]() -closure of
-closure of![]() .) For
.) For![]() , define
, define
![]() (68)
(68)
Then an application of Appendix, Lemma A gives that ![]() for some constant D independent of
for some constant D independent of![]() . Then
. Then
![]()
Because ![]() for
for![]() , then
, then
![]() (69)
(69)
Now, ![]() , so
, so![]() . For some constant
. For some constant![]() ,
, ![]() for
for![]() , so
, so ![]() ,
,![]() .
.
Remark Q (Proof of ![]() -continuity of
-continuity of![]() ,
,![]() ).
).
Let![]() , and fix
, and fix![]() . By Remark P,
. By Remark P, ![]() is
is ![]() -continuous in
-continuous in![]() , so there exists an
, so there exists an ![]() -function
-function![]() , such that
, such that![]() . Define
. Define![]() ,
,![]() . Note that
. Note that ![]() , so
, so ![]() is continuous because
is continuous because ![]() and
and ![]() is continuous (compare Theorem 6.14 p. 47 in [6] , a similar theorem holds for random coeffficients). Because
is continuous (compare Theorem 6.14 p. 47 in [6] , a similar theorem holds for random coeffficients). Because ![]() by Lemma A in Appendix,
by Lemma A in Appendix, ![]() is
is ![]() -continuous. Hence
-continuous. Hence ![]() is a.s. and
is a.s. and ![]() -continuous.
-continuous.
Evidently, for any![]() ,
,
![]()
Then, for any![]() ,
,
![]()
From this it follows that ![]() for all
for all![]() .
.
Let ![]() be given. Note that if
be given. Note that if ![]() and
and ![]() is (also) left continuous, then
is (also) left continuous, then ![]() in
in ![]() and a.s. , see Corollary A.9, Appendix C in [1] 5 and
and a.s. , see Corollary A.9, Appendix C in [1] 5 and ![]() in
in ![]() and a.s., see Remark N in Appendix, or, for both these results, Theorem 6.23 in [10] . Using this for
and a.s., see Remark N in Appendix, or, for both these results, Theorem 6.23 in [10] . Using this for ![]() and
and ![]() and continuity of
and continuity of ![]() yield that
yield that ![]() is a.s. and
is a.s. and ![]() -continuous, as we shall see: Fix any
-continuous, as we shall see: Fix any![]() . When
. When ![]() is close to s,
is close to s, ![]() . This is obvious for the
. This is obvious for the ![]() -norm, and also for a.s.-convergence, once we have shown that
-norm, and also for a.s.-convergence, once we have shown that ![]() almost uniformly. Note that by Egoroff’s theorem,
almost uniformly. Note that by Egoroff’s theorem, ![]() almost uniformly. Let
almost uniformly. Let ![]() . For any
. For any![]() , for some set
, for some set![]() , with
, with ![]() and some
and some![]() ,
, ![]() when
when![]() . By almost uniform convergence again, we can find a set
. By almost uniform convergence again, we can find a set![]() , with
, with ![]() and a
and a ![]() such that
such that ![]() when
when![]() . Defining
. Defining ![]() and
and![]() , we have
, we have ![]() and
and ![]() and hence
and hence ![]() when
when![]() . Thus,
. Thus,
![]()
when![]() . Then,
. Then,
![]()
So we have ![]() when
when ![]() and
and![]() . Now,
. Now, ![]() , and
, and
![]() . Hence,
. Hence,
![]() almost uniformly.
almost uniformly.
Remark R (Proof of (21)Þ (15), with![]() , when
, when![]() )
)
Let![]() . For any
. For any![]() , there exists a
, there exists a![]() , with
, with![]() ,
, ![]() (and with
(and with![]() ), such that
), such that ![]() and hence
and hence
![]()
Then for![]() , we have
, we have
![]()
note that![]() , so (15) holds for
, so (15) holds for![]() ,
,![]() .
.
Remark S. (Proof of (19)). Let u be any given element in U, ![]() , and let
, and let ![]() be an arbitrarily given Lebesgue point of
be an arbitrarily given Lebesgue point of![]() . Then, for any
. Then, for any![]() ,
, ![]() ,
,
![]() (70)
(70)
when![]() . We have
. We have ![]() , when
, when![]() , for
, for![]() . From this and (70) it follows that
. From this and (70) it follows that
![]()
Because ![]() was arbitrary, (19) follows for
was arbitrary, (19) follows for![]() , i.e. for a.e. t.
, i.e. for a.e. t.
Remark T. Let ![]() be a finite measure space. If
be a finite measure space. If ![]() (
(![]() Euclidean spaces) is continuous in x and
Euclidean spaces) is continuous in x and ![]() -measurable in
-measurable in![]() ,
, ![]() ,
, ![]() , and
, and ![]() in
in ![]() -measure, (
-measure, (![]() and
and ![]()
![]() -measurable), then
-measurable), then ![]() in
in![]() . This result, which is a special case of Krasnoselskii's theorem (see p. 20 in [9] ), can be proved as follows. By contradiction, assume for some
. This result, which is a special case of Krasnoselskii's theorem (see p. 20 in [9] ), can be proved as follows. By contradiction, assume for some ![]() and for some subsequence
and for some subsequence ![]() that
that ![]() for all j. A subsequence
for all j. A subsequence ![]() converges
converges ![]() -a.e. to
-a.e. to![]() . Then, by continuity,
. Then, by continuity, ![]()
![]() -a.e. and even in
-a.e. and even in![]() , by Lebesgue's dominated convergence theorem. A contradiction has been obtained.
, by Lebesgue's dominated convergence theorem. A contradiction has been obtained.
Remark U. (On![]() ,
,![]() )
)
On![]() ,
,![]() . To show this, for the component
. To show this, for the component ![]() of
of![]() , note that
, note that
![]()
![]()
so
![]()
Remark V. (Proof of (B) Þ (A) with ![]() in Remark 6)
in Remark 6)
Let![]() . By Lemma A in Appendix, for some
. By Lemma A in Appendix, for some![]() ,
, ![]() when
when![]() . Let
. Let
![]()
let ![]() satisfy
satisfy![]() , let
, let ![]() and let
and let![]() ,
, ![]() ,
, ![]() . By (B) in Remark 5, for any
. By (B) in Remark 5, for any![]() , any
, any![]() , for some progressively measurable
, for some progressively measurable![]() ,
, ![]() on
on![]() , for each
, for each![]() ,
, ![]() ,
,
![]()
where![]() , so
, so![]() . Hence, by slight abuse of notation, we have that
. Hence, by slight abuse of notation, we have that
![]()
By the choice of c, for![]() ,
,
![]()
By Remark W and the previous inclusion, then![]() , where
, where
![]()
Now, by definition of![]() , for
, for ![]() small,
small, ![]() and
and ![]() are
are ![]() when
when![]() , so
, so ![]() and
and![]() , so
, so ![]() , where
, where
![]()
Hence, (B) Þ (A) has been proved.
Let ![]() be the natural filtration, augmented as before. Postulating now (A), by Ito’s representation theorem,
be the natural filtration, augmented as before. Postulating now (A), by Ito’s representation theorem,
![]() , so by the linear interior mapping theorem, for some
, so by the linear interior mapping theorem, for some ![]() -ball
-ball ![]() in
in![]() ,
,![]() . But then
. But then ![]() .
.
Remark W. Let I be a set and let X be a normed space. Let the maps v and w from I into X have the following properties. Given![]() ,
, ![]() ,
, ![]() , assume that
, assume that ![]() and that
and that ![]() for all i. Then
for all i. Then![]() .
.
For a proof see p. 327 in [11] .
Remark X. (A nonzero continuous linear functional on ![]() vanishing on all
vanishing on all![]() ,
,![]() )
)
Let![]() ,
, ![]() the natural filtration corresponding to some given
the natural filtration corresponding to some given![]() . For simplicity, assume
. For simplicity, assume![]() . Choose a
. Choose a ![]() such that
such that![]() . Then
. Then![]() , so
, so ![]() belongs to the
belongs to the ![]() -boundary of the
-boundary of the ![]() -ball
-ball ![]() in
in![]() . Then for some nonzero continuous linear functional
. Then for some nonzero continuous linear functional ![]() on
on![]() ,
,![]() . Let
. Let ![]() and let k be any given integer such that
and let k be any given integer such that![]() . If
. If ![]() and
and![]() , then
, then ![]() for
for ![]() and
and ![]() for
for![]() , so
, so ![]() for all j (Þ
for all j (Þ![]() ). Then the inequality involving
). Then the inequality involving ![]() yields
yields![]() , i.e.
, i.e. ![]() vanishes on
vanishes on![]() ,
,![]() . To show in detail that such a
. To show in detail that such a ![]() exists, let
exists, let![]() ,
,
![]() . Then
. Then ![]() , so for
, so for![]() ,
, ![]() , and for
, and for![]() ,
, ![]() . Letting
. Letting ![]() , we get
, we get ![]() , so
, so ![]() and
and![]() .
.
Note that ![]() belongs to the
belongs to the ![]() -boundary of
-boundary of ![]() and the f's belong to
and the f's belong to![]() , so the arguments above actually yield a nonzero
, so the arguments above actually yield a nonzero ![]() -continuous linear functional on
-continuous linear functional on![]() , vanishing on all
, vanishing on all![]() ,
,![]() .
.
Remark Y. (![]() is nonempty).
is nonempty).
On ![]() define
define![]() , where
, where ![]() are some arbitrarily chosen sets such that
are some arbitrarily chosen sets such that![]() ,
,![]() . Then for all t,
. Then for all t, ![]() , so
, so ![]() and
and![]() . Now
. Now ![]() for all i, so
for all i, so ![]() for all i.
for all i.
Now![]() . Let us show that. Assume by contradiction that
. Let us show that. Assume by contradiction that ![]() for some
for some![]() . Using the projection of
. Using the projection of ![]() onto
onto ![]() as in E. in the proof of Theorem 1, we have for some progressively measurable
as in E. in the proof of Theorem 1, we have for some progressively measurable![]() , that
, that![]() ,
, ![]() ,
,![]() .
.
For all t,![]() . Then
. Then ![]() , or
, or![]() . Then
. Then ![]() where
where ![]() , otherwise (using
, otherwise (using![]() )
)
![]() . But then, for all i,
. But then, for all i, ![]() , contradicting
, contradicting![]() .
.
NOTES
1![]() *means restriction to
*means restriction to![]() .
.
2Lemma A applies for![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
3Note that![]() , for all
, for all![]() , so
, so ![]() which implies that
which implies that ![]() for a.e. t and hence, for a.e. t, that
for a.e. t and hence, for a.e. t, that ![]() a.s.
a.s.
4A.s. convergence of the component ![]() to
to![]() ,
, ![]() , means
, means ![]() for any given
for any given ![]() (a arbitrary), hence
(a arbitrary), hence![]() .
.
5If![]() , this corollary ensures only
, this corollary ensures only ![]() -convergence of
-convergence of ![]() to
to![]() , but also of
, but also of ![]() in
in ![]() (to
(to![]() , which means that
, which means that ![]() is equicontionuous,
is equicontionuous, ![]() (the countable additivity is uniform). Then
(the countable additivity is uniform). Then ![]() in
in![]() , because
, because![]() , so
, so ![]() is equicontionuous.
is equicontionuous.