Whether the CPT Symmetry Can Be Almighty Even in a Photon

Koji Nagata¹, Tadao Nakamura²

¹Department of Physics, Korea Advanced Institute of Science and Technology, Daejeon, Korea.
²Department of Information and Computer Science, Keio University, Yokohama, Japan.

DOI: 10.4236/oalib.1101806                

Abstract

As a trial, though thinking of general concepts, of our scientific challenge, we consider whether the Charge-Parity-Time (CPT) symmetry can be almighty even in a photon. This is the main aim of this paper. In what follows, we discuss our argumentations dividing the conjecture into two parts. Rotational invariance of physical laws is an accepted principle in Newton’s theory. We show that it leads to an additional constraint on local realistic theories with mixture of ten-particle Greenberger-Horne-Zeilinger state. This new constraint rules out such theories even in some situations in which standard Bell inequalities allow for explicit construction of such theories. This says new hypothesis to the number of ten. Next, it turns out Zermelo-Fraenkel set theory has contradictions. Further, the von Neumann’s theory has a contradiction by using ±1/. We solve the problem of von Neumann’s theory while escaping from all contradictions made by Zermelo-Fraenkel set theory, simultaneously. We assume that the results of measurements are . We assume that only and are possible. This situation meets a structure made by Zermelo-Fraenkel set theory with the axiom of choice. We result in the fact that it may be kept to perform the Deutsch-Jozsa algorithm even in the macroscopic scale because zero does not exist in this case. Our analysis agrees with recent experimental report.

Keywords

Quantum Measurement Theory, Formalism, Quantum Nonlocality, Quantum Computer

Subject Areas: Applied Physics

1. Introduction

These days, an interesting experimental research was reported [1] . Anti-photon is detected in the experiment. Further, constraints on relativity violations from gamma-ray bursts are reported [2] . We are detonated by them very much. So we present a theoretical conjecture to the violation of the Charge-Parity-Time (CPT) symmetry even in a photon. The CPT symmetry is a fundamental symmetry of physical laws under transformations that involve the simultaneous inversion of charge, parity, and time. This is a motivation of this paper. This is the schematic and keen objective of this paper.

The results of first argumentation, dealing with consequences for the assumption of rotational invariance for tests of non-locality, have been published [3] - [5] . Our intention is to engage with and expand upon these same results with mixture of ten-particle Greenberger-Horne-Zeilinger (GHZ) state [6] . In this argumentation, we present violation of the Bell inequality by mixture of ten-particle GHZ state in different bases and white noise. The inequality was derived by us in the argumentation cited as [7] . The same state, but for six spins, was also considered there.

Non-locality in quantum physics means the possibility of distributing correlations that cannot be due to previously shared randomness, without signaling [8] - [10] . Some quantum predictions violate Bell inequalities [11] , which form necessary conditions for local realistic theories for the results of measurements. Thus, some quantum predictions do not accept local realistic theories.

Leggett-type nonlocal realistic theory [12] is experimentally investigated [13] - [15] . The experiments report that the quantum theory does not accept Leggett-type nonlocal realistic theory. These experiments are performed

by using entangled states (two spins).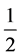

Rotational invariance of physical laws is a generally accepted principle in Newton’s theory. It states that the value of a correlation function does not depend on the coordinate systems used by the observers. The measure- ment setup classifies realistic theories [14] - [16] .

Many of the recent advances in quantum information theory suggest that the highly-non-local properties of quantum states that lead to violations of Bell inequalities can be used as a resource to achieve success in some tasks, which are locally impossible. Examples can serve quantum cryptography and quantum communication complexity [17] - [19] . Therefore as the impossibility of existence of local realistic theories for some processes leads to various quantum informational applications it is important to learn what the ultimate bounds for such theories are.

We aim to show that the fundamental property of the known laws of Newton’s theory, their rotational invariance can be used to find new hypothesis by using disqualification of experimentally accessible local rea- listic theories with ten particles in a new state.

This argumentation is as follows. Assume that we have some correlation function. This correlation function has a form which is rotationally invariant (cf. Equation (2)). We want to build rotationally invariant local realistic theory for the rotationally invariant correlation function. We see that the demand that the resulting correlation function must be rotationally invariant leads to a generalized Bell inequality [7] , which restricts additionally possible local realistic theories. Further, even if “standard” two-setting Bell inequalities [20] - [26] allow local realistic theories for the given set of data (i.e., a set of correlation function values obtained in a Bell type experiment), the new restriction, derived from rotational invariance, can invalidate such theories, for some range of parameters.

Next, we discuss von Neumann’s theory cannot meet the Deutsch-Jozsa algorithm. We discuss axiomatic theory has a contradiction. So we think that we give confusion to many scientists. Let confused scientists feel relieved by solving the problems mentioned above. We do not think that the solution is only one presented here. We think it is one of solutions. Let us start reviewing the axiomatic set theory.

Zermelo-Fraenkel set theory with the axiom of choice, commonly abbreviated ZFC, is the standard form of axiomatic set theory and as such is the most common foundation of mathematics. It has a single primitive ontological notion, that of a hereditary well-founded set, and a single ontological assumption, namely that all individuals in the universe of discourse are such sets. ZFC is a one-sorted theory in first-order logic. The signature has equality and a single primitive binary relation, a set membership, which is usually denoted Î. The formula 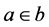means that the set a is a member of the set b (which is also read, “a is an element of b” or “a is in b”). Most of the ZFC axioms state that particular sets exist. For example, the axiom of pairing says that given any two sets a and b there is a new set containing exactly a and b. Other axioms describe properties of set membership. A goal of the ZFC axioms is that each axiom should be true if interpreted as a statement about the collection of all sets in the von Neumann universe (also known as the cumulative hierarchy). The metamathe- matics of ZFC has been extensively studied. Landmark results in this area established the independence of the continuum hypothesis from ZFC, and of the axiom of choice from the remaining ZFC axioms [27] . Mach literature concerning above topic can be seen in Refs. [28] - [44] . However, it turns out Zermelo-Fraenkel set theory has a contradiction [45] . Zermelo-Fraenkel set theory has a contradiction also by using zero. In fact there are two types of problems in Zermelo-Fraenkel set theory. Moreover von Neunann’s thoery does not meet mathematical formalism of quantum computation by using 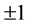[46] [47] . We propose changing measurement results into.

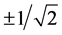There is a solution escaping from all of contradictions made by ZFC axioms and von Neumann’s theory for the Deutsch-Jozsa algorithm. A solution of von Neumann’s theory for the Deutsch-Jozsa algorithm have already published. So, we summarize this part to be included in this big paper.

We solve the problem of von Neumann’s theory while escaping from both contradictions made by Zermelo- Fraenkel set theory, simultaneously. We assume that the results of measurements are 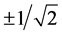[46] . We assume that only 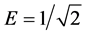and are possible. 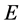is an expected value. This situation meets a structure made by Zermelo-Fraenkel set theory with the axiom of choice. An important note here, we can not avoid an established mathematical method presented in Refs. [45] - [47] if we accept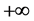. We want to introduce 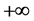and to define expected value.

In what follows, we discuss our argumentations dividing the conjecture into two parts.

This paper is organized as follows.

In Section 2, we discuss generalized Bell inequality.

In Section 3, we discuss mixture of ten-qubit GHZ state.

In Section 4, we discuss violation of rotational invariance of local realistic models with mixture of GHZ state.

In Section 5, we discuss summary of the first argumentation.

In Section 6, we discuss whether there are solutions of the problems of ZFC axioms and von Neumann’s theory for the Deutsch-Jozsa algorithm.

In Section 7, we discuss the first type of contradiction made by the axiomatic theory. This type of contra- diction is escapable by using max or min of possible values of expected value under study.

In Section 8, we discuss the second type of contradiction made by the axiomatic theory. This type of con- tradiction is escapable by assuming that zero does not exist.

In Section 9, we discuss the solution escaping from both of contradictions made by the axiomatic theory and von Neumann’s theory for the Deutsch-Jozsa algorithm.

In Section 10, we discuss the summary of the second argumentation.

In Section 11, we discuss implications of our argumentation.

Section 12 summarizes this paper.

2. Generalized Bell Inequality

Assume that we have a set of N spins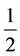. Each of them is in a separate laboratory. As is well known the

measurements (observables) for such spins are parameterized by a unit vector 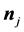(its direction along which the spin component is measured). The results of measurements are. We can introduce the “Bell” correlation function, which is the average of the product of the local results:

(1)

where is the local result, , which is obtained if the measurement direction is set at.

If an experimental correlation function admits rotationally invariant tensor structure familiar from Newton’s theory, we can introduce the following form:

(2)

where denotes the tensor product, the scalar product in, and the correlation tensor given by

(3)

where is a unit directional vector of the local coordinate system of the jth observer; gives the full set of orthogonal vectors defining the local Cartesian coordinates. Obviously the assumed form of (2) implies rotational invariance, because the correlation function does not depend on the coordinate systems used by the observers. Rotational invariance simply states that the value of cannot depend on the local coordinate systems used by the observers. There is an important, although obvious, implication of rotational invariance.

Assume that one knows the values of all components of the correlation tensor, , which are obtainable by performing specific measurements of the correlation function, (cf. Equation (3)). Then, with the use of formula (2) we can reproduce the value of the correlation functions for all other possible sets of local settings. Using this rotationally invariant structure of the correlation function, we shall derive a necessary condition for the existence of rotationally invariant local realistic theory of the experimental correlation function given in (2). If the correlation function is described by rotationally invariant local realistic theory, then the correlation function must be simulated by the following structure

(4)

where is some local hidden variable, is a probabilistic distribution, and is the pre- determined “hidden” result of the measurement of all the dichotomic observable with values. The dependence on the choice of the correlation function is unit vector.

Those assumptions are now demystify by Hess and Phillip [48] [49] , as they show that Bell’s inequalities may be violated even for objective local random variables.

Let us parametrize the arbitrary unit vector in a spherical coordinate system defined by, , and in the following way:

(5)

where, , and are the Cartesian axes relative to which spherical angles are measured.

We shall show that the scalar product of rotationally invariant local realistic correlation function

(6)

with the rotationally invariant experimental correlation function, that is

(7)

is bounded by a specific number dependent on, namely:

(8)

where is the maximal possible value of the correlation tensor component, i.e.,

(9)

We use decomposition (5). We introduce the usual measure for the system of the th observer. Note that, due to the integrations in (8), we are looking for rotationally invariant theory described by the entire range of settings. A necessary condition for the existence of rotationally invariant local realistic theory of the rotationally invariant experimental correlation function

(10)

that is for equal to, is that we have. If we have, e.g., , then the rotationally invariant experimental correlation function cannot be explainable by rotationally invariant local realistic theory.

In what follows, we derive the upper bound (8). Since the rotationally invariant local realistic theory is an average over, it is enough to find the bound of the following expression:

(11)

where

(12)

and

(13)

Let us analyze the structure of this integral (11). It is easy to notice that (11) is a sum, with coefficients given by, which is a product of the following integrals:

(14)

and

(15)

Notice that we deal here with integrals, or rather scalar products of with three orthogonal func- tions. Simply we have

(16)

The normalized functions, , and form a basis of a

three-dimensional real functional space, which we shall call. Using these three functions we can write the projection of function onto them such as

(17)

where is the length of the projection, and and are some angles. Going back to expression (11), we have

(18)

with a normalized vector

(19)

Note that the sum in (18) over the components of this vector is just, i.e., it is a component of the tensor in the local Cartesian coordinate systems specified by the vectors. If we know all the values of, we can always find the maximal possible value of such a component, and it is equal to, of Equation (9). Thus,

(20)

It remains to show the upper bound on the norm. From the definition the norm is given by a maximal

possible value of the scalar product between and any normalized function belonging to:

(21)

where and. Since, we have, for the integral of the modulus,

(22)

where the dot between three-dimensional vectors denotes the usual scalar product in. The values of this scalar product are then integrated (summed) over all values of and, i.e., over vectors on the whole sphere. Since the measure is rotationally invariant the integral does not depend on particular and we choose it as a unit vector in direction. For this choice

(23)

Finally, we have

(24)

The relation (24) is a generalized N-qubit Bell inequality with the entire range of measurement settings. Rotationally invariant local hidden variable theories, , which rebuild experimental rotationally invariant correlations, E, satisfy it. Below we show that if we replaces by we may have a violation of the inequality (24). We have

(25)

where we use the orthogonality relation. The structure of condition (24) and the value

(25) suggests that the value of (25) does not have to be smaller than (24). That is there may be such correlation functions, which have the property that for any we have, which implies im- possibility of modeling by rotationally invariant local realistic correlation function.

3. Mixture of Ten-Qubit GHZ State

We shall present an important quantum state. We assume. Consider the following ten-qubit Green- berger-Horne-Zeilinger (GHZ) state [6]

(26)

where is the eigenstate of the local operator of the jth observer. Note that the states of the last party are flipped with respect to the states of the other parties. We rotate the states of all individual qubits by the angle

around the axis on the Bloch sphere. This rotation cyclically permutes the direc-

tions of the Cartesian coordinate system. The unitary realizing this rotation is given by [50] :

(27)

with being a vector of local Pauli operators. Applying U to all the qubits gives a new state

. With the double application we get. The states and are, up to a

global phase which does not contribute to correlations, of the same form as, but are written in the local bases of and operators, respectively. Finally, we introduce a mixture of Greenberger-Horne-Zeilinger correlations and white noise:

(28)

where is the GHZ state and is the random noise admixture. The value of can be inter-

preted as the reduction factor of the interferometric contrast observed in the ten-particle correlation experiment.

4. Violation of Rotational Invariance of Local Realistic Models with Mixture of GHZ State

We present here a simple, but important example of violation (24). Imagine 10 observers who can choose between three orthogonal directions of spin measurement, , , and for the jth one.

Let us assume that the source of 10 entangled spin-carrying particles emits them in a state, which can be described as a mixture of Greenberger-Horne-Zeilinger correlations, given in (28). We can show that if the observers limit their settings to, , and, there are

(29)

components of of the value. Other x-y-z components vanish.

It is easy to see that

(30)

Then, we have and. It is clear that if we have ten

spins the rotational invariance puts an additional, non trivial, constraint on a local realistic theory. For given by

(31)

despite the fact that there exists a local realistic theory for the actually measured values of the correlation function, the rotational invariance principle disqualifies this theory. As it is shown in [26] if the correlation tensor satisfies the following conditions

(32)

then there always exists an explicit local realistic theory for the set of correlation function values

,. For our example the condition (32) is met whenever.

Nevertheless the rotational invariance principle excludes local realistic theories for. Thus the

situation is such for for all two settings per observer experiments we can construct a local realistic

theory for the values of the correlation function for the settings chosen in the experiment. But these theories must be consistent with each other, if we want to extend their validity beyond the 2¹⁰ settings to which each of

them pertains. Our result clearly indicates that this is impossible for That is, theories built

to reconstruct the 2¹⁰ data points, when compared with each other, must be inconsistent-therefore they are invalidated. The theories must contradict each other. In other words the explicit theories, given in [26] , work only for the specific set of settings in the given experiment, but cannot be extended to all settings. We utilize rotational invariance to show this.

Please note that all information needed to get this conclusion can be obtained in a three-orthogonal-settings- per-observer experiments with ten particles. Simply to get both the value of (25) and of it is enough to measure all values of,.

5. Summary of the First Argumentation

In summary of the first argumentation, we have shown that rotational invariance of physical laws leads to an additional constraint on local realistic theories with ten particles new state. This new constraint has ruled out such theories even in some situations in which standard Bell inequalities allow for explicit construction of such theories. The whole analysis has been performed without any additional mathematical assumptions on the form of local realistic theories.

The interesting feature is that Bell’s theorem rules out realistic interpretation of some quantum mechanical predictions, and therefore of quantum mechanics in general, provided one assumes locality. Locality is a con- sequence of the general symmetries of the Poincaré group of the Special Relativity Theory. However it is a direct consequence of the Lorentz transformations (boosts), as they define the light-cone. As our discussion shows a subgroup of the Poincaré group, rotations of the Cartesian coordinates, introduces an additional con- straint on the local realistic models.

The results presented are the result of the definition of, Equation (4), this type of hidden variable has been widely studied, see [48] [49] [51] - [58] and it is known that for this type of hidden variable is not compatible with the experimental results [54] . The great debate is that we can not describe the action of the hidden variable as in (4) for most cases, this has necessarily the case when we have a stochastic force acting on the system among others, see [48] [49] [55] - [58] .

6. Are There Solutions of the Problems of ZFC Axioms and von Neumann’s Theory for the Deutsch-Jozsa Algorithm?

There is a solution escaping from both contradictions made by ZFC axioms and von Neumann’s theory for the Deutsch-Jozsa algorithm. A solution of von Neumann’s theory for the Deutsch-Jozsa algorithm have already published. So, we summarize this part to be included in this big paper.

We solve the problem of von Neumann’s theory while escaping from both contradictions made by Zermelo- Fraenkel set theory, simultaneously. We assume that the results of measurements are [46] . We assume that only and are possible. E is an expected value. This situation meets a structure made by Zermelo-Fraenkel set theory with the axiom of choice. An important note here, we can not avoid an established mathematical method presented in Refs. [45] - [47] if we accept. We want to introduce and to define expected value.

7. First Type of Contradiction Made by Zermelo-Fraenkel Set Theory with the Axiom of Choice

First of all we discuss a contradiction made by Zermelo-Fraenkel set theory with the axiom of choice. Assume all axioms of Zermelo-Fraenkel set theory with the axiom of choice is true. We consider statistics. We assume that the results of measurements are. We consider an average of these. We consider an expected value. We assume

(33)

We derive the possible value of the product (the square of mean) of the expected value. It is

(34)

Thus we have the following proposition when

(35)

The expected value which is the average of the results of measurements is given by

(36)

We assume that the possible values of the actually measured result are. We have

(37)

Same expected value is given by

(38)

We only change the labels as and. The possible values of the actually measured result are. By using these facts we derive a necessary condition for the expected value given in (36). We derive the possible values of the product of the expected value given in (36). We have

(39)

We derive a proposition concerning the expected value given in (36) under the assumption that the possible values of the actually measured result are which means. We derive the following proposition

(40)

We do not assign the truth value “1” for two propositions (35) and (40) simultaneously if. Thus we are in a contradiction if. This contradiction is escapable when or.

8. Second Type of Contradiction Made by Zermelo-Fraenkel Set Theory with the Axiom of Choice

Assume all axioms of Zermelo-Fraenkel set theory with the axiom of choice is true. We assume zero exists. We consider statistics. We assume that the results of measurements are. We consider an average of these. We consider an expected value E. We assume the number of is equal to the number of. Thus,

(41)

We derive the possible value of the product (the square of mean) of the expected value. It is

(42)

Thus we have the following proposition when

(43)

The expected value which is the average of the results of measurements is given by

(44)

We assume that the possible values of the actually measured result are. Same expected value is given by

(45)

We only change the labels as and. The possible values of the actually measured result are. Since the number of is equal to the number of, we have same expected value as follows

(46)

By using these facts we derive a necessary condition for the expected value given in (44). We derive the possible values of the product of the expected value given in (44). We have

(47)

We derive a proposition concerning the expected value given in (44) under the assumption that the possible values of the actually measured result are which means. We derive the following proposition

(48)

We do not assign the truth value “1” for two propositions (43) and (48) simultaneously. Thus we are in a contradiction due to assuming that zero exists. This type of contradiction is escapable if we skip zero.

9. Solution of the Contradiction

We assume zero does not exist. Thus we escape from the second type of contradiction made by Zermelo- Fraenkel set theory with the axiom of choice. We assume that the results of measurements are. We consider an average of these. We consider an expected value. We can assume two possible values of expected value

(49)

We assume the possible value of the product of the expected value. It can be assumed as

(50)

We assume the following proposition:

(51)

This expected value which can be the average of the results of measurements is given by

(52)

We assume that the possible values of the actually measured result are. We can assume

(53)

Same expected value can be given by

(54)

We change the labels as and. The possible values of the actually measured result are. By using these assumptions we try to derive a necessary condition for the expected value given in (52). We can derive the possible values of the product of the expected value given in (52). We can have

(55)

We can derive a proposition concerning the expected value given in (52) under the assumption that the possible values of the actually measured result are. which means. We can derive the following proposition

(56)

We can assign the truth value “1” for two propositions (51) and (56) simultaneously. We are not in a con- tradiction. Thus we escape from the first type of contradiction made by Zermelo-Fraenkel set theory with the axiom of choice.

One of wrong point of the axiomatic set theory is assuming zero. So we do not assume the existence of zero. Also the wrong point of von Neumann’s theory for quantum computation is assuming the results of measure- ments are. So we do not assume the results of measurement are.

10. Summary of the Second Argumentation

In summary of the second argumentation, one of wrong point of the axiomatic set theory has been assuming zero. So we do not have assumed the existence of zero. Also the wrong point of von Neumann’s theory for quantum computation has been assuming the results of measurements are. So we do not have assumed the results of measurements are. We have solved the problem of von Neumann’s theory and escaped from a contradiction made by Zermelo-Fraenkel set theory, simultaneously. We have assumed that the results of measurements are. We have assumed that only and are possible. This situation have met a structure made by Zermelo-Fraenkel set theory with the axiom of choice. It has been interesting that the conclusion in this argumentation agrees with recent research [46] . Of course, we have resulted in the fact that it may be kept to perform the Deutsch-Jozsa algorithm even in the macroscopic scale because zero does not exist in this case.

11. Discussions

We have concluded the following with discussions: Our discussion implies that there will be some mass for a photon. Since there is not zero, the mass will not be zero. Now the speed of the photon is finite. We suspect that some fields give resistance to the photon at this stage. In the future the mass will be increased so that we can see it experimentally.

We find there is not system of units in physics because there is not. We suspect everything is changeable. It is very important to find out mass of neutrinos.

Also we think it is dangerous to define subtraction. It may be introducing a contradiction to axiomatic set theory.

We would expect that the big-bang hypothesis would be true. We would then infer that the particle antiparticle pair would be constructed. The number of particles would be two. This would disqualify of a local realistic model with two particles due to quantum effect (Violation Charge). Then the voluntary violation of time symmetry would be true, so that the number of particles would be six. This would disqualify of a local realistic model with six particles due to quantum effect (Violation Time). Then the voluntary violation of the constant value of gravity would be true. Finally we would infer that the number of particles here would be ten. This would disqualify of a local realistic model with ten particles due to quantum effect as well (Violation Parity).

The Charge, Parity, and Time (CPT) symmetry would be violated. We know such results of experiments [2] .

An important conjecture is that a photon and an anti-photon pair collapse. Since the photon would be massive, it is theoretically possible. It is believed that the spin of a photon has. After the collapse the spin of a photon would be. The spin of an anti-photon would be. Of course, spin speed would not be 0.

It is interesting to create by using optical fiber device, which is something like that an electric current flows. If so, we would create new computer device by using optical fiber. We do not know what the device likes.

Finally, we point out spin is derived in our second argumentations. It is interpreted as a minimum spin of an elementary particle. One measurement is nonsense. Two measurements have meaning. It is important principle of statistics mathematics.

12. Conclusion

In conclusions, we have presented a theoretical conjecture of violation of the CPT symmetry even in a photon. This has been the main aim of this paper. We have discussed our argumentations dividing the conjecture into two parts. Rotational invariance of physical laws has been an accepted principle in Newton’s theory. We have shown that it leads to an additional constraint on local realistic theories with mixture of ten-particle Greenberger- Horne-Zeilinger state. This new constraint has ruled out such theories even in some situations in which standard Bell inequalities allow for explicit construction of such theories. Recently, it has turned out Zermelo-Fraenkel set theory has a contradiction. Further, the von Neumann’s theory has had a contradiction by using. Zermelo- Fraenkel set theory has had a contradiction also by using zero. We have solved the problem of von Neumann’s theory while escaping from both contradictions made by Zermelo-Fraenkel set theory, simultaneously. We have assumed that the results of measurements are. We have assumed that only and are possible. This situation has met a structure made by Zermelo-Fraenkel set theory with the axiom of choice. We have resulted in the fact that it may be kept to perform the Deutsch-Jozsa algorithm even in the macroscopic scale because zero does not exist in this case.

Acknowledgements

We thank Professor K. Niizeki and Dr. C.-L. Ren for valuable discussions.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Yokota, K., Yamamoto, T., Koashi, M. and Imoto, N. (2009) Direct Observation of Hardy’s Paradox by Joint Weak Measurement with an Entangled Photon Pair. New Journal of Physics, 11, Article ID: 033011. http://dx.doi.org/10.1088/1367-2630/11/3/033011
[2]	Kostelecky, V.A. and Mewes, M. (2013) Constraints on Relativity Violations from Gamma-Ray Bursts. Physical Review Letters, 110, Article ID: 201601. http://dx.doi.org/10.1103/PhysRevLett.110.201601
[3]	Nagata, K., Laskowski, W., Wieśniak, M. and Żukowski, M. (2004) RotationalInvariance as an Additional Constraint on Local Realism. Physical Review Letters, 93, Article ID: 230403. http://dx.doi.org/10.1103/PhysRevLett.93.230403
[4]	Nagata, K. and Ahn, J. (2008) Violation of Rotational Invariance of Local Realistic Models with Two Settings. Journal of the Korean Physical Society, 53, 2216.
[5]	Nagata, K. and Ahn, J. (2008) The Conflict between Bell-Żukowski Inequality and Bell-Mermin Inequality. Modern Physics Letters A, 23, 2967. http://dx.doi.org/10.1142/S0217732308028727
[6]	Greenberger, D.M., Horne, M.A. and Zeilinger, A. (1989) Going Beyond Bell’s Theorem. In: Kafatos, M., Ed., Bell’s Theorem, Quantum Theory and Conceptions of the Universe, Kluwer Academic, Dordrecht, 69-72. http://dx.doi.org/10.1007/978-94-017-0849-4_10
[7]	Nagata, K. (2007) Multipartite Omnidirectional Generalized Bell Inequality. Journal of Physics A: Mathematical and Theoretical, 40, 13101. http://dx.doi.org/10.1088/1751-8113/40/43/017
[8]	Redhead, M. (1989) Incompleteness, Nonlocality, and Realism. 2nd Impression, Clarendon Press, Oxford.
[9]	Peres, A. (1993) Quantum Theory: Concepts and Methods. Kluwer Academic, Dordrecht.
[10]	Einstein, A., Podolsky, B. and Rosen, N. (1935) Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Physical Review, 47, 777. http://dx.doi.org/10.1103/PhysRev.47.777
[11]	Bell, J.S. (1964) On the Einstein Podolsky Rosen Paradox. Physics, 1, 195-200.
[12]	Leggett, A.J. (2003) Nonlocal Hidden-Variable Theories and Quantum Mechanics: An Incompatibility Theorem. Foundations of Physics, 33, 1469-1493. http://dx.doi.org/10.1023/A:1026096313729
[13]	Gröblacher, S., Paterek, T., Kaltenbaek, R., Brukner, Č., Żukowski, M., Aspelmeyer, M. and Zeilinger, A. (2007) An Experimental Test of Non-Local Realism. Nature, 446, 871-875. http://dx.doi.org/10.1038/nature05677
[14]	Paterek, T., Fedrizzi, A., Gröblacher, S., Jennewein, T., Żukowski, M., Aspelmeyer, M. and Zeilinger, A. (2007) Experimental Test of Nonlocal Realistic Theories without the Rotational Symmetry Assumption. Physical Review Letters, 99, Article ID: 210406. http://dx.doi.org/10.1103/PhysRevLett.99.210406
[15]	Branciard, C., Ling, A., Gisin, N., Kurtsiefer, C., Lamas-Linares, A. and Scarani, V. (2007) Experimental Falsification of Leggett’s Nonlocal Variable Model. Physical Review Letters, 99, Article ID: 210407. http://dx.doi.org/10.1103/PhysRevLett.99.210407
[16]	Nagata, K. (2008) Classification of Local Realistic Theories. Journal of Physics A: Mathematical and Theoretical, 41, Article ID: 155308. http://dx.doi.org/10.1088/1751-8113/41/15/155308
[17]	Ekert, A.K. (1991) Quantum Cryptography Based on Bell’s Theorem. Physical Review Letters, 67, 661-663. http://dx.doi.org/10.1103/PhysRevLett.67.661
[18]	Scarani, V. and Gisin, N. (2001) Quantum Communication between N Partners and Bell’s Inequalities. Physical Review Letters, 87, Article ID: 117901. http://dx.doi.org/10.1103/PhysRevLett.87.117901
[19]	Brukner, Č., Żukowski, M., Pan, J.-W. and Zeilinger, A. (2004) Bell’s Inequalities and Quantum Communication Complexity. Physical Review Letters, 92, Article ID: 127901. http://dx.doi.org/10.1103/PhysRevLett.92.127901
[20]	Mermin, N.D. (1990) Extreme Quantum Entanglement in a Superposition of Macroscopically Distinct States. Physical Review Letters, 65, 1838-1840. http://dx.doi.org/10.1103/PhysRevLett.65.1838
[21]	Roy, S.M. and Singh, V. (1991) Tests of Signal Locality and Einstein-Bell Locality for Multiparticle Systems. Physical Review Letters, 67, 2761-2764. http://dx.doi.org/10.1103/PhysRevLett.67.2761
[22]	Ardehali, M. (1992) Bell Inequalities with a Magnitude of Violation That Grows Exponentially with the Number of Particles. Physical Review A, 46, 5375-5378. http://dx.doi.org/10.1103/PhysRevA.46.5375
[23]	Belinskii, A.V. and Klyshko, D.N. (1993) Interference of Light and Bell’s Theorem. Physics-Uspekhi, 36, 653-693. http://dx.doi.org/10.1070/PU1993v036n08ABEH002299
[24]	Werner, R.F. and Wolf, M.M. (2001) All-Multipartite Bell-Correlation Inequalities for Two Dichotomic Observables per Site. Physical Review A, 64, Article ID: 032112. http://dx.doi.org/10.1103/PhysRevA.64.032112
[25]	Werner, R.F. and Wolf, M.M. (2001) Bell Inequalities and Entanglement. Quantum Information & Computation, 1, 1-25.
[26]	Żukowski, M. and Brukner, Ű. (2002) Bell’s Theorem for General N-Qubit States. Physical Review Letters, 88, Article ID: 210401.
[27]	Zermelo-Fraenkel Set Theory—Wikipedia, the Free Encyclopedia.
[28]	Abian, A. (1965) The Theory of Sets and Transfinite Arithmetic. W. B. Saunders, Philadelphia.
[29]	Abian, A. and LaMacchia, S. (1978) On the Consistency and Independence of Some Set-Theoretical Axioms. Notre Dame Journal of Formal Logic, 19, 155-158. http://dx.doi.org/10.1305/ndjfl/1093888220
[30]	Devlin, K. (1996) The Joy of Sets. Springer, New York.
[31]	Fraenkel, A., Bar-Hille, Y. and Levy, A. (1973) Foundations of Set Theory. Fraenkel’s Final Word on ZF and ZFC, North Holland.
[32]	Hatcher, W. (1982) The Logical Foundations of Mathematics. Pergamon, London.
[33]	Jech, T. (2003) Set Theory. The Third Millennium Edition, Revised and Expanded, Springer, Berlin.
[34]	Kunen, K. (1980) Set Theory: An Introduction to Independence Proofs. Elsevier, Amsterdam.
[35]	Montague, R. (1961) “Semantic Closure and Non-Finite Axiomatizability” in Infinistic Methods. Pergamon, London, 45-69.
[36]	Suppes, P. (1972) Axiomatic Set Theory. Dover Reprint. Perhaps the Best Exposition of ZFC before the Independence of AC and the Continuum Hypothesis, and the Emergence of Large Cardinals. Includes Many Theorems.
[37]	Takeuti, G. and Zaring, W.M. (1971) Introduction to Axiomatic Set Theory. Springer Verlag, New York.
[38]	Tarski, A. (1939) On Well-Ordered Subsets of Any Set. Fundamenta Mathematicae, 32, 176-183.
[39]	Tiles, M. (2004) The Philosophy of Set Theory. Dover Reprint. Weak on Metatheory; the Author Is Not a Mathematician.
[40]	Tourlakis, G. (2003) Lectures in Logic and Set Theory. Volume 2, Cambridge University Press, Cambridge.
[41]	van Heijenoort, J. (1967) From Frege to Godel: A Source Book in Mathematical Logic, 1879-1931. Harvard University Press, Cambridge.
[42]	Zermelo, E. (1908) Untersuchungen uber die Grundlagen der Mengenlehre I. Mathematische Annalen, 65, 261-281. http://dx.doi.org/10.1007/BF01449999
[43]	van Heijenoort, J. (1967) Investigations in the Foundations of Set Theory. In: van Heijenoort, J., Ed., From Frege to Godel: A Source Book in Mathematical Logic, 1879-1931, Harvard University Press, Cambridge, MA, 199-215.
[44]	Zermelo, E. (1930) Uber Grenzzablen und Mengenbereiche. Fundamenta Mathematicae, 16, 29-47.
[45]	Nagata, K. and Nakamura, T. (2011) Does Singleton Set Meet Zermelo-Fraenkel Set Theory with the Axiom of Choice? Advanced Studies in Theoretical Physics, 5, 57.
[46]	Nagata, K. and Nakamura, T. (2010) Can von Neumann’s Theory Meet the Deutsch-Jozsa Algorithm? International Journal of Theoretical Physics, 49, 162-170. http://dx.doi.org/10.1007/s10773-009-0189-5
[47]	Nagata, K., Ren, C.-L. and Nakamura, T. (2011) Whether Quantum Computation Can Be Almighty. Advanced Studies in Theoretical Physics, 5, 1-14.
[48]	Hess, K. and Philipp, W. (2002) Exclusion of Time in the Theorem of Bell. Europhysics Letters (EPL), 57, 775-781. http://dx.doi.org/10.1209/epl/i2002-00578-y
[49]	Hess, K. and Philipp, W. (2005) The Bell Theorem as a Special Case of a Theorem of Bass. Foundations of Physics, 35, 1749-1767. http://dx.doi.org/10.1007/s10701-005-6520-y
[50]	Nielsen, M.A. and Chuang, I.L. (2000) Quantum Computation and Quantum Information. Cambridge University Press, Cambridge.
[51]	Gudder, S.P. (1980) Proposed Test for a Hidden Variables Theory. International Journal of Theoretical Physics, 19, 163-168. http://dx.doi.org/10.1007/BF00669767
[52]	Ballentine, L.E. (1990) Quantum Mechanics. Prentice-Hall, Englewood Cliffs.
[53]	Zimba, J.R. and Clifton, R.K. (1998) Valuations on Functionally Closed Sets of Quantum Mechanical Observables and von Neumann’s “No-Hidden-Variables” Theorem. In: Dieks, D. and Vermaas, P., Eds., The Modal Interpretation of Quantum Mechanics, Kluwer Academic Publishers, Dordrecht, 69-101.
[54]	Genovese, M. (2007) Research on Hidden Variable Theories: A Review of Recent Progresses. http://arxiv.org/abs/quant-ph/0701071
[55]	Aspect, A., Dalibard, J. and Roger, G. (1982) Experimental Test of Bell’s Inequalities Using Time-Varying Analyzers. Physical Review Letters, 49, 1804-1807. http://dx.doi.org/10.1103/PhysRevLett.49.1804
[56]	Hellmuth, T., Walther, H., Zajonc, A. and Schleich, W. (1987) Delayed-Choice Experiments in Quantum Interference. Physical Review A, 35, 2532-2541. http://dx.doi.org/10.1103/PhysRevA.35.2532
[57]	Kwiat, P.G. (1998) Experimental and Theoretical Progress in Interaction-Free Measurements. Physica Scripta, T76, 115. http://dx.doi.org/10.1238/Physica.Topical.076a00115
[58]	Cristian, J. (2007) Disproof of Bell’s Theorem by Clifford Algebra Valued Local Variables. http://arxiv.org/abs/quant-ph/0703179