1. Introduction
Rhotrix theory is a relatively new area of Mathematics, whose goal is central on representing arrays of numbers in rhomboid mathematical form, unlike matrix theory dealing with representing array of numbers in rectangular form. The concept of rhotrices of size three, also well known as base rhotrices, was introduced by Ajibade [1] as an extension of ideas on matrix-tertion and matrix-noitret, suggested by Atanassov and Shannon [2] .
Expressing rhotrices of size n, particularly in a generalized form, has been a difficult problem to the rhotrix theorist. This may probably be the reason, why most works in rhotrix theory are communicated using rhotrices of specific size; one can see [1] [3] -[6] . Though, some attempts were made by Sani [8] and Mohammed et al. [7] to overcome such problem in literature, but the two generalizations proposed by these authors are sometimes inconvenient for presenting rhotrices as two dimensional objects.
Thus, it becomes imperative to seek for a new method of generalizing expression for rhotrices in order to allow for exactness, efficiency and convenience in presentation of research results. Furthermore, better algebra and analysis of rhotrix theory can be studied using multiple array technique as proposed in this article.
2. An Overview of Initial Generalized Rhotrix Expressions
2.1. Coupled Matrix Technique for Expressing Rhotrix in a Generalized Form
In an attempt to find an answer to the problem of “finding a transformation of rhotrix to matrix and vice versa” posed by Ajibade [1] in the concluding remark of his article, Sani [8] proposed an alternative method for multiplication of rhotrices of size 3, based on their rows and columns vectors, as comparable to matrices, recorded as follows:
This alternative multiplication approach was also used in his work to establish some relationships between rhotrices of size 3 and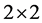 
dimensional matrices through an isomorphism. Thereafter, Sani [9] extend his own method for multiplication of base rhotrices to higher size rhotrices in form of generalization, recorded as follows:
where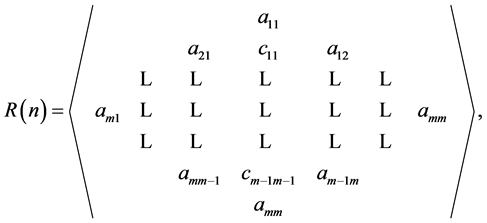 
and 
represent the 
and 
elements respectively, 
with 
and 
This idea of expressing rhotrix of size n, 
, as a combination of two matrices, was later presented as an idea for conversion of a rhotrix to a special form of a matrix, termed “coupled matrix” in Sani [10] . That is, a rhotrix R of size n can be expressed as a couple of two matrices A and C of sizes 
and 
respectively, where
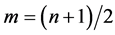and
.
It is noteworthy to mention that, this method presented by Sani for expressing rhotrix in a generalised form, requires some form of transformation or half transpose, in order to identify the rows and columns for any given rhotrix. Also, unique expression for the “rhotrix heart” cannot be deduced and therefore, this method of rhotrix expression is unsuitable for presenting heart-based rhotrices.
2.2. Single Array Technique for Expressing Rhotrix in a Generalized Form
Mohammed et al. [7] employ a single dimensional array routine for expressing real rhotrices of size n in a generalised form, recorded as follows:
where 
and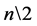 
is the integer value from division of n by 2. The entry 
is called the heart of any rhotrix
. The operations of addition, scalar multiplication and multiplication (o) with respect to this generalization were discussed in [7] .
At this point, it is necessary to point out that this method of expressing rhotrices in generalized form follow the initial definition given for rhotrices in [1] but it can only be functional on computing machines using single array procedure, which is inadequate and capable of causing slow processing of operations involving rhotrices having the same bigger size. Also, entries in rhotrices cannot be immediately indicated.
3. A New Generalized Expression for Rhotrix
Since rhotrix theory is a relatively new paradigm of matrix theory, finding a generalized expression that precisely represents rhotrices of the same size n, while preserving row and column entries, cannot be divorced from multiple array indexes as obtainable in matrices. For this reason, an adoption of the procedure that is analogous to representation of matrices will be utilized.
For example, consider a zero heart rhotrix A of size n = 5 given below;
Clearly, if we use comparison with matrix row and column entries then by observation, the entry value 1 in rhotrix A can be found at row 1 and column 3; the entry value 8 in rhotrix A can be found at row 2 and column 4; the entry value-4 in rhotrix A can be located at row 4 and column 2; the entry value 0 in rhotrix A can be located at row 3 and column 3; and the entry value 8 in rhotrix A can be found at row 5 and column 3. Thus, we can adopt this procedure to give a new expression for the rhotrix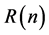
.
Let 
be the set of all rhotrices of size n over a field F (real or complex). Since any rhotrix 
has total number of entries as
, where 
then a technique for expressing the set of all rhotrices of the same size n in a generalized form is given by
(1)
where,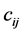 
are entries from a field of real or complex numbers F. It is clear that any entry 
in B(n) must be indicated by 
row and 
column. This method of expressing rhotrices in a general form is analogous to that of matrices because any entry 
within a rhotrix is indicated out by its row i and column j, which is analogous to any entry xij in matrix set X of all 
dimensional matrices, denoted by
.
From Equation (1), 
is called the heart of any rhotrix
.
Thus, for n = 3, we get 
and for n = 5, we get
.
Operations in Rhotrix Space over the New Expression
Let R and S be two rhotrices of the same size n and let 
be a scalar. If we denote the entries in rhotrix R as 
and the entries in rhotrix S as
, then we can extend the operations of addition, scalar multiplication and multiplication (o) defined for heart-base rhotrices of size-3 in [1] to rhotrices of the same n-size, using the rhotrix new expression respectively as follows:
and
where,
; 
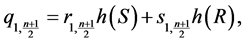
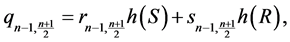
and 
The rhotrix set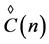 
together with above operations of addition
, scalar multiplication 
and multiplication 
is a generalization of rhotrix spaces, denoted by the pair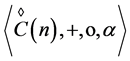
.
4. Conclusion
We have presented a statement of expression for generalization of all rhotrices of same size-n using multiple array indexes, which may be analogous to what is obtainable in matrix theory. The new rhotrix look will encourage the study of algebra and analysis of rhotrix spaces from a better perspective. In addition, computing efficiency and accuracy will also be improved, particularly when the operations over rhotrix spaces, based on the new expression are algorithmatized for computing machines. In the future research direction, it seems interesting to think of “axiomatization of real rhotrix space”. This topic will be our next line of focus for research.
Acknowledgements
We wish to thank Ahmadu Bello University, Zaria, Nigeria for funding this relatively new area of research.