Location Based Generalized Akash Distribution: Properties and Applications ()
1. Introduction
Several standard base-line distributions are available to model the lifetime data and the failure rate function is considered as the most crucial factor for these models. Examples of such distributions are exponential, gamma, Weibull, and log-normal distributions which have different capabilities to describe the shapes of the failure rate function. While the exponential distribution has a constant failure rate, the gamma and Weibull distributions have both increasing and decreasing failure rates [1]. Researchers in the recent past have an increased interest in modifications of the above-mentioned standard distributions to handle a complicated task for the modeling of lifetime data. The finite mixture models that consist of a weighted sum of the standard or modifications of standard distributions are popular to handle the complexity by heterogeneity in a lifetime data analysis. Each finite mixture failure rate may have various characteristics, such as monotonically increasing or decreasing, non-monotonic, constant, and bathtub shapes, and they may cover various tail-heaviness of a data set. We can measure the tail-heaviness of a data set by the excess kurtosis (EK) that is defined as
, where
is the kurtosis of the data set. The
is called as heavy-tailed (Leptokurtic) and
is called light-tailed (Platykurtic) distributions. Some notables are mentioned as, Hussaini, Dayian, and Adham (2000) introduced a two-component Gompertz lifetime model [2]; Marin, Berna, and Wiper (2005) obtained the Weibull mixture distributions [3]; Balakrishnan, Leiva, Sanhueza, and Cabrera (2009) proposed a mixture of inverse Gaussian distribution [4]; Erisoglu, Erisoglu, and Erol (2011) introduced a mixture model of two different distributions approach [5]; among others. However, more finite mixtures are complicated in their mathematical forms.
Another classical finite mixture model under the Bayesian framework is the Lindley distribution (LD) which is a finite mixture of two non-identical distributions, exponential and gamma distributions. It was introduced by Lindley (1958) [6] [7] having the density function:
(1)
where
is the shape parameter, and
is the respective random variable. Equation (1) presents two-component mixture of exponential (
) and gamma
(
) distributions with the mixing proportion
. The statistical properties of LD have discussed by Ghitany, Atieh, and Nadarajah (2008) and showed
that the Lindley distribution is more flexible and provides a better fit than the exponential distribution for lifetime data [8].
A considerable number of modifications of LD have been proposed by researchers with actual mixing components of LD based on the two-component mixture of exponential (
) and gamma (
) with different mixing proportions. Some notables are mentioned as, Shanker and Sharma (2013) proposed a two-parameter Lindley distribution [9]; Shanker and Mishra (2013) obtained the Quasi Lindley distribution [10]; Shanker (2015) introduced the Shanker distribution [11]; and Shanker, Shukla, and Tekie (2017) introduced a three-parameter Lindley distribution [12], and abbreviations of these distributions are TwPLD, QLD, SD, and ThPLD, respectively.
To increase more flexibility in this line of developments, Monsef (2016) [13] introduced a new three-parameter family Lindley distribution called Lindley with location distribution (LwLD) by adding the location parameter. The density function of this distribution is given by:
(2)
where
and
are shape parameters and
is a location parameter. Equation (2) presents two-component mixture of an exponential (
) and gamma
(
) distributions with the mixing proportion
.
On the other hand, Shanker (2015) [14] has obtained Akash distribution (AD) as an alternative to Lindley distribution with density function:
(3)
where
is a shape parameter. Equation (3) shows two-component mixture of
exponential (
) and gamma (
) with mixing proportion
.
Table 1 summarizes the above-mentioned existing Lindley family distributions’ names, abbreviations, parameters, shapes of the failure rate function, and references.
In many lifetime distributions, the location parameter may be assumed to be zero. However, the location parameter is an important parameter that provides an estimate of the failure-free period, that is the earliest time at which a failure may be observed. When we include the location parameter in a distribution, it changes the starting point of the distribution. For example, time to achieve pain relief in a patient after who has applied with a treatment method does not start from the value of zero. Then, in this application, the location parameter of the relevant distribution cannot be taken as zero.
![]()
Table 1. Distributions’ names, abbreviations, parameters, shapes of the failure rate function, and references.
In this paper, we introduce and study a new three-parameter Lindley family distribution with location parameter as a modification of AD. The new distribution will be called as location based generalized Akash distribution (NGAD). The NGAD is a two-component mixture of exponential and gamma distributions which generalizes the AD. Further, a simulation study will be done to study the performance of the ML method in the parameter estimation of the NGAD.
The remaining part of this paper is organized as follows: In Section 2, we introduce the NGAD with its density and distribution functions. We present the statistical and reliability properties of NGAD in Section 3 and Section 4, respectively. The size-biased form of the NGAD is discussed in Section 5. Further, the estimation of the parameters of NGAD by using the ML method is discussed in Section 6. Finally, a simulation study is done to study the performance of the maximum likelihood estimators for NGAD, and real-world applications are used to illustrate its flexibility with the above-mentioned existing modified Lindley distributions.
2. Location Based Generalized Akash Distribution
In this section, we introduce the location based generalized Akash distribution with its probability density function (pdf) and cumulative distribution function (cdf). Note that the Akash distribution (3) contains only one shape parameter. To develop the new distribution first, we define a new three-parameter Lindley family distribution by including the location parameter
as a finite mixture of
exponential (
) and gamma (
) with mixing proportion
under the Bayesian framework, as follows:
where,
and
are shape parameters and
, and
.
Then, the pdf of the NGAD with parameters
and
is defined by:
(4)
The range of the parameters is based on the log-likelihood function. Then, NGAD has one additional shape parameter and the location parameter compared to AD's parameter. Plots in Figure 1 have drawn by fixing 2 parameters and changing the 3rd parameter. Figure 1 shows how the shape parameters
and
affect the shape of the NGAD and how the location parameter affects the starting point of the distribution. Here, we may observe that the pdf of NGAD is either a unimodal or a monotonic decreasing function. Further, when we fix other 2 parameters,
![]()
Figure 1. The probability density of NGAD at different parameter values. (a) and (b): β, and η are fixed, and θ values are changed; (c) and (d): θ, and β are fixed, and η values are changed; (e): θ, and η are fixed, and β values are changed.
from Figure 1(a) and Figure 1(b), the shapes tend to be flatten as
decreases and from Figure 1(c) and Figure 1(d), the shapes tend to be flattened as
increases in both cases.
The mode value in the unimodal case can be derived directly from the first derivative of Equation (4), and given as:
Then,
gives the mode value:
and
.
The corresponding cumulative distribution function of NGAD is given by:
(5)
where
.
Note that when
, the NGAD reduces to the AD with parameter
.
3. Statistical Properties
Here, some important statistical properties of the NGAD are derived such as rth moments and related measures, moment generating and characteristic functions, and quantile function.
3.1. Moments and Related Measures
Some basic important characteristics of the distribution such as central tendency, dispersion, skewness, kurtosis, and index of dispersion can be studied by using the moments. The following theorem gives the rth moment about the origin.
Theorem 1. The rth moment about the origin of the NGAD is given by:
(6)
Proof.
The first four moments about the origin are derived by substituting
, and 4 in Equation (6) as:
and
respectively. Then, the rth-order moments about the mean can be obtained by using the relationship between moments about the mean and moments about the origin; i.e.
Therefore,
,
, and
are obtained as:
and
respectively. Then, the the coefficient of variation (c.v), measures of skewness (
), kurtosis (
) and the Index of dispersion/Fano factor (
) of the NGAD can be derived as:
and
respectively. Table 2 shows the skewness and kurtosis values at different parameter value settings. We can observe that for a fixed
or
, skewness and kurtosis show a mixed behaviour while other parameter increases.
3.2. Moment Generating and Characteristic Function
The moment generating function (mgf) and the characteristic function (cf) are directly associated with a probability distribution's characteristics. Further, these can be used to generate the moments of a distribution. The following theorem provides the moment generating function of the NGAD.
Theorem 2. The moment generating function say
of the NGAD is given as follows:
(7)
Proof.
![]()
Table 2. Skewness(Kurtosis) at different values of
and
.
Similarly, the characteristic function say,
of the NGAD can be derived as follows:
(8)
3.3. Quantile Function
The quantile function is useful for quantile estimates and random number generation. The quantile function of NGAD can be derived by solving
. Then, the uth quantile function of NGAD is derived as:
(9)
Equation (9) is not a closed-form. However, the uth quantile can be estimated and random varieties from NGAD can be generated by using the numerical methods.
By substituting
and 0.75 in Equation (9), the first three quartiles can be derived by solving the following equations, respectively.
and
4. Reliability, Inequality and Entropy Measures
In this study, we derive important reliability measures of NGAD such as survival function/reliability function
, hazard rate function/failure rate function
, reversed hazard rate function
, cumulative hazard rate function
, mean residual life function
, and inequality measures, namely Lorenz curve
, and Benferroni curve
. Further, we obtain Renyi entropy measure associated to NGAD.
4.1. Survival and Hazard Rate Functions
The survival function and hazard rate function are crucial functions to specify a survival distribution. The survival function is the probability of surviving up to a point
. Then, the survival function of NGAD is defined as:
(10)
It is clear that,
and
.
The hazard rate function (hrf) is the instantaneous failure rate. It is widely used to describe the lifetime. The hrf of the NGAD is defined as:
(11)
Note that,
and
.
Figure 2 presents the possible shapes of the proposed distribution’s hazard rate function at different shape parameter values. Then, the proposed model has the capability to model the bathtub and monotonic increasing failure rate shapes while the AD has only a monotonic increasing failure rate.
![]()
Figure 2. The hazard rate function of NGAD at different parameter values. (a)
and
are fixed, and
values are changed, (b)
and
are fixed, and
values are changed.
The corresponding reversed hazard rate function of NGAD is defined as:
(12)
and the cumulative hazard rate function of NGAD is defined as:
(13)
4.2. Mean Residual Life Function
The residual life function is defined as the remaining lifetime of a unit of age
until the time of failure. The following theorem derives the mean residual life function of NGAD.
Theorem 3. The mean residual life function of NGAD is given by:
(14)
Proof.
.
Now, consider the integrals separately as follows:
where,
Therefore,
Then, Equation (14) satisfies the following properties
and
4.3. Lorenz and Bonferroni Curves
The Lorenz and Bonferroni curves were formulated to measure the income inequality. They are widely used in economics, reliability, demography, medicine, and insurance. The following theorem derives the Lorenz curve for NGLD.
Theorem 4. The Lorenz curve is defined for FPGLD as
(15)
where,
Proof.
.
Note that
Therefore,
,
and the corresponding Bonferroni curve for the NGAD is defined as:
(16)
where,
and
4.4. Renyi Entropy
The Renyi entropy is a measure of variation of uncertainty measure of a distribution say
[15]. It is an extension of Shannon entropy [16] and widley used in information theory. The following theorem derives the Renyi entropy associated with NGAD.
Theorem 5. The Renyi entropy of the NGAD is given by:
(17)
Proof.
5. The Size-Biased of NGAD
When a recording of observations with an unequal chance, the weighted distributions are used significantly. This provides more flexibility to the standard distributions incorporating sampling probabilities which are proportional to a non-negative weighted function
. The applications of the weighted distributions in reliability, biomedical and ecological sciences have been studied by Patil and Rao (1978) [17]. The weighted random variable
of NGAD is defined as:
(18)
where
.
When
, the resulting distribution is called size-biased version of NGAD with order
, and is defined as:
,
where
is the respective random variable.
The following theorem gives the density function for the sized-biased version of NGAD.
Theorem 6. The density function for rth order sized-biased form of NGAD is derived as:
(19)
where
.
Proof.
.
Note that
Therefore,
By substituting
in Equation (19), the length-biased probability density function can be obtained as:
(20)
6. Parameter Estimation and Inference
In this section, the method of ML is introduced to estimate the parameters of NGAD. Further, the confidence intervals for the unknown parameters are derived.
Let
be identically and independently distributed random variables from NGAD with the likelihood function of the ith sample value
as:
Hence, the log-likelihood function
is given by:
Then, the ML estimators of
, and
, abbreviated as
, and
can be derived by equating the partial derivatives of the l with respect to each parameter to zero. Then, the systems of equations are:
The second partial derivatives of the l are:
By the asymptotic theory, the estimators are asymptotically normal 3-variate with mean (
) and the observed information matrix:
at
, and
. By the asymptotic theory, the estimates are approximately multivariate normal. Therefore, the
confidence interval for the parameters
, and
are given by
wherein, the
, and
are the variance of
, and
, respectively, and can be derived by diagonal elements of
and
is the critical value at a level of significance.
7. Applications
In this section, we examine the performance of the parameter estimates of NGAD by ML method and asymptotic theory respect to sample size n. Here, we perform a simulation study, and further, we illustrate the flexibility of the NGAD over the LD, QLD, TwPLD, LwLD, SD, AD, and ThPLD by using several real data sets.
7.1. Simulation Study
In this subsection, we present the simulation study results to examine the performance of the estimations by the ML method that proposed in Section 6. Equation (9) is used to carry out the simulation study by generating random samples from NGAD, where u is assumed to follow uniform distribution
. The replicates are 1000 in all the simulations with sample sizes 40,100,160, and 220. The combinations of parameter values are set at (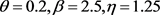 ) to represent the unimodel case and at (
) to represent the unimodel case and at (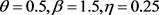 ) to represent the monotonic decreasing case. The average bias and mean square error (MSE) of
) to represent the monotonic decreasing case. The average bias and mean square error (MSE) of  and
and  of the parameters
of the parameters 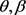 and
and  are computed as follows:
are computed as follows:
1) The average biases are:

2) The average MSEs are:
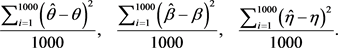
Table 3 summarizes average bias and MSE values of the estimates by the ML method. The average bias values of parameter estimates are considerably small and the corresponding average MSE values decrease when sample size increases. Then, this verifies the asymptotic property of all the estimates.
7.2. Real Data Applications
This subsection is considered to show the flexibility of NGAD over some other existing Lindley family distributions by fitting these to several real data sets. The Akaike Information Criterion (AIC), Bayesian Information Criterion (BIC) and Kolmogorov-Smirnov Statistics (K-S Statistics) are utilized to compare the performance of LD, SD, AD, TwPLD, QLD, LwLD, and ThPLD. The ML method was used to estimate the unknown parameters. The first three real data sets that were considered for the goodness of fit of distributions are given below:
Data set 1: The following data set represents the tensile strength, measured in GPa, of 69 carbon fibres tested under tension at gauge lengths of 20 mm and reported by Bader and Priest (1982) [18].
1.312, 1.314, 1.479, 1.552, 1.700, 1.803, 1.861, 1.865, 1.944, 1.958, 1.966, 1.997, 2.006, 2.021, 2.027, 2.055, 2.063, 2.098, 2.140, 2.179, 2.224, 2.240, 2.253, 2.270, 2.272, 2.274, 2.301, 2.301, 2.359, 2.382, 2.382, 2.426, 2.434, 2.435, 2.478, 2.490, 2.511, 2.514, 2.535, 2.554, 2.566, 2.570, 2.586, 2.629, 2.633, 2.642, 2.648, 2.684, 2.697, 2.726, 2.770, 2.773, 2.800, 2.809, 2.818, 2.821, 2.848, 2.880, 2.954, 3.012, 3.067, 3.084, 3.090, 3.096, 3.128, 3.233, 3.433, 3.585, 3.585.
Data set 2: The following data set reported by Lawless (1982) [1] that arose in tests on endurance of deep groove ball bearing. The data are the number of million revolutions before failure for each of the 23 ball bearing in the life tests.
17.88, 28.92, 33, 41.52, 42.12, 45.6, 48.8, 51.84, 51.96, 54.12, 55.56, 67.8, 68.44, 68.64, 68.88, 84.12, 93.12, 98.64, 105.12, 105.84, 127.92, 128.04, 173.4.
Data set 3: The following data set represents the tree circumferences in Marshall, Minnesota and reported by Shakil, Kibria, and Singh (2010) [19].
1.8, 1.8, 1.9, 2.4, 3.1, 3.4, 3.7, 3.7, 3.8, 3.9, 4.0, 4.1, 4.9, 5.1, 5.1, 5.2, 5.3, 5.5, 8.3, 13.7.
Some of the statistical measures for data set 1, 2 and 3 are given in Table 4.
The fitted density plot of each distribution is shown in Figure 3 for data set 1, 2, and 3 separately. Each fitted density compares with the empirical histogram of the real data sets. Here, we may observe that the fitted density for the NGAD shows a closer fit with the empirical distributions. The AIC, BIC, and K-S statistics with critical values for NGAD, LwLD, TwPLD, QLD, ThPLD, AD, LD, and SD are shown in TableS1 (Appendix). Based on minimum AIC, BIC values and significant results by K-S statistics, the NGAD provides a better fit than all other distributions for light-tailed distributions (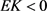 ) as well as heavy-tailed distributions (
) as well as heavy-tailed distributions ( ). Further, it is noted that the LwLD performs better than NGAD for the data set with a considerably high positive EK value.
). Further, it is noted that the LwLD performs better than NGAD for the data set with a considerably high positive EK value.
Then, similarly we have fitted NGAD and LwLD to several real-data sets (Appendix) having different EK values and compare their performances. Table 5 summarizes the results of the goodness of fit test for these data sets. It is clear that NGAD may perform better than LwLD for considerably small EK values.
![]()
Table 3. Simulation results for average bias and MSE values of NGAD.
![]()
Table 4. Statistical measures for data set 1, 2, and 3.
![]()
Table 5. AICs, and K-S statistics of the NGAD and LwLD for different data sets with various EK values.
![]()
Figure 3. Empirical histograms with fitted densities of distributions.
8. Conclusion
In this study, a new generalized Akash distribution has been introduced by incorporating the location parameter to improve the flexibility of the failure rate function. Then, its structural properties including parameter estimation have been discussed. This new distribution yields a more flexible density and failure rate shapes. Further, it has the capability to model the bathtub and monotonic increasing failure rate shapes. The simulation study indicates that the ML method performs well in the estimation of the unknown parameters for NGAD. To illustrate the theoretical findings, the real-world applications were used, and the results reveal that the NGAD is superior over AD, Lindley distribution (LD) and some other existing modified LDs that have been developed based on exponential and gamma mixtures with different mixing proportions. Based on the special characteristics, the proposed model may attract wider applications in reliability, mortality, actuarial, ecological sciences, among others.
Acknowledgements
We thank the Postgraduate Institute of Science, University of Peradeniya, Sri Lanka for providing all facilities to do this research.
Appendix
Data Sets
Data set 4 (Mol.et al., (2012)): the data represents the level of mercury [20].
1.007, 1.447, 0.763, 2.010, 1.346, 1.243, 1.586, 0.821, 1.735, 1.396, 1.109, 0.993,2.007, 1.373, 2.242, 1.647, 1.350, 0.948, 1.501, 1.907, 1.952, 0.996, 1.433, 0.866, 1.049, 1.665,2.139, 0.534, 1.027, 1.678, 1.214, 0.905, 1.525, 0.763.
Data set 5 (Fuller.et al., (1994): the data represents the strength of glass of the aircraft window [21].
18.83, 20.80, 21.657, 23.03, 23.23, 24.05, 24.321, 25.50, 25.52, 25.80, 26.69, 26.77, 26.78, 27.05, 27.67, 29.90, 31.11, 33.20, 33.73, 33.76, 33.89, 34.76, 35.75, 35.91,36.98, 37.08, 37.09, 39.58, 44.045, 45.29, 45.381.
Data set 6 (Nichols.et al., (2006): the data are breaking stress of carbon fibers [22].
3.70, 2.74, 2.73, 2.50, 3.60, 3.11, 3.27, 2.87, 1.47, 3.11, 3.56,4.42, 2.41, 3.19, 3.22, 1.69, 3.28, 3.09, 1.87, 3.15, 4.90, 1.57, 2.67, 2.93, 3.22, 3.39, 2.81, 4.20, 3.33, 2.55, 3.31, 3.31, 2.85,1.25, 4.38, 1.84, 0.39, 3.68, 2.48, 0.85, 1.61, 2.79, 4.70, 2.03,1.89, 2.88, 2.82, 2.05, 3.65, 3.75, 2.43, 2.95, 2.97, 3.39, 2.96, 2.35, 2.55, 2.59, 2.03, 1.61, 2.12, 3.15, 1.08, 2.56, 1.80, 2.53.
Data set 7 (Smith.et al., (1987): the data represents the strength of glass fibers [23].
0.55, 0.93, 1.25, 1.36, 1.49, 1.52, 1.58, 1.61, 1.64, 1.68, 1.73, 1.81, 2, 0.74, 1.04, 1.27, 1.39, 1.49, 1.53, 1.59, 1.61, 1.66, 1.68, 1.76,1.82, 2.01, 0.77, 1.11, 1.28, 1.42, 1.5, 1.54, 1.6, 1.62, 1.66, 1.69,1.76, 1.84, 2.24, 0.81, 1.13, 1.29, 1.48, 1.5, 1.55, 1.61, 1.62, 1.66,1.7, 1.77, 1.84, 0.84, 1.24, 1.3, 1.48, 1.51, 1.55, 1.61, 1.63, 1.67,1.7, 1.78, 1.89.
Data set 8 (Birnbaum.et al., (1969)): the data are fatigue life of 6061T6 aluminum coupons [24].
70, 90, 96, 97, 99, 100, 103, 104, 104,105, 107, 108, 108, 108, 109, 109, 112, 112, 113, 114, 114, 114, 116, 119, 120,120, 120, 121, 121, 123, 124, 124, 124, 124, 124, 128, 128, 129, 129, 130, 130,130, 131, 131, 131, 131, 131, 132, 132, 132, 133, 134, 134, 134, 134, 136, 136,137, 138, 138, 138, 139, 139, 141, 141, 142, 142, 142, 142, 142, 142, 144, 144,145, 146, 148, 148, 149, 151, 151, 152, 155, 156, 157, 157, 157, 157, 158, 159,162, 163, 163, 164, 166, 166, 168, 170, 174, 201, 212.
Data set 9 (Weisberg, (2005): the data are athletes’ skin folds [25].
28.0, 109.1, 102.8, 104.6, 126.4, 80.3, 75.2, 87.2, 97.9, 75.1, 65.1, 171.1,76.8, 117.8, 90.2, 97.2, 99.9, 125.9, 69.9, 98, 96.8, 80.3, 74.9, 83.0, 91.0, 76.2, 52.6, 111.1,110.7, 74.7, 113.5, 99.8, 80.3, 109.5, 123.6, 91.2, 49.0, 110.2, 89.0, 98.3, 122.1, 90.4, 106.9,156.6, 101.1, 126.4, 114.0, 70.0, 77.0, 148.9, 80.1, 156.6, 115.9, 181.7, 71.6, 143.5, 200.8, 68.9,103.6, 71.3, 54.6, 88.2, 95.4, 47.5, 55.6, 62.9, 52.5, 62.6, 49.9, 57.9, 109.6, 98.5, 136.3, 103.6,102.8, 131.9, 33.8, 43.5, 46.2, 73.9, 36.8, 67, 41.1, 59.4, 48.4, 50.0, 54.6, 42.3, 46.1, 46.3, 109.0,98.1, 80.6, 68.3, 47.6, 61.9, 38.2, 43.5, 56.8, 41.6, 58.9, 44.5, 41.8, 33.7, 50.9, 40.5, 51.2, 54.4,52.3, 57.0, 65.3, 52.0, 42.7, 35.2, 49.2, 61.8, 46.5, 34.8, 60.2, 48.1, 44.5, 54.0, 44.7, 64.9, 43.8,58.3, 52.8, 43.1, 78.0, 40.8, 41.5, 50.9, 49.6, 88.9, 48.3, 61.8, 43.0, 61.1, 43.8, 54.2, 41.8, 34.1,30.5, 34.0, 46.7, 71.1, 65.9, 34.3, 34.6, 31.8, 34.5, 31.0, 32.6, 31.5, 32.6, 31.0, 33.7, 30.3, 38.0,55.7, 37.5, 112.5, 82.7, 29.7, 38.9, 44.8, 30.9, 44.0, 37.5, 37.6, 31.7, 36.6, 48, 41.9, 30.9, 52.8,43.2, 113.5, 96.9, 49.3, 42.3, 96.3, 56.5, 105.7, 100.7, 56.8, 75.9, 52.8, 47.8, 76.0, 61.2, 75.6,43.3, 49.5, 70.0, 75.7, 57.7, 67.2, 56.5, 47.6, 60.4, 34.9.
Data set 10 (Bjerkedal, (1960)): the data represents he survival times of guinea pigs [26].
0.1, 0.33, 0.44, 0.56, 0.59, 0.72, 0.74, 0.77, 0.92, 0.93, 0.96, 1, 1, 1.02, 1.05, 1.07, 1.07, 1.08, 1.08, 1.08, 1.09, 1.12, 1.13, 1.15, 1.16, 1.2, 1.21, 1.22, 1.22, 1.24, 1.3, 1.34, 1.36, 1.39, 1.44, 1.46, 1.53, 1.59, 1.6, 1.63, 1.63, 1.68, 1.71, 1.72, 1.76, 1.83, 1.95, 1.96, 1.97, 2.02, 2.13, 2.15, 2.16, 2.22, 2.3, 2.31, 2.4, 2.45, 2.51, 2.53, 2.54, 2.54, 2.78, 2.93, 3.27, 3.42, 3.47, 3.61, 4.02, 4.32, 4.58, 5.55.
Data set 11 (Mead, (2016)): the data consist the taxes revenue [27].
5.9, 20.4, 14.9, 16.2, 17.2, 7.8, 6.1, 9.2, 10.2, 9.6, 13.3, 8.5, 21.6, 18.5,5.1,6.7, 17, 8.6, 9.7, 39.2, 35.7, 15.7, 9.7, 10, 4.1, 36, 8.5, 8, 9.2, 26.2,21.9,16.7, 21.3, 35.4, 14.3, 8.5, 10.6, 19.1, 20.5, 7.1, 7.7, 18.1, 16.5, 11.9, 7,8.6,12.5, 10.3, 11.2, 6.1, 8.4, 11, 11.6, 11.9, 5.2, 6.8, 8.9, 7.1, 10.8.
Data set 12 (Choulakian.et al., (2001): the data are flood peaks [28].
1.7, 2.2, 14.4, 1.1,0.4, 20.6, 5.3,0.7, 1.9,13.0, 12.0, 9.3, 1.4, 18.7, 8.5,25.5, 11.6, 14.1, 22.1, 1.1, 2.5, 27.0, 14.4, 1.7, 37.6, 0.6,2.2,39.0, 0.3,15.0, 11.0, 7.3, 22.9, 1.7, 0.1, 1.1, 0.6, 9.0, 1.7, 7.0, 20.1, 0.4, 2.8, 14.1, 9.9, 10.4, 10.7, 30.0, 3.6, 5.6, 30.8, 13.3, 4.2, 25.5, 3.4,11.9, 21.5, 27.6, 36.4, 2.7, 64.0,1.5,2.5,27.4, 1.0,27.1, 20.2, 16.8, 5.3,9.7,27.5, 2.5.
Data set 13 (Gross.et al., (1975)): the data represent the relief times of patients [29].
1.1, 1.4, 1.3, 1.7, 1.9, 1.8, 1.6, 2.2, 1.7, 2.7, 4.1, 1.8, 1.5, 1.2, 1.4, 3.0, 1.7, 2.3, 1.6, 2.0.
![]()
![]()
Table S1. MLEs, AIC, BIC, K-S statistics and its critical value of the fitted distributions.