Comparative Appraisal of Response Surface Methodology and Artificial Neural Network Method for Stabilized Turbulent Confined Jet Diffusion Flames Using Bluff-Body Burners ()
1. Introduction
Bluff-body stabilized turbulent gaseous jet diffusion flames have received renewed attention in recent years due to its practical applications such as, gas burners of industrial furnaces, gas turbine combustion chamber, ramjets and flaring of petroleum industry.
The practical importance of the bluff-body stabilization process has raised a large number of theoretical and experimental studies over the years to identify the physical mechanisms for the stability limits at different geometries of bluff-body acting as flame holders. Several pioneering works have proposed overall flow field classifications based on the observed flame structure as follows:
The effects of bluff-body lip thickness on physical parameters like flame length, radiant fraction, gas temperature and NOx emissions in (LPG-H2) jet diffusion flame were investigated experimentally [1]. The results indicated that the flame length reduces with addition of hydrogen in the bluff-body stabilized flame, which can be attributed to the enhanced reactivity of the mixture gases. Moreover the flame length was reduced, flame temperature was increased and NOx emission level was enhanced with increasing lip thickness of the bluff-body. Also, Mishra and Kiran [2] presented another experimental study to investigate the effect of coaxial air velocity and lip thickness of the bluff-body on the stability limits of LPG diffusion flames. The flame stability was found to be improved for larger lip-thickness bluff-body because of the presence of lower pressure in the wake behind the bluff-body.
The effect of flame holder geometry on flame structure in non-premixed combustion was studied [3]. The investigation showed that increasing in flame holder length decreases flame length and increases flame temperature. Also, it was found that flame lengths decrease by increasing in flame holder radius and increase for larger radii. In addition, the attained numerical results employing realizable k-ε and β-PDF models display a good agreement with the experimental data. Furthermore, the effect of the flame holder geometry on flame structure of a mixed hydrogen-hydrocarbon fuel was numerically studied [4]. Numerical results obtained by means of the K-ε and β-PDF models demonstrate good agreement with experimental data. The results revealed that increasing both the flame holder length and hydrogen percentage in the fuel decreases the flame length. Also, the flame temperature decreases with decreasing flame holder length.
Furthermore, the turbulent non-premixed flames of natural gas/air stabilized in a semi-infinite bluff-body burner were assessed at different situations corresponding either to jet or to wake-dominated to the base of flow field structure. The aim was to identify the influence of the fuel jet and air co-flow velocities on the measured results at the flame stabilization region in situations where intermittent flame lift off and partial extinction may occur [5].
Recently, Yiheng Tong, et al. [6] designed a burner which has a conical bluff-body with a central air injector. This investigation revealed the effects of the central air jet on reducing the heat load of the bluff-body which is considered a solution to this problem in practical applications. Flame structures and flame stability limits were observed and reported due to the enhanced mixing characteristics in the presence of the bluff body in the combustion domain. Also, numerical investigation on combustion characteristics of methane/air flames in a micro-combustor with a regular triangular pyramid bluff-body was reported [7]. Their results revealed that the blow-out limit of the micro combustor with the triangular pyramid bluff-body was 2.4 times that in the micro-combustor without bluff-body. Also, it was found that the methane conversion rate and the temperature behind bluff-body reach the highest where blockage ratio increases to 0.22.
Another work of the non-reacting flow field and the mixing characteristics of an axisymmetric bluff-body disc burner had been investigated under inlet mixture stratification and preheat [8]. The burner consists of three concentric disks that form two premixing cavities. The study had been performed to evaluate the flow fields developing in the downstream near wake. The study had helped to elucidate the effects of inlet mixture stratification, alone or with preheat in the presence of the disc stabilizer and to identify parameters that control the mixture in the recirculation zone.
More recently, the experimental work investigated by [9] discussed the characteristics of isothermal flow and scalar mixing fields, downstream of a variety of axisymmetric baffles in a double-cavity disc burner configuration. The aim of this work was to enhance the knowledge of the effect of inlet fuel-air mixture conditions and the geometric parameters of blockage ratios in the near recirculating wake of the practical flame stabilizers. The findings can be appropriately exploited for the regulation of inlet mixture profile variations and the minimization of emissions in the development of combustors.
2. Modeling
Modeling is a scientific approach and essential part of many scientific disciplines to represent ideas about the natural of the phenomenon under investigation from the viewpoint of science and to present an alternative to the real phenomenon, to quantify, define, visualize, or simulate it by referring to the existing knowledge. There are several types of modeling approaches, among which the most widely used are mathematical and intelligent modeling approaches [10].
In industry, the most advanced processes require accurate models if high performance is to be attained as they are nonlinear in nature, which makes developing precise models challenging. When investigating the precision of the modeling technique, various factors, ranging from the nonlinearity of the model behavior to the dimensionality and data sampling technique, to the internal parameters, are noticeably affected. The need for a model that can accurately predict experimental behavior has been the utmost challenge for researchers over the years; such models can dramatically reduce the time and operational cost in many engineering aspects. From here emerged the need to model processes [11].
Artificial neural networks (ANNs) and response surface methodology (RSM) are important approaches in the field of processes modeling and optimization. These methods of modeling estimate the relations between the output (response or target variable) and input variables (experimental operating factors) of the process by means of experimentally derived data. Subsequently, derived models are used to approximate the optimum situations of independent variables to minimize or maximize the target variable (dependent variable) [12].
RSM is an effective technique, which enables the estimation of desired response from a number of independent variables as well as the interactions between them. The key advantage in RSM is that fewer experimental runs are sufficient to provide a statistically significant result. Besides analyzing individual variables, it can also generate a mathematical model for the process to determine the optimum condition of a process and to investigate the influencing factors. Despite its simplicity and efficiency, RSM provides efficient and accurate solutions. Therefore, it has successfully been applied in many engineering problems [11] [13].
ANN modeling is a relatively new nonlinear statistical technique developed to solve problems that are not eligible for conventional statistical methods. It is a factual computing technique developed based on comportment of the biological neural system. It can handle obscure, complex, incomplete problem and execute modeling to produce predictions and generalizations at high speed. Both RSM and ANN techniques do not need the precise expressions or the physical meaning of the system under investigation [13].
Ahmadpour et al. [12] in their investigation of spent caustic wastewater treatment through RSM and ANN in a photocatalytic reactor evidenced from the obtained results that the ANN model showed higher accuracy than the response surface model did.
Awolusi et al. [14] stated that the comparison between ANN and some classical modeling techniques such as response surface methodology (RSM), showed the supremacy of ANN as a modeling technique in analyzing non-linear relationships of data sets, which consequently provides good fitting for data and as well as better predictive ability.
Karkalos et al. [15] in the comparative study between regression and neural networks for modeling Al6082-T6 alloy drilling found that the MLP_ANN models were superior to the regression model, as they were able to achieve a relatively lower prediction error.
Manda et al. [16] in their approach to predict the effects of formulation and process variables on prednisone release from a multipartite System proved that ANN has better modeling accuracy than RSM.
RSM and ANN were studied and compared for modeling highly nonlinear responses found in impact-related problems. Despite the computation cost of ANN, these studies concluded the supremacy of ANN over RSM in such optimization problems [11].
The present study focuses on the evaluation of the predictive capabilities of the RSM and ANN two methodologies for the previously reported experimental data of thermal structure of the stabilized flames in the presence of different geometries of bluff-body burners [17]. This has been performed by comparing the values of coefficient of determination (R2), F_Ratio and the various error analyses parameters. Moreover ANN method has been exploited to illustrate the effect of input flame parameters on the response in three and two dimensions and to display the location of the optimum.
3. Response Surface Methodology
The Response Surface Methodology (RSM) was introduced, developed and used in many studies based on polynomial functions in the 1980s. In the last decade, RSM has been extensively utilized for modeling and optimization of several engineering processes and studies. This methodology is an assortment of statistical techniques for the experimental design, the building of the models, evaluating the consequences of factors, and searching for the optimum conditions [18]. This technique is one of the major quantitative tools in industrial decision making as it gives better understanding of the process; it helps the process engineer to see the effect of the control variables simultaneously and the interactions among all the variables [19]. It generates a mathematical model; its graphical perspective has led to the term Response Surface Methodology [20]. These graphic drawings of the shape of the surfaces allow a visual explanation of the functional relations between the response and the experimental variables [21] [22]. RSM also permits the location of the optimum conditions and sensitivity analyses of the optimum conditions to variations in the settings of the experimental variables. This technique has many advantages such as: cost and time reduction, decreasing the number of tests and valuable in attaining maximum efficiency [23]. However it is associated with the following shortcomings: increased number of variables significantly decreases the accuracy of this method and increased number of variables is very time-consuming for analysis [24]. Moreover RSM based models are exact for only a limited range of input process parameters, and thus, impose a limitation on the use of RSM models for highly non-linear processes [25].
RSM can be divided into the following steps: 1) selection of the independent variables and responses, 2) selection of the experimental design, 3) execution of experiments and collection of results, 4) mathematical modeling of experimental data by polynomial equations, with the best fitting response, 5) checking of models through analysis of variance, 6) drawing of response surfaces, 7) evaluating main and interactional effect of variables using 2D or 3D plots, and, finally, 8) identification of optimal conditions [16] [26] [27].
The units of the natural independent variables vary from one another. Even if some of the parameters have the same units, not all of these parameters will be tested over the same range. Before performing the regression analysis the variables should be codified to eliminate the effect of different units and ranges in the experimental domain and allows parameters of different magnitude to be investigated more evenly in a range between −1 and +1 [20] [28] [29].
The frequently used equation for coding is seen below:
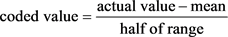(1)
Functional relationships between the coded independent variables and dependent variables have been established using multiple regression technique by fitting second order equation of the following form [18] :
(2)
Details of this method have been dealt with in our previous papers [30] [31] [32].
4. Artificial Neural Networks
ANNs were introduced as universal function approximators by McCulloch and Pitts in 1943 [33] and have been extensively used in many areas ever since as a powerful and reliable tool serving data mining and numerical applications because of its powerful control over regulatory parameters for pattern recognition and classification. NN is a computational mechanism that is able to acquire, represent, and compute a mapping from multivariate space of information to another, given a set of data representing that mapping. ANNs are designed to simulate the human brain when analyzing data by learning from experience. Similar to the human brain, ANNs are capable of processing multi-dimensional, non-linear, clustered and imprecise information and could be used to extract a pattern in nonlinear, complex and noisy data sets to detect the trends with high accuracy. Thus, ANN can be used to decode complicated real world problems that are sometimes challenging to evaluate using statistical approaches without the need for complicated equations, and is capable of exploring regions that are otherwise omitted when using statistical approaches [14] [16] [24] [25] [27] and [34]. They are widely used by researchers to solve a variety of problems in science and engineering, forecasting, multivariate data analysis using experimental data, field observations or even incomplete or fuzzy data sets particularly for some areas where the conventional modeling methods fail such as prediction of internal combustion engine performance characteristics [35]. The key privilege of ANN-model is that it is not necessary to specify a preceding proper fitting function; so, it has a complete calculation capability to estimate practically all types of nonlinear functions which helps us to develop the most accurate prediction model [11] [36]. The prediction by a well-trained ANN is normally much faster than the conventional simulation programs or mathematical models as no lengthy iterative calculations are needed to solve differential equations using numerical methods but the selection of an appropriate neural network topology is important in terms of model accuracy and model simplicity [35].
ANN is a colossal structure of interconnected networks based on a simplified analogy to the behavior of the human brain consisting of numerous individual elements called neurons, which are mathematically represented by relatively simple yet flexible functions, such as linear or sigmoid functions capable of performing parallel computations for data processing. These processing units communicate with each other by means of weighted connections, corresponding to the synapses of the brain [18] [37]. Different networks can be constructed by choosing different numbers of neuron layers, the type and number of neurons in each layer, and the type of connection between neurons. For a specific configuration of the network and for a given set of input-output data, the so-called training of the network consists of adjusting its parameters in order for the network to reproduce the input-output data as accurately as possible. Each iteration of the training process is called an epoch and composed of forward activation to produce a solution and the backward propagation of the calculated error to adjust the weights [35] [37] and [38].
The advantages of ANN are as follows: distributed information processing and the inherent potential for parallel computation. In many cases, when sufficiently rich data are available, they can provide fairly accurate models for nonlinear controls when model equations are not known or only partial state information is available. Due to their parallel processing capability, nonlinearity in nature and their ability to model without a priori knowledge, ANN can be used successfully to capture the dynamics of multivariable nonlinear systems [39].
5. Neuron Model
An elementary neuron with R inputs is shown below, Figure 1(a). Each input is weighted with an appropriate w. The sum of the weighted inputs and the bias forms the input to the transfer function f. Figure 1(b) depicts the tansig differentiable transfer function f to generate the output between −1 and 1 as the neuron’s net input goes from negative to positive infinity. Figure 1(c) shows the linear transfer function purelin. These transfer functions described here are the most commonly used transfer functions for multilayer networks [40].
6. Feed Forward Neural Network
The multi-layer perceptron (MLP), also called feed-forward back propagation network is the most widely used network type for approximation problems. Feed forward networks often have one or more hidden layers of sigmoid neurons followed by an output layer of linear neurons besides an input layer. Figure 2 portrays two-layer tansig/purelin network. Multiple layers of neurons with nonlinear transfer functions allow the network to learn nonlinear relationships between input and output vectors. The linear output layer is most often used for function fitting (or nonlinear regression) problems [40].
![]()
Figure 1. (a) Elementary neuron; (b) Tansig transfer function; (c) Purelin transfer function.
The number of input neurons represents and is equal to the independent variables of the system and the number of output neurons represents and is equal to the response of the system. Each input unit is attached to all hidden units and each hidden unit is attached to the output layer and there is no communication between neurons in the same layer [41].
The neurons of one layer are connected with each neuron of the previous and next layer, but information only flows in the forward direction, from the input towards the output layer [37]. For approximation of functions with minor discontinuities generally a combination of layers with sigmoid activation functions and a linear output layer is used. Linear activation functions are used for the input (where input values are simply passed onto the neurons in the next layer) and output layers, and tangent-sigmoid neurons are chosen for the hidden layer. In the passage, each value is multiplied by the respective weight, which characterizes the connection between neurons of the layers; hence a weighted sum is passed to the hidden layer neurons. A bias factor is added to the weighted sum, which allows, for instance, an activation of the neuron even when a null value is passed to it. In the hidden layer, input values are processed by the activation function of each neuron, returning a value between −1 and +1 in the case of the tangent sigmoid function. The resulting values are transmitted to the output layer. The output neurons add their own biases to the weighted sum they receive and return the network response for the input data provided to the network. The weights which characterize the connection between the neurons and the bias of each neuron are the network parameters to be determined during the training process [37].
The input variables should also be codified in case of ANN as the normalization leads to avoidance of numerical over flows due to very large or very small weights and to prevent mismatch between the influence of some input values to the network weights and biases [42] beside preventing problems such as reduced accuracy and network instabilities in the course of training process [43]. The output values obtained from the ANN are also in the range of −1 to 1, and converted to their original data based on the reverse method of normalization [25].
In training of the back propagation method, the error is determined by comparing the output and the desired output and this error is returned to the hidden and input layers of the next training processes. The network training operation ends when the error comes down below some value specified by the user [10].
The input-output data is separated into three groups: training, validation and test data. The first group is the only one used to generate the model structure for adjustment of the parameters; validation is used between epochs to optimally select model parameters, in order to halt the training process if the network error starts to increase due to over fitting; and the test data is used to verify the networks predicting capacity at the end of training [37] [43].
The MATLAB neural network toolbox has been employed for generating, training and using the ANNs. The training is performed employing the Levenberg–Marquardt (LM) due to its fast convergence and reliability in locating the global minimum of the mean-squared error (MSE) [42]. LM is hybrid of the Gauss Newton nonlinear regression method and gradient steepest descent method based on the least squares method for nonlinear models employing the Jacobian matrix [37] [40] and [43].
Mathematical equation relating the input/output variables is given by using the following equation [27].
(3)
where: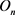 
is the normalized output ranging from −1 to 1; 
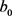is the output bias; 
is the connection weight between kth neuron of hidden layer and the single output neuron;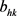 
is the bias at the kth neuron of hidden layer; h is the number of neurons in the hidden layer; 
is the connection weight between ith input variable and kth neuron of hidden layer; 
is the normalized input variable i in the range [−1, 1]; 
is the sigmoid transfer function & 
is the linear transfer function.
The Levenberg-Marquardt algorithm uses the following updating function
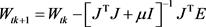(4)
where:
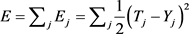(5)
J is the Jacobian matrix, which contains first derivatives of the network errors with respect to the weights and biases parameters of the ANN. I is the identity matrix, E is a vector of network errors, W contains both the weights and biases of the ANN, μ is a scalar, a parameter of the algorithm, and tk represents the current training epoch [37]. ![]()
is the output value of the jth output neuron and ![]()
is the desired value of the jth output neuron. The ![]()
sigmoid transfer function is defined by the following relation [40] :
![]()
(6)
To obtain an ANN the following steps must be completed: a) selection of data for learning, b) network architecture selection, c) determination of weight and threshold values, d) verification and validation of the prediction model on the basis of error function, and, optionally, e) optimization of the function learned by ANN [26].
7. Application of RSM and ANN to the Present Work
· Experimental
Details of the experimental setup and the data employed in this study have been given the previous work of [17] [44].
The coded factors of (r) and ![]()
have been calculated employing the following formulas:
![]()
(7)
where:
r: radial distance from the center line of the flame (mm);
X: axial distance along the flame over the disc (mm);
![]()
: jet diameter (mm).
8. ANN Modeling Process
The development process of our MLP network was performed using the Artificial Neural Network Toolbox in MATLAB (R2016a, Math Works, Natick, MA, USA).
We built a three-layer feed-forward ANN with two input neurons representing the coded influencing factors; one output neurons representing the dependent response variable. The back propagation algorithm has been applied to obtain the best fit to the training data because of its capacity of representing non-linear functional relationships between inputs and targets. As activation functions, we used the hyperbolic tangent sigmoid (tansig) for the hidden layer and linear (purelin) for the output layer. The Levenberg-Marquardt back-propagation training algorithm was used for minimizing the error function of the ANN. The mean square error (MSE) was used as performance function.
In the first step, the imported processing data matrix from laboratory experiment results included the coded X and R as input variables and radial mean temperature as an output variable. In the second step, the imported data were randomly divided by the network into three categories of training data (with a share of 70%), test data (with a share of 15%) and validation data (with a share of 15%). In order to identify the optimum network architecture, it is essential to determine the number of neurons in the hidden layer. Therefore, the number of neurons was chosen from 3 to 14 neurons in the hidden layer and the performance parameter (MSE) of each run was accordingly calculated with respect to the target value. The network with 10 neurons in hidden layer shows the best results of minimum MSE. For a certain group of neurons in the hidden layer different results may be obtained in each training process. In each network training process, the weight and bias were corrected to reduce the tilt of the performance function and the output matrix of the network. Therefore, training process for each number of neurons in the hidden layer was executed in five repetitions while the value of the performance function was calculated for each repetition and the average value of the performance function for five repetitions was obtained. Calculating the average value eliminates the effect of the output differences [10].
9. Models Validation and Evaluation
In order to evaluate the goodness of the model fitting and prediction accuracy of the constructed models, R2, F_ratio and error analyses were performed between the experimental and predicted data in the RSM, and ANN models. Many approaches for error analyses are stated in the literature, with some listed in a previous study [11] [45]. The formulas employed in this study for performance evaluation and error analyses are listed in Tables 1(a)-(c).
(a) ![]()
(b) ![]()
(c) ![]()
Table 1. (a) Performance and Error functions and their equations; (b) Performance and Error functions and their equations; (c) Performance and Error functions and their equations.
where: n: is the number of experimental data points;![]()
: is the experimental value of the ith data point;![]()
: is the corresponding value of the ith experimental data point predicted by the model;![]()
: is value of the average experimentally measured temperatures and ![]()
is value of the average predicted temperatures. ![]()
and ![]()
denote the ith and the average value of the ith input variable respectively (k = R and X). ![]()
and ![]()
refer to the ith predicted temperature and average predicted temperature respectively.
For the RSM several mathematical models have been suggested to establish the relationship between the dependent and independent variables. The Box-Cox method has been utilized to identify a suitable power transformation to the response data for normalizing the data or equalizing its variance. The following transformations; of the mean temperature T dependent variable; sqrt(T), Ln(T) and (T) have been resulted and employed for D30, D60 and DFC respectively to represent the response Y in Equation (2) [31].
In the present study the following cases have been considered for D30, D60 & DFC:
Case a—For all discs, the response temperature has been employed as it is for Y in Equation (2) and for training in case of ANN and the predicted temperatures were compared with the corresponding experimental temperature ones.
For D30 the following trials have been performed:
Case b—The sqrt(T) has been employed in Equation (2) as Y and for training in case of ANN and the predicted results in both cases have been converted to the equivalent predicted temperature to be compared with the corresponding experimental temperature ones.
Case c—The sqrt(T) has been employed in Equation (2) as Y and for training in case of ANN and predicted results in both cases have been compared with the corresponding sqrt(experimental temperature) ones.
For D60 the following trials have been performed:
Case b—The ln(T) has been employed in Equation (2) as Y and for training in case of ANN and the predicted results in both cases have been converted to the analogous predicted temperature to be compared with the corresponding experimental temperature ones.
Case c—The Ln(T) has been employed in Equation (2) as Y and for training in case of ANN and the predicted results in both cases have been compared with the corresponding Ln(experimental temperature) ones.
10. Results and Discussions
The results of comparison are presented in Tables 2(a)-(c). These results exposed that the properly trained ANN model has consistently performed more accurate prediction closer to experimentally measured ones compared to RSM model in all aspects hinting that ANN model was quite successful for both simulation and predicted values. Similar observations were obtained by many research groups to study various engineering problems [25]. This is expressed in the very high values of R2 & F ratio and the extremely low value of error indicators for the ANN results compared to that of RSM ones. This is more pronounced by comparing the results of the studied case a for the values of R2 (0.98312, 0.9683, 0.98745 in case of ANN compared to 0.9231, 0.86814, 0.93575 in case of RSM) and of F ratio (5658.57, 2922.47, 7580.67 in case of ANN compared to 540.154, 231.747, 864.077 in case of RSM) for D30, D60 & DFC respectively. Moreover the ranges of R2, F_Ratio in all the studied cases are 0.868 -
(a) ![]()
(b) ![]()
(c) ![]()
Table 2. (a) Performance and Evaluation of RSM and ANN methods; (b) Performance and Error evaluation for RSM and ANN; (c) Performance and Error evaluation for RSM and ANN.
0.947 & 231.7 - 864.1 for RSM method compared to 0.964 - 0.987 & 2878.8 7580.7 for ANN method. The better modeling ability of ANN can be attributed to its universal approximation ability for nonlinearity, whereas RSM is only limited to a second-order polynomial regression [46].
Also the predicted temperatures in all the studied cases were compared with corresponding experimental ones and the error was referred to the maximum experimental temperature and this comparison is displayed in Table 2(a) as ![]()
calculated by the following Equation (8). In all cases studied for the three discs the ![]()
for the ANN method was less than that for the RSM method.
![]()
(8)
These results indicate that the ANN model shows a significantly excellent generalization capacity than the RSM models. This can be attributed to the universal ability of ANN to approximate the nonlinearity of the system, whereas the RSM is restricted to a second-order polynomial.
Table2(a) presents RF values for each parameter. This Tableindicates the positive relevancy factor of ![]()
which means that the temperature increases with the increasing of![]()
, while the radius has a very small relevancy factor indicating the trivial effect of radius on the measured temperature.
Also, this table discloses that the ANN method is more expensive than RSM indicated in the larger elapsed time for NN compared to that of RSM, because it uses a series of computationally expensive functions for a single model.
The three-dimensional concave curved response surfaces in Figures 3(a)-(c) indicate the possibility of obtaining a maximum value of the measured temperature within the chosen factors levels and the interaction between the factors [38].
The contour plots of Figures 4(a)-(c) assess the individual and cumulative influence of the variables and the mutual interaction between the variables and the dependent variable [47] [48]. The oval shape of the contour plots indicates a significant interaction between the independent variables. The smallest ellipses in the contour plots represent the maximum predicted values [46].
11. Comparative Evaluation of RSM and ANN
Modeling using RSM is easier compared to ANN, as ANN needs a higher number of inputs than RSM for better predictions. ANN has excellent prediction and optimization abilities, while sensitivity analysis is more precise in RSM. RSM is recommended for modeling of a new process, while ANN is best suited for nonlinear systems that include interactions higher than quadratic. Moreover ANN does not require any prior specification for suitable fitting function [46].
The structured nature of RSM provides the predicted quadratic equation to exhibit the factors contributions from the coefficient regression of the models.
![]()
(a) ![]()
(b) ![]()
(c)
Figure 3. (a) Surface plot for D30 using ANN; (b) Surface plot for D60 using ANN; (c) Surface plot for DFC using ANN.
![]()
(a) ![]()
(b) ![]()
(c)
Figure 4. (a) Contour plot for D30 using ANN; (b) Contour plot for D60 using ANN; (c) Contour plot for DFC using ANN.
This ability is robust in identifying the significant and insignificant terms in the model and hence can reduce the complexity of the models. However, the ANN presents a better alternative in modeling and prediction [49]. The Artificial Neural Network (ANN) model provides little information about the influencing factors and their contribution to the response if further analysis has not been done [50].
The higher predictive accuracy of the ANN is attributed to its ability to process multi-dimensional, non-linear and clustered information whereas RSM is limited to use of a second order polynomial. The generation of an optimum ANN is a multi-step calculation process, that is repeated until a desirable error is achieved whereas a response surface model is based on a single step calculation [16] [50].
12. Simulation and Optimization
Since it had been established that the neural network was able to efficiently predict the temperature for the various conditions of the experiments, the final network with the optimum NN architecture was utilized for the optimization purpose for the above three mentioned cases for the three discs. The optimization was executed by a grid search algorithm, exploring the region defined by two of the coded experimental input variables design limits and dividing each factor into 20 intervals. Therefore, a total of 202 situations were evaluated, simulating the corresponding response factor of the neural network [51]. The simulated results have been investigated to get the maximum temperature response and its corresponding input variables. The optimization results are presented in Figures 3(a)-(c) & Figures 4(a)-(c) which reveals the exact values for the maximum predicted temperature and the corresponding coded input variables that have been obtained employing the ANN method. Table 2(a) shows the maximum predicted temperature together with the corresponding input variables and with those predicted from the RSM. These values were compared with those of the maximum experimental temperature ones of 1400, 1275, and 1550 and ![]()
of 178,200,132 at the centre line for D30, D60 and DFC discs respectively. The maximum predicted temperature by ANN is more closer to the corresponding experimental ones than those predicted by RSM. The maximum predicted temperatures have been compared to the analogous experimental ones and the absolute maximum deviation has been calculated employing the following equation:
![]()
(9)
Table 2(a) reveals the low values of % AD for the maximum predicted temperatures for ANN compared to that of RSM in all the studied cases for all discs.
13. Conclusions
An artificial neural mode was successfully developed and compared to RSM to predict the temperature profile of the three discs (D30, D60 & DFC) for three cases. The back propagation ANN network with Levenberg-Marquardt training algorithm was used to train the data from the experimental laboratory testing. The study outcome demonstrated that both statistical and computational intelligence modeling can make a potential alternative to time consuming experimental studies in addition to minimizing the costly machining test trial. The main conclusions obtained in this study are as follows:
1) The prediction results of the neural network model which have 10 neurons in hidden layer were found to be in good agreement with the experimental data.
2) The systematic comparative study has revealed that the properly trained ANN model has consistently performed more accurate prediction compared to those of RSM, in all aspects. The distribution of data points for neural network model almost similar and close to the actual experimental data with correlation coefficient (R) in the range of 0.9 - 1.0. This indicated that the developed neural network model is capable of making the prediction with good accuracy. This accurateness is expressed in the very high values of R2 and F_ratios and the very low value of error indicators for the ANN results compared to RSM ones.
3) Neural network is a powerful tool and is easy to use in complex or non-linear problems. This confirms that the ANN model displays a significantly higher generalization capacity than the rest of the RSM models. The reason can be accredited to the universal ability of ANN to approximate the nonlinearity of the system. The ANN predictive ability was proved to be better than that of RSM and it can be concluded that ANN gives a more accurate replacement of RSM.