The Impact of a Heterogeneous Surface on Spatiotemporal Uncertainties of Sensible Heat, Latent Heat, and CO₂ Flux Measured over the Secondary Forest

Nanami Sakai¹, Daisuke Komori¹, Masafumi Kon¹, Wonsik Kim²

¹Department of Civil Engineering, Tohoku University, Sendai, Japan.
²Institute for Agro-Environmental Sciences, National Agriculture and Food Research Organization, Tsukuba, Japan.

DOI: 10.4236/jwarp.2020.123011                

Abstract

The turbulent fluxes, such as sensible and latent heat fluxes and CO₂ flux, are globally observed over various terrestrial areas in order to understand the interaction between biosphere and atmosphere. Although the turbulent flux observations are generally performed on a horizontally homogeneous surface, the spatial distribution of the soil moisture is not homogeneous even on cultivated land with homogeneous vegetation, indicating that the development of each plant would be different and that the plant physiology, such as photosynthesis and growth, would be heterogeneous. In this study, to clarify the impact of a heterogeneous surface on spatiotemporal uncertainty of turbulent fluxes, a simultaneous flux observation experiment was conducted at different heights (20 m and 30 m) above the ground surface in a secondary seasonal tropical forest located in the Tak Province, Thailand. We defined ε as the spatial uncertainty of the turbulent flow flux, as proposed by Kim et al. (2011b) [1], and observed that ε of CO₂ flux was high, whereas ε of sensible and latent heat fluxes were low. This is likely to be caused by spatial uncertainty such as a heterogeneous surface. The CO₂ environment was heterogeneous; however, sensible and latent heat environments were homogeneous because the source area received insolation uniformly. Therefore, the analytical results for the CO₂ flux presented a different pattern from those exhibited by the analytical results of the latent and sensible heat fluxes.

Keywords

Eddy Covariance, Fractional Uncertainty, Monin-Obukhov Similarity Theory, Simultaneous Flux Observation

1. Introduction

Studies on turbulent diffusion have considerably progressed after Kolmogorov (1941) [2] derived a theoretical interpretation for the turbulent energy spectrum and after Obukhov (1946) [3] discovered that there was a scaling parameter for turbulent diffusion. Thereafter, Monin and Obukhov (1954) [4] derived a similarity theory based on the vertical wind speed in the surface boundary layer on a homogeneous surface, which can be referred to as the Monin-Obukhov similarity theory (MOST). The devices that can directly measure the turbulent diffusion, such as a sonic anemometer, were developed during the 1970s, with these devices initially being used for performing field-based flux experiments during the late 1980s. Various studies have focused on the interaction between the biosphere and atmosphere because of growing concerns over the impact of climate change on the terrestrial ecosystem. For example, the “FLUXNET” international network was established to monitor the heat, water, and CO₂ fluxes between the atmosphere and the land surface (Baldocchi et al. 2001 [5]). Further, the turbulence data are currently being collected at more than 500 flux observation sites from various vegetation zones, such as cultivated land and forests, across the world. Using these data, studies are being conducted to quantify the spatiotemporal variations in the global carbon stock and to estimate the global potential evapotranspiration based on biometeorology (Saegusa et al. 2008 [6]; Fisher and Baldocchi 2008 [7]). In addition, the collected heat, water, and CO₂ fluxes are extremely important for studies on the response of the terrestrial ecosystem to the regional differences in global climate change and for the development of models that are necessary to predict these responses.

The turbulent flux observations are generally performed on a horizontally homogeneous surface. There are two reasons for this observational constraint. First, because the eddy covariance method is used to calculate the fluxes from the observations, it can be assumed that material transport via advection can be ignored, and the vertical material transport is solely based on transport via turbulent flow. Second, the observed value is the weighted average of the material transported from the upwind source area via turbulent flow. Based on the wind direction and speed at the time of the observation, the impact on the source area may vary. If a surface area outside the study area is included in the source area, its impact will be included; therefore, the observation is conducted on a horizontally homogeneous surface.

However, the spatial distribution of the soil moisture is not homogeneous even on cultivated land with homogeneous vegetation, indicating that the development of each plant would be different and that the plant physiology, such as photosynthesis and growth, would be heterogeneous. Forests comprising diverse trees and forest floor vegetation are also heterogeneous in terms of plant physiology. The turbulent flux observations obtained from a heterogeneous surface exhibit different source areas based on the wind direction and speed, denoting that such a surface is theoretically unsuitable for obtaining such observations. However, there has been little discussion on the heterogeneity of the source areas despite considerable improvements in the performance and theoretical accuracy of the observational instruments over the previous three decades. Schmid and Lloyd (1999) [8] reported that it is important to conduct footprint analysis considering the observation altitude and atmospheric stability because the flux data obtained from a heterogeneous surface do not represent the footprint of the source area. In previous flux observations, in cases in which it was qualitatively confirmed that the MOST was established for analyzing the spectra of turbulent flow data for each time scale (30 minutes to two hours) without any issue, flux observation was empirically performed on the heterogeneous surfaces (Foken, 2006 [9]). However, even forest canopies that were considered to be homogeneous were reported to have spatiotemporal uncertainties in their sensible heat, latent heat, and CO₂ fluxes because of the impact of the ecosystem, and Oren et al. (2006) [10] showed that spatiotemporal uncertainty could lead to an error of a maximum of approximately 50% over a year while estimating the pure ecosystem CO₂ exchange using homogeneous vegetation. Therefore, it is important to quantitatively, rather than qualitatively, evaluate the impact of a heterogeneous surface on flux observations because the theoretical reliability of the flux observations is only valid up to a certain level of heterogeneity in the ground surface.

The eddy covariance method is the most extensively used method to measure the flux by directly measuring the turbulent diffusion. Recent studies have evaluated the spatiotemporal uncertainty ( $\delta$ ) generated during a flux analysis that uses the eddy covariance method. When the spatiotemporal uncertainty of the measured flux was initially discussed, it was suggested that $\delta$ comprised two elements. One element was the random error ( ${\delta }_r$ ), which was dependent on the stochastic nature of turbulent flow (Wesely and Hart, 1985 [11]) and was estimated from the standard deviation of a probability density function that followed a normal distribution centered on the true value when measured repeatedly. The other element was the systematic error ( ${\delta }_s$ ), which exhibited a certain impact on measurements (Abernethy et al. 1985 [12]). Therefore, majority of the studies on spatiotemporal uncertainty focused on both ${\delta }_r$ and ${\delta }_s$.

However, Vickers and Mahrt (1997) [13] proposed that unsteady fluctuations in data are another element of $\delta$, which was later recognized as the illegitimate error ( ${\delta }_i$ ). Therefore, it is assumed that $\delta$ includes ${\delta }_r$, which is derived from the limitations of the measurement devices and the unpredictable fluctuations in the measurement conditions, ${\delta }_s$, which is derived from the allowable error of the observational instruments and fundamental theory, and ${\delta }_i$, which is derived from the human error and incorrect instrument operation (Figure 1, Kim et al. (2011b)) (Bevington and Robinson, 2003) [14].

Finkelstein and Sims (2001) [15] derived a method for estimating $\delta$ as the sampling error based on statistical analysis. As the most recent study that estimated $\delta$ using such statistical analysis, Kim et al. (2011b) evaluated the fractional uncertainty ( $\epsilon$ ), which can be obtained by dividing $\delta$ with the flux at

Figure 1. Schematic of the manner in which the true and expected values are related with the associated errors. The expected value that is obtained from the observations (open circles) is indicated by the black circle (Kim et al., 2011b).

the time scale of the turbulent flow data. They further comparatively analyzed $\epsilon$ in various vegetation zones and denoted the potential of the $\epsilon$ -values for the sensible heat, latent heat, and CO₂ fluxes to converge to a same value irrespective of the spatiotemporal scale and the vegetation type.

The index ( $\epsilon$ ) that quantifies $\delta$, which has been proposed by Kim et al. (2011b), is defined in Equation (1).

$\epsilon =\frac{\delta }{\left|F\right|}=\frac{{\delta }_r+{\delta }_s+{\delta }_i}{\left|F\right|}\approx \frac{{\delta }_r+{\delta }_i}{\left|F\right|}$ (1)

${\delta }_s$ approaches zero for well calibrated instruments.

$\delta =\sqrt{Var\left\{q\right\}}$ (2)

$Var\left\{q\right\}=E\left\{{\left(q-E\left\{q\right\}\right)}^2\right\}=E\left\{q^2\right\}-E^2\left\{q\right\}$ (3)

$E\left\{q\right\}=\underset{N\to \infty }{\lim }\frac{1}{N}\underset{t=1}{\overset{N}{{\displaystyle \sum }}}{q}_t$ (4)

where F denotes the flux, q denotes the observation (where $q_t$ ( $t=1,2,\cdots ,N$ ) is the number of samples for a given observation at each time increment), E is the expected value. $\delta$ holds on Equation (2). According to Kim et al. (2011a [16] and 2015 [17]), ${\delta }_r$ is similar to white noise and is therefore considered constant (≈0.07, dashed line Fig.1 in Kim et al., 2011a), and $\epsilon$ combines ${\delta }_r$ with ${\delta }_i$, which is irregular and produced by deviations from an illegitimacy of the EC measurement assumption. Additionally, Kim et al. (2011b) proposed that $\epsilon$ would be proportional to ${\delta }_i$ which is the degree of the ground surface heterogeneity and atmospheric stationary. Therefore, a heterogeneous surface can be inferred by $\epsilon$.

The objective of this study is clarifying the impact of a heterogeneous surface on spatiotemporal uncertainty of sensible heat, latent heat, and CO₂ fluxes. In this study, a simultaneous flux observation experiment was conducted at different heights (20 m and 30 m) above the ground surface in a secondary seasonal tropical forest located in the Tak Province, Thailand, to use theoretical analysis using the MOST and $\epsilon$.

2. Dataset and Methods

2.1. Dataset

The observational data were collected from an observation tower located in the Tak, Thailand (N16.56.24, E99.25.48). It is surrounded by a secondary seasonal tropical forest with heterogeneous vegetation, including deciduous trees and evergreens (refer to Kim et al. (2014) [18] for further site details and aerial photo).

We installed a three-dimensional (3D) sonic anemometer (CSAT3; Campbell Scientific, Utah, USA) and an open path CO₂/H₂O analyzer (LI7500; LI-COR, Nebraska, USA) at 20- and 30-m heights, respectively, on the observation tower and collected the vertical and horizontal wind speeds, temperature, and CO₂ and H₂O concentrations at a 10-Hz sampling frequency from June 5 to August 26, 2010. The vegetation height surrounding the observation tower was 7 m. We calculated the hourly sensible heat, latent heat, and CO₂ fluxes from the observational data using the eddy covariance method.

2.2. Method 1: Evaluation of Consistency of Surface Homogeneity

The vertical wind speed profile in the surface boundary layer can be obtained using Equation (5), which is based on the MOST.

$\frac{\text{d}\bar{u}}{\text{d}z}=\frac{u_{*}}{\kappa z}\cdot {\varphi }_m\left(\frac{z}{L}\right)$ (5)

${\varphi }_m={\left(1-16\cdot \frac{z}{L}\right)}^{-\frac{1}{4}}$ (6)

where $\bar{u}$ denotes the hourly averaged horizontal wind speed, z denotes the height above the surface, $u_{*}$ denotes the friction velocity, $\kappa$ denotes the von Kármán constant, L denotes the Obukhov length, and ${\varphi }_m$ denotes the non-dimensional shear function (Dyer and Hicks, 1970) [19], which is obtained using Equation (6). We calculated $F_{*}$ to evaluate the consistency between the magnitudes of the turbulent flow observations at 20 and 30 m using the MOST.

$F_{*}=\frac{F}{{\varphi }_m}$ (7)

where the fluxes at 20 and 30 m are denoted as $F_{\ast 20\text{m}}$ and $F_{\ast 30\text{m}}$, respectively. If the magnitudes of the turbulent flow observations at 20 m and 30 m were from source area with similar heterogeneity, $F_{\ast 30\text{m}}$ and $F_{\ast 20\text{m}}$ should be same values. In addition, impact of atmospheric stationarity on $F_{\ast 30\text{m}}$ and $F_{\ast 20\text{m}}$ should be also same on the simultaneous flux observation experiment at 20 and 30m. Therefore, we state that the differences of source areas for $F_{\ast 20\text{m}}$ and $F_{\ast 30\text{m}}$ can be expressed increasingly consistent as $F_{\ast 30\text{m}}/F_{\ast 20\text{m}}$ approaches 1 in this study. Note that in terms of consistency, $F_{\ast 30\text{m}}/F_{\ast 20\text{m}}$ approaches 1 when the source areas of $F_{\ast 20\text{m}}$ and $F_{\ast 30\text{m}}$ have similar heterogeneity. We calculated $F_{\ast 30\text{m}}/F_{\ast 20\text{m}}$ for the CO₂, latent heat, and sensible heat fluxes ( $F_{\ast 30\text{m}}/F_{\ast 20\text{m}}\left({\text{CO}}_{\text{2}}\right)$, $F_{\ast 30\text{m}}/F_{\ast 20\text{m}}\left(\text{lE}\right)$, and $F_{\ast 30\text{m}}/F_{\ast 20\text{m}}\left(\text{H}\right)$, respectively).

Method 2: Calculation of the spatiotemporal uncertainty for the turbulent flow fluxes

In accordance with the method proposed by Kim et al. (2011b), we calculated F and $\delta$ to determine using Equation (1). Further, we calculated for the CO₂, latent heat, and sensible heat fluxes ( ${\epsilon }_{{\text{CO}}_{\text{2}}}$, ${\epsilon }_{\text{lE}}$, and ${\epsilon }_{\text{H}}$, respectively). Please refer to Kim et al. (2011b) for further details.

2.3. Data Selection

Only the optimal data examined by Methods 1 and 2 can be used for this research. Therefore, data was strictly selected by the following processes:

1) Because a stable atmosphere inhibits the development of the turbulent flow, we excluded the data where the atmospheric stability was greater than 1.

2) We also excluded the observations where simultaneous sensible heat, latent heat, and CO₂ fluxes were not obtained for Method 1. In addition, temporal uncertainties were same because we only used the flux data observed simultaneously. It means that $\epsilon$ represents the spatial uncertainty where each $\epsilon$ were different.

3) Further, because the consistency of surface homogeneity, $F_{\ast 30\text{m}}/F_{\ast 20\text{m}}$, was compared examined with the spatiotemporal uncertainty of the turbulent flow observations at 20 m, ${\epsilon }_{20\text{m}}$, we only selected the data where the ${\epsilon }_{30\text{m}}/{\epsilon }_{20\text{m}}$ ratio was close to 1 ( $0.9<{\epsilon }_{30\text{m}}/{\epsilon }_{20\text{m}}<1.1$ ), which means spatiotemporal uncertainty were similar at 20 and 30 m heights.

Table 1 presents the number of analyzed data during each step of the data selection process. Finally, the number of optimal data for this research was 48 which weren’t included ${\delta }_i$ excluding surface heterogeneity. In addition, because the surface heterogeneity isn’t instantly changed, many and/or continuous data isn’t necessary in this research.

3. Results

Figure 2 depicts the relation between ${\epsilon }_{{\text{CO}}_2\left(20\text{m}\right)}$ (spatiotemporal uncertainty) obtained via the 2-(3) method 2 and $F_{\ast 30\text{m}}/F_{\ast 20\text{m}}\left({\text{CO}}_{\text{2}}\right)$ (consistency of the surface heterogeneity) obtained via the 2-(2) method 1. The following three key groups are observed in the data: large $F_{\ast 30\text{m}}/F_{\ast 20\text{m}}\left({\text{CO}}_{\text{2}}\right)$ values (>2.0; triangles), small $F_{\ast 30\text{m}}/F_{\ast 20\text{m}}\left({\text{CO}}_{\text{2}}\right)$ values (≤2.0) with ${\epsilon }_{{\text{CO}}_2\left(20\text{m}\right)}<0.15$ (circles), and smaller $F_{\ast 30\text{m}}/F_{\ast 20\text{m}}\left({\text{CO}}_{\text{2}}\right)$ values (≤2.0) with ${\epsilon }_{{\text{CO}}_2\left(20\text{m}\right)}\ge 0.15$ (crosses). Figure 3 and Figure 4 denote the relation between $\epsilon$ and $F_{\ast 30\text{m}}/F_{\ast 20\text{m}}$ for the sensible and latent heat fluxes, respectively. Further, we used the same symbols for the sensible and latent heat fluxes measured at the same time as the CO₂ flux in Figure 2 to compare the relation between $\epsilon$ and $F_{\ast 30\text{m}}/F_{\ast 20\text{m}}$ for each flux.

Figure 5 was divided into four sectors to delineate the observed heterogeneities in the CO₂ environment. The upper left sector ( $F_{\ast 30\text{m}}/F_{\ast 20\text{m}}>2.0$ and ${\epsilon }_{{\text{CO}}_2\left(20\text{m}\right)}<0.15$ ) is given an A classification and corresponds to the area denoted

Table 1. Number of data for each selection stage.

Figure 2. Relation between and.

Figure 3. Relation between and.

by the triangles in Figure 2. The upper right sector (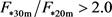and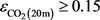) is given a B classification. The lower left sector (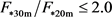and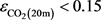) is given a C classification and corresponds to the area denoted by circles in Figure 2. The lower right sector (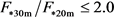and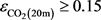) is given a D classification and corresponds to the area denoted by crosses in Figure 2. As presented in Table 2, the CO₂ fluxes in the A classification sector in Figure 5 exhibit a relatively low consistency with a low spatiotemporal uncertainty, whereas those in the B classification sector also exhibit

Figure 4. Relation between and.

Figure 5. Classification. In this study, upper limit of vertical axis was 4.0, lower limit of vertical axis was 0.5 (vertical axis decrease inversely when it less than 1).

Table 2. Classification methods and characteristics.

a relatively low consistency with a high spatiotemporal uncertainty. Regarding CO₂ fluxes in the A classification, the heterogeneities of source areas at 20 and 30 m were different but the spatiotemporal uncertainties of both source areas were low (observed values were close to Q (true value)).

It means that the surface heterogeneity of source area at 20 and 30 m were different but both of surface heterogeneity have little impact on. Here, we only selected the optimal data during the 2-(4) data selection process, CO₂ fluxes in the B classification sector were excluded. CO₂ fluxes in the C classification exhibit a high consistency (source area at 20 and 30 m have same heterogeneity) with low spatiotemporal uncertainty. Namely, it means the source area at 20 and 30 m were homogeneous. On the other hand, those in D classification also exhibit a high consistency (source area at 20 and 30 m have same heterogeneity) but high spatiotemporal uncertainty. Namely, it means that source area at 20 and 30 m were heterogeneous.

As depicted in Figures 2-4, some of the CO₂ flux results were assigned a D classification (crosses in Figure 2), whereas some were assigned a C classification due to and for the sensible and latent heat environments. Furthermore, an analysis based on the MOST denoted that the CO₂ fluxes with an A classification (triangles in Figure 2) were assigned either C or D classifications for the sensible and latent heat fluxes (triangles in Figure 3 and Figure 4), indicating high consistencies in the sensible and latent heat environments. However, there were also latent heat fluxes with a D classification and a relatively high spatiotemporal uncertainty (triangles in Figure 4). The source areas for the latent heat fluxes at 20 and 30 m exhibited similarly high spatiotemporal uncertainty, leading to high consistencies. However, the source areas for the sensible heat fluxes at both 20 and 30 m have low spatiotemporal uncertainty, because all the sensible heat fluxes were assigned a C classification, with high consistencies and low spatiotemporal uncertainties.

4. Discussion

The CO₂ flux results were assigned a D classification (crosses in Figure 2), whereas the corresponding sensible heat and latent heat flux results were assigned a C and D classification (crosses in Figure 3 and Figure 4). It means that sensible heat and latent heat fluxes tended to have low spatial uncertainty compare with CO₂ flux because we only used the optimal data which temporal uncertainty were same. Some of sensible heat and latent heat flux results which were assigned a D classification in Figure 3 and Figure 4 had same temporal uncertainty as CO₂ flux results. However, those in a C classification in Figure 3 and Figure 4 had different spatial uncertainty from CO₂ flux results. It is able to be considered that different spatial uncertainty was attributed to a heterogeneous surface. The surface heterogeneity on the sensible heat and latent heat flux are homogeneous but not on CO₂ flux.

The CO₂ flux results were assigned an A classification (triangle in Figure 2), whereas the corresponding sensible heat flux results were assigned a C classification (triangle in Figure 3). It means that the source area at 20 and 30 m of sensible heat was similarly homogeneous. In addition, almost all latent heat flux results were also assigned a C classification (triangle in Figure 4). It means that the source area at 20 and 30 m of latent heat had same surface heterogeneity and some of them were heterogeneous but some of them were homogeneous.

One of reasons why the analytical results for the CO₂ flux presented a different pattern from those exhibited by the analytical results of the sensible and latent heat fluxes was considerable from the different impact of the insolation on sensible, latent, and CO₂ fluxes. The degree of ground surface heating is proportional to the insolation, which indicates that the increase in sensible and latent heat fluxes are strongly proportional to the insolation. Although latent heat and CO₂ fluxes, namely transpiration and photosynthesis, are also corresponding to the insolation, these are also regulated with the amount of water in the plant body, and photosynthesis is constant (saturated) under the fine insolation as described by many previous researches (cf. light response curve of photosynthesis (Monsi and Saeki, 1953) [20]).

For the above reasons, the amount of water in the plant body and some other factors (cf. stomatal conductance, vegetation, etc.) increase the spatial uncertainties of CO₂ flux; and the surface heterogeneity of source area of CO₂ flux was higher than source area of latent heat and sensible heat fluxes. In addition, although and were empirically used for the data classification in this study, further investigations of the physical meaning of these value would be needed.

5. Conclusion

We defined as the spatial uncertainty of the turbulent flow flux, as proposed by Kim et al. (2011b), and observed that was high, whereas and were low. This is likely to be caused by spatial uncertainty such as a heterogeneous surface. The CO₂ environment was heterogeneous; however, sensible and latent heat environments were homogeneous because the source area received insolation uniformly. Therefore, the analytical results for the CO₂ flux presented a different pattern from those exhibited by the analytical results of the latent and sensible heat fluxes.

Acknowledgements

We thank Grants-in-Aid for Scientific Research (15K20858，supervisor: Daisuke KOMORI) and the Masaki SAWAMOTO research grant for providing funding to conduct and publish the research presented in this study, respectively.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Kim, W., Komori, D. and Cho, J. (2011) The Characteristic of Fractional Uncertainty on Eddy Covariance Measurement. Journal of Agricultural Meteorology, 67, 163-171. https://doi.org/10.2480/agrmet.67.3.10
[2]	Kolmogorov, A.N. (1941) Local Structure of Turbulence in an Incompressible Viscous Fluid at Very Large Reynolds Numbers. Doklady Akademiia Nauk, 30, 301-305.
[3]	Obukhov, A.M. (1946) Turbulentnost’ v temperaturnoj-neodnorodnoj atmosfere (Turbulence in an Atmosphere with a Non-Uniform Temperature). Trudy Instituta, 95-115.
[4]	Monin, A.S. and Obukhov, A.M. (1954) Basic Laws of Turbulent Mixing in the Surface Layer of the Atmosphere. Trudy Geofiz, Instituta Akademii Nauk, 24, 163-187.
[5]	Baldocchi, D., Falge, E., Gu, L., Olson, R., Hollinger, D., Running, S., Anthoni, P., Bernhofer, C., Davis, K., Evans, R., Fuentes, J., Goldstein, A., Katul, G., Law, B., Lee, X., Malhi, Y., Meyers, T., Munger, W., Oechel, W., Paw, K., Pilegaard, K., Schmid, H., Valentini, R., Verma, S., Vesala, T., Wilson, K. and Wofsy, S. (2001) FLUXNET: A New Tool to Study the Temporal and Spatial Variability of Ecosystem-Scale Carbon Dioxide, Water Vapor, and Energy Flux Densities.Bulletin of the American Meteorological Society, 82, 2415-2434. https://doi.org/10.1175/1520-0477(2001)082<2415:FANTTS>2.3.CO;2
[6]	Saegusa, N., Yamamoto, S., Hirata, R., Ohtani, Y., Ide, R., Asanuma, J., Gamo, M., Hirano, T., Kondo, H., Kosugi, Y., Li, S., Nakai, Y., Takagi, K., Tani, M. and Wang, H. (2008) Temporal and Spatial Variations in the Seasonal Patterns of CO2 Flux in Boreal, Temperature, and Tropical Forests in East Asia. Agricultural and Forest Meteorology, 148, 700-713. https://doi.org/10.1016/j.agrformet.2007.12.006
[7]	Fisher, J., Tu, K. and Baldocchi, D. (2008) Global Estimates of the Land-Atmosphere Water Flux Based on Monthly AVHRR and ISLSCP-II Data, Validated at 16 FLUXNET Sites. Remote Sensing of Environment, 112, 901-919. https://doi.org/10.1016/j.rse.2007.06.025
[8]	Schmid, H.P. and Lloyd, C.R. (1999) Spatial Representativeness and the Location Bias of Flux Footprints over Inhomogeneous Areas. Agricultural and Forest Meteorology, 93, 195-209. https://doi.org/10.1016/S0168-1923(98)00119-1
[9]	Foken, T. (2006) 50 Years of the Monin-Obukhov Similarity Theory. Boundary-Layer Meteorology, 119, 431-447. https://doi.org/10.1007/s10546-006-9048-6
[10]	Oren, R., Hsieh, C., Stoy, P., Albertson, J., Mccarthy, H., Harrell, P. and Katul, G. (2006) Estimating the Uncertainty in Annual Net Ecosystem Carbon Exchange: Spatial Variation in Turbulent Fluxes and Sampling Errors in Eddy-Covariance Measurements. Global Change Biology, 12, 883-896. https://doi.org/10.1111/j.1365-2486.2006.01131.x
[11]	Wesely, M.L. and Hart, R.L. (1985) Variability of Short Term Eddy-Correlation Estimates of Mass Exchange. U.S. Environmental Protection Agency, Washington DC, 591-612. https://doi.org/10.1007/978-94-009-5305-5_35
[12]	Abernethy, R.B., Benedict, R.P. and Dowdell, R.B. (1985) ASME Measurement Uncertainty. Journal of Fluids Engineering, 107, 161-164. https://doi.org/10.1115/1.3242450
[13]	Vickers, D. and Mahrt, L. (1997) Quality Control and Flux Sampling Problems for Tower and Aircraft Data. Journal of Atmospheric and Ocean Technology, 14, 512-526. https://doi.org/10.1175/1520-0426(1997)014<0512:QCAFSP>2.0.CO;2
[14]	Bevington, P.R. and Robinson, D.K. (2003) Data Reduction and Error Analysis for the Physical Science. McGraw-Hill, New York.
[15]	Finkelstein, P. and Sims, P. (2001) Sampling Error in Eddy Correlation Flux Measurements. Journal of Geophysical Research: Atmospheres, 106, 3503-3509. https://doi.org/10.1029/2000JD900731
[16]	Kim, W., Cho, J., Komori, D., Aoki, M., Yokozawa, M., Kanae, S. and Oki, T. (2011) Tolerance of Eddy Covariance Flux Measurement. Hydrological Research Letters, 5, 73-77. https://doi.org/10.3178/hrl.5.73
[17]	Kim, W., Miyata, A., Ashraf, A., Maruyama, A., Chidthaison, A., Jaikaeo, C., Komori, D., Ikoma, E., Sakurai, G., Seoh, H., Son, I., Cho, J., Kim, J., Ono, K., Nusit, K., Moon, K., Mano, M., Yokozawa, M., Baten, M.A., Sanwangsri, M., Toda, M., Chaun, N., Polsan, P., Yonemura, S., Kim, S., Miyazaki, S., Kanae, S., Phonkasi, S., Kammales, S., Takimoto, T., Nakai, T., Iizumi, T., Surapipith, V., Sonklin, W., Lee, Y., Inoue, Y., Kim, Y. and Oki, T. (2015) Flux Pro as a Realtime monitoring and Surveying System for Eddy Covariance Flux Measurement. Journal of Agricultural Meteorology, 71, 32-50. https://doi.org/10.2480/agrmet.D-14-00034
[18]	Kim, W., Komori, D., Cho, J., Kanae, S. and Oki, T. (2014) Long-Term Analysis of Evapotranspiration over a Diverse Land Use Area in Northern Thailand. Hydrological Research Letters, 8, 45-50. https://doi.org/10.3178/hrl.8.45
[19]	Dyer, A. and Hicks, B. (1970) Flux-Gradient Relationships in the Constant Flux Layer. Quarterly Journal of the Royal Meteorological Society, 96, 715-721. https://doi.org/10.1002/qj.49709641012
[20]	Monsi, M. and Saeki, T. (1953) über den Lichtfaktor in den Pflanzengesellschaften und seine Bedeutung für die Stoffproduktion. Japanese Journal of Botany, 14, 22-52.