A Transshipment Model of Seven-Up Bottling Company, Benin Plant, Nigeria ()
1. Introduction
Transportation is a very important subsystem of logistics in terms of value and its cost takes a large portion of costs in such logistics system [Briš [1] ]. It is therefore an important part of production process. Operations managers are constantly searching for ways of getting their goods/services to their customers that will be cost-effective, meet international best practice and at the same time increase the profit margin of their organization. More so due to demand variability and market uncertainty, achieving this transportation goal requires a lot of flexibility, short response time and development of new innovative solutions for reaching the customers [Noham and Tzur [2] ]. This transportation need becomes more complicated when challenges arise from globalization, increase market competition, and accelerated technology development is considered.
With the introduction of Operations Research and in particular linear programming and networking to subject areas like statistics and management, operations managers can now deal with this challenging need. Among the many linear programming problems introduced by Operations Research is the Transportation Problem. The transportation problem introduced as far back as the 1940s has received wide acceptance over the years with many researchers making several improvements to suit their peculiar/present needs.
The typical transportation problem deals with the distribution of goods from several points of supply to a number of points of demand. This problem usually arises when a cost-effective pattern is needed to ship/transport items from origins that have limited supply to destinations that have demand for the goods. It also refers to a class of linear programming problems that involve selection of most economical shipping/transportation routes for transfer of a uniform commodity from a number of sources to a number of destinations [Khurana [3] ].
Like all linear programming problems (LPP), the transportation problem has its objective function and constraints. The most common objective function is to schedule shipments from sources to destinations so that total production and transportation costs are minimized [Slide Share [4] ]. And the constraints are that the resources to be optimally allocated usually involve a given capacity of goods at each source and a given requirement for the goods at each destination. For the transportation problem, the source/supply points can only send out goods but cannot receive any while the sink or the demand point can only accept goods and not give out. With the diversification commodity type, size, distance to sinks etc., this transportation model becomes limited at some point. To overcome this limitation, a variant of the transportation problem with an intermediate point was introduced. This is known as the Transshipment problem.
A transshipment is defined as the transfer of stock between two locations at the same level of the inventory/distribution system. The problem is to determine replenishment quantities and how much to transship each period so as to satisfy deterministic dynamic demand at each location at minimal cost. The planning horizon is finite and no back orders are allowed [Herer and Tzur, [5] ]. It can also be seen as transportation of goods/containers to an intermediate destination, before it is shipped to another destination. There may be several reasons for such a change. One of which is to trans-load i.e. changing the means of transport during the journey (either from a land to an air, etc.). Other reasons could be to combine small shipments into a large shipment (consolidation), dividing the large shipment at the other end (deconsolidation). Whatever the reason, this model takes into consideration a multi-phase transport system where the flow of material-raw and/or finished goods and services are taken through the intermediate point which is between the origin and the destination. The whole stock is expected to pass through these points of reloading before the goods are finally sent to their destination [Briš [1] ].
Though the transshipment problem is an extension or improvement to the transportation problem its optimum solution is found by easily converting the transshipment problem into an equivalent transportation problem and solving using the usual transportation techniques. The availability of such a conversion procedure significantly broadens the applicability of the algorithm for solving transportation problems. The conventional Transportation Problem can be represented as a mathematical structure which comprises an Objective Function subject to certain Constraints. In classical approach, transporting costs from M sources or wholesalers to N destinations or consumers are to be minimized. It is an Optimization Problem which has been applied to solve various NP-Hard Problems [Chaudhuri and De [6] ].
To obtain the optimum solution for the converted transshipment problem the LPP will be solved in 2 two stages. In first stage involves obtaining the Initial Basic Feasible Solution (IBFS) using available methods such as North West Corner, Least Cost Method, and Vogel’s Approximation Method (VAM). The second stage employs the use of Modified Distribution Method (MODI) and the Stepping Stone Method from the IBFS to finally obtain the optimal solution [Patel and Bhathawala [7] ]. Other newer methods have been proposed by Sudhakar et al., [8] and Pandian and Natarajan [9] .
As previously stated, the foremost concern of every manufacturer is the need to get his products from the plants/warehouse to the consumer/final destination where it is most demanded. For the manufacturer therefore transporting and/or transshipping is the key to achieving this. The question therefore is the best way to go about this considering the costs involved and also to make profits. The aim of the study is to model the transportation/distribution of the product as a transshipment problem in other to obtain the minimum cost.
2. Literature Review
The transshipment problem is dated back to the medieval times when trading started becoming a mass phenomenon. The concept takes into account a transportation model in which any of the origin and destination can serve as an intermediate point through which goods can be temporarily received and then transshipped to other points or to the final destination [Gass, 1969: cited by Briš, [1] ]. It further considers that within a given time period each shipping source has a certain capacity and each destination has certain requirements with a given cost of shipping from source to destination. The Objective Function is to minimize total transportation costs and satisfy destination requirements within source requirements [Gupta and Mohan [10] ].
The major focus in the transshipment problem was to initially obtain the minimum-cost and/or shortest transportational route, however due to technological development the minimum-durational transportation problems are now being studied. In recent times other researchers have extensively studies this Linear Programming Problems and developed different variants based on the needed objective function.
Among recent literatures, researchers like Khurana et al., [11] studied the minimum-duration transshipment problem. Their study proposed an algorithm that solves the original transshipment problem by transforming it into an equivalent transportation problem. This algorithm finds out the optimal time for transportation from origins to destinations with transshipment. Khurana [12] also used the transshipment technique to find the shortest route from one point in a network to another point. This model is also very useful for reducing the cost of transportation. The study focused on the shortest route problem as against those earlier mentioned. Khurana formulated a three-dimensional linear transshipment problem based on the assumption that there exist certain constraints that may sometimes arise from the production budget or politically induced, the total flow of transportation is specified by some external decision maker which thereby results in restricted and enhanced flow in the market. The optimal solution of this problem is of practical interest to operation’s managers facing such peculiar challenge [Khurana [12] ].
The transshipment problem characterized by the uncertainty relative to customer demands and transfer lead time was studied by Hmiden et al. [13] . For them identifying a transshipment policy that incorporates the fuzziness of customer demands and transfer lead times and determining the approximate replenishment quantities which minimize the total inventory cost was the main focus while using a distribution network of one supplier with several locations selling the product. Their method was centered on the use of expert judgments to evaluate customer demands and the transfer lead time which they represented by fuzzy sets. Among other factors studied on the expert judgments, they used the behavior types of the decision maker (pessimistic and optimistic) to determine the precise transshipment decision moment and the transshipment quantity.
Transshipment problem is characterized by a dynamic network with several sources and sinks and that there were no polynomial-time algorithms known for most of transshipment problems [Hoppe and Tardos [14] ]. Hoppe and Tardos gave the first polynomial-time algorithm for the quickest transshipment problem that provided an integral optimum flow.
Tadei et al. [15] pointed out in their research that the transportation process takes place in two stages for any transshipment problem. These were: 1) from origins to transshipment facilities, 2) from transshipments facilities to final destinations. By economic implication, the process could incure three kinds of cost: 1) the fixed cost of locating a transshipment facility, 2) the transportation cost from an origin to a destination through a transshipment facility, 3) the throughput operation cost at each transshipment facility. Their study sought to reveal the overall cost implication involved in the entire transshipment process that may not be incorporated in the transshipment LPP.
Still dealing with the overall cost implication, Kestin and Uster [16] added that the throughput operations cost are generated by the freight treatment operations, such as loading/unloading, but also to inventories and postponed processing, such as packaging, testing etc. While the fixed cost and the transportation cost are usually well defined, easy to determine and measure, the throughput operation cost is vague, stochastic and cannot be easily measurable, so that their probability distribution remains in general unknown [Tadei et al. [17] ].
The multi-objective transshipment problem (MOTP) is another model that was studied by Das et al. [17] , Abd El-Wahed [18] , Saraj and Mashkoorzadeh [19] and Malakooti [20] .
Apart from the different objective functions describe above, other researchers had focused on the transshipment center problem instead of the transshipment itself. Previous studies have shown that the transshipment center problem is important in dealing with transshipment in a supply chain management. It was noted that most of the relevant existing research focused on networking and do not consider the dynamics of the configurations in transshipment center units [Perng and Ho, [21] ].
Ameln and Fuglum [22] introduced the use of transshipment to the liner shipping network designs which was less common a few decades ago. They noted that transshipment was not included when considering route planning for liner shipping network as at the early 1990s. Meng et al. [23] tend to agree with them that 8 out of 12 of the studies on fleet deployment did not consider transshipment. Notteboom and Rodrigue [24] stated that the use and influence of transshipment on the liner shipping network design was described and whether or not transshipment operations are allowed between the routes differ based on each researcher. On the other hand some other researchers argue that transshipment of goods is frequently occurring in liner shipping and the associated cost should not be ignored when designing the network. Ameln and Fuglum also concluded that the first exact solution methods to the LS-NDP (Liner Shipping Network Designs Problem) with transshipment cost was presented in their paper [Ameln and Fuglum, [22] ]; Reinhardt and Pisinger [25] .
Agarwal and Ergun [26] studied transshipment in their research without any consideration on the cost implication. Ameln and Fuglum [21] however concluded that when the transshipment cost is not taken into account the transshipment in the optimal solution will probably be inappropriately large. Husain et al. [27] ; Gupta et al. [28] ; Birla et al. [29] ; Deepmala [30] ; Mishra [31] .
Whatever the reason for the study of the transshipment problem, the basic mathematical formulation is still the same though with slight variations. The typical transshipment model is given below.
The formulation of the transshipment problem requires certain initial basic assumptions these are:
• The system consists of m origins and n destinations, where
,
• Homogenous set of goods are available for shipping.
• The required amount of good at the destinations equals the produced quantity available at the origins.
• Transportation simultaneously starts at the origins and is possible from any node to any other (also to an origin and from a destination).
• Transportation costs are independent of the shipped amount.
Notations
• cr,s: cost of transportation from node r to node s.
• ai: goods available at node i.
• bm+j: demand for the good at node (m + j).
• xr,s: actual amount transported from node r to node s.
The goal is to minimize
subject to:
•
•
•
•
3. Methodology
The Seven-Up bottling company Plc is one of the largest independent manufacturer and distributor of the well-known and widely consumed brands of soft drinks in Nigeria. They are the producers of Pepsi, 7 UP, Mirinda, Teem and Mountain Dew brand. The Benin production plant is one among the many plants owned by the company in Nigeria. A simple random sampling of the weekly demand and supply chain for the plastic Pepsi 50 cl soft drink was used for the analysis. This sample is necessary as it will reflect the typical operations of the demand and supply of the company in question.
3.1. Method
The data collected from the Benin production plant was properly summarized into tables (Table 1 and Table 2) to indicate the sources which is the production plants and its subsequent capacity, the transshipment points known as the deports and the demand points which are the retails outlets that are being serviced by the plant. This transshipment data was transformed to a transportation problem which is ideal for solving such LPP (Table 3). The TORA Operations Research Windows Version 2.00 Software was used for the analysis.
![]()
Table 1. Transportation cost per crates of Pepsi 50 cl per week from Benin to the transshipment points.
3.2. The Transshpment Model
The general linear programming model of a transshipment problem is
Subject to
where
xij = Amount of unit shipped from node i to node j.
cij = Cost per unit of shipping from node i to node j.
si = Supply at origin node i.
dj = Demand at sink node j.
3.3. Data Analysis
This section is concerned with the presentation of data, its analysis and summary of the findings. For clarity the various key points in the transshipment model are listed out below;
• The Benin plant serves as the source of the 50 cl Pepsi soft drink and its weekly supply is 10,000 crates to Sapele and Warri environs.
• The transshipment points are Swift, Frendo, Clement Vents, Life Dew, Osoro, Afoke, Temi & Oris, Best Beer, Stella Chukwu and Oriemu Vents (These are actual mega distributors within Sapele and Warri LGAs of Delta State).
• While the demand points are in the respective towns/location in Delta State of Nigeria. They include Jesse, Mosogar, Koko, Oghara, Gana, Amukpe, Jakpan, Effurun, Osubi, Igbudu and Adeje towns. These demand points have varying capacities based on their consumption of the crates per week.
A source is a point that can only send products to other points but cannot receive any products. Similarly, a sink is defined as a point that can only receive products from other points but cannot send products. Then, a transshipment point is defined as a point that can both receive products and also send products to other points. Therefore, this model consists of a problem with 1 source, 11 sinks, and 10 transshipment points as shown in Figure 1.
The crates of Pepsi 50 cl soft drinks are transported by road. Full trailer load consists of 800 crates of the products this gives above 12 trailer loads weekly. The cost of transportation per crate of the product is presented in Table 1 and Table 2.
The figures from the above tables can be converted into the transportation tableau with their respective transportation costs as shown in Table 3.
3.4. Mathematical Representation of Problem
The mathematical representation of Xij = amount to be transported from ith node
![]()
Figure 1. The flow of the product to be transshipped per week from the plant (source) through the transshipment points to the demand points (sinks). Note: ST (Sapele Town); WT (Warri Town).
to jth node;
;
. Note: All costs are in Naira (N)
Subject to
(Supply point constraint)
(Demand point constraints)
(Transshipment point constraints)
3.5. Computational Procedure
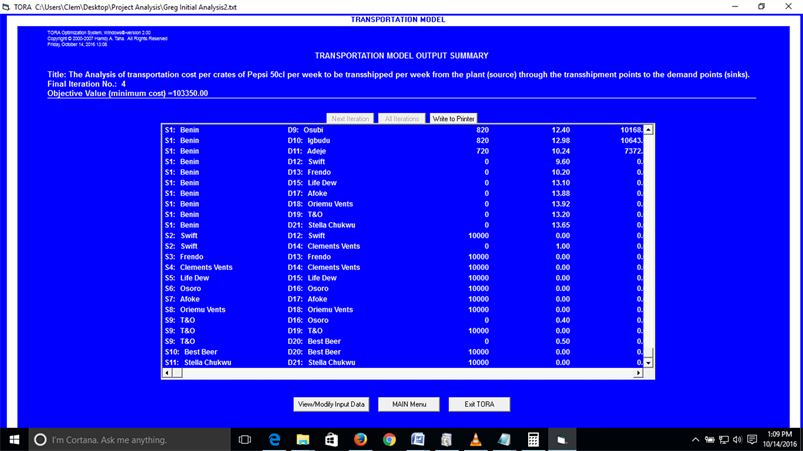
The data was imputed and analyzed with the TORA Windows Version 2.00 software. The software made 14 iterations to obtain the optimum solution with a total cost of N103,350.00 as the minimum cost that satisfies the objective function. The result is shown in Table 4. Figure 2 shows the route which satisfies the objection function.
As can be seen from the analysis, the total cost = N9.11 (720) + 9.73 (820) + 9.30 (320) + 9.11 (730) + 9.11 (730) + 9.00 (1200) + 11.01 (1300) + 11.23 (1200) + 12.40 (820) + 12.40 (820) + 12.98 (820) + 10.24 (720) = N103,350.00.
4. Discussion, Conclusion and Recommendations
As can be seen from the analysis, the best route to obtain the minimum cost can be summarized in Table 5 with the optimum cost of transporting the crates of 50 cl pepsi found to be N103,350.00. This value represents the minimum cost that the company can transport 10,000 crates of 50 cl Pepsi soft drinks to their esteem costumers within the major towns in Sapele and Warri LGAs of Delta State Nigeria.
This can be achieved if Benin Plant transports the product directly to the various demand points namely Jesse, Koko, Oghara, Mosogar and Gana (in the Sapele region) and Jakpan, Effurun, Osubi, Igbudu and Adeje (in the Warri region). The analysis from the TORA software is shown in Appendix B.
4.1. Recommendation
We wish to recommend that the Seven-up Bottling Company adapts this result of
![]()
Figure 2. The flow of the product from the plant (source) to the demand points (sinks) that satisfies the optimum solution. Note: ST (Sapele Town); WT (Warri Town).
![]()
Table 5. Showing the optimum cost for transshipping 50 cl Pepsi.
transporting the product obtained by the analysis so that their cost of transporting 50 cl Pepsi soft drinks within the Benin-Sapele/Warri region can be drastically minimized.
4.2. Suggestions
This study was conducted using primary data and with the findings derived, it can be a source of more information to other researchers who may wish to improve on the limitations of this study to cover areas like minimum duration problems, transshipment facility layout problem/labour and man-power related issues, the shortest route problem and so on. Therefore, more research and studies can still be carried out to look into these other areas on the transshipment model.
Appendix A
Screen shots from the TORA Windows Version 2.00 software.
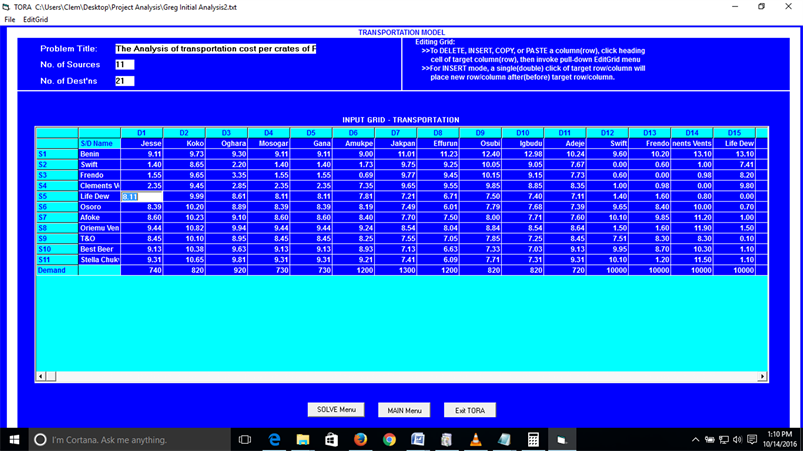
(a) Initial data before analysis.
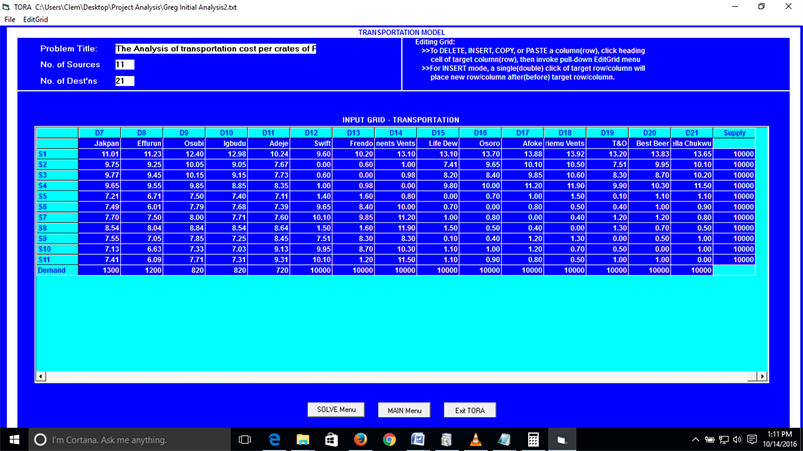
(b) Continuation of the Initial data before analysis.

(c) The optimum solution and respective allocations.
(d) Continuation of the optimum solution and respective allocations.