1. Introduction
Forests play a significant role in sustaining economy, ecology and social development and growth (Chakravarty et al., 2011). The ecological function and economic values of forests, which often expressed in terms forest biomass and volume, require a reliable method of estimation (Djomo et al., 2010; Günlü et al., 2014). Direct measurement of volume and biomass in most cases gives a reasonable accuracy, however, employing field measurement especially in large-scale plantation projects is quite expensive, labour-intensive, mostly destructive, time-consuming and sometimes impracticable (Li & Xiao, 2007; Ounban et al., 2016). Thus, estimation of volume and biomass using allometric equations which can represent the field measurement for large-scale industrial plantations is highly advisable (Lehtonen et al., 2004; Zianis et al., 2005; Oyamakin, 2011). Forest growth models have the ability of describing the development of tree crops with specific time changes, species and sites (Hjelm, 2015). There are various types of forest models including tapper model, crown models, however, total tree volume and biomass models are the commonly applied models in forest management planning, estimating the forest volume, tree biomass, carbon content and evaluating the ecological roles forests (Akindele & LeMay, 2006; Berhe, 2009).
Unlike early efforts of individual tree and stand volume estimations which follow destructive method, recent research works use allometric equations constructed from easily measurable tree parameters, mainly diameter at breast height (Dbh) and total height (H) (Yohannes, 2002; Akindele & LeMay, 2006; Zhao et al., 2016). Allometric equations are the cost-effective methods of estimating the economic and ecological values of both natural and plantation forests (Lehtonen et al., 2004; Kebede & Soromessa, 2018). Moreover, both volume and biomass data are the principal input to predict the status of forest and designing appropriate silvicultural interference (Fox, 2000; Gregoire & Köhl, 2000; Foli et al., 2003; Ezenwenyi et al., 2018). The other merits of using allometric equations are their ability to reflect the actual estimation of total carbon and biomass of the stand including the un-merchantable components of the forests, particularly trees (Gómez-García et al., 2014). Reliable information about total tree volume and biomass is fundamental input to assess site productivity, carbon sequestration and overall sustainability of an ecosystem (Djomo et al., 2010). Total tree volume and aboveground biomass equations are recently considered as the central objectives of forest inventory, carbon stock monitoring and management plans (Brandeis et al., 2006; Subasinghe, 2008). In addition to the diameter at breast height and total tree height, some allometric equations employ form factor to estimate total stem volume; however, inclusion of form factor has less practical advantage (Yohannes, 2002; Hjelm, 2011). Thus, the common expression of tree volume as a function of diameter at breast height (outside bark) and tree height was used for this study (Mugasha et al., 2016).
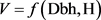 (1)
(1)
where: V = Total volume, Dbh = Diameter at breast height and H = Total height.
To date, estimations of aboveground biomass especially tropical forests have received much attention and considered as a principal component of forest management (Brown, 2002; Chave et al., 2005; Yitebitu et al., 2010). As a result, many researchers use different approaches to estimate the biomass accumulated in a given forest. Apart from allometric equations and direct measurement, conversion of national inventory data to aboveground biomass is possible through the two distinctive approaches (Chave et al., 2013). The first approach used for species with known merchantable volume is through application of simple models employing biomass expansion factors (Brown, 2002). However, the high dependency of BEF on species growth characteristics and lack of timely updated data in most tropical countries national forest inventory are the two bottlenecks of using biomass expansion factor (Brown, 2002; Dutcă et al., 2010). The second and more general approach of estimating aboveground biomass from national inventory data obtained from satellites, remote sensing, aerial photography is normalized difference vegetation index (NDVI) (Van Breugel et al., 2011; Günlü et al., 2014). Biomass estimation using NDVI is relatively less accurate, subjective and biased (Brown, 2002; Dutcă et al., 2010). BEF is expressed as:
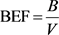 (2)
(2)
where: B = Aboveground biomass (dry weight), V = Total volume.
It is noteworthy that the use of allometric biomass regression equations is time and resources efficient method to estimate the biomass accumulated in large-scale industrial plantations (Delitti et al., 2006; Somogyi et al., 2008). There is no universally accepted allometric equation to estimate volume and biomass of trees; thus, allometric equations used for different species and sites are not the same (Berhe, 2009; Worku & Soromessa, 2015). Mixed species tree biomass regression models is applicable for most diverse tropical forests, however, the results of mixed regression models are less accurate and hardly represent all species in the forest (Chave et al., 2005). Therefore, species specific allometric equations can better estimate the volume and biomass of a given plantation species and other species of similar growth characteristics (Worku & Soromessa, 2015).
Plantation forests constitute a significant share of forest resources cover and sequestered considerable amount of carbon in Ethiopia (Yitebitu et al., 2010). Though quantification of volume and biomass of forest plantations is vital; previous attempts to develop tree volume and biomass allometric for plantation species in Ethiopia (especially indigenous trees species) are inadequate (Henry et al., 2010; Tesfaye et al., 2016). Like many indigenous trees there is lack of predictive allometric equation for the total volume and aboveground biomass of J. procera plantations in Wondo genet, Sidama Zone, Southern Nations, Nationalities and Peoples' Region, Ethiopia. Development species specific allometric equations is crucial in view of the fact that reliable information, precise quantification and projection of stand level total volume and aboveground biomass in the study site and other places with similar agro-ecological and species types are important. Therefore, focus of the paper is to develop and select best fit total volume and aboveground biomass allometric equations and estimating the biomass expansion factor for J. procera plantations in Wondo genet.
2. Materials and Methods
2.1. Species Description
Juniperus procera is naturally found in the central highlands of Ethiopia, mainly between altitudes of 2300 - 3200 m a s l, with an annual rainfall range that varies between 450 and 1200 millimetres (Couralet et al., 1992). It is an indigenous conifer species found in Ethiopia It is locally named as “Tid” and commercially known as “African Pencil Cedar” (Berhe & Negash, 1998). This tree has been a very important source of wood for timber and fuel with minimum demand on land (Gibbs et al., 2007). Its wood is fragrant, fine in texture with strait grain and highly resistant to termites as well as fungal diseases. Because of these distinctive qualities, it is considered as one of the high quality wood for construction of houses, internal structures of churches, furniture and for poles (Couralet et al., 1992). It is an evergreen deciduous, more seldom monoecious tree, which belongs to the family of Cupressaceae and genus Juniperus. It is the tallest juniper tree in the world with two developmental phases, the juvenile and the adult stage (Gibbs et al., 2007). On the adult stage it is characterized by distinctive trunk and crown shapes extend up to 45 m height (Couralet et al., 1992; Berhe & Negash, 1998). It has male and female cones, male cones are small and round; while the female cones are berry-like rounded that becomes fleshy upon ripening (Carreiras et al., 2017). This tree’s flower and give fruits produces 40,000 - 50,000 seed per kilogram (kg) with germination rate of 20% - 70% throughout the year without an interrupting resting stage (Gibbs et al., 2007).
2.2. Site Description and Stand Selection
Samples were collected from plantation sites on July 2018 from southeast of Shashemene, Wondo Genet, Southern Ethiopia. It is located in 7˚13'N and 38˚37'E, about 263 Km south of Addis Ababa and 13 Km east of Shashemene, at an altitude of 1800 - 2100 m. The study site is characterized by a bimodal pattern of precipitation with an annual average of 1200 mm, where a short rainfall period runs from March to April with a long rainfall period covers from June to September and a dry period extends from December to February. The study area is one of the most productive agricultural lands in Ethiopia with a good access to irrigation water supply from the upper catchments and ideal temperature ranging from 19˚C - 25˚C. It is known for the production of cash crops such as Saccharum officinarum, Coffea arabica and Cata eduli’s and natural and plantation forests. To simplify the sampling procedure, a management plan and map of the plantation were used as a tool to locate each compartment and compiled the history of the compartments. The management plan provided all the required site information about the available species in the plantation area. Accordingly, Cupressus lusitanica, Eucalyptus citriodora, Eucalyptus grandis, Grevillea robusta, J. procera, Pinus patula, Pinus radiate, Podocarpuse falcatus and others are among the dominant tree species. J. procera covers about 7.6% of the total plantation area, which makes it the widely growing indigenous tree species in the study area.
2.3. Data Collection
2.3.1. Tree Volume Data
Sample trees for volume estimation were taken from all diameter classes after the diameter distribution of each stand has recorded from a 5.64-meter radius circular plots laid using systematic random sampling (Mugasha et al., 2016). Diameter at breast height measurements from 69 sample plots to determine the Dbh distribution of the across all compartments and grouped into 10 diameter classes in way to accommodate the variability of tree diameter (Worku & Soromessa, 2015). Altogether, one hundred ten sample trees from all diameter classes were selected and felled for further measurements. Diameter at breast height, stamp height (0.2 m), 0.35 m, 0.5 m, 0.65 m, 0.8 m and 1 m were measured before felling. To get sufficiently reliable data the diameter over bark at a one-meter interval from Dbh to the top of the tree and total height were measured after felling using Caliper and meter tape respectively (Berhe, 2009). Diameter records were taken by cross-calipering along the axis of the tree bole. The total tree and log volume between consecutive diameter measures was calculated using Smalian’s formula, while cone formula was used to compute the top stem section volume.
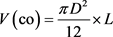 (3)
(3)
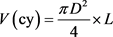 (4)
(4)
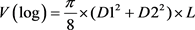 (5)
(5)
The Dbh distribution, frequency and the sample trees felled for tree volume estimation are presented in Table 1. While the minimum, maximum, mean and standard deviation values for total volume, Dbh and tree height are depicted in Table 2.
![]()
Table 1. Frequency and diameter class of sample trees for biomass data.
where: Dbh = diameter at breast height, H = total height, Sd = standard deviation, min = minimum, max = maximum, Sd. = standard deviation, Vi = individual tree volume.
2.3.2. Tree Biomass Data
Fifty-one of the total one hundred felled sample trees for volume were considered for biomass measurement. Nearly five sample trees from each compartment were considered for biomass. Following similar procedure to tree volume samples, the diameter over bark and total height of the tree was measured and sub-divided into three components stem, branch, and foliage. Then, three sub-samples were taken from each respective tree components. The total green weight of stems, branches, and foliage components was determined directly in the field using beam balance of 100 kg capacity. The field fresh weights of all components were summed up to obtain aboveground fresh weight of each tree. The minimum, mean and maximum fresh weights of the stem were 36, 85.25 and 137 kg respectively. While the minimum, mean and maximum values were 6, 31 and 56 kg for branch and, 5.5, 13.5 and 23 kg for leaf samples respectively. The frequency distribution of the sample trees taken for biomass models are summarized in Figure 1.
To determine the dry weight of the trees, representative sub-samples were taken from the dissected tree components (stem, branches, and foliage) were taken to laboratory for dry weight determination. Accordingly, three stem disc sub-samples were taken from stump height at 20 cm, Dbh (1.3 m) and 50% (half) of
![]()
Figure 1. Distribution of diameter at breast height of sample trees for biomass data.
the total stem length. Finally, a total of 153 stem sub-samples were taken for determination of stem dry weight and moisture. Branch samples were grouped into three classes (small, medium and large) by size. One branch disc was taken from the live crown of each branch group. A total of 153 branch sub samples (discs) were taken for further measurements. For foliage samples, overall 102 foliage sub-samples were taken for laboratory dry-weight analysis. After immediate labelling and coding with respect to component, sub-samples of each component were sealed in plastic bags, and taken to a laboratory for weight measurement. Fresh weight of sub-sample component was uniformly weighed with electrical digital scale balance (with a precision of +−/0.1 g), and liable to air drying for approximately 7 days (Gibbs et al., 2007). The stem and branch discs were oven dried at 105˚C, while leaf samples are oven dried at 70˚C until constant weight has recorded. The summary of dry to fresh weight ratio of sub-samples is given in Table 3.
2.4. Model Selection and Evaluation
Considering the essential role of allometric equations in predicting the total volume, biomass, evaluating the ability of sinking atmospheric carbon dioxide (CO2) and greenhouses, several research works have been published and applied for centuries (Fox, 2000; Chave et al., 2005; Gibbs et al., 2007). Validation of tree volume and biomass equations were essential in predicting the forest dynamics, socio-economic values, global trends of climate change and estimation of carbon sequestration (Ribeiro et al., 2011; Carreiras et al., 2017). Both total tree volume and models biomass regression equations use diameter at breast height and total tree height to predict the aboveground biomass accumulated in a given forest (Dutcă, 2018). Measurement of independent variables used to predict tree volume and biomass should be free measurement error, however error free measurement of variables is hardly practicable and might lead to under or
![]()
Table 3. Summary of dry to fresh weights ratio of sub-samples.
over estimation of the dependent variables (Arias-Rodil et al., 2018). Thus, dealing with the best predictive equations in a way to minimise the measurement errors is highly advisable. Though total tree volume and aboveground biomass equations are several and are site and species specific, we analysed the most frequent and possibly most predictive allometric equations used by previous researchers ( Vieira et al., 2008; Table 4).
Comparison of the regression models were carried out by using statistical values computed directly from entire data sets (Kozak & Kozak, 2003). Statistics such as bias (B), standard error of estimates (SEE), an average absolute value of the error (ABE) and estimated coefficient of determination (R2) are the commonly applied statistics to evaluate the model performance and select the best fit equations (Segura & Kanninen, 2005; Lumbres et al., 2011). Other literature also employed B, SEE, R2, AB and SD as performance evaluation for taper models (Berhe, 2009; Ezenwenyi et al., 2018) and above- and belowground biomass of selected species (Kalita et al., 2015). Similarly, the performance the selected models fitted to volume and biomass data in this study was evaluated using those four commonly used performance statistics: bias (B), standard error of estimates (SEE), mean absolute value of the error (MAE) and estimated coefficient of determination (R2). All the performance statistics used are defined below.
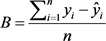 (6)
(6)
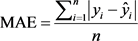 (7)
(7)
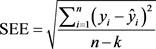 (8)
(8)
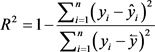 (9)
(9)
where: 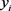 = observed response variable value,
= observed response variable value, 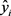 = estimated response variable value,
= estimated response variable value,  = mean value of response variable, n = number of observation, i = number of estimated parameters, n = number of trees, k = number of estimated parameters.
= mean value of response variable, n = number of observation, i = number of estimated parameters, n = number of trees, k = number of estimated parameters.
Total tree volume and aboveground biomass equations with highest coefficient of determination (R2) value, lowest bias, SE and MAE were selected as
![]()
Table 4. Total volume and aboveground biomass equations.
where: Vt = stem volume in m3, B = aboveground biomass, H = total height Dbh = diameter at breast height and α, β1, β2, β3, β4 and β5 = model parameters.
best-fit models. After ranking of each performance statistics for all allometric equations, the final ranking was accomplished by summing up the ranks for the four computed performance statistics. Equations with lower sum of ranks were selected as best fit allometric models to predict the total volume and biomass models (Berhe, 2009).
2.5. Data Analysis
All computations and analysis for this study were carried out using IBM SPSS statistics version 20. The linear and none-linear models listed in above were fitted to estimating total volume and aboveground biomass using the linear and multiple regression equations at a significance level of 0.05.
3. Result and Discussion
The result and discussion part of this paper presents findings of the research with respect to the designed research objectives. Therefore, this part includes an estimated total stand and individual tree volume and aboveground biomass, fitting of models for estimating volume, of aboveground biomass, comparing biomass estimates computed from developed biomass model for J. procera and the computed biomass expansion factor.
3.1. Total Volume
The initial stage of analysing and actual processing of data for developing the best fit total volume models, the graphical illustration of the relationship between total tree volume and potential predictors of the one hundred ten sample trees was constructed in Figure 2. The results indicated that, total tree volume relates differently to different expression ways of the potential predictors like diameter at breast height and total tree heights. Accordingly, the results presented in the graphs below the total volume of sample trees showed weakly linear relationship with total tree height (H) and (H2), while it showed a fairly positive correlation with diameter at breast height (Dbh), Dbh2. The total tree volume has shown a strong linear relationship with Dbh × H, Dbh2 × H, H2 × Dbh and (Dbh × H)2. Dbh2 × H appeared to be an appropriate predictor for reducing heterogeneity and stabilizing error during volume estimation. The results revealed that considering Dbh has a greater effect on prediction of total tree volume, thus, considering the variability of Dbh in fitting volume models is crucial. Similar conclusion has been drawn for the tropical rain forest of Nigeria (Akindele & LeMay, 2006).
Fitted Volume Models
Six allometric equations considered to compare their ability to estimate total tree volume and their respective parameters of estimates are presented in Table 5. Following computing, the parameter of estimates, bias (B), standard error of
![]()
Figure 2. Scatter plot of total volume versus potential predictors.
![]()
Table 5. Volume model performance statistics and their rank in parenthesis.
estimates (SE), mean absolute error (MAE) and coefficient of determination (R2) for all candidate models were ranked according to their performance of each computed statistics and their ability to estimate the total tree volume. Final rank of the compared models was determined by summing up the performance of each model with respect to the chosen statistical measures at p-value = 0.05.
According to the above results, all of the allometric volume equations are highly significant at an alpha level of 0.05 with explaining potential of ≥88% total volume variation; the obtained results were similar to the research result presented from urban trees in the north-eastern USA (Troxel et al., 2013). The last column of Table 5 shows the rank of the models. Previous studies ascertained that allometric equations are specific to species and site; however, models with less bias, high coefficient of determination, less standard error and mean square error are best estimator models (Chave et al., 2005; Cole & Ewel, 2006; Berhe, 2009). Accordingly, model six (6) followed by model five (5) yields the smallest sum of the ranks, hence; model six (6) outperforms the rest of the models and selected as the best total volume models. To clearly identify the performance of models having equal variances standardized residual were plotted against the predicted volume (Akindele & LeMay, 2006). The standardized residual versus fitted volume scatter plot; estimated from both the least squares method and generalized least squares method indicate even distribution of observations. The results obtained for this study in lines with the remarks given by other works (Berhe, 2009; Kozak & Kozak, 2003). Particularly, the estimated and residual volume of Cupressus lusitanica and Pinus patula plantations in Ethiopia using model two (2) was clearly presented by (Berhe, 2009). The observed against estimated volume constructed for this study is presented in Figure 3.
3.2. Aboveground Biomass
3.2.1. Descriptive Analysis
The ratio of oven dry weights to field fresh weights of the tree components (stem, root, braches and leaves) employed to estimate the total biomass of trees
![]()
Figure 3. The scattered plot for estimated and observed total tree volume.
were computed. Hereafter, the total aboveground biomass was obtained by summing the stem, branch and leaf dry weights (Ounban et al., 2016). To validate the aboveground biomass allometric equations, the relationships between tree dry weights and potential predicting parameters were evaluated. The results displayed in Figure 4 indicated that aboveground biomass exhibits nonlinear relationship with H and H2. However, aboveground biomass exhibits a strong linear and linear relationship with Dbh and Dbh2, respectively at a 95% confidence intervals; this result in line with the research result presented by (Delitti et al., 2006; Van Breugel et al., 2011; Ounban et al., 2016). A significant increase in biomass accumulation was observed with increasing diameter of the trees.
The proportion of aboveground biomass varies with tree components (stem, branches, and foliage) Figure 5. The mean proportion of aboveground biomass by tree component was estimated to be 50.1% (foliage), 47.4% (branch) and 45.5% (stem). The overall average dry to fresh-weight ratio was approximately 45.7%. The dry to fresh-weight ratio approximately estimated to be 47.7%. The average dry to fresh-weight ratio was higher for foliage than the branch and stem components.
According to previous research works, belowground biomass of trees estimated to be approximately one-fifth (20%) of the aboveground biomass (Pearson et al., 2005; Giri et al., 2014). Thus, predicting the belowground biomass (BGB) from the aboveground biomass is more time and resource saving approach (Worku & Soromessa, 2015). Therefore the belowground biomass in was estimated as follows:
![]() (10)
(10)
where: BGB = belowground biomass, ABG = aboveground biomass.
3.2.2. Fitted Biomass Models
Even though there are a lot of biomass equations used to estimate below and aboveground components of plants, few allometric equations used by (Zianis & Mencuccini, 2004; Mulat & Soromessa, 2016) are the commonly used models to
![]()
Figure 4. Relationship of aboveground biomass and potential predictors.
![]()
Figure 5. Proportion of aboveground biomass tree components.
estimate biomass of different tree components stem, branch, leaf, and root. Though, Zianis and Mencuccini (2004) stated that site fertility, elevation, soil type diameter at breast height and total tree height are some of the common variables used in fitting biomass estimation equations, only diameter at breast height and height were applied in this study. Thus, six commonly used models applied and developed by (Zianis & Mencuccini, 2004; Chave et al., 2005; Zianis et al., 2005; Siregar, 2011; Brown, 2015) were employed for this study. The fitted biomass models and their parameter estimates are presented in Table 6.
Similar to the procedures followed in fitting volume models, the four performance statistics were computed for biomass models. Results displayed in Table 6 indicated that all the allometric equations used can well determine the aboveground biomass accumulated in the forest stands. Moreover, the SE and MAE values of all models are close in their values, indicating of the competitive performance of the biomass models. According to the sum of computed performance statistics displayed on the last row of Table 6; model one (1) followed by model three (3) was found as the best models to estimate the aboveground biomass of J. procera plantation. Worku and Soromessa (2015) have also applied similar evaluation statistics to select best-fit models to estimate the biomass and carbon accumulated in Podocarpus falcatus in Wof-Washa forest, Ethiopia. These researchers finally conclude that allometric equations are species specific. Generally, applying biomass equations has a big contribution in improving the reliability data on national carbon inventories at a single species level or large scale plantations of similar nature (Jalkanen et al., 2005).
3.2.3. Biomass Expansion Factor
Measurement of total tree volume from diameter and total tree height is more direct and easier than determination of biomass. The use of biomass expansion factor which is the ratio of total biomass mega gram (Mg) to total volume (m3) is a useful approach to convert the total tree volume accumulated in a given forest stands to biomass (Zhao et al., 2016). There is a possibility of using previously developed BEF by other researcher, however the value obtained are mostly biased due to variability of estimated volume and biomass with species and site (Zhao et al., 2016). Once species specific total volume and biomass models have selected, the expanding stem biomass to whole tree and total biomass accumulated in the forest stands and large-scale plantations forests (Dutcă et al., 2010). Forest inventory data obtained from national and local management plans are the inputs used to calculate the accumulated forest biomass by employing the BEF for each plots. Thus, prediction of biomass is an easy task in a condition total tree volume data is available. In this study, the selected aboveground biomass model one (1) and volume model six (6) were used to estimate biomass and volume of trees obtained from 69 circular plots of 100 m2 area laid across the plantation stands of the J. procera plantation. The estimated BEF, total volume (V) and biomass (B) per hectare are presented in Table 7.
The estimated BEF in this study was approximately similar to the 0.84 for Spruce, 0.74 for Pine and 0.99 for broadleaved dominated stands in Norway (Viken et al., 2012), 0.71 for Scots pine stands, 0.81 for Norway spruce stands spruce and 0.64 for broad-leaved stands based on the Sweden’s National Forest (Viken et al., 2012). However, the result of this study was inconsistent with the results of BEF of 2.1 ± 1.0 reported for different agroforestry species in subtropical
![]()
Table 6. Fitted aboveground biomass models.
![]()
Table 7. Biomass expansion factor, estimates total volume and aboveground biomass of J. procera plantation in the study area.
region of Yassica Sur district (Segura et al., 2006) and 1.6 ± 0.2 for tropical humid forest in Costa Rica (Segura & Kanninen, 2005). The variation in the BEF obtained in this study has strengthen the argument about BEF is site and species dependent. The predicted belowground biomass was approximately 15.5455 mega gram per hectare (Mg/ha).
4. Conclusion and Recommendation
Results of this study indicated the possible application of allometric equations for prediction of total volume and aboveground biomass of plantations. In particular case, total volume model Vt = b1 + b2Db3Hb4 and aboveground biomass model B = β1Dbhb2Hβ3 were selected as the best fitted equations to estimate the total volume and aboveground biomass of J. procera plantation. These selected models provide consistent estimations and logical relationships of Dbh and H with the total volume and aboveground biomass. The obtained results also revealed models selected for biomass estimation of both total volume and biomass were different from the previously used equation to estimate in other place and other species, which revealed the inconsistency of models with species and site. These models are believed to be applied by different organisations such as national carbon monitoring centre and academicians to estimate the total volume and biomass of the J. procera and species of similar nature in and out of the study site. As the values estimated by BEF and direct measurements are much closer to each other, application of BEF for AGB estimation without destructing trees is thought to be the best alternative option. This doesn’t mean that validation of equations and BEF with local data is not required. Though tapper and canopy cover models are equally important, the financial and time limitations limited this study to address them. Therefore, future studies should address these gaps. Finally, the researcher would like to suggest that difficulties associated with forest inventory could be minimized; if such models are developed for all other highly valuable indigenous tree species in Ethiopia.
Acknowledgements
The author is grateful to Wondo Genet College of Forestry for financial support and allowing us to cut trees for data collection from their plantation, carrying out laboratory measurements and other facilities including transportation during field data collection.