Star Formation in Magnetized, Turbulent and Rotating Molecular Cloud: The Critical Mass ()
1. Introduction
Star formation is one of the most important and yet unsolved problems of astrophysics. It plays an important role in many different areas of astrophysics, especially in the field of galaxy formation and evolution [1] . Without a theory of star formation, it will be difficult to understand the origin of galaxies and luminous matter in our universe. Molecular cloud is a cool dense interstellar region composed of a wide variety of molecules, mainly hydrogen, plus some dust, in which stars are forming. Cores are the denser sites of star formation in molecular clouds with number density
[2] . A star forms as the final stage of various complexes, non-linear dissipative processes that are the result of the interplay between turbulent, thermal and magnetic pressure effects on one side and gravity on the other side [3] . However, how star formation is triggered and inhabited by pressures supporting gravity and opposing gravity needs a detail theoretical formulation by incorporating magnetic tension.
The standard theory simply related to the magnetic fields of the progenitor main-sequence stars frozen during collapse or flux conservation [4] . This model does not deliver the mechanism how magnetic field supports and opposes gravity in star formation. Understanding the origin and evolution as well as physical behaviour of the complex process of star formation (SF) is still an ongoing research area in modern astrophysics. Solving those problems will help to develop a theory regarding origin of stars. Some of unanswered questions regarding the role of magnetic fields in star formation are: What is the effect of magnetic fields on MC core collapse? It has been suggested that magnetic fields suppress fragmentation [5] . The other way suggested is that the presence of magnetic fields may enhance fragmentation [6] . To this end, we perform theoretical formulation how magnetic field counteracts gravity and how mag- netic tension supports gravity in a gravitating, magnetized turbulent rotating MCc.
The first numerical calculations of the collapse of a molecular cloud core to stellar-core formation and beyond was performed by [7] . Where as [8] combined the radiation hydrodynamical (RHD) method of [9] and the magnetohydro- dynamical method of [10] and performed the first smoothed particle radiation magnetohydrodynamic (SPRMHD) calculations of protostellar collapse to stellar- core formation. In this paper, we combine energies due to gravity opposing pressures and energies of gravity supporting pressures to formulate the critical mass of gravitating, magnetized, turbulent and rotating MC core in the presence of magnetic tension effect. Thus we show how those pressures counteract and support gravity in dispersing and collapsing MC core respectively.
Clouds do not become gravitationally bound, and they dissipate; those that are self-gravitating form stars in essentially a free-fall time [11] [12] . But what if the cloud is strongly magnetized? This needs additional theoretical formulation to understand how magnetic pressure, with turbulence and rotation controls star formation. It is also necessary to describe how the size of the core influences magnetic pressure and magnetic tension. In other case it has been explained that supersonic turbulence will dissipate on roughly the free-fall time scale as collapse of gravitationally bound clouds [13] [14] . Although magnetic pressure cannot stop the collapse [15] [16] . Strong magnetic pressure together with supersonic turbulence in large scale and pressure due to rotation can dominate gravity and elongate the SF time. Therefore, we intend to explain how magnetic tension supports gravity in collapsing the MCc. The general purpose of the study is: Theoretically to formulate the critical mass of gravitating, magnetized, turbulent and rotating MCc in the presence of restoring force due to magnetic tension.
2. Basic Equations and Approximations
In the process of star formation different energy pressures are involving in collapsing as well as holding the cloud. As an initial condition we assume gravitating, magnetized, turbulent and rotating molecular cloud. Some energies are supporting gravity and some are opposing gravity during star forming process. The energies involved in star formation are originated from, gravity, magnetic field, turbulence, rotation, thermal effect as well as external pressures. For the MC initially in force balance, the combination of these energies is written as
(1)
where
is the total gravitational energy,
is the total thermal energy,
is the total magnetic energy (If B inside is greater than out side),
is energy due to the magnetic tension,
energy due to turbulent motion,
is rotational energy, and
is the external pressure, and V is the total volume. The sum of gravitational energy, energy due to magnetic tension and energy of external pressure must exceed the sum of all pressures counteracting gravity for the MCc to collapse. Thus Equation (1) is re-written as
(2)
The coefficient 2 for total kinetic energy (where
) shows half of the gravitational energy goes to total kinetic energy during MC collapse. In this process tremendous amount of gravitational energy is released and taken away via mechanisms of energy transport. The gravitational energy released raises temperature of the core and kinematics of the particles in the gas cloud. Half the gravitational energy is released in the form of radiation and half of it rises temperature, kinematics and tend the cloud to rotate. Thus rotation also plays its own role in supporting the cloud core as well as determining critical mass of the cloud. In this paper we do not consider external pressure because the source of external pressure is violent explosions like supernova, which we can not specify its equation for the time being. Therefore we focus on energies or pressures, which we can formulate their equations. Since gravitational energy released when a MC of mass M and radius R collapses is given by
(3)
where
is gravitational constant for spherical cloud. In the same manner rotational energy is written as
(4)
where M is mass of the rotating cloud core, R is its radius,
is its angular velocity and
is rotational constant. In this study we assume angular
velocity that depends on mass distribution. In other way turbulent energy of the cloud of mass M with turbulent velocity dispersion is given by
(5)
where
is three-dimensional velocity dispersion given by
(6)
In this study we consider isotropic velocity dispersion, hence for isotropic velocity dispersion
, where
is the radial velocity dispersion and it is the only one we can measure (the other two are perpendicular to our line of sight). Therefore
(7)
whereas the known equation of thermal energy is written as
(8)
Now neglecting external pressure from Equation (2) and using Equations (3), (4), (5) & (8) we rewrite Equation (2) as
(9)
where
is the Boltzmann constant, T is temperature of the cloud,
and
are atomic mass unit and mean molecular weight of the gas in atomic mass unit.
Magnetic Pressure & Magnetic Tension
One of the most fundamental questions in astrophysics is how do stars form [17] . Observations clearly show that this process takes place in self-gravitating, turbulent, magnetized filamentary molecular clouds (for more clarification see [18] ). However, the question of how magnetic tension supports gravity in collapsing MCc is still largely unanswered. In gravitating, magnetized, turbulent and rotating MC core some energies are counteracting gravity and some are supporting gravity (such as magnetic tension and external pressure). In this study we mainly focus on magnetic tension than external pressure. Equations of those energies can be obtained from their corresponding pressures. Where magnetic pressure is given by
(10)
Magnetic energy is volume integral of magnetic pressure, so that
(11)
Integrating Equation (9) over the volume of sphere of MC core leads to
(12)
This is if the field inside the cloud is much larger than the field outside it. Magnetic field B can be the initial field (seed field) from galaxy. Hence the core inherits magnetic field from its parental MC or clump, thus we consider conservation of magnetic flux. Assuming the total flux threading a given area is a conserved quantity, then
(13)
where
and
are the magnetic field and radius of the initial or parent cloud which is not yet collapsed; where as
is the new magnetic field strength after the sphere of cloud has been compressed slightly to radius R. Thus
(14)
Inserting Equation (14) in Equation (12) we have
(15)
In actual fact there is an extra term of the same magnitude for the magnetic field strength between R and
[19] , so that the magnetic energy is
(16)
Assuming radius of curvature of the magnetic field line extends over the core radius. Therefore,finally magnetic energy of a molecular cloud of radius
collapsing to a cloud core of
is written as
(17)
We apply this equation (Equation (17)) for our next work. On the other hand, there is a magnetic curvature force pointing toward its center of curvature; there is a restoring force called magnetic tension force, which is caused by magnetic field lines extended over a given radius of curvature and is given by
(18)
Magnetic tension is the restoring force due to magnetic field line over its radius of curvature. Then magnetic tension acts to straighten bent magnetic field lines. To obtain magnetic energy due to its tension we integrate Equation (18) over the radius dr of the spherical cloud core as
(19)
We assume the radius of curvature of the magnetic field line extends over the cloud core radius (
in our expression). Thus we have
(20)
Using conservation of flux, and thus inserting Equation (14) in Equation (20) we have
(21)
As cloud core collapses from radius
to R the field strength increases so that, we assume, there is an extra magnetic tension term of the same magnitude for the magnetic tension between R and
. Therefore, energy due to magnetic tension, which is directed towards centre of curvature of B is redefined as
(22)
This is energy due to magnetic tension over a given radius of curvature which supports gravitational energy in collapsing MC core and dilutes magnetic pressure as much as possible. If
has larger radius of curvature than B, therefore,
has larger restoring force due to tension. This energy acts to straighten bent magnetic field lines, simultaneously it enhances the inflow of matter. So that, it is important in collapsing molecular cloud to form star. This is why we define magnetic tension is a gravity supporting force in star formation.
3. Results & Discussions
The Critical Mass
Critical mass of the molecular cloud is the minimum amount of mass needed by the cloud to collapse and form star. In this section we formulate the critical mass of gravitating, turbulent, magnetized and rotating molecular cloud core by incorporating magnetic tension. Now plugging Equations (17) and (22) in Equation (9) we have
(23)
where
&
are the mass and radius of the collapsing cloud core respectively. From Equation (23) we have
(24)
Multiplying both sides of Equation (24) by
and considering spherical core of mass
as well as substituting
we arrive at
(25)
Simplifying the last two terms we have
(26)
Dividing both sides of Equation (26) by
and taking out
from the last terms we arrive at
(27)
We assume isotropic turbulent velocity dispersion
, which is given by
, hence for isotropic velocity dispersion
, where
is the radial velocity dispersion the only one we can measure (the other two are perpendicular to our line of sight). Thus Equation (27) becomes
(28)
Now substituting
(29)
By rearranging Equation (29) we get
(30)
Hence the gas pressure from equation of state is given by
(31)
where
is particle number density of the core,
is the Boltzmann constant and
is core temperature. Then, using Equation (31) we have
(32)
The core can collapse & form the star if the condition in Equation (32) satisfied. But it expands if
(33)
Finally, the critical mass of gravitating, magnetized, turbulent, and rotating star-forming molecular cloud core in the presence of magnetic tension is formulated as
(34)
where
is the critical mass of magnetized MC core. The core mass has to exceed this critical mass to collapse and form star. Equation (34) is the critical core mass explained in general way. Recent studies show average values of the magnetic field of molecular cloud is »5 - 15 μG [20] [21] . We use the average of this magnetic field in our calculation. Since angular speed of molecular cloud is approximated to 10−15 s−1 - 10−13 s−1. For instance, given a pre-stellar core of initially collapsing MC (parent cloud) rotating with
, depends on mass distribution,
,
,
is radius of parent MC ~ 1pc,
, typical MC magnetic field
, speed of sound
, assuming supersonic turbulent velocity dispersion
, we find the critical mass of this MC is ~
, beyond this mass the MC core becomes supercritical. Due to this reason the cloud core collapses and can form star. This confirms that properties of the parent cloud governs the critical mass of molecular cloud core. The role of rotation is displayed in Figure 1 when the core rotates rapidly the cloud supporting pressures increase, so that the cloud must contain large mass within small size to collapse. The critical mass is lower at
in Figure 1, it may be the minimum critical mass required in order to collapse for the MCc under consideration. Above this radius it needs larger MCc mass to collapse and form star. We understand that from Figure 2 outflow from the core disperses gases and dusts near to the surface of the protostar. At this stage stellar wind also made the circumstellar disk to disperse. Far away from the core those dispersed
![]()
Figure 1. The pre-stellar core radius vs its relative critical mass (
). With parent MC radius
,
,
,
,
, and
. The figure shows high angular velocity results in larger critical mass. This figure is plotted making use of Equation (34). This figure shows to overcome the pressure of rotation the MCc mass has to be relatively larger to collapse.
![]()
Figure 2. When magnetic field lines stretched over its radius of curvature. Here, the protostar grows to pre-main sequence star. Simulated using vertical structure and disk radius where
is the angle between the horizontal and core’s gravity (g), where as
is the vertical component of the core’s gravity. Dipolar magnetic field line equation is used to simulate the field lines. This figure is just to show the importance of magnetic tension how it holds the central core and its envelope together.
materials condense and coagulate. A strong stellar wind breaks out at the rotational poles, reversing the infall and producing bipolar outflows. This phase is connected with the disk formation phase. Then after the newly formed star/disk system becomes optically visible and the protostar is identified as a T Tauri star or Low mass (
) young stellar objects (YSOs) [22] [23] .
Magnetic field line extends out of the central protostar radius this helps to hold the protoplanetary disc and the central stellar object (see Figure 2). Therefore, if there is strong magnetic tension the disc may not escape from the star and has great chance to form planets. Of course the strength and geometry of magnetic fields implanted in protostars during the star formation process is unknown [8] . However, we use dipolar field lines for simplicity, and to show how magnetic tension is playing a crucial role in star formation. As the protostar collapses and rotates the field lines are twisted into helical shapes. Then drawing the field lines closer together results in strong field and the twisting of the field causes torsional Alfve’n waves to travel along the field lines, like torsional waves on a string. The magnetic field is responsible for carrying away excess angular momentum by being tied to the surrounding envelope. We show in Figure 3 & Figure 4 the minimum critical mass is
in the presence of all possible energies in our model (Equation (34)) for those specified conditions. If there is no magnetic tension the minimum critical mass is beyond the value we get here, i.e.
.
4. Critical Mass in Different Cases
In this section, we consider different cases to see how conditions can vary the critical mass of a star-forming MCc. In our assumptions, the initial condition for
sound speed in MCc is
[24] and the supersonic turbulent velocity dispersion is greater than 332 m∙s−1.
If the core is very large in size the ratio of
approaches to zero. So that
![]()
Figure 3. The pre-stellar core radius vs its relative critical mass (
). Assuming parent MC radius
,
,
,
,
, and
. The red solid line is for the magnetized parent cloud core whereas the black broken line is for unmagnetized MC core. The figure is plotted from Equation (34) (the red curve) and Equation (36) (the black broken line).
we omit the last term of Equation (34) in parenthesis. It is almost approaches to zero ( ) and has no significant effect unless the core radius is too small. Due to this reason Equation (34) becomes
) and has no significant effect unless the core radius is too small. Due to this reason Equation (34) becomes
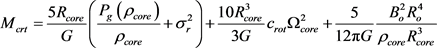 (35)
(35)
If a core is very large in size its critical mass can be calculated using Equation (35). This kind of core has to be denser and massive to collapse.
This condition is for unmagnetized MC if it exists. Or when the influence of magnetic pressure and tension is insignificant. Thus Equation (34) becomes
 (36)
(36)
A non-magnetized cloud core’s critical mass depends mainly on density, radius and angular speed. If the core is denser, small in size and slow rotating it can collapse, even if it has small mass according to Equation (36).
If magnetized turbulent cloud core is not rotating . Then its critical mass is expressed as
. Then its critical mass is expressed as
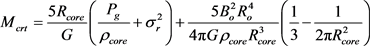 (37)
(37)
This situation describes a non-rotating cloud core’s critical mass. Here the role of magnetic tension is significant to protect the cloud from dispersing.
This condition explains where there is a probability of getting non-turbulent and non-rotating, but magnetized and gravitating molecular cloud core. For this case Equation (34) becomes
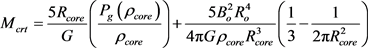 (38)
(38)
In this case gravity left alone to trigger MC to collapse. For this condition Equation (34) becomes
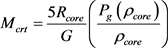 (39)
(39)
From both cases (case I to case V) we clearly understand that star formation process depends on varies parameters and physical conditions in addition to magnetic tension. Therefore, understanding factors affecting critical mass of the MCc will provide some idea for star formation theory. In this paper, we formulated five different equations of critical mass from the basic model (Equation (34)). Then those equations are useful to calculate the critical mass of star-forming cloud core. In rare case if there are no gravity opposing pressures the minimum critical mass we obtained is 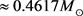 (shown by the black line in Figure 7). These show how critical mass of star-forming MC depends on different dynamical process and conditions. However, the minimum critical mass contained in different radius of the core is quite different from one another regardless of having the same
(shown by the black line in Figure 7). These show how critical mass of star-forming MC depends on different dynamical process and conditions. However, the minimum critical mass contained in different radius of the core is quite different from one another regardless of having the same  and
and . This means that there is a specified critical mass for each radius of the core (example see Figures 4-7).
. This means that there is a specified critical mass for each radius of the core (example see Figures 4-7).
The blue curve in Figure 7 indicates near the center of the core magnetic pressure is extremely high, so that the cloud has to be massive and more dense to collapse. But as radius the increases the corresponding critical mass reduces,
because as the radius of curvature increases magnetic tension increases. The point at which the blue and red curves cross each other is the point (radius) at which magnetic field effect is equal to the effect of turbulence plus rotation. At the same time, the red line shows as radius increases critical mass also slightly increases, and the curve has positive slope, this tells us no magnetic tension as B = 0. Therefore, gravity struggles alone to bring matter from the envelope to the central core. Thus the black line in Figure 7 shows the only dominating energy is gravitational energy, due to this the graph attains positive slope and the smallest critical mass at smaller radius than other cases.
The blue curve in Figure 7 confirms how strong magnetic pressure is near the center of the core and being diluted by magnetic tension plus gravity at a point far from the center. Fortunately if the cloud is not magnetized but rotating and turbulent, we obtain the graph of radius versus critical mass with positive slope (see red curve in Figure 7). As indicated in Figure 8 a highly supersonic turbulent cloud core has to contain very large mass within a small radius to collapse, but this small radius can not hold the amount of masses indicated by the black dashed line in this figure, which is out of reality, therefore, magnetized and highly supersonic cloud may not collapse before cloud life time. However, it seems realistic for subsonic turbulence i.e. indicated by the red line in this figure. For dense regions in cold molecular clouds of![]() ,
, ![]() and
and ![]() it has been found that the initial core mass
it has been found that the initial core mass ![]() [25] . However, turbulence and rotation were not considered by [25] in his particular finding. Nevertheless, we interpret our findings using simple energy balance equations by incorporating gravity, thermal, rotation, turbulence, magnetic pressure and magnetic tension. In Table 1 different critical masses have been displayed because all possible pressures except external pressure have been incorporated in our model (Equation (34)), and then critical masses are calculated for different conditions (as shown in Table 1).
[25] . However, turbulence and rotation were not considered by [25] in his particular finding. Nevertheless, we interpret our findings using simple energy balance equations by incorporating gravity, thermal, rotation, turbulence, magnetic pressure and magnetic tension. In Table 1 different critical masses have been displayed because all possible pressures except external pressure have been incorporated in our model (Equation (34)), and then critical masses are calculated for different conditions (as shown in Table 1).
Numerical Results of Magnetic Field from Literature for Comparison
Magnetic fields of the line of sight for OMC B (Orion molecular cloud B) and CMC (California molecular cloud) has been measured using rotation measure data from the literature [26] . The Orion molecular cloud (OMC) is a well-studied, active star-forming region. CMC is also a giant molecular cloud, but with relatively little star formation activity. This indicates the combination of
those parameters we have been used in Equation (34) is very important to determine the minimum cloud core mass required for collapse. Since CMC has lower density than Orion [26] For this reason, magnetic pressure dominates gravity plus magnetic tension, this made CMC has lower star formation rate than OMC. Therefore, our model will help to describe why some giant molecular clouds are not active in forming star. Despite their similarity in size and mass, Some molecular clouds are characterized by rates of star formation that differ by more than an order of magnitude [27] . So that our results more securely establish that significant variations in the level of star formation activity and star formation rate are common in magnetized molecular clouds and are dependent on the cloud core magnetic field strength. As a result, it is possible from comparative studies of such clouds to determine the physical factors that govern the star formation rates in molecular clods.
The negative and positive signs in Figure 9 & Figure 10 indicate magnetic field directed away from the observer and magnetic field toward the observer respectively. This comparison is just to see how critical mass depends on dynamical process & parameters including magnetic field. Thus our result has its own contribution in building star formation theory. Even so, the author ( [26] )
![]()
Figure 9. Line of sight (LOS) magnetic field of OMC B (Orion molecular cloud B) versus Rotation measure of Molecular Cloud (RMmc) J2000. RMmc is the rotation measure of the molecular cloud alone as described in literatures [26] . The graph is plotted using data available online and obtained from J/A + A/614/A100 [26] . Green circles indicate the magnitude of magnetic field of the cloud at its corresponding rotation measure.
![]()
Figure 10. Line of sight (LOS) magnetic field of CMC (California molecular cloud) versus Rotation measure of Molecular Cloud (RMmc) J2000. The graph is plotted using data available online and obtained from J/A + A/614/A100 [26] . RMmc is the rotation measure of the molecular cloud alone. Blue circles indicate the magnitude of magnetic field of the cloud at its corresponding rotation measure.
did not calculate the critical mass of those molecular clouds with respect to their magnetic field strength. Rather they measured magnetic fields of the line of sight using rotation measure data.
5. Conclusions
Star formation in magnetized, turbulent and rotating MC may take longer time unless magnetic tension supports gravity. The minimum core mass required to collapse, and form star can be calculated for different conditions. Indeed, the model indicates magnetic tension has also its own role in protecting cloud dissipation. If the role of magnetic tension is negligible, the core would take longer time than cloud life time to collapse, which results in non-star-forming region. In other way, for the case of no magnetic tension, turbulence has to decay before the free fall time, then the core collapses in time to form star. This implies there is a competition between turbulence and magnetic tension. Our findings confirm that the interplay among many dynamical processes made too difficult to fix the critical mass, unless we know the properties of the environment in which the star-forming cloud resides. Recent observations confirmed that there are non-star-forming giant molecular clouds. Therefore, our model displays some reasons to answer the question why some clouds do not form star through identifying the role of magnetic pressure and tension of magnetic field lines.
Strong magnetic pressure causes dissipation of the cloud through ambipolar diffusion (slow drift of neutral particles across magnetic field lines) and forbidding the infall of matter from the envelope. In addition, rotation also supports magnetic pressure, the faster the envelope rotates around central core the more difficult for the core to gain mass. We have shown to what extent each energy pressure determines the critical mass of star-forming MC core (see Figures 2-8 and Table 1). These figures indicate how magnetic pressure is too strong at relatively inner radius of the core, and results in the necessity of larger critical mass for MCc to collapse and form star. In Figure 7, we show magnetic tension has significant role in supporting gravity at a point far from the center of the core. Thus at a great distance from the center of the core, magnetic pressure is diluted by the sum of magnetic tension and gravity. This is why the blue curve and black line overlap in Figure 7 at ![]() for this particular situation. In general, we model critical mass of star-forming molecular cloud core in different cases by involving magnetic tension at the beginning. According to our view, where there is magnetic field in star-forming cloud core there is also unavoidable magnetic tension.
for this particular situation. In general, we model critical mass of star-forming molecular cloud core in different cases by involving magnetic tension at the beginning. According to our view, where there is magnetic field in star-forming cloud core there is also unavoidable magnetic tension.
Acknowledgements
We thank Ethiopia Space Science and Technology Institute (ESSTI), Entoto Observatory and Research Center (EORC) for providing this research oppor- tunity. Our gratitude also goes to International Science Programme (ISP) for supporting this study. We also acknowledge with thanks the anonymous reviewers for their constructive comments as well as [26] for making their data publicly available online for scientific community. G.M. Kumssa, thanks Jimma University for permitting study leave.