An Inexpensive and Simple Experimental Approach for the Estimation of Solute Import into Groundwater and Subsequent Export Using Inflow/Outflow Data ()
1. Introduction
In water balance models, solute import/export at different scales ranging from point measurement to catchment scale in space over-time into and out from groundwater (GW) is usually linked to inflows into and outflows from aquifers [1] - [8] . Of particular importance with regard to point measurement, outflow and solute export are GW-head [3] , temperature-time series [7] , and recharge an discharge [5] . However, these workers have indicated that model outputs may be less reliable, particularly in situations where the information in the aforementioned major variables listed in [1] - [8] is scarce. Furthermore, reliable information in GW inflow/outflow is particularly important in situations where GW base flow discharges contribute substantially towards the total annual flow in streams, carrying nutrient contaminants such as N and P, and pesticides discharge the flows into sensitive surface water bodies (SWB) [4] - [11] .
Nitrate export from GW under intensively cultivated agricultural catchments in northeast humid tropics of Queensland, Australia, and the subsequent loading in SWB, particularly the UN listed World Heritage Great Barrier Reef (GBR), is a major aquatic ecosystem health hazard/risk [12] [13] in this region. The export in surface runoff from agricultural catchments to the GBR has been fairly well documented but that from the GW base flow discharge has received limited attention [12] [13] . The limitations are partially attributed to the complexities involved in characterizing and quantifying GW inflow/outflow from point measurement extrapolated to larger scale and over-time [3] [6] [7] [8] [9] . Coupling GW inflow/outflow with solute import/export spatiotemporally may help to at least partially resolve the issues mentioned above, however, to my knowledge, such coupling information is scarce.
Conceptually, there are two approaches to experimentally quantify GW inflow/outflow and link it with solute import/export. Logically and intuitively the most appropriate would be to quantify each and every component of GW inflow/outflow and solute import/export processes, listed as major variables controlling these processes in [1] - [8] , to increase the confidence level. Briefly, the major variables to quantify the inflow/outflow are the vertical, both upward and downward, and lateral discharge of GW and solutes, solute adsorption/desorp- tion, mineralization/degradation/decomposition reactions, solute (nutrient) uptake by crops and recycling, regolith dissolution and atmospheric deposition. This approach is too expensive, laborious, and time consuming to undertake simultaneously to address all the issues at field scale, and to my knowledge, such information based on experimental data from a single study is scarce to nil. Alternately, the changes in watertable levels between consecutive monitoring, implying between a given inflow and the outflow that immediately follows the inflow, and the corresponding changes in solute concentrations (import/export) may be considered as an approximation to account for the aforementioned bio- physical-chemical processes/reactions outlined in the first approach. This approach is relatively simple, low-tech and cost effective, compared with the first approach, while not jeopardizing the accuracy and reliability. Therefore, this study is based on the second approach, where the specific objectives are to assess the temporal dynamics of (i) rain water inflow/outflow behaviour in three contiguous agricultural catchments in the humid tropics of far-northeast Queensland of Australia, (ii) solute import via inflow and subsequent export in outflow, and (iii) the association between GW inflow/outflow and solute import/export.
2. Materials and Methods
2.1. Study Catchment
2.1.1. Johnstone River Catchment
The Johnstone River Catchment (JRC) is approximately 1634 km2 in area and is located between 17˚30'S and 145˚50'E in northeast Queensland, Australia (Figure 1). Pristine rainforest covers ≈ 50% of the mountains and hills of the catchment, pasture 28% (both dairy and beef) at midslopes, 12% sugarcane and 8% banana at the lower aspects in landscape [12] [13] . The major rivers in the catchment are the North and South Johnstone Rivers, both of which rise in the south-eastern section at 740 m elevation, pass through large areas of native rainforest in the midsection of the catchment and drain the undulating lowlands and floodplain of the lower catchment. The rivers converge in an estuary in Innisfail which discharges water into the Great Barrier Reef.
The basaltic regolith in the catchment is highly weathered and stratified contiguously, and ranges in thickness from 50 to 120 m [14] . The stratification can lead to complex subsurface flow paths, but this aspect has received little research attention. The topography is generally undulating and the GW flow generally follows the topography and surface drainage features [14] . Water transmissivity in the basalts can range from 17 to 3500 m2/d and values greater than 500 m2/d are often associated with vesicular basalt or highly weathered scoria aquifers [14] . The major cultivated soil types belong to the Ferrosols soil order [15] [16] as did the soil at the study site. The Ferrosols profiles are deep, red to brown, acidic, well-structured clay soils and include the soil series formed in-situ (Pin Gin and those formed on from alluvium derived from basalt). The saturated hydraulic conductivity in the top 0 - 0.1 m is relatively high, ranging from 5.1 m/d to 17.1 m/d, and is 0.14 m/d to 0.27 m/d at a depth of between 0.5 and 1.0 m [14] .
2.1.2. Mulgrave River Catchment
The Mulgrave River Catchment (MRC) is located between 17˚01' and 17˚24'S and between 145˚37' and 145˚58'E, covering an area of 1983 km2 in north east Queensland, Australia (Figure 1). Approximately 12% of the catchment is under intensively cultivated sugarcane, 3% grazing, 17% timber reserve, and 57% in the
![]()
![]()
![]()
Figure 1. The location of the study sites in the three catchments.
Wet Tropics World Heritage Area [17] . The major river in the catchment is Mulgrave River.
The regolith in this catchment is mostly quaternary alluvium resulting from hundreds of thousands of years of sedimentary depositions [14] [15] [17] . The deposits vary in thickness from 45 m to 100 m with coarser sands generally located between 15 m and 45 m below the surface. At the study site, the top 12 m regolith is vertically stratified showing varying mixtures of clay/silt/sand at 0 - 4 m depth and mostly mottled clay at depths > 4 m. The lateral stratification from up-to down-slope ranged from clay/silt/sand mix to gravel/sand mix. Published information on sub-surface soil hydraulic properties are scarce to nil, except for the unpublished work of [14] who reported the cumulative percolation during rainy season can be greater than 700 mm/yr.
The majority of soils under sugarcane in MRC, including that at the experimental site, are alluvial acidic drystrophic brown dermosol characterized by 43% - 44% clay, 30% - 32% silt, 23% - 24% sand, in the top 0.20 m [9] [14] . The pH of these soils in the top 0.1 m was 5.4, 0.6 mg/kg organic C, and 1.9 cmolc/kg cation exchange capacity.
2.1.3. Tully River Catchment
The Tully River Catchment (TRC) is located between 17˚30'S and 18˚30'S latitude and at 14˚6'E longitude, covering an area of 1683 km2 in northeast Queensland of Australia (Figure 1). The major river systems in the catchment are the Tully River and Murray River which discharge into the GBR lagoon. The topography ranges from precipitous mountains to depositional plains [18] . Approximately 20% - 23% of the total area is under agricultural activities.
The cultivated soils in this catchment were formed in-situ from the metamorphic parent rocks that form the mountains in this area. The hydro-geologi- cal information is very scarce for this catchment [18] . The soil type at the experimental site is brown Dermosol, characterised by high clay content, ranging from 62% to 68%, and the clay mineral is predominantly 1:1 kaolinite [18] . Only one soil of basaltic origin has been mapped out so far, although many of the fans are of mixed basaltic granitic origin.
2.2. Groundwater Monitoring and Sampling
2.2.1. Piezometer Wells
The piezometer wells (simply the “wells”) used in this study to monitor watertable levels and water sampling in the three catchments were installed in mid- 1990’s to early-mid-2000 for other studies. In the JRC they were installed along a ≈380 m long transect at up- , mid- and down-slope positions. The downslope wells were approximately 25 m away from the nearby creek. At the MRC the wells were installed in a similar fashion along a 650 m transect, where the downslope wells were ≈40 m away from the nearby creek. The wells in the TRC were arranged in a triangular fashion at ≈50 m apart and the nearest stream was the main field drain, draining ≈300 ha of banana crop, ≈1 km away from the wells.
Soil boreholes (96 mm diameter.), ranging in depth from 5 m to 20 m were drilled using a hydraulic rig. After coring, PVC pipes (43 mm internal diameter.) with tightly sealed bases were inserted into the boreholes and grouted to serve as piezometer wells. Prior to insertion a segment of each pipe was slotted and wrapped with 250 mm seamless polyester filter socks to facilitate water inflow into the wells but prevented coarse sand particles from entering the wells. A 0.15 m thick bentonite collar was placed just above the slotted portion of the pipe to prevent water entry from above the collar. Above this collar, the space between the pipe and bore-wall was tightly back-filled with sand and soil material to 6 m below the soil surface and the top 6 m section of the space was filled with cement and approximately 1 m of the pipe was left above the soil surface and this was covered with a lockable cap. The watertable levels reported in the text are the depth to GW from soil surface.
The upslope well in JRC was 10.7 m deep, that in MRC 12 m, and in TRC 11 m deep, respectively. Even though there were nested wells installed to different depths in JRC and MRC, such nested arrangement was not in place in TRC. Therefore for simplicity and consistency the results from the aforementioned upslope wells will only be reported in this paper.
2.2.2. Watertable Monitoring and Sampling
The depth to groundwater (DGW) measurements and water sampling were conducted at 7 to 10 day intervals from January through May (rainy season) commencing in 2003 to 2005 in JRC, 2004 to 2006 in TRC, and 2007 to 2009 in MRC. Monitoring and sampling were scheduled to occur 12 to 24 hr after major rainfall events, and after dry-spells that lasted between two consecutive rainfall events. The former provided information on rising GW (inflow) and the latter on receding GW (outflow). The DGW was measured using a special noise trigger tape and water samples were collected following the procedures described in [19] for solute analysis. The samples were kept at approximately 4˚C upon arrival in the laboratories and analyzed for nitrate-N, chloride, and electrical conductivity (EC) using the procedure described by [20] .
2.2.3. Rainfall
The climate in the northeast humid tropics of Australia is characterized by a very humid summer rainy season and mild dry winter. The summer rainy season (mid-December through to mid-May) is generally characterized very high rainfall. The long-term average rainfall in the JRC is ≈2353 mm, 1600 mm in MRC, and 2670 in TRC. More than 75% of the total annual rainfall is received during the rainy season and downpours as high as 200 mm∙d−1 are not uncommon [14] . The daily rainfall data during the investigation period was recorded in automated weather stations located at 1 km, 3 km, and 5 km away (aerial distance) from the wells, respectively at MRC, JRC, and TRC (Table 1). The estimated pan-evaporation rarely exceeds rainfall during the rainy season, but irrigation may be required for some horticultural crops from July to November.
![]()
Table 1. Average monthly rainfall distribution (short-term) during the rainy season in the three catchments compared with the long-term averages and the totals.
2.3. Cropping and Fertilizer History
The experimental sites at MRC and JRC were under native rainforest before being deforested for cultivation in the early 1950’s, and after deforestation it has been under intensive sugarcane crop production systems until now. Before the mid 1980’s a trash-burn sugarcane production system was in operation, this changed to a green-blanket system which is being continued until now in MRC and JRC. At TRC a similar sugarcane production was in operation until 1990 and this changed to banana production until now. The N-fertiliser input for banana at TRC during the study period ranged from 310 to 525 kg N/ha.yr as urea and/or diammonium phosphate and muriate of potash at 400 to 500 kg/ha∙yr The N-fertiliser was split applied (with between 8 and 20 applications annually). The N-fertiliser applications during the dry months (July-November) were fertigated. At MRC and JRC the N-fertiliser input during the study period ranged from 100 to 120 kg N/ha.yr as urea or diammonium phosphate. It was applied once at planting in June-August or for the ratoon crop and another dressing in December before the onset of rainy-season.
2.4. Statistical Analysis
We chose the descriptive parameters mean, standard error, minimum, maximum, and the coefficient of variation (CV) to statistically characterize the temporal changes in watertable levels and solute concentrations within and between rainy seasons [21] [22] . Simple linear regression analysis was performed to determine the associations between variables. The [23] software package was used for the statistical analysis of the data.
2.5. Computation of Cumulative Inflow/Outflow, Recharge/Discharge, Cumulative Nitrate Import/Export
In this paper the difference between the depth to watertable from ground surface before a given rainfall event (X in m) and that immediately following it (Y in m) is considered as the inflow depth = 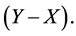 (1)
(1)
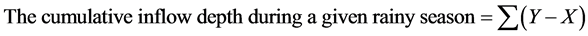 (2)
(2)
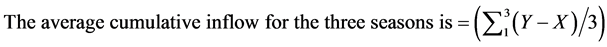 (3)
(3)
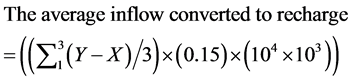 (4)
(4)
In Equation (4), 0.15 is the freely drainable porosity [24] , and the recharge is in L/ha.
Similarly, the outflow depth in meters is the difference between the depth to watertable from ground surface after a given rainfall event (P in m) and that before the subsequent rainfall event (Q in m) = 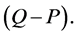 (5)
(5)
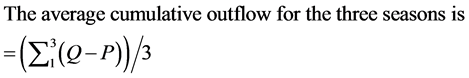 (6)
(6)
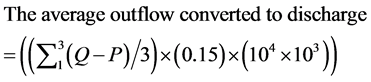 (7)
(7)
In Equation (7), 0.15 is the freely drainable porosity, and the recharge is in L/ha.
Nitrate import after a given inflow event is the difference between the concentrations after and before the inflow = M ug/L. (8)
Nitrate export is the difference between the concentration after a given rainfall and that before the next rainfall event = N ug/L. (9)
 (10)
(10)
 (11)
(11)
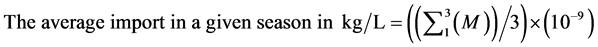 (12)
(12)
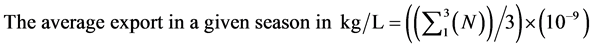 (13)
(13)
The average import in given season in kg/ha = Equation (12) ´ Equation (4) (14).
The average export in given season in kg/ha = Equation (13) ´ Equation (7) (15).
3. Results and Discussion
3.1. Rainfall and Watertable
The influence of the rainfall received during the monitoring periods on watertable fluctuations in the three catchments shown in Figure 2, indicate the watertable rose in response to the rainfall received beginning in January, receded between rainfall events, fluctuated temporally throughout rainy season, rapidly receded in May/June, and thereafter gradually receded to levels that existed before it began to rise again in January. The behaviour of the temporal fluctuations were simular across the catchments. For example, in JRC it rose from 9.82 m
![]()
Figure 2. The groundwater table fluctuations during the rainy season in the three catchments.
below the surface during the first week in January 2004 to 4.96 m in late March, then receded to 6.78 m in early April, and rose again to 4.27 m, and thereafter it began to recede continuously to 9.45 m in early November (Figure 2). In between the aforementioned periods there were temporal fluctuations, and similar trends were observed during the 2003 and 2005 rainy seasons and in the other two catchments also (Figure 2). However, magnitude of the GW rise or decline for similar rainfall events varied between the catchments, suggesting temporal fluctuations were overrided by site-specific system variable impact (Figure 2). Detailed discussions on the spatiotemporal changes in watertable fluctuations in the three catchments as impacted by rainfall distributions for the same rainy seasons as in this paper have been already been reported in [9] [10] [11] , therefore in this paper the emphasis will on inflow/outflow.
3.2. Groundwater Inflow/Outflow
3.2.1. Johnstone River Catchment (JRC)
The inflow and outflow depths of water shown in Figure 3, show they varied temporally within and between seasons, but depended on site-specific system variable impact across the catchments. The extent of variations are statistically characterised by the ranges (min-max), CVs, and means (Table 2). The inflow depths after rainfall events ranged from 0.07 to 3.12 m with a mean of 1.29 m. The extent of the variations in the ranges are characterised by a CV of 78%. The primary dynamic variable that controlled this variation was rainfall distribution (Figure 3 and Table 2). The outflow depths between rainfall events ranged from 0.14 to 1.41 m with a CV of 51% and a mean value of 0.72 m. The CVs indicate the in flows showed larger variations than the outflows. The primary dynamic variable that controlled the outflow variations was the number of days between two consecutive rainfall events. The cumulative inflow depth (length of the profile that was filled with rain-water) for the three seasons was 15.52 m and the corresponding cumulative outflow (length of profile that drained through freely drainable porosity) depth 13.68 m. The average inflow depth per season and the corresponding outflow depth were 5.17 m and 4.56 m, respectively. Using these seasonal inflow and outflow depths the profile recharge and the discharge were computed and they are 0.776 m and 0.684 m, respectively (see materials and methods for the computational details). This recharge quantity is similar to what [14] for the tropical catchments. The average recharge was ~42% of the of the three year average, short-term, rainfall (Table 1). The short-term average rainfall was ~526 mm less than the long-term average, implying the cumulative inflow depth could have been greater than 15.52 m.
The discharge was ~37% of the short-term average rainfall. Other workers have shown the annual surface runoff in the humid tropics could range from 35% to 40% of the rainfall [14] [25] [26] . These imply that surface runoff was approximately equal to baseflow discharge, suggesting the importance of the latter with regard to pesticide and nutrient, if any present in GW, export to streams and also the environmental flow requirement during dry season, June to De-
![]()
Figure 3. Inflow into and outflow from shallow groundwater tables in the three catchments.
![]()
Table 2. A summary statistics for means, minimum and maximum (min-max), and coefficient of variation (CV) for depth to groundwater, nitrate-N, chloride, and electrical conductivity in the piezometer wells in the Johnstone River (JRC), Mulgrave River (MRC), and Tully River Catchments (TRC). The electrical conductivity measured in μS∙cm−1 is converted to mg/L using a division conversion factor of ~2 found in conversion tables for better perception.
cember. The runoff plus the GW discharge during a given rainy season could be 70% to 80% of the rainfall.
It is very likely that preferential bypass vertical flow through macropores, fissures and cracks, the variations in geologic stratigraphy, hill-slope downward flow, along with piston matrix flow might have also contributed towards the cumulative inflow and outflow observed in this catchment [27] [28] [29] [30] [31] . At this stage the proportional contribution by each one of the aforementioned contributors toward total inflow is not known and the quantification of the proportional contribution is beyond the scope of this study. Therefore, it is highly probable the inflows and outflows are approximation of the integrated impact of the aforementioned system variables. Thus, the watertable method of inflow/outflow computation, approach 2 in this study, may help to increase the accuracy of water-balance model outputs rather than resorting to complex mathematical manipulations without sufficient field data to justify the accuracy of balances.
3.2.2. Mulgrave River Catchment (MRC)
The inflow/outflow data for MRC, north of JRC, shown in Figure 3, show the temporal behaviour was qualitatively similar to that observed at JRC. The inflow depths ranged from 0.03 to 3.54 m with a CV of 113% and mean of 0.98 m. The larger CV (113%) in MRC than JRC (781%), indicate the temporal changes were more rapid in MRC, than in JRC (Table 2). The outflow depths ranged from 0.01 to 1.85 m with a CV of 112% and a mean of 0.35 m, the larger CV in MRC than JRC again indicate the outflow occurred more rapidly in the former than in the latter catchments.
The cumulative inflow and the corresponding outflow depths for the three seasons in MRC were 19.41 m and 11.21 m, respectively. These imply the average seasonal inflow and outflow depths are 6.47 m and 3.74 m, respectively, and they produced 0.971 m and 0.561 m as recharge and discharge, respectively. The recharge and discharge in MRC were 43% and 25%, respectively, of the average short-term rainfall, compared with 42% and 37% in the JRC. The average discharge in MRC is less than that in JRC even though the average recharges were similar. The low discharge in MRC than JRC, suggest the differences in system variable impact between the catchments. The larger left-over recharge may help to prolong GW discharge during dry seasons, thereby meeting the environmental flow requirement during dry season.
The short-term average rainfall in JRC was ~526 mm less than the long-term average, whistle an opposite trend was observed in MRC where the short-term average rainfall was ~627 mm more than the corresponding long-term average (Table 1). The long-term average rainfall trends for the two catchments indicate the seasonal inflow depth in MRC could be less than 0.971 m whereas that in JRC it could be higher than 1.29 m. The importance of the impact of long-term average compared with the short-term average indicates the need for caution in expressing generalised statements, inferences, and conclusions with regard to the effect of rainfall on inflow/outflow.
3.2.3. Tully River Catchment
The inflow/outflow data for the TRC shown in Figure 3, show the temporal behaviour is qualitatively similar to that observed in JRC and MRC. The inflow depths ranged from 0.07 to 1.83 m with a CV of 81% and a mean of 0.74 m, these ranges are less than those obtained for JRC or MRC (Table 2). The outflow depths ranged from 0.04 to 1.15 m with a CV of 112% and a mean of 0.41 m which is also less than that of JRC, 0.81 m, and marginally higher than MRC’s 0.35 m. The cumulative inflow and outflow depths in TR were 17.46 m and 17.03 m, respectively, with seasonal average inflow and outflow as 5.82 m and 5.69 m, respectively. The average inflow and outflow indicate the average recharge and discharge were 0.873 m and 0.854 m, respectively. The average recharge and discharges were ~34% and 33%, respectively, of the short-term average rainfall. The recharge and discharge in TRC were less than the corresponding recharges and discharges in JRC or MRC. Even though the seasonal average rainfall, both short-and long-term, was higher in TRC and than in JRC or MRC, the lower recharge and discharge are attributed to the differences in system variable impact between the catchments, particularly fewer macropores linked to high clay content ranging from 62% to 68% in TRC compared with 28% to 32 % in JRC and 42% to 44% in MRC.
3.3. Solute Import/Export Dynamics in Groundwater
The data shown in Figure 4 for nitrate, chloride and the electrical conductivity (EC) for the three catchments show the import into and the export of the solutes from GW varied spatiotemporally within and between rainy seasons across the catchments. For example, the imported nitrate concentration temporally varied
![]()
Figure 4. Temporal changes in nitrate, chloride, and total dissolved solutes (electrical conductivity) import/export in the three catchments.
from 0 to 1470 µg/L in the JRC compared with 13 to 561 µg/L in MRC and 8 to 2439 µg/L in TRC with mean values of 561 µg/L, 158 µg/L, and 767 µg/L, respectively, for the three catchments. The temporal variations are characterised by the large CV values of 86% for JRC, 122% for MRC, and 101% for TRC. The mean values indicate the highest import occurred in TRC followed by JRC, and MRC. Higher N-fertiliser input of 310 to 525 kg N/ha∙yr in TRC compared with 100 to 120 kg N/ha∙yr in JRC or MRC is the primary reason for the higher import in TRC than JRC or MRC.
The simple correlation between nitrate import and inflow indicate the imports were strongly correlated with inflow in JRC and MRC catchments as indicated by R2 values of 0.75 and 0.84 (Table 3). Even though the correlation was significant for TRC, the import was controlled by 49% of the inflow compared with 75% to 84% in the other two catchments. The gross differences are attributed partially to the differences in system variable impact between the catchments as indicated in the inflow/outflow.
The exported nitrate concentration in JRC ranged from 200 to 1670 µg/L
![]()
Table 3. Simple correlation analysis summary for nitrate, chloride, total dissolved solutes, and inflow and outflow.
All possible correlations were performed and only those that were found significant are reported in the table. The superscript “a” denotes significant at P < 0.10 and the others significant at P < 0.05. The best fits were forced through zero, assuming no import/export if there were no inflow/outflow.
compared with 24 to 401 µg/L in MRC, and from 50 to 2412 µg/L in TRC. The exported ranges show qualitatively similar trends to the import, implying varied spatiotemporally. The ranges are characterised by CV values of 73% for JRC, 72% for MRC, and 94% for TRC. However, these CVs are less than the corresponding CVs obtained for the import, suggesting less rapid temporal changes in export than import. The average export from JRC was 723 µg/L compared with 128 µg/L in MRC and 761 µg/L in TRC. The correlations between nitrate export and outflow indicate 77% of the export in JRC was accounted for by outflow compared with 44% in MRC and 49% in TRC (Table 3). The gross differences are attributed partially to the differences in system variable impact between the catchments as indicated in the inflow/outflow.
The average seasonal import and export for each one of the three catchments and the corresponding average recharge and discharge are used to compute the average seasonal import and export as described in the materials and methods section and listed in Table 2. The average import in JRC was 25.3 kg/ha compared with 10.5 kg/ha in MRC and 33.8 kg/ha in TRC. The corresponding exports were 24.5 kg/ha, 7.5 kg/ha, and 26.3 kg/ha in JRC, MRC, and TRC, respectively. It seems that ~97% off the imported nitrate was exported in the outflows of JRC compared with 72% in MRC and 78% in TRC. The highest import in TRC is attributed to the largest N-fertilizer input, as much as thrice as that in MRC and JRC. Even though the fertilizer-N inputs were similar in JRC and MRC, the lesser import in the latter cannot be attributed to seasonal rainfall differences as it was higher, by ~407 mm, in the MRC than JRC (Table 1). The higher import in JRC than MRC is attributed partially to the favourable system variable impact, the presence of fissures and cracks in the basaltic regolith that facilitated more rapid bypass flow of rain-water than through the alluvium of MRC. It seems that major proportion, 72% to 97%, of the leached out nitrate was exported during the rainy season itself. This suggests the discharge and the corresponding export should be included in the total loads transported in the streams that discharge into sensitive surface water bodies (SWB) in the humid tropics. However, it should be noted the discharged baseflow and the nitrate in it are only that exited the well. The discharge to reach and mix with stream flow depends primarily on the half-life of nitrate [32] and the transit velocity [33] . Furthermore, the import vs. export balance of ~3% to ~27% may undergo adsorption in the basaltic JRC regolith [34] and mineralization reactions.
Chloride and electrical conductivity’s (EC) temporal dynamical behaviour are believed to be good indicators of GW flow directions [35] [36] , so this aspect in this paper is given due consideration to account for solute import into and export out of the GW wells. The large min-max ranges for Cl in the three catchments indicate the concentration varied rapidly over-time. The Cl import in JRC ranged from 0 to 3100 µg/L compared with 70 to 10,700 µg/L in MRC and 250 to 9510 µg/L in TRC with CVs of 82%, 140%, and 86%, respectively, for the three catchments (Figure 4 and Table 2). The mean imports were 1146 µg/L, 1994 µg/L, and 3128 µg/L, respectively for JRC, MRC, and TRC. The relatively high mean value for TRC is a reflection of the large quantity of KCl input for banana compared with moderate input to sugarcane in the other two catchments (See materials and methods). Chloride exports ranged from 100 to 3100 µg/L, 40 to 11,800 µg/L, and 500 to 22,374 µg/L in JRC, MRC, and TRC, respectively, with CVs of 81%, 128%, and 128% for the three catchments, suggesting rapid changes in Cl export qualitatively similar to their import cousins. The mean exports were 1325 µg/L, 2515 µg/L, and 3791 µg/L, respectively, in JRC, MRC, and TRC. The mean exports from the catchments were higher than the corresponding import by 16%, 26%, and 21%, respectively in JRC, MRC, and TRC. Higher export than import may be due to dissolution of regolith material for which there is no direct evidence to my knowledge.
The EC data shown in Figure 2 indicate they varied spatiotemporally as did the nitrate and Cl. The ECs’ were divided by a conversion factor of ~2 (http://www.chemiasoft.com/chemd/TDS) to obtain total dissolved solutes (TDS). The TDS import temporally varied from 0 to 13.2 mg/L in JRC compared with 1.0 to 23.8 mg/L in MRC and 0 to 65.2 mg/L in TRC (Table 2). The temporal variations are characterised by 93%, 241%, and 163% CVs for JRC, MRC, and TRC, respectively. The exports’ temporal variations are qualitatively similar to the corresponding imports. The exports ranged from 2.0 to 14.2 mg/L in JRC, 0.0 to 10.5 mg/L in MRC, and 0 to 62.5 mg/L in TRC, with corresponding CVs of 67%, 83%, and 156%, respectively. The CVs indicate the imports were more temporally dynamic than the corresponding exports. The average import in JRC was 6.4 mg/L compared with 4.01 mg/L in MRC mg/L, and 10.9 mg/L in TRC. The highest import in TRC, approximately 41% and 63% more than in JRC and MRC, respectively, is attributed to the larger KCl input to banana in TRC than for sugarcane in JRC and MRC. The TDS export in JRC was ~18% less than the corresponding import compared with ~23% less in MRC and ~25% in TRC.
A comparison of the CV’s for EC vs. Cl indicate that EC's temporal variations were more rapid than Cl both in the inflow an outflow across the three catchments, except for that in the outflow of TRC. This indicates that EC is better descriptor of GW flow directions than Cl. Even though [35] showed similar results with regard to EC as tracer in stream bed, they didn’t compare it with Cl. According to [36] Cl can also be used as a tracer, however, this study shows that EC is better than Cl to characterise inflow/outflow directions. Because EC determination is relatively low-tech and cost-effective than Cl, the study recommends the use of EC to characterise GW flow directions. This may indirectly help us to improve and trace the transport direction of nitrate.
A comparison of the CVs of EC across the catchments indicates the temporal fluctuations in the GW-inflow were most rapid in MRC followed by TRC and JRC, respectively, in that order. This trend is similar to the inflow temporal fluctuations across the catchments, even though the CV for inflow was less than the corresponding CV for EC. However, such consistent trend was not observed between the EC in the outflow and the corresponding outflow itself across the catchments, suggesting further clarification through future research.
The imported nitrate plus Cl means as a percent of the corresponding TDS import in JRC was ~27%, compared with 47% in MRC and 36% in TRC (Table 2). The exported nitrate plus Cl means as a percent of the corresponding TDS export was 39%, 85%, and 55%, respectively, in JRC, MRC, and TRC. It seems the major constituents in the imported TDS were nitrate and Cl. The imported nitrate plus Cl means as a fraction of the corresponding exported TDS in JRC was 32% compared with 69% in MRC, and 48% in TRC, implying the major analytes in the exported TDS were nitrate and Cl. This again indicates the usefulness/importance of EC determination to characterise GW flow direction, consequently the nitrate flow direction. The exported nitrate mean as a fraction of the corresponding exported TDS was 11% in JRC compared with 5% in MRC and 9% in TRC. Even though the proportion of the exported nitrate in TDS is low, the hazard/risk associated with its export to sensitive SWB is substantial. Future research in nitrate import/export should consider computing the proportion of it in TDS that can be used to develop pedotransfer functions to estimate nitrate in GW-inflow/outflow where only EC data is available.
3.4. Implications of Nitrate Export to Offsite Surface Water Bodies (SWB) Receiving Baseflow Discharges and the Unresolved Issues
There are two issues that need attention with regard to nitrate import into shallow GW. First, whether this water is being used in households and the second is what are implications of the GW outflow and the export of the nitrate in it to streams and subsequent loading in SWB that receive steam flows. In this paper the first issue, household use, will not be undertaken. The second issue is number one priority in the far-northeast wet-tropics of Australia in relation to the sustainable health of the UN listed World Heritage Great Barrier Reef (GBR) [12] [13] . Nutrients, particularly nitrate and phosphate, pesticides, and sediment loadings in the GBR has been linked, partially, to the deteriorating health of the reef, which brings in billions of international and national tourist dollars to the local economy [12] .
The results from this study show that large quantities of nitrate were imported from agricultural soils into GW after rainfall events and subsequently most of it exited when the GW receded. It is also known the receded GW, most of it, was discharged into streams as baseflow. It is however not known how long it will take for the receded GW, with the nitrate in it, to reach streams. This then raises a question as to how old is the GW that is being discharged into streams or whether the recently infiltrated rainfall is being discharged. If the GW discharged is old not that percolated recently, then the nitrate in it might have undergone several biogeochemical reactions, consequently the concentration might have decreased compared to what is was when the monitoring was undertaken after rainfall events [32] . Answers to all the aforementioned questions are beyond the scope of this study. However, the recent study in MRC [33] show the transit time (TT) required to travel 280 m by employing flux-theory was ~15 years compared with ~2.7 years obtained using watertable recession approach. Shorter TT implies insufficient opportunity for the nitrate to undergo substantial biogeochemical reactions under anaerobic condition, thereby increasing the potential for its transport to streams.
[37] reported that in humid environment with conducive soil transmission characteristics, the subsurface flow contributed substantially towards stream flow. However, the large difference obtained using different methods for the estimation of TT suggest the flow mechanism and pathways may be different. The recession approach accounted for the flow through macropore bypass flow, fissures and cracks, “soil-pipe flow” and stream “gaining-loosing”, and piston-flow [33] , hence these workers concluded the TT estimates obtained using this approach is more appropriate than the piston-flow based estimates in MRC and may be in the other two catchments. [3] [4] [6] [7] [8] reported that extrapolations from point measurement (piezometer wells) of solute transport to catchment scale should take into consideration the issues of sorption in soil matrix and half-life of solutes along the transport path, including the aforementioned complexities. These workers have also indicated solutes with moderate sorption and long half-life are most susceptible to transport within an year of import. They also reported that those with high potential for rapid transport showed large annual/seasonal variability (CV). The high CVs obtained in this study (Table 2) indicate that solutes were transported relatively fast in inflow/outflow via macropore bypass flow, piston-flow, “soil-pipe” flow, and “stream gaining-loosing”, and piston-flow conditions that existed in the three catchments. It seems that extrapolation of point-measurement of solute concentration to solute mass-flux can only be undertaken provided spatiotemporal variations in GW flow direction and velocities are known. The results from this study while supporting their claim show how best to address the issue.
While acknowledging the aforementioned complexities and difficulties involved in baseflow discharges into streams, we propose to relate the concentrations of the nitrate in GW with the trigger values proposed for different aquatic ecosystems sustainable health hazard/risk in this region. The trigger values provided for the oxides of N, which is predominantly nitrate-N, provided in Table 3.3.4 of the [38] National Water Quality Management strategy report are used in this section to relate the hazard/risk associated with the nitrate in GW when it reaches sensitive SWB. The trigger values for SWB ranged from 1 to 4 μg∙L−1 for offshore marine reef, 2 to 8 μg∙L−1 for inshore marine reef, 10 μg∙L−1 for lowland rivers, freshwater lakes, reservoirs and wetlands, and 30 μg∙L−1 for upland rivers and estuaries.
The lower quartiles (LQ) for nitrate-N in this study the ranged from 300 to 1500 μg∙L−1 with a LQ of 1500 μg∙L−1 in JRC, 23 to 476 μg∙L−1 with a LQ of 476 μg∙L−1 in MRC, and 1761 to 3285 μg∙L−1 with a LQ of 3285 μg∙L−1 in TRC. The LQ indicate that 75% of the nitrate concentration in GW is 2 to 3 orders of magnitude higher than the triggers proposed for most of the SWB (Table 2). The minimum in the LQ range is higher than the trigger values, suggesting the nitrate in GW is a hazard/risk to most of the surface aquatic system sustainable health. The hazard to turn into risk depends on the TT, the half-life of nitrate in GW, and dilution effect when baseflow reaches streams. The half-life of nitrate in GW could range from 1 to 3 years [33] this coupled with the TT of 3 years [14] suggest the potential for 75% of the nitrate in GW to be transported to nearby streams. However, the dilution effect is to be accounted for when the baseflow discharge mixes with the stream flow. Thus we suggest the nitrate in the GW in the three catchments is a hazard/risk to the SWB receiving baseflow discharges and it should be given due consideration in order to provide more reliable N- loading estimates to sensitive SWB.
4. Conclusions
The rapid temporal changes in shallow groundwater (GW) levels, in as short as 7 - 10 days interval, in three tropical humid catchments were induced by rainfall and the dry-spell that followed the rainfall event, respectively. It is therefore claimed rainfall and dry-spells events are the dynamic variables that controlled the rise and the subsequent decline in GW levels. Even though the temporal changes, the GW rise and decline were similar across the catchments, the magnitude of the changes was dissimilar across catchments. This indicated that site- specific geo-hydrology of the catchments, a system variable, over-ridded/modi- fied the impact of dynamic variable, rainfall/dry-spell. It is therefore claimed the GW fluctuations is controlled by both dynamic and system variables. Based on the GW fluctuating results from this study, it is claimed the fluctuating temporal behaviour would be similar in other humid tropical catchments globally. The rise in GW level rise in linked to rainfall inflow into the aquifer and the decline to lateral outflow to streams.
The average cumulative inflow per season across the catchments ranged from 35% to 42% of the seasonal average rainfall, 1827 to 2580 mm, indicating substantial proportion of the rainfall percolated into soil profiles. The average outflow across the catchments ranged from 36% to 56% of the inflow indicating the potential for solutes, N, P, and pesticides, imported via inflow to exit via outflow.
Very large proportion (72% to 96%) of the imported nitrate and TDS (75% to 82%) exited via outflow during the same rainy season provides evidence for the potential for transport of these to streams. The statistics indicate that inflow accounted for 75% to 84% of the nitrate import and the outflow for 44% to 77% of the export. However, the outflows to reach the streams depend on the transit time, adsorption/desorption and mineralization reactions on the pathway, and the half-life of nitrate. To our knowledge, these issues are not resolved yet and need further research.
The approach employed in this study involves less sophisticated techniques for GW monitoring, sample collection and less expensive laboratory procedures for nitrate analysis. Furthermore, this study shows the least expensive EC for monitoring and laboratory analysis can be used as a surrogate for nitrate dynamics in inflow/outflow of GW after further calibration and regression validation. It is the author’s opinion. This is a unique research and can be undertaken in similar environment, particularly in developing countries, as the approach is low-tech, cost effective with regard to laboratory analysis. Furthermore, it doesn’t involve complicated mathematical manipulations and modelling that are usually carried out without sufficient calibration and validation.
Acknowledgements
The author gratefully acknowledges the field and laboratory support provided by Messrs. Heiner, D.H., Dwyer, M.J., and Mss. Whiteing, T., and Rowan, D.E. and the internal review and editorial comments provided by Ms. Glynis Orr.