A Novel Approach Based on Reinforcement Learning for Finding Global Optimum ()
1. Introduction
If  is a function of decision variables, where
is a function of decision variables, where , S is the feasible search space and
, S is the feasible search space and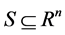 , an optimization problem can be defined as finding the value of
, an optimization problem can be defined as finding the value of  in S that makes
in S that makes 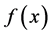 optimal for all x values. Despite the fact that different meta-heuristic algorithms have been improved especially in last two decades, the contributions of Reinforcement Learning (RL) to this area are still limited comparing to others. Numerous studies such as genetic algorithm based methods [1] [2] , ant colony based algorithms [3] [4] , harmony search approach [5] , modified firefly algorithm [6] and hybrid heuristic methods [7] [8] [9] have been proposed to optimize any given mathematical function. Apart from these applications, there are some attempts for solving engineering problems in different fields using RL based algorithms in the relevant literature. Hsieh and Su [10] developed Q-learning based optimization algorithm for solving economic dispatch problem after they tested their proposed algorithm for optimizing standard mathematical test functions. Their results showed that the proposed algorithm outperformed many existing optimization algorithms. Similarly, Samma et al. [11] tested newly developed RL based Memetic Particle Swarm Optimization algorithm on mathematical functions and real-world benchmark problems. Numerical examples applied indicated that the proposed algorithm is able to produce better results than those did by other optimization algorithms given in the literature. Walraven et al. [12] proposed a new algorithm to minimize traffic flow using RL algorithm. They formulated traffic flow optimization problem as Markov Decision Process and used Q-learning method to reduce traffic congestion. Another application of the RL algorithm has been proposed by Tozer et al. [13] . They developed a new RL algorithm that is able to find optimal solution with several conflicting objectives. The proposed algorithm has been tested on multi-objectives path finding problems with deterministic and stochastic environments.
optimal for all x values. Despite the fact that different meta-heuristic algorithms have been improved especially in last two decades, the contributions of Reinforcement Learning (RL) to this area are still limited comparing to others. Numerous studies such as genetic algorithm based methods [1] [2] , ant colony based algorithms [3] [4] , harmony search approach [5] , modified firefly algorithm [6] and hybrid heuristic methods [7] [8] [9] have been proposed to optimize any given mathematical function. Apart from these applications, there are some attempts for solving engineering problems in different fields using RL based algorithms in the relevant literature. Hsieh and Su [10] developed Q-learning based optimization algorithm for solving economic dispatch problem after they tested their proposed algorithm for optimizing standard mathematical test functions. Their results showed that the proposed algorithm outperformed many existing optimization algorithms. Similarly, Samma et al. [11] tested newly developed RL based Memetic Particle Swarm Optimization algorithm on mathematical functions and real-world benchmark problems. Numerical examples applied indicated that the proposed algorithm is able to produce better results than those did by other optimization algorithms given in the literature. Walraven et al. [12] proposed a new algorithm to minimize traffic flow using RL algorithm. They formulated traffic flow optimization problem as Markov Decision Process and used Q-learning method to reduce traffic congestion. Another application of the RL algorithm has been proposed by Tozer et al. [13] . They developed a new RL algorithm that is able to find optimal solution with several conflicting objectives. The proposed algorithm has been tested on multi-objectives path finding problems with deterministic and stochastic environments.
Although most of the methods described in the literature are able to discover global optimum of any given optimization problem, the performance of newly developed algorithms should be investigated. Therefore, we present a MOdified REinforcement Learning Algorithm (MORELA) approach which differs from RL based approaches by means of generating a sub-environment based on the best solution obtained so far which is saved to prevent the search being trapped at local optimums. And then, all of the function values with corresponding decision variables in MORELA are ranked from best to worst. In this way, the sub-environment is compared with the original environment. If one of the members of the sub-environment produces better functional value, it is added to the original environment and the worst solution is omitted. This makes the searching process more effective because the global optimum is sought around the best solution achieved so far, with the assistance of the sub-environment and the original environment.
RL has been attracted a lot of attention from scientific community for solving different class of problems especially in last decades [14] . In RL, there is a remarkable interaction between agent and environment which contains everything apart from the agent. The agent receives information from the environment through cooperating with each other. Depending on the information obtained, the agent changes the environment by means of implementing an action. This modification is transferred to the agent by means of a signal. The environment generates numerical values called rewards and the agent efforts to maximize them. The agent and environment affect each other at each time  in which the agent gets information about the environment’s state
in which the agent gets information about the environment’s state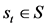 , where
, where 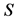 consists of states. To this respect, the agent performs an action
consists of states. To this respect, the agent performs an action , where
, where 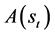 includes actions in state
includes actions in state 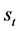 and gains a reward
and gains a reward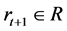 , and it is located in a new state
, and it is located in a new state . Figure 1 represents this cooperation [15] .
. Figure 1 represents this cooperation [15] .
There are three primary types of RL based methods, each with its advantages and disadvantages. The Monte Carlo and Temporal difference learning methods are able to learn only from experience whereas the other one, called Dynamic programming, requires a model of the environment. Therefore, because of not need to have a model, they are superior to Dynamic programming. Indeed, temporal difference learning methods are at the core of RL [16] . On the other hand, Q-learning, one of the temporal difference methods, evaluates Q values, which represent quality of a given state-action pair [17] . It benefits experience to update members of Q table [14] . Q table has elements as  for each state-action pair. The Q-learning determines the Q value, which reflects an action a performed in a state s, and selects the best actions [18] . The Q table is created as shown in Table 1 [19] .
for each state-action pair. The Q-learning determines the Q value, which reflects an action a performed in a state s, and selects the best actions [18] . The Q table is created as shown in Table 1 [19] .
Q learning algorithm includes in a sequence of learning episodes (i.e. iteration). At each learning episode, the agent chooses an action in accordance with information provided from a state s. The agent deserves to receive a reward considering its Q value and observes the next state, . The agent replaces its Q value with that provided according to Equation (1):
. The agent replaces its Q value with that provided according to Equation (1):
 (1)
(1)
![]()
Figure 1. The cooperation between agent and environment.
where ![]() is the updated Q value,
is the updated Q value, ![]() is the Q-value saved in the Q table,
is the Q-value saved in the Q table, ![]() is the reward for state-action pair,
is the reward for state-action pair, ![]() is the learning rate, and
is the learning rate, and ![]() is the discounting parameter [18] .
is the discounting parameter [18] .
This paper proposes a new and robust approach, called MORELA, to optimize any given mathematical function. MORELA approach varies from other RL based approaches through generating a sub-environment. In this way, developed MORELA approach has ability to find global optimum for any given mathematical optimization because it is sought both around the best solution achieved so far with the assistance of the sub-environment and the original environment. The rest of this paper is organized as follows. The definition of fundamental principles of MORELA is provided in Section 2. Section 3, which also contains comparison of MORELA and RL, various contrastive analyses of MORELA such as robustness analysis, comparisons with other related methods, explanation of evolving strategy of MORELA and investigation of the effect of high dimensionality, presents numerical experiments and the last section is conclusions.
2. The MORELA Approach
There are several studies related to RL combined with different heuristic methods for solving different types of optimization problems. Liu and Zeng [20] developed genetic algorithm based method with assistance of reinforcement mutation to tackle the problem of travelling salesman. Integrating RL with different algorithms has been used to address the problem of robot control with unrecognized obstacles [21] . The experimental results revealed that the hybrid approach is superior to RL for planning robot motion whereas RL faced some difficulties. Chen et al. [22] proposed genetic network programming with RL for stock trading. The comparison of the results with those obtained from other methods shows the noticeable performance of their method. Similarly, Wu et al. [23] improved a RL based method considering multi-agent for tackling job scheduling problems. Their results showed that the method is comparable to that of some centralized scheduling algorithms.
From a different viewpoint, Derhami et al. [24] applied RL based algorithms for ranking most relevant web pages to user’s search. The algorithms are tested by using well-known benchmark datasets. Their results showed that the use of RL makes noticeable improvements in ranking of web pages. Khamis and Gomaa [25] used an adaptive RL approach to tackle traffic signal control at junctions by considering multi-objective. Recently, Ozan et al. [26] developed RL based algorithm in determining optimal signal settings for area traffic control. Results revealed that the proposed algorithm outperforms genetic algorithm and hill climbing methods even if there is a heavy demand condition.
Hybridizing RL algorithms with other optimization methods is a powerful technique to tackle different types of optimization problems arising in different fields. Thus, in the context of this paper, we focus on applicability of RL based algorithms to discover global optimum for any mathematical function. The proposed algorithm called MORELA is on the basis of Q-learning, which is a model-free RL approach. In addition, a sub-environment is generated in MORELA so that the environment consists of original and sub-environment differently from other RL based approaches as shown in Equation (2) [26] .
![]() (2)
(2)
where m is the size of the original environment, n is the number of decision variables, and f is fitness value at the tth learning episode. As shown in Equation (2), ![]() value achieved in the previous learning episode is kept in the (m + 1)th row. At the tth learning episode, a sub-environment is generated as given in Equation (3) and located between rows (m + 2) and (2m + 1). Thus, a global optimum is explored around the best solution with assistance of sub-environment with vector of
value achieved in the previous learning episode is kept in the (m + 1)th row. At the tth learning episode, a sub-environment is generated as given in Equation (3) and located between rows (m + 2) and (2m + 1). Thus, a global optimum is explored around the best solution with assistance of sub-environment with vector of ![]() which must be decreased during algorithm process in order to make searching more effectively in a reduced environment. The limits of
which must be decreased during algorithm process in order to make searching more effectively in a reduced environment. The limits of ![]() can be selected by considering upper and lower constraints of a given problem [3] .
can be selected by considering upper and lower constraints of a given problem [3] .
![]() (3)
(3)
After generating the sub-environment, the solution vectors located in both environments are ranked from best to worst according to their fitness values. With assistance of this sorting, the worst solution vector is excluded from environment whereas the solution vector provided a better functional value is included. Thus, MORELA may gain the ability to solve any given optimization problem without prematurely converging. Figure 2 shows the process of MORELA.
In MORELA, each action a in state s is rewarded as shown in Equation (4) [26] .
![]() (4)
(4)
where ![]() is the reward function,
is the reward function, ![]() is the Q value and
is the Q value and ![]() is the best Q value obtained in the tth learning episode. In MORELA, the reward value is determined for each member of the solution vector by considering its Q value and the best Q value provided so far. The reward values come to close to the value “0” at the end of the solution process because of the structure of the reward function. In fact, a solution receives less reward when it is located closer to global optimum than the others. On the other hand, the probability of global optimum finding for further located solutions may be increased by means of providing them bigger rewards. Thus, the reward function developed may be referred to as penalty contrary to reward.
is the best Q value obtained in the tth learning episode. In MORELA, the reward value is determined for each member of the solution vector by considering its Q value and the best Q value provided so far. The reward values come to close to the value “0” at the end of the solution process because of the structure of the reward function. In fact, a solution receives less reward when it is located closer to global optimum than the others. On the other hand, the probability of global optimum finding for further located solutions may be increased by means of providing them bigger rewards. Thus, the reward function developed may be referred to as penalty contrary to reward.
3. Numerical Experiments
An application of MORELA was carried out by solving several mathematical functions taken from the literature. However, before solving these functions, it may be essential to demonstrate the effectiveness of MORELA over RL. For this purpose, a performance comparison was conducted by solving a mathematical function. MORELA was encoded in the MATLAB for all test functions, using a computer with Intel Core i7 2.70 GHz and 8 GB of RAM. The related solution parameters for MORELA were set as follows: the environment size is taken as 20, the discounting parameter ![]() and the learning rate
and the learning rate ![]() were taken as 0.2 and 0.8, respectively. The search space parameter
were taken as 0.2 and 0.8, respectively. The search space parameter ![]() was chosen according to the search domain for all test functions. The solution process was terminated when a pre-determined stopping criterion was met. The stopping criterion was properly selected for each function, and it theoretically guarantees that global optimum will be found eventually.
was chosen according to the search domain for all test functions. The solution process was terminated when a pre-determined stopping criterion was met. The stopping criterion was properly selected for each function, and it theoretically guarantees that global optimum will be found eventually.
3.1. Comparison of MORELA and RL
The test function used to compare MORELA and RL is given in Equation (5). It has a global optimum solution of ![]() when
when![]() . A graph of the objective function is given in Figure 3. The convergence behaviors of MORELA and RL are illustrated in Figure 4.
. A graph of the objective function is given in Figure 3. The convergence behaviors of MORELA and RL are illustrated in Figure 4.
![]() (5)
(5)
As seen in Figure 4, same initial solutions were used for both algorithms to compare them realistically. Simulation results reveal that MORELA requires many fewer learning episodes than RL although both algorithms are capable of finding globally optimal solution for this function. MORELA needs only 1176 learning episodes to find optimal solution whereas RL requires 7337.
![]()
Figure 3. Objective function within the range (−10, 10).
![]()
Figure 4. Performance comparisons of MORELA and RL.
3.2. Robustness Analysis
A robustness analysis for MORELA was carried out by using succeed ratio (SR) given in Equation (6).
![]() (6)
(6)
where Ns is the number of successful runs which indicates that the algorithm produces the best solution at the required accuracy and NT is the total number of runs which is set to 50 to make a fair comparison. For this experiment, a run is accepted as successful when its objective function value is around 3.5% of global optimum. The robustness analysis for MORELA, PSACO [7] and other methods [27] are given in Table 2. As shown, MORELA is able to find global optimum with very high success in comparison with other algorithms, except PSACO. Although PSACO produces higher success ratios than MORELA for functions F12 and F13, for given total numbers of runs, MORELA and PSACO yield same results for functions F2, F7, F9 and F16. CPSO, PSO and GA in particular yield worse results than MORELA and PSACO.
3.3. Further Comparisons of MORELA with Other Methods
To gauge the performance of MORELA against the performance of some other methods described in the literature, sixteen well-known benchmark problems were used which are given in Appendix A. Functions 6, 7, 9, 13 and 16 are taken from Shelokar et al. [7] . Functions 8 and 14 are adopted from Sun and Dong [28] and Chen et al. [29] , respectively. The rest of the functions are from Baskan et al. [3] . Table 3 lists algorithms compared with MORELA.
To assess the ability of MORELA, its performance was compared with 12 algorithms listed in Table 3. For this purpose, sixteen test functions were used based on 100 runs. The results are shown in Table 4 in terms of the best function value, the number of learning episodes, the best solution time, the success ratio, the average number of learning episodes and the average error. The best function value is the value obtained for all runs at the required accuracy that indicates that the algorithm reached to the global optimum. The required accuracy is determined as the absolute difference between the best function value and the theoretical global optimum. For this experiment, a value of “0” was chosen as required accuracy for all test functions. The number of learning episodes and the best solution time are the number of runs and the time required to obtain the best function value, respectively. The average number of learning episodes is de-
![]()
Table 2. Results of robustness analysis.
![]()
Table 3. The algorithms compared with MORELA.
![]()
![]()
Table 4. The results of MORELA and compared algorithms.
NA: Not available; aThe average number of function evaluations of four runs and running time in units of standard time. bThe theoretical minimum value was considered to be four digits. cThe theoretical minimum value was considered to be two digits. dMean results of more than 30 independent trials.
termined based on the number of successful runs in which algorithm generates the best solution for the required accuracy. Average error is defined as the average of the difference between best function value and theoretical global optimum.
The findings indicate that the MORELA showed remarkable performance for all of the test functions except F3, for which theoretical global optimum could not be found with the required accuracy, namely, 0. Although MORELA was not able to solve this function, it produces better functional value than those provided by other compared algorithms, as shown in Table 4. MORELA also produces less average error for all test functions than the other methods considered. At the same time, most of these errors are equal to 0. This means that MORELA was able to find the global optimum for each run. Therefore, MORELA may be considered to be a robust algorithm for finding global optimum for any given mathematical function. As Table 4 shows, MORELA requires a greater number of learning episodes than the other algorithms for many of the test functions, due to accuracy required of it. Although the required number of learning episodes was found to be higher than the other algorithms, it can be ignored because of the required accuracy chosen (a value of 0) for all test functions considered in this comparison. The best solution times for the functions achieved by the algorithms considered are also given in Table 4. In the meantime, investigation of the effect of environment size and corresponding algorithm parameters is the beyond the scope of this study.
3.4. Explanation of Evolving Strategy Provided by Sub-Environment
In addition, we have used Bohachevsky function (F4) in order to better explain how the evolving population is diversified by the sub-environment in MORELA. The function of F4 has a global optimum solution of ![]() when
when ![]() for the case of 2 variables and the required accuracy was chosen to be 1e−15 units for this experiment. As it can be realized from Figure 5(a) and Figure 5(b), the sub-environment is firstly generated at 2nd learning episode using Equation (3), depending on the best solution found in the previous learning episode and
for the case of 2 variables and the required accuracy was chosen to be 1e−15 units for this experiment. As it can be realized from Figure 5(a) and Figure 5(b), the sub-environment is firstly generated at 2nd learning episode using Equation (3), depending on the best solution found in the previous learning episode and ![]() value.
value.
When the main difference between Figure 5(a) and Figure 5(b) is observed, it can be clearly seen that the solution points are stably distributed in the original environment whereas the points in the sub-environment explore global optimum near the boundaries of the solution space given as ![]() for this function. Although the solution points located in the original environment have a tendency to reach global optimum at the 10th learning episode as shown in Figure 5(c) and Figure 5(d), the others located in the sub-environment still continue to search global optimum near the boundaries of the solution space. This property provides to diversify the population of MORELA at each learning episode, and thus the probability of being trapped in local optimum is decreased. At 25th learning episode, the solution points in the original environment are almost close to global optimum, but the other points in the sub-environment are still dispersed in the solution space as can be seen in Figure 5(e) and Figure 5(f). Similarly, this tendency continues until MORELA reached to about 200th learning episode. After 250th learning episode, the solution points in the original environment are too close to global optimum whereas the others in the sub-environment still continues to explore new solution points around global optimum although they have a tendency to reach global optimum. Finally, at
for this function. Although the solution points located in the original environment have a tendency to reach global optimum at the 10th learning episode as shown in Figure 5(c) and Figure 5(d), the others located in the sub-environment still continue to search global optimum near the boundaries of the solution space. This property provides to diversify the population of MORELA at each learning episode, and thus the probability of being trapped in local optimum is decreased. At 25th learning episode, the solution points in the original environment are almost close to global optimum, but the other points in the sub-environment are still dispersed in the solution space as can be seen in Figure 5(e) and Figure 5(f). Similarly, this tendency continues until MORELA reached to about 200th learning episode. After 250th learning episode, the solution points in the original environment are too close to global optimum whereas the others in the sub-environment still continues to explore new solution points around global optimum although they have a tendency to reach global optimum. Finally, at
![]()
![]()
Figure 5. An illustration of diversify mechanism of MORELA.
1000th learning episode, all solution points populated in the original and sub-environment reached to global optimum as seen in Figure 5(k) and Figure 5(l).
3.5. Effect of High Dimensions
The Ackley function given in Equation (7) was chosen to explore the effect of high dimensions on the search capability of MORELA. The global minimum of this function is given as ![]() at
at![]() . The algorithm was repeated 10 times to decrease the effect of randomness. The average number of learning episodes and average objective function values were recorded with different dimensions. For this experiment, the required accuracy was chosen to be 1e−10 units.
. The algorithm was repeated 10 times to decrease the effect of randomness. The average number of learning episodes and average objective function values were recorded with different dimensions. For this experiment, the required accuracy was chosen to be 1e−10 units.
![]() (7)
(7)
・ ![]()
・ ![]()
Figure 6 represents the variation of the average objective function value according to different dimensions.
As Figure 6 shows, the MORELA shows acceptable performance even for high dimensions of the Ackley function. Average objective function values of 9.74e−11 and 9.89e−11 were obtained when the dimensions were equal to 10 and 10,000, respectively. These values are very close to each other, considering differences in dimensions. Results show that MORELA may be considered as an efficient way for finding global optimum based on required accuracy of a given mathematical function even if dimension of the problem became increased. Figure 7 illustrates the variation in the average number of learning episodes as a function of dimension for the Ackley function.
Although the average number of learning episodes increased notably with increasing dimension up to 1000, the average number of learning episodes increased very little within the dimension range from 1000 to 10,000. This experiment clearly demonstrates that the number of learning episodes required by MORELA is not apparently affected by high dimensionality.
4. Conclusions
A powerful and robust algorithm called MORELA is proposed to find global op-
![]()
Figure 6. Average objective function values with different dimensions.
![]()
Figure 7. Average number of learning episodes with different dimensions.
timum for any given mathematical function. MORELA differs from RL based approaches by means of generating a sub-environment. Thus, this approach makes it possible to find global optimum, because it is sought both around the best solution achieved so far with the assistance of the sub-environment and the original environment.
The performance of MORELA was examined in several experiments, namely, a comparison of MORELA and RL, a robustness analysis, comparisons with other methods, explanation of evolving strategy of MORELA, and an investigation of the effect of high dimensionality. The comparison of MORELA and RL showed that MORELA requires many fewer learning episodes than RL to find global optimum for a given function. The robustness analysis revealed that MORELA is able to find global optimum with high success. MORELA was also tested on sixteen different test functions that are difficult to optimize, and its performance was compared with that of other available methods. MORELA has found global optimum for all of the test functions except F3, based on the required accuracy. Besides, the last experiment clearly shows that MORELA is not significantly affected by high dimensionality.
Finally, all numerical experiments indicate that MORELA performed well in finding global optimum of mathematical functions considered, compared to other methods. Based on the results of this study, it is expected that in future research, optimization methods based on RL will be found to possess great potential for solving various optimization problems.
Appendix A
F1:
Rosenbrock (2 variables)
![]()
・ global minimum: ![]()
F2:
(2 variables)
![]()
・ ![]()
・ global minimum: ![]()
F3:
(2 variables)
![]()
・ global minimum: ![]()
F4:
Bohachevsky (2 variables)
![]()
・ ![]()
・ global minimum: ![]()
F5:
De Jong (3 variables)
![]()
・ ![]()
・ global minimum: ![]()
F6:
Easom (2 variables)
![]()
・ ![]()
・ global minimum: ![]()
F7:
Goldstein-Price (2 variables)
![]()
・ ![]()
・ global minimum: ![]()
F8:
Drop wave (2 variables)
![]()
・ ![]()
・ global minimum: ![]()
F9:
Shubert (2 variables)
![]()
・ ![]()
・ 18 global minima ![]()
F10:
Schwefel (2 variables)
![]()
・ ![]()
・ global minimum: ![]()
F11:
Zakharov (2 variables)
![]()
・ ![]()
・ global minimum: ![]()
F12:
Hartman (3 variables)
![]()
・ ![]()
・ global minimum: ![]()
F13:
Hartman (6 variables)
![]()
・ ![]()
・ global minimum: ![]()
F14:
Rastrigin (2 variables)
![]()
・ ![]()
・ global minimum: ![]()
F15:
Griewank (8 variables)
![]()
・ ![]()
・ global minimum: ![]()
F16:
Branin (2 variables)
![]()
・ ![]()
・ three global minimum: ![]()