Performance Evaluation of OFDM Coding System Using Concatenated BCH and LDPC Codes ()
1. Introduction
Digital video broadcasting (DVB) [1] systems have stipulated the accomplishment of superior information rates, delivering efficient data transmission over error prone environment. Such systems utilize Orthogonal Frequency Division Multiplexing (OFDM) along with FEC (forward error correction) scheme that culminates in fast transmission incorporating M-ary QAM [2] modulation techniques. The high spectral efficiency of M-ary QAM and superior information rates is achieved by OFDM results in an efficient communication system.
By and large, the advantage of a multi-carrier system is that it can be largely unaffected by inter-symbol interference (ISI) by using pulse shaping filters. However, the OFDM system is extremely prone to frequency offset brought about by multipath delay spread channels. These frequency offsets impact the orthogonality of OFDM subcarriers, and it will likewise experience the inter-carrier interference (ICI). High data rates, along with spectral efficiency are achieved using OFDM which is an efficient technique to compensate rate loss caused by concatenation of codes [2]. OFDM strategies have served as basic building blocks for many of the current modulation schemes incorporated in Digital TV (DVB-T/T2, DVB-H, DMB-T/H, DVB-C2), Wireless LAN IEEE 802.11 a, IEEE 802.11 g, IEEE 802.11n, IEEE 802.11 ac, and IEEE 802.11 ad, Worldwide Interoperability for Microwave Access (WiMAX), Light Fidelity (Li-Fi), ADSL (Advanced Digital Subscriber Line), LTE Advanced 4G and 5G mobile phone standards, etc. [3].
The advent of Low Density Parity Check (LDPC) code was introduced by Gallager in 1963 [4]. Mostly ignored, Tanner’s work in 1981 brought to light the robust LDPC technique, but during that time computers were not powerful enough and were forgotten for decades. In 1995 it was re-found by MacKay and Neal sparking a flurry of further research [5]. Gallager’s simulation results demonstrated that these codes were processed on following the likelihood ratio or distribution of the extrinsic information exchanged during the message passing decoding standards, and it can approach Shannon limit while expanding code length. Besides, Gallager proposed a pragmatic iterative calculation that utilized extrinsic information traded between bit nodes and check nodes for decoding these codes. These codes can be decoded using various techniques ranging from high complexity to low complexity conversely providing satisfactory to exceptional error performance. Briefly, LDPC codes are linear block codes whose parity check matrix is exceptionally sparse. BCH code is a cyclic code that is built from Galois field. It was proposed by Hocquenghem in 1959, though done autonomously it was additionally found by Bose and Ray-Chaudhuri in 1960. In coding theory, concatenated codes form a class of error-correcting codes that are derived by combining an inner code and an outer code. They were conceived in 1966 by Dave Forney as a solution to the problem of finding a code that has both exponentially decreasing error probability with increasing block length and polynomial-time decoding complexity.
This paper implements Forward Error Correction (FEC) scheme using concatenation of BCH and LDPC codes, with BCH as the external encoder and LDPC as internal encoder for OFDM system with M-ARY QAM over AWGN channel [6] [7]. Also the variation in performance of the coding system with varied codeword lengths and check bit lengths is established.
This paper henceforth is organised in the following sections. Section 2 describes the proposed model as shown in Figure 1 along with the basic overview of the coding scheme and the algorithms incorporated. Section 3 illustrates simulation results juxtaposed with graphical representations to establish the intent of the topic and provide an analysis of the performance of the above incorporated coding system. Section 4 provides a conclusion to indicate the system’s modern day relevance in terms of its performance parameters.
2. System Description
We have put forth an efficient scheme which involves the concatenation of
![]()
Figure 1. The concatenated coded OFDM based communication system.
LDPC codes with BCH codes, which is based on OFDM modulation over AWGN channel along with a random interleaving and de-interleaving scheme. In our proposed model we use a BCH encoder as the outer encoder and LDPC encoder as the inner encoder. The block diagram of the proposed system is as shown in Figure 1. We intend to compare the performance of the system with M-ary QAM within OFDM. The Decoding algorithm for BCH used is Berlekamp-Massey algorithm and Sum product algorithm for the decoding of LDPC codes.
A. BCH encoder
These codes are a summed up type of Hamming codes that permits various error correcting capabilities. They shape a class of effective arbitrary error redressing cyclic codes which gives a determination of bigger block lengths, code rates and error revising capacity [6].
BCH codes are characterized by the following parameters:
For any positive integer value of m where m ≥ 3 and t where t is the error correcting capability variable indicated by t < 2m − 1. A BCH code can be designed with the following parameters.
where,
Length of the code: NBCH = 2m − 1 (1)
Total number of parity checks bits:
NBCH-KBCH ≤ mt
Minimum distance: dmin≥ 2t + 1
This code is capable of correcting t or fewer errors in a block of codes of size n, this is called as t error correcting BCH codes. There is a need to determine the generator polynomial to define encoding technique. The generator polynomial is defined in terms of roots from the Galois field GF (2m). The generator polynomial of the t-error rectifying BCH code of length 2m − 1 is the most reduced degree polynomial over GF(2) that has α, α2, α3, α4, α5, α6 …………., α2t as its roots. Let ϕ(x) be the minimal polynomial of αi. Then g(x) must be Least Common Multiple (LCM) of the product of ϕ1(x), ϕ2(x),….. ϕ2t(x).
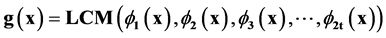 (2)
(2)
Since all the even powered values of α in the sequence α, α2, α3, α4, α5, α6 ………….,α2t has the same minimal polynomial as the preceding odd power of α in the sequence. Ignoring the minimal polynomials of the even power values of α results in generator polynomial g(x) of the t-error correcting BCH code as
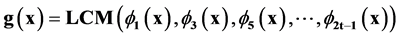 (3)
(3)
For example generator polynomial for a double error correcting code is:
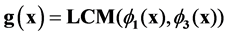 (4)
(4)
Gives a BCH codes which is a (15, 7) cyclic codes
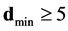 (5)
(5)
Therefore the final Codeword is obtained by:
Codeword = (Message bits)*(gen bits)
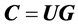 (6)
(6)
B. BCH decoder
The very well-known algorithm used for binary BCH codes is Berlekamp Iterative Decoding Algorithm and hence hereafter the algorithm implemented in the decoding technique [6].
Ø By keeping the received polynomial r(x) syndromes S = (S1, S2, …..S2t) are calculated.
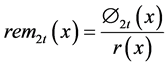 (7)
(7)
where t = error correcting Capability of code.
After finding the remainder polynomial syndromes are calculated by replacing X instead of
Therefore
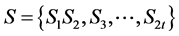 (8)
(8)
After finding the syndromes, using the iterative procedure error Location polynomials
are computed from these syndrome components S1, S2, …….S2t
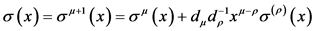 (9)
(9)
where
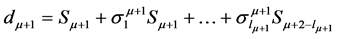
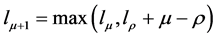
where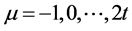 ,
, 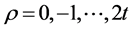 (Table 1).
(Table 1).
Ø Then determine the error sets e(x).
The error sets are found by finding the roots of  .
.
Ø Adding e(x) to the received polynomial r(x) we obtain the codeword
C. LDPC codes
LDPC codes are a class of linear block codes. In an H matrix of size m by n is low thickness in light of the way that the amount of 1s in each row wr is << m and the amount of 1s in each column wc is << n. A LDPC is regular if wc is predictable for every column and wr = wc (n = m) is also reliable for each column. Else it is irregular [5]. In LDPC encoding, the codeword (C0, C1, C2, C3... Cn) involves the message bits (M0, M1, M2… MK) besides, some fairness check bits and
![]()
Table 1. Initial decoding table to find error Location polynomial.
the scientific articulations are gotten from H network to create equity check bits. Their key great position is that they give an execution which is near as far as possible for a mixed bag of channels and straight time complex computations for disentangling. Other than they are suited for use that makes overpowering use of parallelism.
D. Matrix representation and Tanner Graph of LDPC codes
There are numerous ways codes can be represented in graph representation using coding theory. Tanner graph is the best way of representing LDPC codes in graphical format as shown in Figure 2. The tanner graph simplifies and gives good information about parity check matrix and also simplifies the explanation of decoding algorithm. As this graph consists of two opposite nodes tanner graphs can also be called as bipartite graphs.
For example:
Let us consider a parity check matrix H and the tanner graph for it as shown in the below diagram
![]() Parity check Matrix HE. LDPC encodingParity Check Matrix H: (n, wc, wr): Parse MatrixwhereØ n―number of rowsØ wc―number of ones in columnØ wr―number of ones in rowØ Systematic Generator matrix G is obtained by doing row operations on H matrix.where
Parity check Matrix HE. LDPC encodingParity Check Matrix H: (n, wc, wr): Parse MatrixwhereØ n―number of rowsØ wc―number of ones in columnØ wr―number of ones in rowØ Systematic Generator matrix G is obtained by doing row operations on H matrix.where (10)where K is the size of message bits. (P is a dense matrix) and
(10)where K is the size of message bits. (P is a dense matrix) and![]()
Figure 2. Tanner graph of H.
![]() (11)
(11)
Ø If we have message m of k bits then the codeword is obtained by
![]() (12)
(12)
Ø Complexity of encoding is a function of n3 where n is the number of XOR operations done between rows to generate a generator matrix
F. LDPC decoding
There are several novel methods used in decoding LDPC codes. The most common one are Bit Flipping Algorithm (BFA) and Sum Product Algorithm (SPA). The following illustration gives knowledge on Bit Flipping Algorithm which is normally based on hard decision decoding and Sum Product algorithm based on soft decision decoding.
Sum product algorithm
Soft decision decoding of LDPC codes, which depends on the idea of belief propagation yields in a superior decoding performance and therefore belief propagation is the preferred decoding algorithm for LDPC codes. The soft decision decoder works with the same rule as the hard-choice decoder, aside from that the messages are the conditional probability that the received bit is a 1 or a 0 based on the given received vectory. Let Pi = Pr(ci = 1|yi) be the conditional probability that ci is a 1 given the estimation of y and let Pr(ci = 1|yi) = 1-Pi. qij is a message sent by the variable node ci to the check node vj. Each message contains dependably the pair qij(0) and qij (1) which remains for the amount of belief that yi is a “0” or a “1”.
rji is a message sent by check node to variable node. There is rji(0) and rji(1) that indicates the amount of belief in that yi is a “0” or a “1” [8].
Step 1: Compute the initial value of Log Likelihood Ratio (LLR) transmitted from the variable node
to check node
for all I where ![]()
![]() (13)
(13)
where ![]() denotes the channel noise variance and
denotes the channel noise variance and ![]() denotes the probability value for a given input
denotes the probability value for a given input
Step 2: Find ![]() transmitted from the check node
transmitted from the check node ![]() to variable node
to variable node ![]() for all i;
for all i; ![]()
![]() (14)
(14)
where
![]()
![]()
![]()
Step 3: After computing ![]() it is necessary to find the modification of
it is necessary to find the modification of ![]() which is used to find the data transmitted from the variable node
to check node
which is used to find the data transmitted from the variable node
to check node ![]() for all i where
for all i where![]() .
.
![]() (15)
(15)
Step 4: The soft output obtained can be represented as:
![]() (16)
(16)
Step 5: Once we obtain the soft output then hard decision is made to figure out the output by
![]() (17)
(17)
It is found that the soft decision decoding method for LDPC decoder gives much better result compared to hard decision decoding. Therefore soft decision decoding method is chosen for decoding using LDPC in the proposed research work.
3. Simulation Results
The proposed scheme’s performance was investigated using MATLAB which involves the transmission of an image through a Forward Error Correction coding system whose integrity depends on OFDM with M-ary QAM transmitted through an AWGN channel. The scheme proposed here implements 4K OFDM with 128 sub-frames and the simulated results for an un-coded system are given in Figure 3, where we observe Bit error rates ranging from 10−0.48 to 10−0.68 for decreasing order of M-ary QAM. The simulated results as shown in the Figure 4 represent the received image, where adistorted image is obtained even after reaching higher SNR values. Figure 5 is a graph of BER vs SNR for coded system without an Interleaver for various values of M(4, 8, 16, 32, 64, 128, 256). Here BER values drop to almost 10−3, hence significant error correcting capabilities which result in an undistorted image as shown in Figure 6. The system establishes high coding gain as seen from the graphs shown in Figure 3 and Figure 5.
We also noticed that by implementation of BCH as the outer decoder reduced error floor at comparatively higher SNRs. In this coding system the LDPC decoder in the concatenated scheme has increased the error correcting capability.
![]()
Figure 3. Uncoded scheme for M-ary QAM using OFDM.
![]()
Figure 4. Image received for an uncoded scheme.
![]()
Figure 5. Concatenated coding scheme for M-ary QAM using OFDM without Interleaver.
![]()
Figure 6. Image received for a coded scheme.
Inclusion of the Interleaver in this proposed scheme reduces burst errors and thus allows higher error correcting capability of the concatenated coding system. Concatenated codes inevitably lead to rate loss and thus decreasing its spectral efficiency. The OFDM system implemented in our proposed scheme compensates for this rate loss because of its high spectral efficiency. The BER increases gradually as SNR values increase and this scheme is suitable for higher order M-ary QAM (64QAM and 256 QAM).The considered LDPC codes parity check matrix corresponds to an irregular LDPC code with a code rate = 1/2 (32,400/ 647800) where the block length of the code is 64,800.
Our further research includes performance evaluation of 256-QAM using an Interleaver as shown in Figure 7. We have found that the BER has significantly been enhanced resulting in 10−6. On comparing a coded system with Interleaver and one without an Interleaver, a difference of around 15 dB was seen at a BER of 10−3.
Figure 8 shows simulation results using different values of code word length denoted by n = 255, 63, 15 and message length denoted by k = 247, 57, 5 with error correcting capability denoted by t = 1, 1, 3 respectively. The following per-
![]()
Figure 7. Concatenated coding scheme for 256-QAM using OFDM with Interleaver.
![]()
Figure 8. Concatenated coding scheme for different BCH code rates using OFDM and 256 QAM.
formance of different n, k values as shown in the Figure 8 indicate that larger codeword length exhibit higher SNR values. Both the single error correcting capability codes exhibit a bit error of around 10−6 at 28 dB SNR. However the triple error correcting code exhibits an bit error rate of near 10−5 at low SNR of 24 dB. A balance must be struck between codeword length n, error correcting capability t and SNR to meet various requirements.
4. Conclusions
This paper establishes that a system involving the concatenation of LDPC and BCH codes provides good error correcting capabilities at moderately low SNR values. In this paper the new coding scheme is investigated and it is seen that the concatenation of codes diminishes the effect of error floor, simultaneously enhancing the coding system’s error correcting capability. The concatenation of codes inevitably leads to rate loss and decrease spectral efficiency, OFDM’s inclusion compensates for the prior problem thus making it one of the most effective systems for present day and future solutions in digital video broadcasting applications.
Further we are planning to enhance the performance of the above concatenated coding scheme by using polar codes replacing LDPC codes. Polar codes are extended version of non-binary BCH codes which uses successive cancellation algorithm for successful decoding. These codes can outperform LDPC and Turbo codes.
Acknowledgements
The authors thank DR A.G. Nataraj, Principal, Bangalore Institute of Technology, Bengaluru, India for his support and encouragement and Dr. Sree Ranga Raju M N, Professor, Department of Electronics and Communication Engineering, Bangalore Institute of Technology, Bengaluru, India for his constant support and guidance throughout the course of preparing this paper.