1. Introduction
Electrical Impedance Tomography (EIT) is a radiation-free imaging method. It attempts to reveal the conductivity distribution changes inside the human body of two time instants through electrical data obtained via the electrodes attached to the boundary. In lung EIT, commonly 16 electrodes are placed equidistantly on the boundary of a horizontal chest plane.
We denote the conductivity of the domain changes between two time steps by 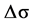 and the measured voltage changes on the electrodes by a vector
and the measured voltage changes on the electrodes by a vector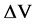 . Under the FEM framework with
. Under the FEM framework with 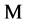 elements, the conductivity change
elements, the conductivity change  is represented by a
is represented by a 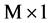 vector. Approximately, there exists the following relation:
vector. Approximately, there exists the following relation:
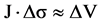 (1)
(1)
where 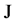 denotes the Jacobian matrix calculated at the constant conductivity 1:
denotes the Jacobian matrix calculated at the constant conductivity 1:
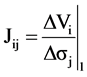 (2)
(2)
Jacobian matrix is commonly calculated by studying the first order perturbation of conductivity on each element [1]. Briefly, under FEM framework, the potential distribution can be solved by forward model. The perturbations on each element can be determined by the simulated potential information [1].
However, such linearized forward and inverse model contains modeling error. EIT reconstruction is a non-linear inverse problem. There are many modelling error affects the imaging quality of EIT. For example, the deformations of the boundary shape the inhomogeneous background conductivity as well as the shift of contact impedance on the electrodes. In this study we focus only on the modelling error caused by linearization. To this end, we simplify the simulation models by specifying the domain shape to be unit disk and the known background conductivity.
2. Methods
2.1. EIT Current Injection and Measurement
On the currently available EIT devices, all electrical boundary conditions are collected through the electrode-band located around a plane of the human body. The electrical current injection and voltage measurement are always performed with a period scheme. The most commonly employed of the current injection and voltage measurement pattern is called adjacent pattern. At each time step, alternative currents with fixed amplitude are sequentially injected through two neighboring electrodes (Figure 1). For each current injection, the induced voltages are measured through adjacent electrodes with a fixed order. By fixing the injection and measurement pattern, the voltage measurement can be saved as a vector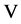 . According to Ohm’s law this voltage measurement is only depending on the conductivity distribution within the domain. In simulations, the voltage measurements are calculated through forward model. We will outline this forward model in Section 2.2.
. According to Ohm’s law this voltage measurement is only depending on the conductivity distribution within the domain. In simulations, the voltage measurements are calculated through forward model. We will outline this forward model in Section 2.2.
2.2. Voltage Measurement Calculated from Maxwell’s Equation
In this subsection we outline the forward model calculation based on Maxwell’s equation. In order to simplify the formulations, we employ the shunt model boundary value problem. This model neglects the effect of contact impedance. In the absence of interior current sources, there is Ohm’s law:
![]()
Figure 1. Adjacent current injection and voltage measurement pattern. In this pattern, 32 electrodes are attached around the boundary of the domain. Alternative current with 5mA are injected from the neighboring electrodes. The induced voltages are measured through the adjacent electrodes.
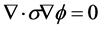 (3)
(3)
where 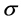 is the conductivity distribution in the domain and
is the conductivity distribution in the domain and 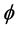 is the voltage distribution in the domain. Note that, with a given conductivity distribution
is the voltage distribution in the domain. Note that, with a given conductivity distribution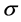 , the left hand of Equation (1) presents a linear mapping of the voltage distribution
, the left hand of Equation (1) presents a linear mapping of the voltage distribution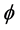 . In principle, the voltage distribution within as well as on the boundary of the domain can be obtained by solving this linear equation. Commonly, this equation is solved with the help of FEM method. An example of the voltage distribution for a conductivity distribution (Figure 2(a)) has been demonstrated (Figure 2(b)). This voltage distribution is calculated by using EIDORS toolbox [2]. Hence the voltage measurement differences along the boundary between two time steps can also be exactly calculated.
. In principle, the voltage distribution within as well as on the boundary of the domain can be obtained by solving this linear equation. Commonly, this equation is solved with the help of FEM method. An example of the voltage distribution for a conductivity distribution (Figure 2(a)) has been demonstrated (Figure 2(b)). This voltage distribution is calculated by using EIDORS toolbox [2]. Hence the voltage measurement differences along the boundary between two time steps can also be exactly calculated.
2.3. Voltage Calculated from the Linearized Model
With a given conductivity distribution, the Jacobian matrix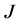 , also called the sensitivity matrix, can be calculated. Intuitively, a row of
, also called the sensitivity matrix, can be calculated. Intuitively, a row of 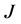 represents the response of the voltage changes with respect to small impedance changes of each FEM element. In real applications, the actual conductivity distribution is unknown. In EIT society, the Jacobian matrix is commonly calculate with respect to the homogenous conductivity distribution:
represents the response of the voltage changes with respect to small impedance changes of each FEM element. In real applications, the actual conductivity distribution is unknown. In EIT society, the Jacobian matrix is commonly calculate with respect to the homogenous conductivity distribution: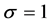 . We adopt this convention in this study. According to the linearized model, expressed as Equation (1), the voltage difference between two time points can be approximately calculated by simply multiply the Jacobian matrix
. We adopt this convention in this study. According to the linearized model, expressed as Equation (1), the voltage difference between two time points can be approximately calculated by simply multiply the Jacobian matrix 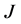 and the conductivity changes. On the other hand, the exact voltage differences between two time steps can be calculated according to Section 2.2. Under the specified adjacent simulation settings, the discrepancy between these two voltage differences is because of the modeling error induced by linearization. Explicitly, the following discrepancy is identified as the modeling error induced by linearization:
and the conductivity changes. On the other hand, the exact voltage differences between two time steps can be calculated according to Section 2.2. Under the specified adjacent simulation settings, the discrepancy between these two voltage differences is because of the modeling error induced by linearization. Explicitly, the following discrepancy is identified as the modeling error induced by linearization:
![]() (a) (b)
(a) (b)
Figure 2. Conductivity distribution and the voltage distribution changes. For a given conductivity distribution (shown in left image), the voltage distribution changes with respect to a current injection can be calculated through Maxwell’s equation. This voltage distribution changes is exact. The simulated voltage measurment changes arround the boundary can be derived from this voltage distribution changes.
Linearization error: = ![]() (4)
(4)
2.4. Simulation Phantom
The discrepancy between the voltage differences calculated from Maxwell’s equation and the linearized model will be studied through simulation. A 2D disk FEM model was constructed with the help of MATLAB toolbox EIDORS. This model has 1215 triangular elements. Around the boundary of the disk phantom, 16 electrodes are attached equidistantly. The contact impedance between each electrode and the disk domain is fixed to be 0.01 Ω∙m. The simulated current with the amplitude of 10 mA was injected through these electrodes with the adjacent pattern. Different conductivity contrasts are embedded into this disk phantom. In this first study, we increase the constant conductivity of the contrast region from 1.01 Sm−1 to 2 Sm−1. These simulated phantoms reflex the different aspects of the contrasts. Such as different location, size as well as asymmetry.
3. Results and Discussion
In this section, we present the first simulation results. We employ the 2D FEM model with disk shape for simulation as displayed in section 2.4. The linearization modeling errors, pronounced by the voltage discrepancy descript in the last section will be studied. In below the modeling errors induced by linearization are studied with respect real to the voltage changes. The relation between modeling errors and voltage differences will be investigated according to each of the four given phantoms. For the phantom A with contrast conductivity![]() , the real voltage differences were demonstrated in the left plot of Figure 4. The corresponding modeling error, defined by Equation (4), is plotted in the same figure. For three different conductivities:
, the real voltage differences were demonstrated in the left plot of Figure 4. The corresponding modeling error, defined by Equation (4), is plotted in the same figure. For three different conductivities:![]() ,
,![]() and
and![]() , the absolute value of the modeling error with
, the absolute value of the modeling error with
![]()
Figure 3. Simulation phantoms. Four different phantoms are used for simulation. Each of them has a disk shape with diameter equals 1m.. The background conductivity of these phantoms is 1 Sm−1. For each given value![]() , a contrast with conducitivity σ will be embedded into the background phantom. Conductivity contrasts with different shapes were embedded into the phantoms. Simulated voltages will be calculatd from these phantom. The voltage difference between the simulated voltages calculated before and after contrasts embedding will be considered as the real voltage difference.
, a contrast with conducitivity σ will be embedded into the background phantom. Conductivity contrasts with different shapes were embedded into the phantoms. Simulated voltages will be calculatd from these phantom. The voltage difference between the simulated voltages calculated before and after contrasts embedding will be considered as the real voltage difference.
respect to the voltage differences are further studied by linear regression. This regression result has been displayed in the right plot of Figure 4, where each dot represents a pair of error and voltage difference data. According to the similar scheme, based on phantom B, C and D, the same plots of the linearization error and the real voltage differences are demonstrated in Figures 5-7.
It can be observed from left plot of Figure 4 that there is a correlation between the linearization error and the real voltage difference. Such correlation can be identified by the linear regression plotted in the right figure of Figure 4. The regression plot indicated a linear relation between the absolute value of the modeling error and the voltage difference. Moreover, with a larger conductivity changes, the slope of the regression is larger. This effect indicates a larger modeling error when the conductivity changes increasing. The same correspondence can be observed in Figure 5 and Figure 6. However, when the asymmetry appears, such as in the case of phantom D, the linear correspondence between modeling error and the voltage differences is not evident.
![]()
Figure 5. Voltage differences and the modeling error induced by linearization. This is the same plot as Figure 4 with respect to the phantom B.
![]()
Figure 6. Voltage differences and the modeling error induced by linearization. This is the same plot as Figure 4 with respect to the phantom C.
4. Conclusion
In this study, the modeling errors induced by linearization are investigated according to simulation. The first simulation results indicated that such modeling
![]()
Figure 7. Voltage differences and the modeling error induced by linearization. This is the same plot as Figure 4 with respect to the phantom D.
errors may have linear correspondence with the voltage differences. An exceptional case appears when the contrast’s shape has large asymmetry. For this situation, the linear correspondence is not obvious.
Acknowledgements
This work is partially supported by the Federal Ministry of Education and Research (BMBF) under grant no. 03FH038I3 (MOSES).