Optimal Replacement Time of Electrical Components Based on Constant-Interval Replacement Model: Equipment Inspection Method and Weibull Analysis ()
1. Introduction
Reliability is an important issue for electric power sector. Many electrical components are installed in distribution system and generally the interruption will be occurred if one component is failure. Therefore, reliability of each component should be in the reasonable rage. The failure rate decreases over the working age of the components. The aging components are necessary to replace. On the other hand, the replacement cost also should be considered. A component is required to replace preventively upon reaching age, where the cost of preventive replacement is typically less than that of corrective replacement.
Moreover, reliability distribution is one of the main factors to estimate the optimal replacement time (OPT). Therefore, it is an important issue to forecast reliability accurately. Concerning this issue, the use of the average values is potentially misleading and it has two major drawbacks [1]. First, the average values cannot reflect the impact of relatively unreliable equipment and may overestimate or underestimate the reliability of customers. Secondly, the average values cannot reflect the impact of maintenance activities. Time varied failure rate for system components is introduced using random failure rate and Weibull distribution method in [2]. However, the 10 years of historical data is required for reliability analysis and it is not sufficient to estimate for the whole operating age of component such as 30 years, 40 years and so on. Moreover, the authors do not propose how to estimate the component’ reliability if the historical data is not available or for new components. Moreover, the failure rate is not considered based on the condition and working age of components.
Based on the problems and weak point mentioned above, we proposed how to evaluate the optimum replacement age using equipment inspection method and Weibull distribution method (WDM) considering cost of an unplanned on-line replacement and cost of a planned off-line replacement before failure. In this paper, time varied failure rate is evaluated based on equipment inspection method (EIM) with the condition score of equipment. Then, two parameters of Weibull distribution are figured out by regression method with the input failure data obtained from EIM. Thus, the equipment reliability and optimum replacement age is determined using constant-interval replacement model.
2. Methodlogy
2.1. Equipment Inspection Method
Three conditions of failure rate can be classified as best-condition, average-con- dition and worst-condition. These conditions will be changed accordance with condition and working ages of equipment. The condition of equipment is assigned between 0 and 1 by inspecting with inspection form. Generally, condition score is directly proportional to the working ages of equipment. Condition score zero refers to the best condition or new condition and one refers to the worst condition or damaged condition. The failure rates based on condition score can be calculated as follows [3].
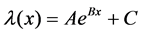 (1)
(1)
where, λ is failure rate and x is condition score. The parameters A, B, and Care computed as below.
 (2)
(2)
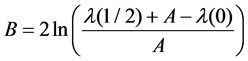 (3)
(3)
 (4)
(4)
where, 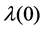 is the best-condition failure rate,
is the best-condition failure rate, 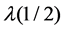 is the average-condi- tion failure rate, and
is the average-condi- tion failure rate, and  is the worst.
is the worst.
2.2. Weibull Distribution Method
The failure probability density function f(t), the failure probability distribution function F(t) and the reliability function R(t) can be analyzed using Weibull distribution methods [4].

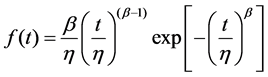 (5)
(5)
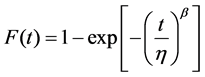 (6)
(6)

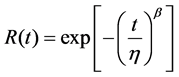 (7)
(7)
 (8)
(8)
where, η is a scale parameter and β is a shape parameter. These parameters can be calculated by using probability plot and regression analysis.
The x axis of Weibull plot is natural log value of life time or mean time to failure (MTTF)). The value of the y axis is calculated as shown in (9).

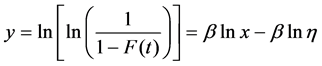 (9)
(9)
The proportion of the population that will fail by MTTF can be estimated by using median ranks method.
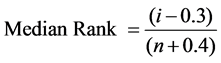 (10)
(10)
where, i is the adjusted rank and n is the total number of MTTF tested.
2.3. Optimum Replacement Time (OPT)
The OPT is to perform preventive replacements at constant intervals of length tp, irrespective of the age of the item. The objective is to determine the optimal interval between preventive replacements to minimize the total expected replacement cost per unit time. Cp is the total cost of a preventive replacement. Cf is the total cost of a failure replacement [5].
The total expected cost per unit time for preventive replacement at intervals of length tp denoted C(tp) is
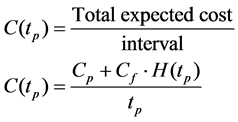 (11)
(11)
where, 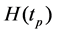 is the expected number of failures in interval (0,tp). Differentiating the right-hand side of (11) with respect to tp and equating it to zero gives the optimized results.
is the expected number of failures in interval (0,tp). Differentiating the right-hand side of (11) with respect to tp and equating it to zero gives the optimized results.
![]()
![]() (12)
(12)
After some differentiating process, we obtain
![]()
![]() (13)
(13)
In [6], the research has been conducted and proved that the expected failures in the period (0,tp) is equal to the probability f failure occurrence before time tp. Then,
![]() (14)
(14)
According to (8)
![]()
![]() (15)
(15)
The optimum replacement time and total expected cost per unit time become:
![]()
![]() (16)
(16)
![]() (17)
(17)
3. Test System
The test system used in this paper is RBTS Bus 2 system shown in Figure 1 [7]. The single 11 KV supply point for the RBTS Bus 2 is justified by the 20 MW load. The feeders are operated as radial feeders normally although they can be connected as a mesh.
The test system has four feeders and thirty six feeder sections. Two 33/11 kV transformers for substation and 11/0.4 kV transformers for load points are installed. Breakers also set up in substation and upstream area of every feeder. Disconnecting switches are located in feeder section 7, 21 and 32. Feeder types and lengths are listed in Table 1. The load data is listed in Table 2. The tie line effect is neglected in this paper.
The λ is the failure rate per year per mile for lines and the failure rate per year for other components. The reliability and system data is shown in Table 3. λ(0) is the best-condition failure rate, λ(1/2) is the average-condition failure rate and λ(1) is the worst-condition failure rate. These failure rate data is obtained from
![]()
Table 3. Reliability and system data.
[3].
The condition score of components to their operating years is described in Table 4. The score for transformer is obtained from [3] and the score for circuit breaker is from [8]. The condition score for other components are assumed based on their working principle.
4. Simulation Results
4.1. Variable Failure Rate Based on Condition Score
Using EIM as mentioned in (1), we can evaluate the different failure rate according to the respective condition score. Firstly, we need to find the parameters A, B and C using three types of failure rate for all components. Then, we can find MTTF for each working age. MTTF based on condition score for transformer is shown in Table 5 as an example. MTTF for every component in the system is necessary to evaluate using EIM.
Variable failure rate (VFR), average failure rate (AFR), worst failure rate and
![]()
Table 4. Age (year of operation) and condition score data.
![]()
Table 5. MTTF and condition score for power transformer.
best failure rate condition for circuit breaker can be seen in Figure 2. The lines are represented such as the best condition (Best), the worst condition (Worst), the average condition (Avg) and the variable failure rate (VFR).
For earlier working ages or until 0.5 condition score of circuit breaker, the AFR has over estimation compared with VFR as the value of AFR is higher than VFR. As we can see in figure, the red marker represents the value of VFR at condition score 0.5. The system operators or the utilities will set the maximum condition score and it is not reasonable to use the component until condition score 1. The failure rate at 0.06 failure/year is just for the accidently damaged condition of component. Moreover, they will try to maintain it almost at the best condition or failure rate at 0.005 failure/year. The maximum condition score for CB is set up at 0.75 and the highest failure rate is 0.03 failure/year.
4.2. Weibull Parameters
To estimate the reliability function with Weibull distribution, we need to find the shape parameter β, and scale parameter η. Weibull parameters can be easily calculated using regression analysis. MTTF is used as main input parameter for regression analysis. The MTTF is obtained based on VFR by using EIM method.
The result of regression analysis for transformer is shown in Figure 3. The
![]()
Figure 2. Comparison of failure rates for circuit breaker.
![]()
Figure 3. Regression analysis for pole mounted transformer.
parameters can be estimated from the trend line extracted from regression analysis. The shape parameter β is the slope of the trend line and the scale parameter η is represented to exp (-intercept of y/β). As in Figure 3, the slope is 1.145 and intercept is −12.965. Then, the scale parameter is 273. The parameters for all components are necessary to compute by regression analysis. The results are listed in Table 6.
4.3. Optimum Replacement Time
The optimal interval between preventive replacements is determined according to minimizing the total expected replacement cost per unit time. In this case, the ratio of Cp, the total cost of a preventive replacement, and Cf, the total cost of a failure replacement, has influence on tp, the optimum replacement time. The values of Cp and Cf will be changed corresponding to the equipment and the conditions. The cost ratio Cp/Cf, is commonly equal to 1/20. For some expensive system, the failure replacement cost is higher 100 times or more than the preventive replacement cost.
In Figure 4, the optimum replacement time for circuit breaker is evaluated based on the ratio of Cp/Cf. For example, Cf is 20 times more than Cp when Cp/Cf is 0.05. In this paper, the value of Cf is assumed as 20, 25, 30 and 35 times more than the value of Cp in four different estimations as the life span of circuit breaker is 30 years. Based on the simulation results, the optimum replacement time respective to the minimum cost can be seen in figures. In the case where the ratio is 0.0285, the value of the optimum replacement time is 26.07 years and the cost is 0.06557. As we can see, the optimal replacement time is longer whenever the failure replacement cost is higher.
The OPT for pole mounted transformer is figured out in Figure 5. In this estimation, the Cf is assumed as 25, 50, 75 and 100 times higher than Cp. If compared with circuit breaker, Cf of transformer is distinctly higher because more area will be interrupted and downtime will be longer when transformer is failed. The characteristic of the curves show that the OPT will be varied based on the value of Cp/Cf. The OPT is 54.2 years if Cf is 25 times higher than Cp. However, life span of transformer is only 40 years. Therefore, we can point out that Cf should not higher than 25 times of Cp.
The price of power transformer is relatively high and the Cf cannot be higher
![]()
Table 6. Weibull parameters for system’s component.
much than Cp as compared with circuit breaker or pole mounted transformer. Therefore, Cf is considered 1.5, 2, 5, and 7.5 times higher than Cp in Figure 6. If Cf is considered 10 or more than 10 times, the power transformer is about to replace within short time and it is not reasonable in practice. The OPT based on the ratio of Cp/Cf is forecasted as shown in figure. If Cf is less than 1.5 times of Cp, the OPT will be more than 30.16 years.
The reliability and failure distribution can be also checked at the optimum replacement time. In Figure 7, the reliability, failure distribution and expected
![]()
Figure 4. Optimum replacement time for CB.
![]()
Figure 5. Optimum replacement time for pole mounted transformer.
![]()
Figure 6. Optimum replacement time for power transformer.
![]()
Figure 7. Reliability, failure distribution and expected cost for CB.
cost per time is described as an example. In this example, the ratio of Cp/Cf is 0.05. The reliability probability is 0.8538 and failure probability is 0.1462 at the optimum replacement time of 39.8 years for CB.
5. Conclusions
This paper proposes how to estimate the optimum replacement time (OPT) by using combination of equipment inspection method, Weibull distribution method and the constant-interval replacement model for preventive maintenance. According to the results, the OPT is mainly depended on reliability probability of equipment and the ration of the total cost of a preventive replacement Cp and the total cost of a failure replacement Cf. Therefore, the estimation of OPT will be accurate if reliability and cost ratio is estimated. In this paper, the reliability estimation is more fact-based using EIM and WDM based on condition score. For the cost ratio, on the contrary, it is difficult to estimate the exact amount. In this paper, the cost ratio is considered in the possible range according to the life expectancy. Estimation of Cp and Cf will be a future consideration. However, in this paper, the OPT is evaluated based on different ratio of Cp and Cf. Consequently, reliability and failure probability can be checked respective to their OPT.
The proposed approach with corresponding computational methods in this paper can assist the system operators to make the economic maintenance and replacement decisions more easily.
Acknowledgements
This work was supported by Japan International Cooperation Agency.