Electrostatic Rayleigh-Taylor Mode in Electron-Positron-Ion Quantum Plasma ()
1. Introduction
Classical plasma is usually considered to have low densities and high temperature plasmas. But some technologies have made it possible to produce plasma having densities comparable to the solid state, and this type of plasma cannot be explained properly by using the laws of classical mechanic and therefore laws of quantum mechanics will be applied. Contrary to classical plasmas, quantum plasma exhibits the property of low temperature and high number density, and in nature there are many examples where such behavior of plasma is observed like in astrophysical environments e.g. in the crust of white dwarfs, brown dwarfs, Neutron stars and Magnatar etc. [1] [2] and in the core of giant planets (e.g. Jovian planets) [3] [4] . Dense quantum plasmas may also occur in the next generation of laser-based matter compression schemes [5] [6] [7] , in which the plasmon frequency is measurably shifted due to quantum effects. Other applications of dense quantum plasmas which are relevant to the collective dynamics of degenerate electrons/positrons include: the electron-hole plasma in quantum wires [8] , metallic nanostructures and thin films [9] , the dense quantum diode [10] , nanophotonics and nanowires [11] , nano-plasmonics [12] , high-gain quan- tum free-electron lasers [13] , quantum wells and piezomagnetic quantum dots [14] .
There are a few physically unlike results which may be marked “quantum”, first referable to distinguishability of the particles, and the equilibrium distribution then changes from the Maxwell-Boltzmann to the Fermi-Dirac. The inter- Fermion distance being smaller than the thermal de-Broglie wavelength in such cases, along with temperature degeneracy (a consequence of Pauli Exclusion Principle) and tunneling effects, give rise to new collective phenomena and the role of quantum corrections begins [15] . This also changes the dynamics by preventing two particles to be in the same state via exchange interaction. Second the particles will have the dispersive effects due which those particles are not located in phase space. Third some particles like electrons and positrons have an intrinsic magnetic moment or spin. The spin interacts with magnetic field via the dipole force thus affecting the dynamics [16] . There has recently been a surge in the interest of dense quantum plasmas for example see the Refs. [15] [17] - [25] . Altogether these studies include the effects of quantum corrections like Bohm? de Broglie potential, the zero temperature Fermi pressure and spin magnetization like properties which can significantly modify the dynamics of the plasma.
The above literatures mainly focus on perturbations in homogeneous quantum plasma backgrounds. However, some time quantum plasmas can have the non-uniform density features when brought into practice, which frequently occur in a real (e.g. in astrophysics) or effective (e.g. in inertial confined fusion) external gravitational field. The Rayleigh-Taylor (RT) instability is an important hydrodynamic effect that occurs at the plane interface between two fluids of different densities when a heavy fluid is accelerated into a lighter one. This type of instability for a fluid in a gravitational field was first investigated in his famous paper in 1882 by Rayleigh [26] and later Taylor in 1950 had applied it to all accelerated fluids [27] . Since then, this instability problem has been investigated by several investigators under varying assumptions [28] . The detailed description of this instability problem with other parameters and assumptions has been given e.g. in the Ref. [29] .
The hydrodynamic instabilities in quantum plasmas have been an important field of study of research in the last few years. Assuming a quantum hydrodynamic model for quantum plasmas, various authors have shown that the delicate interplay between dissipation and dispersion leads to a variety of instabilities like two stream instability, Kelvin-Helmholtz instability and Rayleigh-Taylor instability etc. [30] [31] [32] . The effect of quantum mechanism on the internal waves and the RT instability in plasma is considered by Vitaly in [32] . The effects of the quantum mechanism and magnetic field on electromagnetic mode of RT instability have been investigated in ideal incompressible plasma by deriving the linear growth rate in the presence of fixed boundary conditions [33] . The effect of quantum corrections on RT instability for a finite thickness layer of incompressible viscoelastic plasma through porous media was investigated recently in [34] . The RT instability in vertical/horizontal inhomogeneous rotating plasma with quantum effects is investigated by [35] [36] . The electrostatic RT instability is studied in a dense electron-ion quantum magnetoplasma [37] , where ions are assumed cold and classical while electrons are dense and quantum mechanical. It has shown that density gradient and quantum speed significantly modify the RT instability growth rate. Comparative to classical in the case of dense quantum magnetoplasma the RT instability linear growth rate is significantly higher and highly localized.
On the other side it is well known that electron-positron plasmas appear in the polar cap regions of pulsar magnetospheres, in the early universe, and in the inner region of the accretion disks surrounding the central black holes in active galactic nuclei, in the polar regions of neutron stars, at the center of our own galaxy, solar flares and have also been found in intense laser pulse propagating in plasmas [38] - [45] . However, some authors [46] [47] have suggested that electron-positron plasmas also contain a small fraction of heavy ions. Recent investigations [48] [49] 50] have shown some new and interesting linear and nonlinear phenomena in three component electron-positron-ion plasmas.
In this work we investigate the electrostatic RT mode by using the QHD model of quantum electron-positron-ion plasma. A dispersion relation is obtained under the assumption of drift density in homogeneity. The dispersion relation and growth rate of instability are studied by using the Cardano’s method of solving the cubic equation.
2. Basic Formulation and Governing Equations
Consider an electron-positron-ion (e-p-i) plasma with magnetic field , where
, where 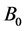 is the external magnetic field. In equilibrium condition density gradient and gravitational field presumably in opposite direction i.e.
is the external magnetic field. In equilibrium condition density gradient and gravitational field presumably in opposite direction i.e.  and
and . This shows the fact that density and gravitational field is along x-axis and magnetic field applied from external source is along z-axis. Electric field and wave propagation are taking place along y- axis i.e.
. This shows the fact that density and gravitational field is along x-axis and magnetic field applied from external source is along z-axis. Electric field and wave propagation are taking place along y- axis i.e. 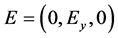 and
and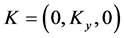 . In order to study the RT-instability in quantum e-p-i plasma, we use the following linearized quantum magneto hydrodynamic equations i.e. momentum equation
. In order to study the RT-instability in quantum e-p-i plasma, we use the following linearized quantum magneto hydrodynamic equations i.e. momentum equation
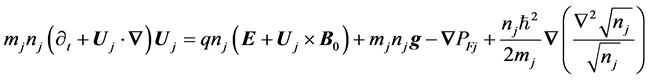 (1)
(1)
The continuity equation
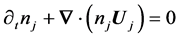 (2)
(2)
where q, 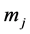 , g,
, g,  and
and  are electrostatic charge, particle mass, acceleration due to gravity, density and velocity of the jth species respectively, where “j” represents electron, positron and ion respectively. The quasi-neutrality condition in equilibrium reads
are electrostatic charge, particle mass, acceleration due to gravity, density and velocity of the jth species respectively, where “j” represents electron, positron and ion respectively. The quasi-neutrality condition in equilibrium reads 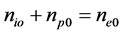 and ħ is the Plank constant divided by
and ħ is the Plank constant divided by , and e is electronic charge. The quantum force term i.e. the last two terms of Equation (1) are appearing due to quantum mechanical effects of jth species and denote the quantum correlation between density fluctuations and the temperature degeneracy factor due to Fermi-Dirac statistics. The equation of state for
, and e is electronic charge. The quantum force term i.e. the last two terms of Equation (1) are appearing due to quantum mechanical effects of jth species and denote the quantum correlation between density fluctuations and the temperature degeneracy factor due to Fermi-Dirac statistics. The equation of state for
degenerate electrons and positron is  known as Fermi pressure and the pressure gradient force
known as Fermi pressure and the pressure gradient force  with
with 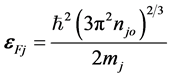 is being the jth Fermi energy on the Fermi surface. The quantum mechanical effects for ions are neglected due to large mass of ions compared to electrons and positrons we assume. Thus Equation (1) for cold streaming ions in linearized form can be written as
is being the jth Fermi energy on the Fermi surface. The quantum mechanical effects for ions are neglected due to large mass of ions compared to electrons and positrons we assume. Thus Equation (1) for cold streaming ions in linearized form can be written as
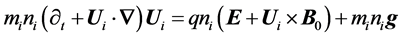 (3)
(3)
In the equilibrium state, we find the ions drift as
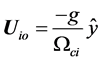 (4)
(4)
where ![]() is known as ion cyclotron frequency. The electrons and positrons have drifts (opposite and parallel) but can be neglected in the limit
is known as ion cyclotron frequency. The electrons and positrons have drifts (opposite and parallel) but can be neglected in the limit![]() . The equation of motion for Fermionic electron/positron is
. The equation of motion for Fermionic electron/positron is
![]() (5)
(5)
![]() (6)
(6)
Following the procedure given in [51] for low frequency ![]() electrostatic perturbations, the perpendicular first order components of the ion fluid velocity can be obtained as
electrostatic perturbations, the perpendicular first order components of the ion fluid velocity can be obtained as
![]() (7)
(7)
where ![]() represents
represents ![]() drift while
drift while ![]() is the polarization drift of ion. Further simplification of
is the polarization drift of ion. Further simplification of ![]() and
and ![]() gave
gave
![]() (8)
(8)
![]() (9)
(9)
In the above equations ![]() represents the ions streaming fluid velocity. Since polarization drift directly proportional to inertia, so compare to ions, it can be neglected for both electrons and positrons, therefore, from Equation (5) the perpendicular component of velocity vector for quantum mechanical and Fermionic electron is
represents the ions streaming fluid velocity. Since polarization drift directly proportional to inertia, so compare to ions, it can be neglected for both electrons and positrons, therefore, from Equation (5) the perpendicular component of velocity vector for quantum mechanical and Fermionic electron is
![]() (10)
(10)
Similarly the perpendicular component of positron, from Equation (6) is
![]() (11)
(11)
Due to the absence of polarization drift, electron and positron streaming terms are not appearing in Equations (10) and (11). In linearized form the continuity equations for ions, electrons and positrons are
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
All the above Equations (7)-(13) are valid for long wavelength limit, i.e.![]() , where
, where ![]() is the Fermi length of electron and positron. Also we have assumed that phase speed of electrostatic RT mode is greater than quantum Bohm potential speed and much smaller than the Fermi speed of electron and
is the Fermi length of electron and positron. Also we have assumed that phase speed of electrostatic RT mode is greater than quantum Bohm potential speed and much smaller than the Fermi speed of electron and
positron i.e.![]() . We have neglected the terms
. We have neglected the terms ![]() and
and
![]() in Equations (13) and (14) by assuming that constant streaming velocities of electron and positron are not spatial functions. Assuming a plane wave solution of the form
in Equations (13) and (14) by assuming that constant streaming velocities of electron and positron are not spatial functions. Assuming a plane wave solution of the form ![]() to all the perturbed quantities and using the drift approximation
to all the perturbed quantities and using the drift approximation![]() , we obtain the number density for ions as
, we obtain the number density for ions as
![]() (15)
(15)
where ![]() is known as Doppler shifted frequency and
is known as Doppler shifted frequency and ![]() is the inverse inhomogeneity scale length for ions. The electron continuity Equation (13) leads to the perturbed electron density as
is the inverse inhomogeneity scale length for ions. The electron continuity Equation (13) leads to the perturbed electron density as
![]() (16)
(16)
where ![]() is the inverse inhomogeneity scale length for electrons, and
is the inverse inhomogeneity scale length for electrons, and ![]() is the quantum corrected modified diamagnetic drift velocity of electrons with
is the quantum corrected modified diamagnetic drift velocity of electrons with ![]() is the modified quantum ion acoustic velocity due to electron and
is the modified quantum ion acoustic velocity due to electron and ![]() is the well-defined quantum ion acous-
is the well-defined quantum ion acous-
tic speed. Similarly, if Equation (14) is utilized to determine the density of positron by employing the same procedure as used for finding the density of electron we have the following relation
![]() (17)
(17)
With ![]() is being the inverse inhomogeneity scale length for positron, and
is being the inverse inhomogeneity scale length for positron, and ![]() is the quantum corrected modified diamagnetic drift velocity of positron with
is the quantum corrected modified diamagnetic drift velocity of positron with ![]() is another modified quantum ion acoustic speed due to positron.
is another modified quantum ion acoustic speed due to positron.
2.1. Dispersion Relation and ERT Instability
Under the assumption kλFp≪1 we can write the perturbed quasi neutrality condition
![]() (18)
(18)
instead of Poisson equation. Using Equations (15)-(17) in Equation (18) leads to a generalized dispersion relation as
![]() (19)
(19)
Here ![]() represents the ratio of positron to electron. If we ignore the positron concentration i.e.
represents the ratio of positron to electron. If we ignore the positron concentration i.e. ![]() then we get exactly dispersion relation of RT in electron-ion quantum magneto plasma of [37] i.e.
then we get exactly dispersion relation of RT in electron-ion quantum magneto plasma of [37] i.e.
![]() (20)
(20)
In order to discuss the instability analysis by incorporating the streaming of ions, we solve Equation (19) in detail and arrive to the following form
![]() (21)
(21)
Introducing gravitational field![]() , the above equation in cubic form can be written
, the above equation in cubic form can be written
![]() (22)
(22)
where the constants a, b and c all are real and are defined as
![]() (23)
(23)
Employing the following normalized parameters
![]() ,
,![]() ,
,
![]() ,
, ![]() ,
, ![]()
The above Equations (22) and (23) in normalized form can be written as
![]() (24)
(24)
![]()
![]()
![]()
![]()
Here the normalized Bohm parameter ![]() represents the ratio of plasmon energy to Fermi energy and
represents the ratio of plasmon energy to Fermi energy and ![]() is the electron Fermi length while
is the electron Fermi length while ![]() shows the ion-sound gyro-radius. Equation (24) is the normalized dispersion relation. Let us consider a simple case where
shows the ion-sound gyro-radius. Equation (24) is the normalized dispersion relation. Let us consider a simple case where ![]() which makes the
which makes the ![]() term to be negligible in Equation (24) and hence
term to be negligible in Equation (24) and hence
![]() (25)
(25)
This is quadratic equation and instability will occur when ![]() (we shall omit the notation for simplicity). We use
(we shall omit the notation for simplicity). We use ![]() (where
(where ![]() is the real frequency of the wave mode and
is the real frequency of the wave mode and ![]() the growth rate) in Equation (25) and solve it we get
the growth rate) in Equation (25) and solve it we get
![]() (26)
(26)
It is clear that quantum mechanical effects depend on the particle number density, so using the data of neutrons stars, magnetars and white dwarfs (as mentioned in Results and discussion section), Figure 1 shows the plot of normalized real frequency ![]() versus the normalized wave number
versus the normalized wave number ![]() for different values of positron concentration i.e.
for different values of positron concentration i.e. ![]() (solid line) and
(solid line) and ![]() (dashed line). It is seen that the electrostatic R-T mode is well separated. The growth rate γ of the propagating wave is depicted in Figure 2 for different values of positron concentration i.e.
(dashed line). It is seen that the electrostatic R-T mode is well separated. The growth rate γ of the propagating wave is depicted in Figure 2 for different values of positron concentration i.e. ![]() (solid line) and
(solid line) and ![]() (dashed line). It is obvious that γ increases for low wave numbers
(dashed line). It is obvious that γ increases for low wave numbers![]() , till a threshold wave number
, till a threshold wave number![]() , then γ decreases and the system tends to have less instability. The growth rate γ
, then γ decreases and the system tends to have less instability. The growth rate γ
is affected by the positron concentration and in fact decreases with respect to![]() . Therefore, the number of positrons would lead to lower the instability of R-T mode in electron-positron-ion system.
. Therefore, the number of positrons would lead to lower the instability of R-T mode in electron-positron-ion system.
2.2. Instability Analysis by Cardano’s Method
The Cardano’s formula (named after Girolamo Cardano 1501-1576), which is similar to the perfect-square method to quadratic equations, is a standard way to find a real root of a cubic equation. It provides a technique for solving the general cubic equation in terms of radicals. The other two roots (real or complex) can be found by polynomial division and the quadratic formula. The solution has two steps. We first “depress” the cubic equation and then solve the depressed equation.
By using the Cardano’s method of solving the cubic equation, we will discuss the RT instability analysis of Equation (24). In order to address the instability process, again ![]() (where
(where ![]() is being the real frequency of wave mode and
is being the real frequency of wave mode and ![]() is the growth rate) in Equation (25) and solve it for that
is the growth rate) in Equation (25) and solve it for that ![]() we get real and imaginary parts as (we shall omit again the notation for simplicity)
we get real and imaginary parts as (we shall omit again the notation for simplicity)
![]() (27)
(27)
![]() (28)
(28)
For the solution of cubic equation here we use Cardano’s method: by introducing ![]() also by defining the term p and q as
also by defining the term p and q as ![]() and
and ![]() the equation (27) then reduces to reduced cubic equation having no second degree term i.e.
the equation (27) then reduces to reduced cubic equation having no second degree term i.e.
![]() (29)
(29)
If ![]() and
and ![]() are zero, then
are zero, then ![]() is zero. Otherwise, we can consider the cases when the value of
is zero. Otherwise, we can consider the cases when the value of ![]() or
or ![]() is zero and when both aren’t zero. We will consider the case when both these are not zero. Consider, that, for two numbers u and v: if
is zero and when both aren’t zero. We will consider the case when both these are not zero. Consider, that, for two numbers u and v: if![]() ,
, ![]() and
and ![]() then solving for
then solving for ![]() and v we have
and v we have
![]() (30)
(30)
By finding the values of u and v, we will be able to solve the cubic.
![]() (31)
(31)
The nature of the Cardano roots can be described with the help of the discriminant Δ as follow.
1. If![]() , then all the roots are real, and at least two are equal.
, then all the roots are real, and at least two are equal.
2. If![]() , then
, then ![]() is a real number, and so one root (the principal root) is real, and the other two are complex numbers.
is a real number, and so one root (the principal root) is real, and the other two are complex numbers.
3. If![]() , then
, then ![]() is imaginary, so all the roots are real, and u and v will be complex numbers. This is the so called irreducible case. We will consider case (2) and (3) only.
is imaginary, so all the roots are real, and u and v will be complex numbers. This is the so called irreducible case. We will consider case (2) and (3) only.
For case (2), Δ is not negative, so the square root is a real number. In this case the real root is determined as
![]() (32)
(32)
The other two roots are complex and of no interest. Regarding to this real root we have the following growth rate for RT instability
![]() (33)
(33)
For case (3), since ![]() and
and![]() , so in this case
, so in this case ![]() is an imaginary number i.e.
is an imaginary number i.e. ![]() which implies that
which implies that
![]()
Using the trigonometry concept of complex analysis we find the following three normalized real roots of RT mode
![]() (34)
(34)
![]() (35)
(35)
![]() (36)
(36)
where ![]() and
and![]() . The corresponding three normalized growth rates for R-T instability are as follow
. The corresponding three normalized growth rates for R-T instability are as follow
![]() (37)
(37)
![]() (38)
(38)
![]() (39)
(39)
One out of these three modes will be growing, which will determine the R-T instability growth rate.
3. Result and Discussion
To see the complete view of quantum effects that include the tunneling through Bohm potential and the Pauli-exclusion principle through the Fermi degenerate pressure on the growth rate of R-T instability (31)-(38) along with coefficients are numerically analyzed. For numerical scheme we may use values given in [52] for a typical white dwarf with number density ![]() and
and ![]() [53] . Other physical parameters in cgs system are given as
[53] . Other physical parameters in cgs system are given as![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() . It should be noted that all the above equations are in dimensionless form.
. It should be noted that all the above equations are in dimensionless form.
3.1. Analysis of R-T Instability of Equation (33)
In this particular case, the growth rate (33) is based on the real frequency (32) that explicates the RT instability in electron-positron-ion quantum plasma. Using the above-mentioned data in normalized coefficients of Equation (24) the normalized growth rate (33) is plotted for electrostatic RT mode of instability with effects of density, and ambient magnetic field variation (Figure 3 and Figure 4). It is observed from all these three figures that the growth rate is damping, which means that inhomogeneity in plasma here acts as sink and taking energy from perturbation. The consequence of such analysis (i.e. damping phenomena) in nonlinear regime then gives shocks in such system which is beyond from the scope of present study. It is shown in Figure 3, and Figure 4 that the damping rate increases with increasing density, and decreases with respect to B₀. This means that increased density acts like source of sink and absorbs energy from perturbation while with B₀ opposite effects occurred.
3.2. Analysis of R-T Instability of Equations (37)-(39)
Using the Cardano method of solving the cubic Equation (27) for the condition where all the roots are real and different, we then get the real mode of Equations (34)-(36) and regarding to that we get three growth rates Equations (37)-(39), for ERT instability. Using the above-mentioned data the normalized growth rate (37) is diagrammed for RT mode of instability with effects of electron density, and ambient magnetic field as shown in Figure 5 and Figure 6. Figure 5 and Figure 6 show that the growth rate increases (decreases) with increasing
number density (magnetic field B₀). Thus magnetic field B₀ suppresses the instability as it confines the particles more in the center than at periphery for localized mode. Also the frequency of wave mode is less than![]() , so by increasing B₀ makes this comparison more obvious and hence decreases the growth rate. On the other hand by increasing the number density of electrons makes the plasma more dense and shrinks which means more particles are available to give
, so by increasing B₀ makes this comparison more obvious and hence decreases the growth rate. On the other hand by increasing the number density of electrons makes the plasma more dense and shrinks which means more particles are available to give
energy to wave perturbation as![]() . This consequently increases the growth
. This consequently increases the growth
rates and makes the RT mode unstable. Similarly the stabilizing effect of the positron concentration on growth rate variation (37) is demonstrated in Figure 7, which shows that the growth rate of RT instability decreases with respect to ![]() variation. It indicates that positron concentration plays a stabilizing role in the instability analysis. It means that growth rate decreases with increased values of
variation. It indicates that positron concentration plays a stabilizing role in the instability analysis. It means that growth rate decreases with increased values of![]() .
.
The similar behavior of growth rate as of Figure 7 is shown in Figure 8 for second root (Equation (38)) with variation of positron concentration. It signifies that growth rate decreases with increased values of![]() . Similarly Figure 9 and Figure 10 respectively exhibit the growth rate variation of second root (Equation (38)) for different values of electron density and magnetic field B₀. These two figures demonstrate that the growth rate increases (decreases) with increasing number density (magnetic field B₀). The growth rate variation of the second root is of standard trend and shows the same behavior as mentioned in different literature. The third root (Equation (39)) shows a damping trend.
. Similarly Figure 9 and Figure 10 respectively exhibit the growth rate variation of second root (Equation (38)) for different values of electron density and magnetic field B₀. These two figures demonstrate that the growth rate increases (decreases) with increasing number density (magnetic field B₀). The growth rate variation of the second root is of standard trend and shows the same behavior as mentioned in different literature. The third root (Equation (39)) shows a damping trend.
4. Summary and Conclusion
To summarize, we have analytically and numerically studied the Rayleigh Taylor instability in quantum E-P-I magneto plasma whose constituents are the electrons and positrons with fraction of ions. We have used the quantum hydrody-
namic equation where ions were dealt cold and classical while electron and positron are considered inertialess and quantum mechanical with their respective Fermi temperatures. General dispersion relation for RT instability was deduced, under the drift approximation. The presence of positron makes the algebraic equation a cubic one. In simplified form the real and growth rate of RT mode was discussed with effect of positron concentration. The Cardano’s method of solving the cubic equation was used to deduce the real and imaginary roots of RT instability. The real part of wave gives the dispersion relation and the imaginary one defines the growth rate of the RT mode. The growth rate of RT instability is examined in detail with essence of pair plasma density and magnetic field variation. It is found that quantum speed and density gradient have modified the RT instability significantly. It was shown that the growth rate of Rayleigh-Taylor instability in E-P-I quantum plasma increases with increasing of electron density while decreasing with increasing of magnetic field ![]() and positron concentration. We have discussed the examples of celestial body (like white dwarf) that suggests the presence of RT instability in electron-positron-ion quantum magneto plasma.
and positron concentration. We have discussed the examples of celestial body (like white dwarf) that suggests the presence of RT instability in electron-positron-ion quantum magneto plasma.