The Cost Functional and Its Gradient in Optimal Boundary Control Problem for Parabolic Systems ()
1. Introduction
Many researches in recent years have been devoted to the studies of optimal control problems for a distributed parameter system. Optimal control is widely applied in aerospace, physics, chemistry, biology, engineering, economics and other areas of science and has received considerable attention of researchers.
The optimal boundary control problem for parabolic systems is relevant in mathematical description of several physical processes including chemical reactions, semiconductor theory, nuclear reactor dynamics, population dynamics [1] and [2] . The partial differential equations involved in these problems include elliptic equations, parabolic equations and hyperbolic equations [3] [4] .
Optimization can be of constrained or unconstrained problems. The presence of constraints in a nonlinear programming creates more problems while finding the minimum as compared to unconstrained ones. Several situations can be identified depending on the effect of constraints on the objective function. The simplest situation is when the constraints do not have any influence on the minimum point. Here the constrained minimum of the problem is the same as the unconstrained minimum, i.e., the constraints do not have any influence on the objective function. For simple optimization problems it may be possible to determine, beforehand, whether or not the constraints have any influence on the minimum point. However, in most of the practical problems, it will be extremely difficult to identify it. Thus one has to proceed with general assumption that the constraints will have some influence on the optimum point. The minimum of a nonlinear programming problem will not be, in general, an extreme point of the feasible region and may not even be on the boundary. Also the problem may have local minima even if the corresponding unconstrained problem is not having local minima. Furthermore, none of the local minima may correspond to the global minimum of the unconstrained problem. All these characteristics are direct consequences of the introduction of constraints and hence we should to have general algorithms to overcome these kinds of minimization problems [5] [6] [7] [8] [9] .
The algorithms for minimization are iterative procedures that require starting values of the design variable x. If the objective function has several local minima, the initial choice of x determines which of these will be computed. There is no guaranteed way of finding the global optimal point. One suggested procedure is to make several computer runs using different starting points and pick the best Rao [10] . The majority of available methods are designed for unconstrained optimization, where no restrictions are placed on the de-sign variables. In these problems the minima, if they exist are stationary points (points where gradient vector of the objective function vanishes). There are also special algorithms for constrained optimization problems, but they are not easily accessible due to their complexity and specialization.
All of the many methods available for the solution of a constrained nonlinear programming problem can be classified into two broad categories, namely, the direct methods and the indirect methods approach. In the direct methods the constraints are handled in an explicit manner whereas in the most of the indirect methods, the constrained problem is solved as a sequence of unconstrained minimization problems or as a single unconstrained minimization problem. Here we are concerned on the indirect methods of solving constrained optimization problems. A large number of methods and their variations are available in the literature for solving constrained optimization problems using indirect methods. As is frequently the case with nonlinear problems, there is no single method that is clearly better than the others. Each method has its own strengths and weaknesses. The quest for a general method that works effectively for all types of problems continues. Sequential transformation methods are the oldest methods also known as Sequential Un-Constrained Minimization Techniques (SUMT) based upon the work of Fiacco and McCormick, 1968. They are still among the most popular ones for some cases of problems, although there are some modifications that are more often used. These methods help us to remove a set of complicating constraints of an optimization problem and give us a frame work to exploit any available methods for unconstrained optimization problems to solve, perhaps, approximately. [5] [6] [7] [8] [9] . However, this is not without a cost. In fact, this transforms the problem into a problem of non-smooth (in most cases) optimization which has to be solved iteratively. The sequential transformation method is also called the classical approach and is perhaps the simplest to implement. Basically, there are two alternative approaches. The first is called the exterior penalty function method (commonly called penalty method), in which a penalty term is added to the objective function for any violation of constraints. This method generates a sequence of infeasible points, hence its name, whose limit is an optimal solution to the original problem. The second method is called interior penalty function method (commonly called barrier method), in which a barrier term that prevents the points generated from leaving the feasible region is added to the objective function. The method generates a sequence of feasible points whose limit is an optimal solution to the original problem. Luenberger [11] illustrated that penalty and barrier function methods are procedures for approximating constrained optimization problems by unconstrained problems.
In the meanings of constrained conditions, these optimal control problems can be divided into control con-strained problems and state constrained problems. In each of the branches referred above, there are many excellent works and also many difficulties to be solved.
The rest of this paper is organized as follows. In Section 2, the proposed system of optimal control problem with respect to a parabolic equation is offered. Section 3 describes the analysis of existence and uniqueness of the solution of the POCP. In Section 4, the variation of the functional and its gradient is presented. Section 5 describes Lipschitz continuity of the gradient cost functional. Finally, conclusions are presented in Section 6.
2. Problem Statement
Consider the following POCP process be described in:
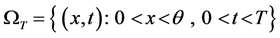 :
:
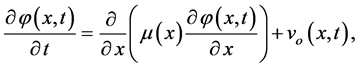 (1)
(1)
with the initial and the boundary conditions:
 (2)
(2)
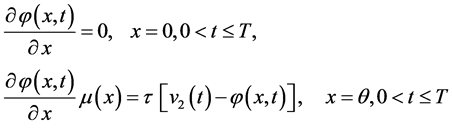 (3)
(3)
where the solution of the problem (1-3) is , since,
, since, 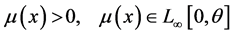 , the coefficient of convection
, the coefficient of convection 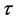 is positive constant-sometimes
is positive constant-sometimes 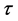 is called coefficient of heat transfer. The admissible controls is a set
is called coefficient of heat transfer. The admissible controls is a set 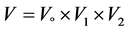 defined as
defined as
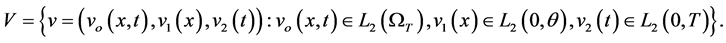
Many physical and engineering settings have the mathematical model (1-3), in particular in hydrology, material sciences, heat transfer and transport problems [12] . In the case of heat transfer, the Robin condition physically is realized as follows. Let the surface  of the rod be exposed to air or other fluid with temperature. Then
of the rod be exposed to air or other fluid with temperature. Then  is the temperature difference at
is the temperature difference at  between the rod and its surroundings. According to Newton’s law of cooling, the rate at which heat is transferred from the rod to the fluid is proportional to the difference in the temperature between the rod and the fluid, i.e.
between the rod and its surroundings. According to Newton’s law of cooling, the rate at which heat is transferred from the rod to the fluid is proportional to the difference in the temperature between the rod and the fluid, i.e.
 (4)
(4)
The purpose is to find the optimal control  that minimizes the following cost functional:
that minimizes the following cost functional:
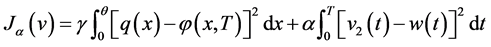 (5)
(5)
and
 (6)
(6)
where 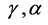 are given positive numbers,
are given positive numbers, ![]() is given function from
is given function from ![]() ,
, ![]() is given function from
is given function from ![]() with
with ![]() is a fixed time. Penalty function methods are the most popular constraint handling methods among users. Two main branches of penalty method have been proposed in the literature: Exterior and Interior which is also called the barrier method. The basic idea in penalty method is to eliminate some or all constraints and add to the objective function a penalty term which prescribes a high cost to infeasible points. Associated with this method is a parameter
is a fixed time. Penalty function methods are the most popular constraint handling methods among users. Two main branches of penalty method have been proposed in the literature: Exterior and Interior which is also called the barrier method. The basic idea in penalty method is to eliminate some or all constraints and add to the objective function a penalty term which prescribes a high cost to infeasible points. Associated with this method is a parameter![]() , which determines the severity of penalty and as a consequence the extent to which the resulting unconstrained problem approximates the original constrained problem. We restrict attention to the polynomial order-even penalty function. The constrained optimal control problem (5-6) is converted to unconstrained optimal control pro- blem by adding a penalty function [13] to the cost functional (5), yielding the modified function:
, which determines the severity of penalty and as a consequence the extent to which the resulting unconstrained problem approximates the original constrained problem. We restrict attention to the polynomial order-even penalty function. The constrained optimal control problem (5-6) is converted to unconstrained optimal control pro- blem by adding a penalty function [13] to the cost functional (5), yielding the modified function:
![]() (7)
(7)
where![]() ,
, ![]() ,
, ![]() and
and![]() ,
, ![]() ,
,![]() .
.
3. Well-Posedness of System
This section present the concept of the weak solution of the system (1-3) and the existence solution. Let a function ![]() of the weak solution of the problem, and satisfies the following integral, for all
of the weak solution of the problem, and satisfies the following integral, for all![]() :
:
![]() (8)
(8)
The weak solution ![]() of the direct problem exists and unique under the above conditions with respect to the given data [14] [15] . According to [12] , the solution of the optimal control problem can be defined as a solution of the minimization problem for the cost functional
of the direct problem exists and unique under the above conditions with respect to the given data [14] [15] . According to [12] , the solution of the optimal control problem can be defined as a solution of the minimization problem for the cost functional ![]() under condition (6), given by (5):
under condition (6), given by (5):
![]() (9)
(9)
Theorem 1:
Under the above conditions, the optimal control problem has an optimal solution ![]() in
in![]() .
.
Proof: when![]() , the solution
, the solution ![]() is a strict solution of systems (1-3) and (5-6), where
is a strict solution of systems (1-3) and (5-6), where ![]() satisfies the equation of functional,
satisfies the equation of functional,
![]() . In parabolic problems and according to the theory of weak solution, can prove that the sequence
. In parabolic problems and according to the theory of weak solution, can prove that the sequence ![]() weakly con-
weakly con-
verges to the function![]() , so that the traces sequence
, so that the traces sequence ![]() of corresponding solutions of system (1-3) converges to the solution
of corresponding solutions of system (1-3) converges to the solution ![]() in
in![]() , hence, when n→∞ then
, hence, when n→∞ then ![]() [16] . Therefore the func-
[16] . Therefore the func-
tional ![]() is weakly continuous on V, and the non-empty set of solutions
is weakly continuous on V, and the non-empty set of solutions ![]() for the minimization problem (5-6) [17] .
for the minimization problem (5-6) [17] .
4. The Variation of the Functional and Its Gradient
The main objective here, the proof of Theorem 2 (found in tail of this section) which requires the following two lemmas; lemma 1 and lemma 2. Let the first variation of the cost functional ![]() of the cost functional (7) as follows:
of the cost functional (7) as follows:
![]() (10)
(10)
therefore,
![]() (11)
(11)
where
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Therefore the function ![]() is the solution of the following system:
is the solution of the following system:
![]() (12)
(12)
Lemma 1:
If the direct system (1-3) have the corresponding solution ![]() and
and ![]() is the solution of the adjoint parabolic problem [18] :
is the solution of the adjoint parabolic problem [18] :
![]() (13)
(13)
then the following integral identity holds for all elements ![]() and
and ![]() :
:
![]() (14)
(14)
Proof: At ![]() with the condition in (13) to transform the left-hand side of (14) as follows:
with the condition in (13) to transform the left-hand side of (14) as follows:
![]()
At the boundary conditions in (13) and (14) for the functions ![]() and
and![]() ; we obtain (14). Corresponding to the inverse problem in system (1-3) and (5-6), the parabolic problem (13) define as an adjoint problem. By backward one of the Equation (13), the “final condition” at
; we obtain (14). Corresponding to the inverse problem in system (1-3) and (5-6), the parabolic problem (13) define as an adjoint problem. By backward one of the Equation (13), the “final condition” at ![]() it is a well- posed initial boundary-value problem under a time reversal. The first variation of the cost functional
it is a well- posed initial boundary-value problem under a time reversal. The first variation of the cost functional ![]() obtain by using integral identity in (14) on the right-hand side of Equation (11):
obtain by using integral identity in (14) on the right-hand side of Equation (11):
![]() (15)
(15)
Using the definition of the Fréchet-differential and the above the scalar product definition in V, transform the right-hand side of (15) need into the following expression:
![]() (16)
(16)
Now we need to show that the last two terms on the right-hand side of (15) are of order![]() , with
, with![]() .
.
Lemma 2:
If the parabolic problem (12) have the solution![]() ,
, ![]() , then the following inequality holds:
, then the following inequality holds:
![]() (17)
(17)
where ![]() is the norm
is the norm ![]() of the function
of the function![]() ,
, ![]() is the norm
is the norm ![]() of the function
of the function![]() , and the constants
, and the constants![]() ,
, ![]() are defined as follows:
are defined as follows:
![]() (18)
(18)
Proof:
Multiplying the Equation (12) by![]() , then integrating the result on
, then integrating the result on![]() ,
, ![]() ,
,![]() .
.
We obtain energy identity after applying the initial and boundary conditions as the following:
![]() (19)
(19)
We use the ![]() -inequality
-inequality ![]() for the solution
for the solution ![]() of the parabolic problem (19). Then for all
of the parabolic problem (19). Then for all ![]() we have:
we have:
![]() (20)
(20)
Applying the Cauchy inequality to estimate the term![]() :
:
![]()
By integrating the both sides of above inequality on![]() , we obtain:
, we obtain:
![]() (21)
(21)
and use this estimate on the right-hand side of (20):
![]()
From (19) with above inequality, we obtain:
![]() (22)
(22)
where ![]() and
and![]() , we get bound (18) with
, we get bound (18) with ![]() for estimate (22):
for estimate (22):
![]()
Hence, the last integral (15) is bounded by ![]() and using Fréchet- differential definition at
and using Fréchet- differential definition at![]() .
.
![]()
we obtain the following theorem:
Theorem 2:
The cost functional ![]() is Fréchet-differentiable in the considered problem hold, and Fréchet derivative at
is Fréchet-differentiable in the considered problem hold, and Fréchet derivative at ![]() of
of ![]() can be defined by the solution
can be defined by the solution ![]() of the adjoint problem (13) as follows:
of the adjoint problem (13) as follows:
![]() (23)
(23)
5. The Continuity of Gradient Functional
In this section, by helping the gradient of cost functional ![]() we prove the Lipschitz continuity of
we prove the Lipschitz continuity of![]() . The minimization problem (9) need an estimation of the iteration parameter
. The minimization problem (9) need an estimation of the iteration parameter ![]() beginning with the initial iteration
beginning with the initial iteration ![]() :
:
![]() (24)
(24)
In many situation estimations of determine the parameter ![]() in various gradient methods is a difficult problem [19] . However, for arbitrary parameters
in various gradient methods is a difficult problem [19] . However, for arbitrary parameters![]() , the parameter
, the parameter ![]() can be estimated via the Lipschitz constant in the case of Lipschitz continuity of the gradient
can be estimated via the Lipschitz constant in the case of Lipschitz continuity of the gradient ![]() as follows:
as follows:
![]() (25)
(25)
Lemma 3:
The functional ![]() is of Hölder class
is of Hölder class ![]() under the conditions of Theorem 2 and
under the conditions of Theorem 2 and
![]() (26)
(26)
where
![]() (27)
(27)
where ![]() and for parameters
and for parameters![]() ,
, ![]() , the Lipschitz constant is defined in (22) as follows:
, the Lipschitz constant is defined in (22) as follows:
![]() (28)
(28)
Proof: Let the following backward parabolic problem
![]() (29)
(29)
has the solution![]() . Therefore, using the initial and boundary conditions after multiplying both sides of Equation (29) by
. Therefore, using the initial and boundary conditions after multiplying both sides of Equation (29) by![]() , and integrating on
, and integrating on ![]() as in the proof of Lemma 2, we can get the following energy identity:
as in the proof of Lemma 2, we can get the following energy identity:
![]() (30)
(30)
implies the following two inequalities:
![]() (31)
(31)
and
![]() (32)
(32)
Multiplying the first and the second inequality by ![]() and
and![]() , correspondingly, summing up them, and then using the inequality (20) we obtain:
, correspondingly, summing up them, and then using the inequality (20) we obtain:
![]() (33)
(33)
Computing of the second integral on the right-hand side of (26) by the same term. From the energy identity (30) we can obtain the following:
![]() (34)
(34)
This, with the last estimate, concludes
![]() (35)
(35)
where![]() , using this in (27) and taking into account Lemma 2 we obtain (26) with the Lipschitz constant
, using this in (27) and taking into account Lemma 2 we obtain (26) with the Lipschitz constant ![]() in (28).
in (28).
6. Conclusion
In this paper, we studied a class of the constrained OCP for parabolic systems. The existence and uniqueness of the system is introduced. In this way, the uniqueness theorem for the solving POCP is introduced. Therefore, a theorem for the sufficient differentiability conditions has been proved. By using the exterior penalty function method, the constrained problem is converted to new unconstrained OCP. The common techniques of constructing the gradient of the cost functional using the solving of the adjoint problem is investigated.