1. Introduction
“The state of matter that would admit photon-matter equilibrium under such conditions is a mystery.” [1]
Figure 1 shows the luminous cloud of bubbles that is formed in the liquid by ultrasound. This phenomenon of sonoluminescence (SL) has been known for 80 years. Generated by ultrasound, bubbles are a result of cavitation in the liquid. The cavitation may be caused in other ways, for example, by rotating the screw. The glow also occurs at this cavitation―cavitational luminescence (CL). Lord Rayleigh discovered the phenomenon of cavitation a hundred years ago.
Today it is clear why the cavitational bubbles in liquids are formed, but it is still unclear why they glow. Attempts to explain this experimental phenomenon, for example, by the formation of plasma inside the bubble, lead to the fact that the plasma temperature should be about forty thousand degrees―much higher
![]()
Figure 1. From [2] : Photograph (no external lighting) of a cloud of SL bubbles generated with an ultrasonic horn in 96 wt% H2SO4 saturated with Xe gas; the diameter of the Ti horn tip is 1 cm.
than the temperature of the sun’s surface. Even Hollywood produced a movie in which the central character created a fusion reactor using the SL. The authors of these hypotheses have to claim something similar to the phrase quoted above [1] . Indeed, let us remember the gigantic efforts that scientists are making to create plasma within these parameters―huge complex installations using a magnetic field to keep the plasma from contact with any walls. These installations require hundreds of kilowatts of energy, while the installation for SL consumes a few watts of energy. So what’s the deal? “Equilibrium” is the key word in the phrase given above. This leads to a simple analogy: If we try to apply the laws of Planck’s equilibrium radiation to the solid-state laser or blue LED, we also see that the calculated temperature of the emitting medium would have to be thousands of degrees. The fact is that the CL and SL, similar to the laser and LED radiations, are nonequilibrium ones. We suppose that the CL and SL radiations arise from the phase transition of the first kind. Mechanical waves in fluids create periodic changes of pressure. Under the influence of this force field, bubble size varies. When the bubble size increases, a low pressure arises inside it, and the liquid evaporates from an inner surface of the bubble, taking energy from the surrounding liquid. When the bubble shrinks, the pressure inside it rises, and the vapor condenses. It is at this point that the CL or SL radiation arises, because liberation of the latent energy of vapor condensation occurs. It is the PeTa effect.
A review in detail of hydrodynamic CL and SL is out of the scope of this paper. Readers can find them, for instance, in very informative books [3] [4] . Below we will present only a short review of experimental studies of these phenomena in order to understand their nature.
2. Hydrodynamics Cavitation
At the beginning of the 20th century in England, the Royal Navy had a problem with erosion of the ship’s propeller screws. Lord Rayleigh had begun investigation of this phenomenon, and he found that cavitation was responsible for the erosion [5] . Zones of high and low pressures are formed as a result of turbulent movement of a liquid. With respect to the well-known pressure and temperature dependence of the boiling point, at the zones of low pressure the boiling of the liquid begins (Figure 2) and bubbles are formed. Created by the rotation of the ship’s propeller foam path is clearly visible behind a ship. The resulting bubbles are filled with liquid vapor and gas that naturally had been dissolved in the liquid. The vapor is formed by the evaporation of the liquid from the inner surface of the bubbles. Gases diffuse from the volume of liquid to the inner surface of the bubble and also fill the bubbles. When the bubbles return to the high-pre- ssure zone, their size decreases.
In this process, some part of the steam condenses and again part of the gas is dissolved in the liquid due to back diffusion. The remainder of steam and gases in the bubbles are compressed. As a result, the bubbles collapse with the formation of shock waves, which damaged the ship’s propeller screws and other underwater parts.
![]()
Figure 2. From French Wikipedia: The well-known phase diagram of water near the triple point explaining the liquid-vapor transition during cavitation.
3. Hydrodynamic Cavitational Luminescence (CL)
There are many observations of CL. Several dozen theoretical models try to explain this phenomenon [3] , but thus far, its nature has remained unknown.
The very first observation of light flashes during hydrodynamic cavitation is described by Konstantinov [6] . The flashes were about 0.2 - 0.3 mm long behind the trailing edge of a cavitating cylindrical obstacle. These flashes were bright with a bluish tinge. Other flashes with a diffusive yellowish tinge occasionally appeared around a boundary of the cavitation region. In the above-mentioned book [3] , there are reviews of many similar experiments and observations. For instance, two cases describe when light flashes were recorded in the intensive flows of water from hydroelectrical stations.
More recent examples of observation and practical use of CL are described by Takiura with co-authors [7] [8] . The researchers recorded faint light emission during investigation of cavitations on the mechanical heart valves. A 20-mm Björk-Shiley valve was submerged in the 10 L deionized water tank, and then the pressure difference of 150 mm Hg was exerted on the valve at a rate of 60 bpm with a pulse duplicator. A highly sensitive charge coupled device camera (C2400-35 VIM) was adopted in this study. The camera and the water tank were settled in the lightproof configuration. This camera can observe low light down to the single photon counting range, and it gives two-dimensional mapping of the light. After 2 hours of exposure, faint light images have been obtained successfully. The light emitted mostly from the edge of the occluder on the inflow side in the major orifice of the valve. Therefore, the results suggest that the bubbles would implode around this region.
4. Sonoluminescence (SL)
From the point of view of investigating the phenomenon, SL is the most convenient light emission during cavitation, when the creation of vacuum and compression zones can be monitored in the liquid by ultrasound waves. It was discovered in 1930. Marinesco and Trillat [9] found that a photo plate in water could be fogged by ultrasound. Practically at the same time in the University of Cologne, Frenzel and Schultes put an ultrasound transducer in a tank of photographic film developer fluid. The reseachers hoped to speed up the development process. Instead, they noticed tiny dots on the film after developing and, thus, revealed that the bubbles in the fluid were emitting light with the ultrasound turned on [10] . This phenomenon is now referred to as multibubble sonar- luminescence (MBSL) (Figure 1). The spectra of MBSL were first recorded by Paunoff [11] . Spectrograms were obtained with exposures ranging from 12 to 48 hr. The spectrum was a broad band between 0.446 and 0.658 μm. At the period of the study of CL and SL until now, the main efforts have been focused on explaining these phenomena in terms of emission of high temperature plasma. For instance, in accordance with theoretical papers [12] [13] , during SL implosion of bubbles their contents may be adiabatically heated to temperatures between 5000 - 10,000 K. The cavitation is not only restricted to a finite range of frequencies w and vapor nuclei of sizes R0 but also to a fixed range of hydrostatic pressure PA and alternating pressure amplitude P0. This SL should vary in the same way as the intensity of cavitation and should decrease with w. It should only appear for nuclei of a certain range of R0, show a sharp threshold at low P0 (and low power), and decline above certain critical values of P0 and РA.
With regard to experimental recordings of MBSL spectra, it was shown in some papers [14] [15] that the spectra have an appreciable ultraviolet component. From the 1950s to the 1970s, the paper of Taylor and Jarman [16] seems to be the most interesting and informative one. Using a specially designed scanning spectrophotometer, the authors studied the spectra of MBSL from various aqueous solutions acoustically cavitated at 16 kHz and 500 kHz. Spectra were located in the near ultraviolet, visible, and is likely in the near infrared region of the spectrum. There was a small influence of dissolved gases as well as of the ultrasound frequency on the character of the spectra. The authors did not reject the idea of very high temperatures inside the bubbles but proposed, from our point of view, the most reasonable model of SL at their level of understanding: a part of the light emitted from cavitation is due to an incandescence of the bubble contents and the other part is due to chemi-luminescent reactions within the bubble. Ayad [17] supported a thermal nature of SL as well. In the experiment, 1 W ultrasonic generator of 24 kHz was used and the author has recorded an appreciable infrared component. For measurement, he used a spectrometer with a thermocouple detector and a lead sulphide photometer. The peak of emission with wavelength 1.05 μm was detected. The second peak, with λ = 0.9 μm, that was not mentioned by the author can likely be recorded on this curve. The measured signal, radiated into the angle of 4π steradians from a volume of 6 × 10−5 m3, had a value of (1.6 ± 0.2) × 10−8 W. Barber and Putterman [18] reported that the bubble emits light pulses of picoseconds in duration.
It was too difficult to analyze the effect in early experiments because of the complex environment of a large number of short-lived bubbles. The discovery of single bubble sonar-luminescence (SBSL) [19] [20] eased the problem. In SBSL, a single bubble that is trapped in an acoustic standing wave emits a pulse of light with each compression of the bubble within the standing wave (Figure 3 and Figure 4). This technique allowed a more systematic study of the phenomenon, because it isolated the complex effects into one stable, predictable bubble.
In the above-mentioned paper [1] , the authors used the combined measurements of spectral irradiance, Mie scattering, and flash width (as determined by time-correlated single-photon counting). They point out that the transduction of sound into light through the implosion of a bubble of gas leads to a flash of light whose duration is delineated in picoseconds and suggest that SL from hydrogen and noble-gas bubbles is equivalent to radiation from a blackbody with temperatures ranging from 6000 K (H2) to 20,000 K (He) and a surface of emission whose radius ranges from 0.1 μm (He) to 0.4 μm (Xe). With regard to experimental observations: The fall of SL with ambient temperature the authors explained, since the vapor during the collapse stage would remove energy that will
![]() (a)
(a)![]() (b)
(b)
Figure 3. (a) and (b) Single-bubble sonoluminescence (SBSL): (a) From [22] : Sketch of a typical setup for generating SBSL; (b) From [2] : Photograph of SBSL (center white spot), generated in 85 wt% H2SO4 partially regassed with Xe. The diameter of the spherical quartz cell is 6 cm. The exposure time was 2 s, and the photograph was taken in a fully lit room.
![]()
Figure 4. From [1] . Spectrum of 33 kHz SL from a bubble formed in water (23˚C) into which H2 was dissolved at a partial pressure of 5 torr. Solid curve, fit to a black body at 6230 K. The flash width of 110 ps requires emission from a surface with radius 0.22 μm. Dashed curve, bremsstrahlung fit with a temperature of 15,000 K. Inset, plot of c/TBB function of c, the ionization potential of the gas used to make SL.
Suslick and coauthors [2] [21] conclude that acoustic cavitation, the growth and rapid collapse of bubbles in a liquid irradiated with ultrasound, is a unique source of energy for SL. Spectroscopic analyses of SBSL as well as MBSL have revealed line and band emission, as well as an underlying continuum arising from a plasma (Figure 5). Application of pyrometric and spectrometric methods, as well as tools of plasma diagnostics to relative line intensities, profiles, and peak positions, have allowed the determination of intracavity temperatures and pressures. These studies have shown that extraordinary conditions (temperatures up to 20,000 K; pressures of several thousand bar; and heating and cooling rates of >1012 Ks−1 are generated within an otherwise cold liquid. Regarding the appearance of peaks in the near-IR region (Figure 5(b)), the authors explained the intra-atomic electron transitions within the rare-gas atoms inside the bubble as follows: The emission lines in the near infrared arise from excited state to excited state transitions within the Ar 4p − 4s manifold. The energies of the 4p levels range 12.9 to 13.4 eV, whereas the energies of the 4s levels range 11.5 to 11.8 eV.
![]() (a)
(a)![]() (b)
(b)
Figure 5. (a) and (b) From [2] : (a) SBSL spectra from degassed water partially regassed with Ar or Xe compared to 85 wt% H2SO4; (b) Single-bubble sonoluminescence as a function of Pa for 85 wt% H2SO4 partially regassed with Ar.
Brenner with co-authors [22] discussed the following interesting results: A comparison of time dependence of bubble’s radius R(t), driving pressure P(t), and light intensity I(t), as measured in [20] ―(Figure 6 from [19] ). A negative driving pressure causes the bubble to expand; when the driving pressure changes sign, the bubble collapses, resulting in a short pulse of light marked SL.
It is interesting to mention that the spectrum of SBSL for water at 22˚C [23] (Figure 7(a)) practically repeats the spectra recording more than twenty years before [16] . According to the authors, these experimental spectra can be compared with the blackbody radiation for appropriate temperature. Hiller with co- authors [23] suggested using the blackbody temperature 25,000 K for their emission. At the same time, Brenner with co-authors [22] believe that the temperature 40,000 K better corresponds to the experimental data (solid line in Figure 7(a)).
Matula with co-authors [24] compared (Figure 7(b)) MBSL (thin line) and SBSL (thick line) spectra in a 0.1 M sodium chloride solution. Each spectrum was normalized to its highest intensity. Let us note existance (MBSL) and absence (SBSL) of the sodium band near 589 nm. The first measurement of SBSL pulse widths is very impressive [25] (Figure 8). The parameters were Pa = 51.2 bars, f = 520 kHz, and the gas concentration was 1.8 mg/L O2. Both the width in the red and the ultraviolet spectral range were measured. According to the authors, the indistinguishable widths rule out blackbody radiation, but not a thermal emission process in general.
Ketterling and Apfel [26] presented (Figure 9) an experimental phase diagram for air saturated in water to 20%. Each data point represents the Pa and R0 found from a single R(t) curve and is indicated to be luminescing and/or stable. The
![]()
Figure 6. From [22] : Radius R(t), driving pressure P(t), and light intensity I(t) from [19] , as measured in [20] ; 0, 1, 2, 3, 4 are points used in our model.
![]() (a)
(a)![]() (b)
(b)
Figure 7. (a) and (b) SL spectra: (a) From [23] : Spectrum of SBSL for water at 22˚C. Solid line-a blackbody spectrum at 40,000 K suggested in [22] ; (b) From [24] : MBSL (thin line) and SBSL (thick line) spectra in a 0.1 M sodium chloride solution. Each spectrum was normalized to its highest intensity. Note the prominence (MBSL) and absence (SBSL) of the sodium line near 589 nm.
![]()
Figure 8. From [25] : First measurement of SBSL pulse widths.
![]()
Figure 9. From [26] : Experimental phase diagram for air saturated in water to 20%.
curves in the plot are lines of diffusive equilibrium for a given gas concentration c∞/c0 = 0.2 (solid line) and c∞/c0 = 0.002 (dashed line). The range of Pa where dancing bubbles were observed is indicated, as are regions of bubble growth (g) and dissolution (d) relative to each equilibrium curve. The stable no-SL points (d) correspond to a stable chemical equilibrium, which would lie above the c∞/c0 = 0.2 curve if plotted.
Brennan and Fralick [27] suggested a cold model of the SL. The authors measured the timing of SL by observing laser light scattered from an SBSL. They performed this measurement on 23.5 kHz, 17.8 kHz, 13.28 kHz, and 7.92 kHz systems and found that the flash typically occurs 100 nanoseconds before the minimum radius. These results motivate a new model of SL: the flash occurs from the discharge of an excited cold condensate formed during the adiabatic expansion of the bubble. At that moment, the bubble wall motion is subsonic, and thermodynamic models imply that internal temperatures and pressures are crossing thru moderate conditions. Thus, the “hammer striking the anvil to create a spark” model of SL may be invalid. Instead, the authors note that the same adiabatic models that are successful in modeling bubble motion imply that very cold temperatures can exist in the bubble: During the expansion cycle, the bubble starts near room temperature at its equilibrium radius. At the top of the expansion that follows, the adiabatic model implies that temperatures as low as 4 K are reached. This is cold enough to condense most gases and any water vapor present in the bubble. Conservation of energy arguments imply that this meta- stable condensate should contain several MeV of energy. This excitation energy comes from the latent heat contained in the gases just before they condensed. As the bubble shrinks and passes through its equilibrium radius, the condensate will be destroyed and discharge its energy. This model predicts that each condensate stores an amount of latent heat energy E released in the discharge given by the following:
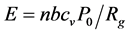 (1)
(1)
where n is the number of moles of gas in the bubble, b is the Van Der Waals excluded volume per mole, cv is the constant volume heat capacity per mole of the gas in the bubble, P0 is the ambient atmospheric pressure, and Rg is the ideal gas constant. For bubble sizes around 8 to 10 μm, this formula predicts that each flash will release about 1 pico Joule (7 MeV) of energy. Calibrated measurements of bubble brightness show that each flash contains about this much energy. Furthermore, this formula predicts that bubbles containing xenon will be brighter than krypton or argon, because of xenon’s larger Van Der Waals excluded volume, an effect that is also observed. High temperatures are achieved once the discharge takes place, but are not seen as the cause of the flash in this model.
5. Short History of the PeTa Effect Discovery
“Everybody knows that it is impossible. But somebody arrives, who does not know that it is impossible, and he does it.”
―A. Einstein
Now let us discuss the PeTa effect, which in our opinion is the basis of CL and SL. Between the years 1979 and 1984, in the former Soviet Union, three papers were published that presented rather unusual experimental data: The appearance of characteristic infrared radiation accompanying crystallization from the melt of some infrared transparent substances (seven alkali halides, led chloride, and sapphire) [28] [29] [30] . These results were not casually obtained. They were preceded by a long search for the characteristic radiation of crystallization on the basis of a new approach to the latent energy liberation suggested by the author of this paper in 1964. Allow us to remind you that in 1964 the Soviet physicists N. G. Basov and A. M. Prokhorov and the American physicist Ch. H. Townes were awarded the Nobel Prize for their invention of lasers. At that time, the author of this paper, a researcher of 25 years old, was working at the Leningrad Physical and Technical Institute after A.F. Ioffe of the USSR Academy of Sciences, investigating the crystallization from melts. Certainly, I was very impressed with the discovery of the laser effect, and it was natural to find an analogy between laser mediums and my crystallizing systems (Figure 10).
It is well known that crystallization from the melt or condensation or deposition from vapor phase can be described as transitions of particles from an excited meta-stable energy level in the super-cooled melt or supersaturated vapor to the lower stable ones correspondingly in the solid or liquid. The gap between these two levels corresponds to the latent energy of crystallization per atom or molecule. It is very similar to Figure 10, but the only difference is that we do not need to use an external source of energy for pumping. The particles on the excited ievel appear as a result of super-cooling of melts or super-saturation of vapors before phase transition.
In the widespread description of the crystallization process, for instance from melts, it is postulated that each act of particle transition from the melt to the solid produces several phonons. This process contributes to Planck’s radiation
![]()
Figure 10. Analogy between a laser and the PeTa radiations.
by the particle’s increased motion, and hence, temperature. A gradient of the temperature is needed to remove this additional heat, and thus, to continue crystallization. It means that the latent energy of the first-order phase transitions can be removed only by thermo-conductivity.
But I suggested that the act of transition can produce one or more photons (similarly Figure 10). The energy of the photon has to be equal to the full latent energy of crystallization per one particle, if one photon is produced, or to part of this energy, if more than one photon is produced. A photon of suitable energy from Planck’s radiation could play a role of a trigger of emission. The emitted energy could be a little higher for some particles if they, in addition, are activated or the lower level is lowered with respect to the main level by super-cooling or some other effects.
The estimations showed that during crystallization in the simplest case― emission of one photon for one transmitted particle (atom or molecule) radiation has to take place in the infrared. This is the reason why, for first experiments, I decided to choose crystallization of substances that are transparent in the infrared. Before, I had worked with alkali halides crystals―it was my thesis for the master’s degree [31] . All alkali halides are transparent in the infrared, and I decided first to search the characteristic radiation during their crystallization.
In 1966, on the basis of my assumptions, I began experiments at the Leningrad Physical and Technical Institute after A.F. Ioffe of the USSR Academy of Sciences. The experiments were continued at the Solid State Physics Institute of the USSR Academy of Sciences from 1973-1983 with few interruptions, and at MIT (the United States) in 1978 during my science trip there. There were several reasons why it was very difficult for me to complete this program. Two of these reasons were administrative ones. First of all, during all of my scientific activity I had been working in laboratories of crystal growth, and I had to complete the crystal growth programs, especially the development of industrial crystal growth technologies. Secondly, the optical measurements were out of the scope of these laboratories. We did not have any optical equipment, and I needed to look for it outside the labs. The third reason was an experimental one. For the experimental substances, the characteristic radiation is at the range of maximal Planck’s radiation corresponding temperatures of melting, and it was very difficult to separate the characteristic radiation from the Planck’s radiation. Thus, the first positive results were obtained in 1970. I have chosen the title “Infrared Characteristic Radiation (IRCR) under first-order phase transitions” for this effect. The results were unusual from the point of view of all specialists in the field of optics. They rejected a high-temperature luminescence possibility in favor of the phonon path of energy removal. I had to look for more and more experimental and theoretical evidence that the crystallization was the source of the radiation.
At the same period of time, M. Perel’man, a theoretician from the Institute of Cybernetics in Tbilisi (former Soviet Union), published a series of theoretical papers in which he predicted the same effect [32] [33] [34] . I never met him, but in 2006, we established contact through the Internet, combined our efforts, and published three mutual papers [35] [36] [37] . M. Perel’man died in 2010. In memory of Prof. M. Perel’man, and to simplify the title “IRCR under first-order phase transitions,” the term “PeTa (Perel’man-Tatartchenko) effect” is used in this paper, as it was proposed during a discussion of the problem in the journal New Scientists [38] .
As it was mentioned above, the basis of the PeTa effect is that an excited particle (i.e., atom, molecule, or/and cluster) emits transient radiation during the transition from a meta-stable higher energy level (in a super-cooled melt or a super-saturated vapor) to a stable lower level (in more condensed phase―a crystal or a melt). The radiation removes the latent heat by photons with characteristics for the substance frequencies that are generated under this transition.
Evidence of the PeTa effect does not follow from existing phase-transition conceptions. Our opponents doubt the existence of high-temperature luminescence and insist on the removal of the energy of the phase transition by means of thermo-conductivity, i.e., by phonons. Here is an example of their reasoning for a case of semiconductor melt crystallization [39] : Let us consider an excited particle near a phase-transition boundary. For phase-transition radiation to occur, the probability of excitation energy being converted into light emission by this particle at phase transition has to be equal to or greater than the probability of the excitation energy being converted to heat. But this probability is negligibly small: for a free molecule in the excited state, its optical lifetime (the longitudinal relaxation time) t1 is equal to 10−7 - 10−8 s. For transitions in the near-infrared range at the temperature T ≈ 1000 K, the nonradiative multiphonon relaxation time in solids t2 is equal to or less than 10−9 s [40] . Then, the probability of light emission ξ ~ t2/t1 - 10−2 << 1 and a nonradiative phase transition has to be realized. As it follows from Einstein’s statement quoted above, if I were more educated in the field of optics, these arguments were sufficient for not looking for a characteristic radiation. But I received the positive experimental results before to know these arguments. Now in addition to the experimental results, I found a theoretical objection to the opponents: We know cases when ξ > 1, and thus, radiative phase transitions have to be possible. Indeed, phase transitions of the first order are collective phenomena with participation of a big ensemble of excited particles, while previous consideration of our opponents was made for a separate particle. For an ensemble of particles in our conditions, the super-radiation Dicke’s effect is applicable [41] . The phenomenon of super-radiation is that a system of excited particles undergoes optical transition to a lower level due to their interaction with each other through the common radiation field, the transition time t1 being much shorter than the radiative decay time of an individual particle. For an ensemble of numerous particles, t1 is a value inversely proportional to N―the number of particles participating in the phase transition. For the number of particles N = 105, t1 is equal to 10−12 s, which is much less than t2 = 10−9 s. Thus, if
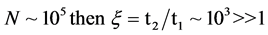 (2)
(2)
and the radiative phase transitions will be realized. Now, a theory of the super- radiation is well developed, and there are several lines of experimental evidence of it, but not to first-order phase transitions [42] [43] .
Here is the other interesting point of view concerning our conception. In 1972, the famous Soviet physicist academician, Nobel Peace Prize winner A.D. Sakharov, supported the effect under consideration and presented two theoretical Perelman’s papers for publishing in the USSR Academy of Sciences Sov. Phys. Dokl. [33] [34] . Here are M. Perel’man’s memories about these events (translated by us from Russian):
“In 1970 I told Sakharov of my theory, according to which during the phase transition (for example, in the condensation of vapor or freezing of water) the released heat is converted to infrared characteristic radiation. This idea seemed from the first glance so wild that I have lost a hope to at least tell somebody it to the end. A. Sakharov had carefully listened to all and, of course, began as patiently to explain to me that it can’t be, but I never gave up, brought all the new arguments. It was lasting two nights. Suddenly the Sakharov once said, as if reprises aloud: ‘Listen, it’s very easy! If, for example, super-cooled liquid freezes quickly, the release of heat is a volumetric process but rate of any heat transfer, except to radiative one, is proportional to the surface area. So they are incompatible. Urgently, sit down and write a paper!’ … The necessity of the effect he apparently had no doubt. Moreover, he insisted that I carry out the experiments, saying that otherwise he himself will hold them in his kitchen… The method of reasoning by A. Sakharov, he acknowledged the possibility of the existence of the effect of the radiation was the easiest of all possible-he compared the dimensions of two processes: heat generation and its removal. It is only necessary to emphasize that these arguments are not only the simplest ones they are, at the same time, the most fundamental. (Apparently, it is because of the creations of genius it seems that when they are understood and accepted, they are always very simple) [44] .
The author of this paper did not have any support like M. Perel’man. For instance, at the beginning of 1974 at the session of the Scientific Council of the Solid State Physics Institute of the USSR Academy of Sciences, I had presented experimental results for publishing. There were many opponents. The main one was Prof. V. L. Broude, a member of the team that discovered the exiton. For my experimental results, their opinion was that I needed to look for mistakes in them. With regard to the Perel’man’s theory, they said that it was not evident. Thus, the paper was rejected. Only in 1977, when I had found sufficient arguments (especially Dicke’s super-radiation [42] ), was the paper accepted for publication [28] .
If we accept our conception of the nature of the PeTa effect, the main formulas for ranges of radiation follow [35] [36] : (3)-(5).
5.1. For One-Photon Radiation, We Have
 (3)
(3)
Here the latent energy of phase transition L is expressed in kJ/mole, and the wavelength λ1 of emitted radiation in µm, NA is the Avogadro number.
5.2. The n-Photon Emission with Equal Frequencies νn Has a Wavelength λn
 (4)
(4)
5.3. Dimers and More Complicated Formations (Clusters)
Can be represented as single particles, and if the bound energies of atoms/mo- lecules in them are small enough, wavelengths of radiation for a cluster from M
atoms/molecules for n photon emission  will be of the type:
will be of the type:
![]() (5)
(5)
We repeat that for all substances previously studied experimentally, PeTa radiation is located in the infrared range. This is the reason of the first title of the effect―IRCR (infrared characteristic radiation). However, we now know that on some conditions, for instance, at a high pressure in the gas phase, formation of clusters on a preliminary stage of the phase transition is possible. In this case, in the Formula (5) M > 1, and thus λ can be located in a visible or even in the ultraviolet range. Thus, PeTa effect is a characteristic radiation (CR) under first order phase transitions.
Besides CL and SL, there are a lot of manifestations of PeTa effect in nature. Consider just two of them.
5.4. PeTa Radiation under Cloud Formation
Almost 50 years ago, several pictures Figure 11(a) and Figure 11(b) were published [58] in which infrared radiation is clearly seen in the formation of clouds. The authors honestly admit that the nature of this radiation is unknown to them.
![]() (a)
(a)![]() (b)
(b)
Figure 11. (a) and (b) similar to [58] : Example of manifestations of PeTa effect in nature: Photographs of forming cumulus cloud in different wavelength ranges: (a) visible range; (b) infrared 8 - 14 µm range.
But it was 50 years ago. We now know that this is the PeTa effect. So why do scientists continue to ignore the PeTa effect existence in all works related to the earth’s atmosphere? How can we get adequate models of weather and climate if the radiation effect in the formation of clouds and fog is not considered?
5.5. Gigant Planets Color
Why do the giant planets, especially Jupiter, have such a bizarre patchy color (Figure 12)? What is the nature of the Juvenal red spots? The Big Juvenal Red
Spot has already been known for 400 years. This is a giant whirlwind that is larger than the size of the Earth, and the wind speed there reaches thousands of km per hour. Hundreds of scientists are searching for the mythical coloring substances in the atmosphere of Jupiter. But this is a totally absurd idea. Firstly, if these substances exist, the concentration of them does not exceed 1:106. Secondly, during a permanent whirlwind raging in an atmosphere, it should all mix and make a uniform color. On the other hand, we propose a very clear explanation of these phenomena: The intensive circulation in the atmosphere of Jupiter lifts heated vapors, particularly of ammonium and water, which are condensed, solidified, and deposited in the upper cool layers of the atmosphere. (Satellites found clouds of crystals of these substances in the Juvenal atmosphere). The PeTa emission occurs during these condensation, crystallization, and deposition. Color and power of the PeTa radiation are determined by pressure, temperature, intensity of mixing, and the position of the emitting layer. It means that nature gives us information on the physical processes in the planet’s atmosphere through the colors and power of this radiation. Why don’t we perceive this? Of course, we need to study the language of nature. For this purpose, laboratory experiments must be carried out to find the color and intensity of PeTa radiation at the actual conditions of condensation, freezing, and deposition of gases in the Juvenal atmosphere. We have already begun this research. Readers can find impressive experiments on the PeTa radiation under condensation and deposition of air components in the papers previously published in this journal [56] [57] .
6. Discussion of the CL and SL Mechanisms on the Basis of the PeTa Effect
“After all, if the cloud collapses violently enough to break the molecular bonds in a solid, causing cavitation damage, there is no reason why photons should not also be emitted.” [22] .
Now let us return to the discussion of CL and SL problems. Below we will show that our model, which is the opposite of the above quote from the paper [22] , explains all the experimental data mentioned in the above review. At the same time, it is very important to note that it is based on real physical processes, and there is no scientific fiction similar to the existence of plasma inside the bubbles. We decided to apply our model for a particular experiment. The following are the main points of the application of the model to the experiment (Figure 6).
1) We introduce the following notations:
PA is the atmospheric pressure, PL is the hydrodinamic pressure of the liquid, PD is the alternative driving pressure, PDm is the amplitude of ultrasonic wave, P0 is the Laplace pressure inside of the bubble, PV is the pressure of vapor of the liquid inside the bubble, and Pg is the pressure of a gas inside the bubble.
At any time, instantaneous equilibrium of forces acting on the bubble wall should be performed:
![]() (6)
(6)
2) Let us begin from a middle point of time t1 = 300 μs, which we denote the number 1 (Figure 6).
The bubble size at this point is minimal R01 ≈ 20 μm. Equation (6) for the bubble point 1 is: PA + PL + PD1 + P01 = PV1 + Pg1. Let us calculate all these pressures: PA ≈ 101 kPa. A depth of the bubble location is ~0.1 m, which means that PL ≈ 1 kPa. With respect to experimental conditions, PDm ≈ 1.2 PA. At this point PD1 ≈ PDmax ≈ 121 kPa. We assume that the temperature inside the bubble is equal to 68.5˚C. Why this temperature is selected? The fact that the temperature 68.5˚C immediately allows us to obtain a closed solution that satisfies the boundary conditions given by experiment. That is why we chose it as the first iteration. It means that the water surface tension γ ≈ 65 × 10−3 Nm−1. P01 = 2γ/R01 ≈ 7 kPa. Thus, Equation (6) is transformed into
![]() (7)
(7)
3) Let’s carry out a similar analysis of the bubble wall equilibrium at point 2 (Figure 6).
It corresponds to the time t2 = 470 μs. Here the bubble has a maximal size R02 ≈ 80 μm.
For the mechanical equilibrim of the bubble wall, Equation (6) has to be fulfilled at this point: PA + PL + PD2 + P02 = PV2 + Pg2. Let us calculate all these pressures. PA and PL are the same as at point 1: PA ≈ 101 kPa, PL ≈ 1 kPa. At this point PD2 ≈ −0.6PDmax ≈ −72 kPa. We suppose the same temperature 68.5˚C at this point (isothermal model as in Figure 2). P02 = 2γ/R02 ≈ 2 kPa.
Thus, Equation (6) is transformed into
![]() (8)
(8)
4) Now we estimate the thermodynamic state of the water vapor and air inside the bubble:
The mass of vapor in the bubble at any stage of its development can be determined according to the formula of Hertz-Knudsen:
![]() (9)
(9)
where: G is the mass of steam evaporating or condensing per unit time per unit surface; α is the accommodation coefficient; Pv is the vapor pressure above the surface at which evaporation or condensation occurs; M is the molecular weight of the vapor; B is the universal gas constant; and T is the absolute temperature.
The curvature of the surface, which evaporates the vapor is not included in the consideration. Knowing the mass of steam that evaporates from the unit surface per unit time, we can determine the time τ, during which the vapor of density ρv can fill a cavity of radius R due to evaporation processes.
![]() (10)
(10)
If ρv is the vapor density at saturation pressure, by using the equation of the state of the vapour
![]() (11)
(11)
Equation (10) can be transformed:
![]() (12)
(12)
It follows that during the expansion of the cavity, vapor pressure therein is equal to the saturation pressure only when the expansion of the cavities and maximum radius achieved in the expansion phase are related by
![]() (13)
(13)
where τexp is the time of expansion of the cavity and Rmax is the maximum radius achieved by bubbles in the expansion stage.
The value of the accommodation coefficient for water is within the range α = 0.04 ... 1.0. For greater reliability of our estimates we use a small value of the accommodation coefficient α = 0.2. Thus, it follows from (13) that for the water at ~70˚C inside the cavitation bubble, vapor will always have the saturation pressure if its expansion is realized with condition:
![]() (14)
(14)
For our case Rmax ≈ 80 μm, τexp ≈ 170 μs, and we obtain Rmax/τexp ≈ 0.5 m/s. Thus, condition (14) is fullfiled. In different experiments, CL and SL were observed in the frequency range 1 Hz to 2 MHz. For f = 1 Hz situation is evident. For f = 2 MHz, Rmax/τexp ≈ 40 m/s. This is higher than the value from (14). It follows that at the highest frequencies at expansion of the bubble, equilibrium vapor pressure is not attained. However, this does not significantly affect our model, but the parameters of the calculations will be a little more compli- cated.
5) The mass of gas in the cavitation bubble can be determined by Henry’s formula:
![]() (15)
(15)
Here Mg is the mass of the gas in the cavitation bubble; C (R0) is the initial concentration of gas in the liquid layers adjacent to the wall of the cavity; K is the constant of Henry; and R0 is the initial radius of the cavitational bubble. The mass of gas in the cavitational bubble may be accepted the same when considering a single cycle of its expansion and contraction, since the change in mass due to gas diffusion is insignificant.
6) Let us continue the analysis of the situation at point 2 (Figure 6):
Here equality (8) should be performed: PV2 + Pg2 ≈ 32 kPa. The equilibrium vapor pressure at 68.5˚C: PV2 = 28.86 kPa. Hence, the gas pressure at this point: Pg2 = 3.14 kPa.
7) Return to point 1, where equality (7) should be performed:
PV1 + Pg1 ≈ 230 kPa. Above we accepted that the mass of the gas inside the bubble has not changed. Let us assume that the gas obeys the equation of state for ideal gases. The volume of the bubble at point 1 is 64 times smaller than at point 2. Consequently, the gas pressure should be 64 times higher: Pg1 = 64Pg2 = 201 kPa. For the constant temperature: PV1 = PV2 = 29 kPa. Hence, the vapor pressure has not changed. But the mass of vapor in bubble 1 M1 is much less than in bubble 2 M2, simply because of its smaller size.
8) We calculate both the mass M2 and M1:
For vapor density at this temperature ρv = 51 g∙m−3. We obtain M2 = 109.3 × 10−12 g, M1 = 1.7 × 10−12 g. A mass deficit is ΔM = M2 − M1 = 107.6 × 10−12 g ≈ 1 × 10−10 g. Consider a point 0 equivalent to 2, corresponding to the time t0 ≈ 270 μs (Figure 6). Evidently M0 = M2. So, where has this vapor disappeared to on the way from point 0 to point 1?
9) Let us follow the process between points 1 and 2:
The initial bubble is ~20 μm in size. The vapor of liquid and gases dissolved in the liquid are at the equilibrium pressure inside the bubble. Pressure of ultrasonic wave starts to decrease. The gas pressure inside the bubble becomes uncompensated, and bubble radius begins to increase. This leads to the fact that the vapor pressure becomes below the equilibrium, and the liquid evaporates from the inner surface of the bubble. Energy for this process is taken from the liquid, and thus, the temperature of liquid around the bubble decreases a little. But we consider this process as isothermal, since a small drop in temperature is not essential to our model. When the size of the bubble has reached its maximum value, from the inner surface thereof a large amount of liquid had evaporated and thus the vapor pressure inside the bubble is again equal to the equilibrium pressure. Thus we came to point 2, the situation in which we had in detail analyzed before.
10) Now the phase of the sound wave compression comes, and the bubble size is reduced:
We are going to point 3, which corresponds to the time t4 ≈ 480 μs. It is more or less equivalent to point 1. We can see that this process is much faster than expansion: Reducing the bubble radius from 80 to 30 μm is achieved in 10 μs. Nequality (15) is not satisfied, and the vapor pressure remains above the equilibrium. Part of the vapor molecules near the surface of the bubble condense, but the majority remains in the volume of the bubble due to the absence of condensation nuclei. The liquid vapor becomes supersaturated. At this time, at an elevated pressure, the two processes are carried out: First, for the vapour molecules are energetically favored to form clusters, and this occurs with a high probability. Second, the vapour molecules and clusters are in an excited state with respect to the bulk liquid molecules, and in conformity with [41] , there is an interaction of molecules and clusters through the collective radiation field. We obtain the classic version of the situation in which PeTa radiation has to be implemented. As we have shown above, the energy accumulated in the vapor, during tens of picoseconds, has to be emitted. It is at this point we see the SL flash (Figure 6). During the next ten nanoseconds, condensation of vapour is realized, and the bubble collapses, forming a shock wave in the liquid.
11) After that, in accordance with the discussed above conditions of equilibrium bubble, it starts to expand. Subsequent alteration of the bubble size is probably due to the arrival of a reflected shock wave.
12) Of course, our isothermal description of the process, as in Figure 2, is only the first iteration.
Indeed, in reality, the temperature inside the bubble is changed. In addition, during increasing of the bubble, liquid temperature in the vicinity of the bubble should decrease because the liquid evaporates, and this decreasing of the temperature is a source of the CL and SL energy. We need a more time for other precise iteration. But it requires only solving of common thermophysical and electrodynamic problems with reasonable boundary conditions. Preliminary estimations show that the temperature before and during the flash are is not comparable with 40,000 K or even 4 K in other models. Changes of pressure are an order of sound wave amplitude, i.e., several hundred kPa. Thus, this is not a science fiction! No plasma! No Hollywood!
13) During the collapse:
Because of instantaneous condensation of vapor after the flash, a speed of the bubble wall may be supersonic, which can cause considerable dynamical pressure. But this energy goes at the formation of a shock wave in the liquid. Thus, there is no reason for the huge increase in temperature, because the energy of the water vapor had already been emitted.
14) Now we calculate the energy of a single pulse and power of SBSL:
![]() In the beginning, we assume that all the energy of the vapor is rejected. Thus, we define the upper limit of the radiation pulse Ep. For the latent energy of evaporation at 69˚C ~ 43 kJ・mole−1, we obtain Ep1 ≈ 25 × 10−8 J. For frequency 24,000 Hz, the maximal power of SBSL is WSL ~ 6 × 10−3 W. Of course, our estimates are very approximate, and the figures give us only the order of magnitude. There are several reasons why this power will be much less. First, some of the vapor molecules settle on the inner surface of the bubble in the compression process; therefore, the real mass of the vapor involved in the emission process will be less. Second, a significant portion of the vapor molecules clustered beforehand, thus reducing the energy of supersaturated vapor. Third, the part of the radiation is absorbed by water and the vessel walls. Thus, it is interesting to estimate the lower power limit. We define it as follows. From Equation (2) the minimal number of molecules for the PeTa radiation pulse is equal to ~105. If we consider the formation of clusters, this number should be ~107. We calculate the energy emitted during condensation of these particles: Ep2 ≈ 10−12 J. The real figure should be between these two values, i.e., Ep ≈ 10−10 J. It follows that the radiation power of the SBSL in the frequency range of 1 kHz to 1 HHz in the range: WSBSL ≈ (10−7 - 10−4) W. But a certain amount of energy will be absorbed by the liquid and the vessel walls.
In the beginning, we assume that all the energy of the vapor is rejected. Thus, we define the upper limit of the radiation pulse Ep. For the latent energy of evaporation at 69˚C ~ 43 kJ・mole−1, we obtain Ep1 ≈ 25 × 10−8 J. For frequency 24,000 Hz, the maximal power of SBSL is WSL ~ 6 × 10−3 W. Of course, our estimates are very approximate, and the figures give us only the order of magnitude. There are several reasons why this power will be much less. First, some of the vapor molecules settle on the inner surface of the bubble in the compression process; therefore, the real mass of the vapor involved in the emission process will be less. Second, a significant portion of the vapor molecules clustered beforehand, thus reducing the energy of supersaturated vapor. Third, the part of the radiation is absorbed by water and the vessel walls. Thus, it is interesting to estimate the lower power limit. We define it as follows. From Equation (2) the minimal number of molecules for the PeTa radiation pulse is equal to ~105. If we consider the formation of clusters, this number should be ~107. We calculate the energy emitted during condensation of these particles: Ep2 ≈ 10−12 J. The real figure should be between these two values, i.e., Ep ≈ 10−10 J. It follows that the radiation power of the SBSL in the frequency range of 1 kHz to 1 HHz in the range: WSBSL ≈ (10−7 - 10−4) W. But a certain amount of energy will be absorbed by the liquid and the vessel walls.
15) With respect to spectra of MBSL and SBSL measurements, all of them are broad bands between the ultraviolet ~0.2 μm, visible and near infrared ~1 μm.
In the PeTa model it corresponds to condensation of different clusters from M moleculs with respect to the Formula (5): ![]() = 43 kJ/mole; MIR = 1,
= 43 kJ/mole; MIR = 1, ![]() = 120/43 = 2.8 μm-IR boundary; MUV = 12;
= 120/43 = 2.8 μm-IR boundary; MUV = 12; ![]() ≈ 0.2 μm-UV boundary. Thus for water Mmax ≈ 12.
≈ 0.2 μm-UV boundary. Thus for water Mmax ≈ 12.
16) In our model, the main role is given to the liquid, in which the cavitation occurs.
The model explains well the main spectra of cavitation. Apparently, the dissolved gases and other impurities in the liquid are responsible for bands that appear at the background of the main spectrum. These gases and impurities can be excited by the shock wave that occurred during cavitation. Indeed, the energy of the waves is massive such that it destroys the underwater parts of ships and is used for artificial crushing of materials. A good illustration of this assumption can be Figure 7(b), which shows spectra of MBSL and SBSL in a 0.1 M sodium chloride solution. The sodium band near 589 nm is recorded only in MBSL. Absence of this line in SBSL proves its excitation in the solution (outside of the bubble) apparently by the shock waves.
Table 1 presents the main experimental parameters of CL and SL and our estimations of them on the basis of the PeTa model.
![]()
Table 1. The main experimental parameters of CL and SL and estimations of them on the basis of the PeTa model.
7. Conclusions
In this paper, on the basis of the PeTa effect, models of cavitational luminescence (CL) and sono luminescence (SL) are developed. In the models, the main role is given to the liquid, in which the cavitation occurs. The evaporation and subsequent condensation of the liquid inside the bubble are responsible for the CL and SL. Apparently, the dissolved gases and other impurities in the liquid are responsible for peaks that appear at the background of the main spectrum. They most likely are excited by a shock wave that occurred during cavitation. This model requires more precise future analysis, but already in this version, the main experimental results have found qualitative explanation.
What is the main value of this model? We have already mentioned above that color and power of the PeTa radiation are determined by type of vapour, pressure, temperature, intensity of mixing, and the position of the emitting layer. Thus, the nature gives us information on the physical processes in a system through the colors and power of the radiation. Of course, we need to study the language of the nature. For this purpose, laboratory experiments must be carried out to find the color and intensity of PeTa radiation at the actual conditions of condensation, freezing, and deposition of vapors and/or gases in the system. To check the PeTa model of CL and SL, we propose the following experiment (Figure 13).
Inside of a polished barrel from sapphire (1) with the test liquid (2) a polished metal or sapphire piston (4) is placed at a certain distance above the liquid surface. The barrel (1) may be fabricated from a bulk sapphire single crystal, or of a profiled sapphire crystal [59] (Figure 14). The liquid (2) is saturated with the gas
![]()
Figure 13. Sketch of a setup for checking of the proposed by the author of this paper PeTa model for CL and SL.
![]()
Figure 14. From [59] Monocrystalline sapphire profiles grown with TPS (technique of pulling from shaper) or VST (variable shaping technique) by the author of this paper with collaborators in the Solid State Physics Institute of Academy of Sciences of Russia.
to the desired pressure through the hole (5). After that, the hole (5) is sealed with a bung (6). The device is ready for use. With the rod (7), the piston can move up and down at a controlled rate and a desired force. The sapphire barrel can withstand high pressure, and it is transparent in a broad range of wavelengths―from ultraviolet to infrared [59] . If scale factors will be taken in account, the experiment allows observing arisen CL, which occur inside the liquid and above of its surface (3) as it follows from the PeTa model. This macroscopic experiment will let to study many parameters of the process.