1. Introduction
Fourier transform (FT) 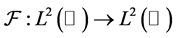 by
by
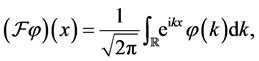
which is a unitary operator, is a fundamental method in function analysis and is applied to many fields in physics. The corresponding self-adjoint operator is given by the harmonic oscillator Hamiltonian 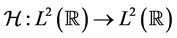 by
by
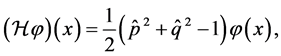 (1)
(1)
where  and
and![]() , through the relation
, through the relation
![]() (2)
(2)
The validity of (2) is verified by noticing that the Hermite polynomial ![]() (multipled by
(multipled by![]() ) is a simultaneous eigenfunction of
) is a simultaneous eigenfunction of ![]() and
and![]() , with their eigen- values given by
, with their eigen- values given by ![]() and
and![]() , respectively.
, respectively.
If a function ![]() is integrable, its FT is well defined. However, if the function
is integrable, its FT is well defined. However, if the function ![]() is not integrable, for example
is not integrable, for example![]() , its FT should be regarded as a generalized function. To calculate the FT of
, its FT should be regarded as a generalized function. To calculate the FT of ![]() in a numerically friendly way, one of the methods is to replace
in a numerically friendly way, one of the methods is to replace ![]() by
by ![]() such that
such that![]() , and to choose
, and to choose ![]() as the resolvent for
as the resolvent for![]() , that is [1]
, that is [1]
![]()
Considering that ![]() includes the term proportional to
includes the term proportional to![]() , we find that
, we find that ![]() behaves like
behaves like ![]() for
for![]() . Thus
. Thus ![]() can be Fourier transformed.
can be Fourier transformed.
To make ![]() square integrable, it is sufficient to reduce the order of
square integrable, it is sufficient to reduce the order of ![]() (for
(for![]() ) by one, not necessarily by two. This implies that it is sufficient to choose
) by one, not necessarily by two. This implies that it is sufficient to choose![]() , not necessarily
, not necessarily![]() , as given above. However, the square root of the operator
, as given above. However, the square root of the operator![]() , in general, is somewhat complicated to deal with, so we adopt an alter- native approach, supersymmetrization. The supersymmetry (SUSY) can be realized by adding
, in general, is somewhat complicated to deal with, so we adopt an alter- native approach, supersymmetrization. The supersymmetry (SUSY) can be realized by adding ![]() in (1) to
in (1) to ![]() [2] , where
[2] , where![]() , representing the fermionic creation and annihilation operators, respectively, satisfying
, representing the fermionic creation and annihilation operators, respectively, satisfying![]() ,
, ![]() , and
, and![]() , with
, with![]() . The modified Hamiltonian
. The modified Hamiltonian ![]() can be decomposed into
can be decomposed into![]() , where
, where ![]() is called a supercharge. Under the modifica- tion
is called a supercharge. Under the modifica- tion![]() , it is natural to transform
, it is natural to transform ![]() to
to![]() , as is analogous to (2).
, as is analogous to (2).
The aim of this paper is replace ![]() by
by
![]()
with ![]() chosen in an appropriate way, to finally find that the introduction of SUSY clarifies the availability of the even-odd decomposition of
chosen in an appropriate way, to finally find that the introduction of SUSY clarifies the availability of the even-odd decomposition of ![]() in a more natural way. In Section 2, we generalize the resolvent kernel for
in a more natural way. In Section 2, we generalize the resolvent kernel for![]() , where
, where ![]() can be regarded as the specialization of the Hamiltonian
can be regarded as the specialization of the Hamiltonian ![]() whose eigenfunction is given by the Jacobi polynomial. In calculating the resolvent kernel, the sampling theorem [3] is fully employed. In Section 3, we first reexamine the FT of
whose eigenfunction is given by the Jacobi polynomial. In calculating the resolvent kernel, the sampling theorem [3] is fully employed. In Section 3, we first reexamine the FT of![]() , based on the resolvent for
, based on the resolvent for![]() . Then we compare the resolvent based method with other methods, to find that the former has some merits of being numerical calculation friendly and free of singularity for
. Then we compare the resolvent based method with other methods, to find that the former has some merits of being numerical calculation friendly and free of singularity for![]() , even after analytic continuation. Analytic property is signi- ficant for calculating, for example, path integral in Minkowski space (Wick roration), and the Shannon entropy in the limit of the Rényi entropy (replica trick). We give conclusion in Section 4.
, even after analytic continuation. Analytic property is signi- ficant for calculating, for example, path integral in Minkowski space (Wick roration), and the Shannon entropy in the limit of the Rényi entropy (replica trick). We give conclusion in Section 4.
2. Methods
In this section, we first obtain the resolvent kernel for the Hamiltonian whose eigenfunction is given by the Jacobi polynomial. Then we calculate the resolvent kernel for ![]() as a specialization of the former.
as a specialization of the former.
2.1. Jacobi Polynomial
Let ![]() (where
(where![]() ) be the Hamiltonian
) be the Hamiltonian
![]()
The (normalized) eigenfunction for ![]() is given by
is given by
![]()
where ![]() and
and ![]() represent the Jacobi polynomial and its normalization constant as
represent the Jacobi polynomial and its normalization constant as
![]() (3)
(3)
![]()
with ![]() and
and ![]() the Gamma function and the hypergeometric function, respectively. The corresponding eigenvalue is given by
the Gamma function and the hypergeometric function, respectively. The corresponding eigenvalue is given by
![]() (4)
(4)
The resolvent kernel for ![]() (denoted by
(denoted by![]() ) can be expanded using the eigenfunctions
) can be expanded using the eigenfunctions![]() ’s (for
’s (for![]() ) as
) as
![]() (5)
(5)
where in the second and third equalities, use has been made of the completeness for ![]() and (4), respectively.
and (4), respectively.
There seems to be no such formula as the series sum of (5) for general parameters ![]() and
and![]() . However, it will be found that the sum can be represented as the product of two hypergeometric functions as follows. The starting point would be the following formula, which corresponds to the particular case of
. However, it will be found that the sum can be represented as the product of two hypergeometric functions as follows. The starting point would be the following formula, which corresponds to the particular case of ![]() as [4] [5]
as [4] [5]
![]() (6)
(6)
where![]() . Notice that
. Notice that ![]() is given by the Legendre function
is given by the Legendre function ![]() as
as
![]()
where ![]() is defined by replacing
is defined by replacing ![]() in (3) with
in (3) with![]() . Before proceeding further, we discuss the validity of (6). By applying
. Before proceeding further, we discuss the validity of (6). By applying ![]() to (6) from the left, it is found that both sides of (6) satisfy the same second order differential equation for
to (6) from the left, it is found that both sides of (6) satisfy the same second order differential equation for![]() , due to the completeness relation of
, due to the completeness relation of![]() . The reason of restricting
. The reason of restricting ![]() to
to ![]() is as follows. To avoid the singularity of
is as follows. To avoid the singularity of ![]() at
at![]() ,
, ![]() should be restricted to either
should be restricted to either ![]() or
or![]() . Moreover, to avoid the singularity of
. Moreover, to avoid the singularity of ![]() (for
(for![]() ) at
) at![]() , the region of
, the region of ![]() is not allowed.
is not allowed.
Furthermore, it should be noted that the left-hand side of (6) turns out to be![]() , due to the relation
, due to the relation
![]()
Thus the relation of (6) can be rewritten as
![]() (7)
(7)
where![]() , so that the sampling theorem [3] can be applied to
, so that the sampling theorem [3] can be applied to![]() . The sampling theorem states that for
. The sampling theorem states that for ![]()
![]() (8)
(8)
where ![]() represents the support. Hence the validity of (7) is guaranteed by showing that
represents the support. Hence the validity of (7) is guaranteed by showing that ![]() for
for ![]() (with
(with![]() ). To show it, it is convenient to use the integral representation for
). To show it, it is convenient to use the integral representation for ![]() as [6]
as [6]
![]()
from which it is found that ![]() is vanishing for
is vanishing for ![]() under
under
the conditions of ![]() and
and![]() . Here, we have used the integral representation for the Dirac delta as
. Here, we have used the integral representation for the Dirac delta as![]() . Noticing further that
. Noticing further that
![]()
we can eventually prove the relation of (7) by employing the sampling theorem.
Before proceeding further, we try to rewrite the summation relation in the right- hand side of (8) in terms of the Dirac notation as
![]() (9)
(9)
where ![]() and
and
![]()
from which we obtain the orthonormality relation ![]() for all
for all![]() . The relation of (9) implies that the completeness relation
. The relation of (9) implies that the completeness relation ![]() holds, provided
holds, provided
it is applied to ![]() such that
such that![]() . Moreover, interpreting
. Moreover, interpreting ![]() and
and ![]() as
as ![]() and
and![]() , respectively, we can formally obtain from (9)
, respectively, we can formally obtain from (9)
![]() (10)
(10)
where ![]() represents the window function as
represents the window function as
![]()
The relation of (10) should be compared with
![]() (11)
(11)
[In the usual Dirac notation, ![]() is reserved for a Fourier transformed variable, so that
is reserved for a Fourier transformed variable, so that ![]() may be simply written as
may be simply written as![]() . Actually, if we formally write
. Actually, if we formally write ![]() as
as![]() , it is found that
, it is found that![]() , because
, because
![]()
where use has been made of the unitarity of ![]() as
as![]() . In this sense,
. In this sense, ![]() can be simply written as
can be simply written as![]() .] Notice that (10) cannot be derived from (11) by formally setting
.] Notice that (10) cannot be derived from (11) by formally setting ![]() to
to![]() . This is because
. This is because ![]() in (10) can be applied only to
in (10) can be applied only to ![]() such that
such that![]() . Notice further that the following relation can be derived from (10):
. Notice further that the following relation can be derived from (10):
![]() (12)
(12)
where we have used![]() . The relation of (12) indicates that the completeness relation
. The relation of (12) indicates that the completeness relation ![]() holds, if it is applied to
holds, if it is applied to ![]() such that
such that
![]() , so that
, so that![]() . These completeness relations, along with the orthogonal relations, are recapitulated in Table 1, while some examples of
. These completeness relations, along with the orthogonal relations, are recapitulated in Table 1, while some examples of ![]() satisfying (9) are listed in Table 2.
satisfying (9) are listed in Table 2.
Now we go back to generalize the relation of (6). Using the integral representation for ![]() (notice that
(notice that![]() ) as [7]
) as [7]
![]()
![]()
Table 1. Orthogonal relation and completeness relation, where![]() .
.
a![]() can be applied to
can be applied to ![]() such that
such that![]() . b
. b![]() can be applied to
can be applied to ![]() such that
such that![]() .
.
where![]() , we find that
, we find that ![]() in Table 2 can be generalized to
in Table 2 can be generalized to
![]() , and more generally to
, and more generally to ![]() (for
(for![]() , due to
, due to![]() ). As a special case of
). As a special case of ![]() in (9), we obtain
in (9), we obtain
![]() (13)
(13)
where![]() , with
, with ![]() (notice that for
(notice that for![]() , it turns out that
, it turns out that ![]() is given by a polynomial with respect to
is given by a polynomial with respect to![]() ). For
). For![]() , representing the Gegenbauer function, we have the following relations:
, representing the Gegenbauer function, we have the following relations:
![]()
and
![]()
Then it is found that the sum over ![]() in the right-hand side of (13) can be replaced by the sum over
in the right-hand side of (13) can be replaced by the sum over ![]() as
as
![]() (14)
(14)
where use has been made of ![]() for all
for all![]() . Once we have replaced the right-hand side of (13) by that of (14), it is not necessary to restrict the
. Once we have replaced the right-hand side of (13) by that of (14), it is not necessary to restrict the
parameter ![]() to either
to either ![]() or
or![]() . This is because
. This is because ![]() and the right- hand side of (14) satisfy the same second order differential equation for
and the right- hand side of (14) satisfy the same second order differential equation for![]() , de- spite the value of
, de- spite the value of![]() . By re-parameterizing
. By re-parameterizing ![]() in the right-hand side of (14) as
in the right-hand side of (14) as![]() , the relation of (6) is generalized to
, the relation of (6) is generalized to
![]() (15)
(15)
where use has been made of ![]() for all
for all![]() .
.
The relation of (15) can be further generalized. Recall that ![]() in Table 2 can be generalized to
in Table 2 can be generalized to![]() , which is proportional to
, which is proportional to
the Jacobi function. Following an analogous procedure for manipulating the Gegen- bauer function ![]() above, we finally obtain [1]
above, we finally obtain [1]
![]()
where use has been made of the relation
![]()
Notice the the superscripts ![]() in the left-hand and right-hand sides are ex- changed.
in the left-hand and right-hand sides are ex- changed.
2.2. Hermite Polynomial
In this subsection, we obtain the resolvent kernel for![]() , whose eigenfunction is given by the Hermite polynomial
, whose eigenfunction is given by the Hermite polynomial![]() . Considering that
. Considering that ![]() can be given by the specialization of the Gegenbauer polynomial
can be given by the specialization of the Gegenbauer polynomial ![]() as [8]
as [8]
![]() (16)
(16)
then we obtain from (15), together with the asymptotic expansion as ![]() (for
(for![]() ), the following formula:
), the following formula:
![]() (17)
(17)
where ![]() (
(![]() amounts to the normalization constant as
amounts to the normalization constant as ![]() ). Here,
). Here, ![]() , which is formally given by
, which is formally given by ![]() in (16), is related to the parabolic cylinder function
in (16), is related to the parabolic cylinder function ![]() as
as
![]()
where
![]()
with![]() , the confluent hypergeometric function. Considering that
, the confluent hypergeometric function. Considering that ![]() (for
(for![]() ) due to
) due to![]() , and that
, and that
![]()
where![]() , we find that the sum over
, we find that the sum over ![]() in the left-hand side of (17) can be formally extended to all
in the left-hand side of (17) can be formally extended to all![]() . Thus,
. Thus, ![]() satisfies the relation of (9) for
satisfies the relation of (9) for ![]() (listed in the fourth row in Table 2).
(listed in the fourth row in Table 2).
For later convenience, we divide the left-hand side of (17) into even and odd parts as
![]()
Recalling that ![]() for all
for all![]() , we obtain from (17)
, we obtain from (17)
![]() (18)
(18)
where use has been made of the following formulae:
![]()
The condition of ![]() comes from the intersection of
comes from the intersection of ![]() and
and![]() . To obtain
. To obtain ![]() for
for ![]() (complementary to
(complementary to![]() ), it may be conve- nient to rewrite
), it may be conve- nient to rewrite ![]() using another confluent hypergeometric function
using another confluent hypergeometric function ![]() as
as
![]() (19)
(19)
Substituting (19) into (18), and using ![]() again, we obtain the relation that is valid not only for
again, we obtain the relation that is valid not only for ![]() but also for
but also for ![]() in the form
in the form
![]() (20)
(20)
which was derived from a somewhat more straightforward approach [1] .
In a practical application, it is convenient to choose the parameter ![]() so that the
so that the ![]() -dependence of
-dependence of ![]() may be written as simply as possible. Considering that
may be written as simply as possible. Considering that ![]() is given by a polynomial of
is given by a polynomial of ![]() of order
of order![]() , we can choose
, we can choose ![]() as 0 for
as 0 for![]() . In the case of
. In the case of![]() , however,
, however, ![]() cannot be chosen as 0, due to the divergence of
cannot be chosen as 0, due to the divergence of![]() , but can be chosen as 1. To summarize, we have
, but can be chosen as 1. To summarize, we have
![]()
where![]() . No such formula as (20) but
. No such formula as (20) but ![]() has been listed in Ref. [9] .
has been listed in Ref. [9] .
At the end of this subsection, we deal with the sampling-theorem based summation formula for a single Hermite function of the form
![]()
where the coefficient ![]() is to be determined in such a way that the sum over
is to be determined in such a way that the sum over ![]() in the left-hand side can be formally extended to all integers, namely,
in the left-hand side can be formally extended to all integers, namely, ![]() (for
(for![]() ). Bearing the specialization of (16) in mind, we find that the corresponding summation formula for a single Gegenbauer function is given by
). Bearing the specialization of (16) in mind, we find that the corresponding summation formula for a single Gegenbauer function is given by
![]() (21)
(21)
Actually, the left-hand side of (21) can be rewritten as
![]()
where use has been made of![]() , and
, and ![]() for
for![]() . Under the specialization of (16), we finally obtain from (21)
. Under the specialization of (16), we finally obtain from (21)
![]() (22)
(22)
where ![]() for
for![]() . The condition of
. The condition of ![]() in (22)
in (22)
originates from the condition of ![]() in (21), which is equivalent to
in (21), which is equivalent to![]() , with
, with ![]() (corresponding to the case of
(corresponding to the case of ![]() in the first row in Table 2). The relation of (22) is listed in Ref. [10] , in which
in the first row in Table 2). The relation of (22) is listed in Ref. [10] , in which ![]() is given by using the parabolic
is given by using the parabolic
cylinder function![]() . [
. [![]() in [10] should be read as
in [10] should be read as![]() .]
.]
3. Results and Discussion
In this section, we first deal with the FT based on the resolvent for![]() . In a matrix representation of
. In a matrix representation of ![]() as
as
![]()
the supercharge ![]() can be written as
can be written as
![]() (23)
(23)
where ![]() and
and![]() . The corresponding SUSY Hamiltonian
. The corresponding SUSY Hamiltonian ![]() is given by
is given by
![]()
which amounts to![]() , where
, where ![]() (
(![]() can be simply denoted by
can be simply denoted by![]() , because
, because ![]() commutes with all the elements generated by
commutes with all the elements generated by![]() , and
, and![]() ). Under the transformation
). Under the transformation![]() , it is natural to transform FT as
, it is natural to transform FT as
![]() (24)
(24)
In this case, ![]() turns out to be unitary due to the self-adjointness of
turns out to be unitary due to the self-adjointness of![]() , and is related to
, and is related to ![]() through
through
![]() (25)
(25)
By the commutativity![]() , so is
, so is![]() , it follows from (23) and (25) that
, it follows from (23) and (25) that
![]() (26)
(26)
where the second relation can de derived from the conjugate of the first relation (recall that ![]() is unitary, so that
is unitary, so that![]() ).
).
The resolvent for ![]() can be written using
can be written using ![]() as
as
![]() (27)
(27)
The validity of (27) is verified by![]() . Recall that in Section 2, a convenient choice of the resolvent parameter
. Recall that in Section 2, a convenient choice of the resolvent parameter ![]() in
in ![]() is given by 0 (or 1) for an odd (or even) function. This corresponds to the choice of
is given by 0 (or 1) for an odd (or even) function. This corresponds to the choice of ![]() in (27) as 1, with
in (27) as 1, with ![]() to which
to which ![]() is applied being given by
is applied being given by
![]() (28)
(28)
where![]() . It should be noted that the
. It should be noted that the ![]() in (28) is the eigenfunction of
in (28) is the eigenfunction of![]() , with its eigenvalue being unity, that is
, with its eigenvalue being unity, that is
![]() (29)
(29)
where ![]() represents the space inversion
represents the space inversion
![]()
The relation ![]() can be formally derived from
can be formally derived from ![]() and
and ![]() , together with
, together with ![]() for all
for all![]() .
.
As a simple application, let us reconsider the FT of![]() , in which
, in which![]() .
.
Although the ![]() in this case does not belong to
in this case does not belong to![]() , we can formally apply
, we can formally apply ![]() to
to![]() , with the result that
, with the result that ![]() can be Fourier transformed. A series of calculations yields
can be Fourier transformed. A series of calculations yields
![]()
where the ![]() 's (for
's (for![]() ) are given by
) are given by
![]() (30)
(30)
For![]() , see Table 3.
, see Table 3.
Notice that ![]() for
for![]() , as is expected from the property that
, as is expected from the property that ![]() behaves like the multiplication by
behaves like the multiplication by ![]() in the limit of
in the limit of![]() . Bearing in mind that we have the relation
. Bearing in mind that we have the relation
![]()
by the commutativity![]() , so that
, so that![]() , then we again obtain
, then we again obtain
![]() (31)
(31)
Recalling that ![]() is an odd function of
is an odd function of![]() , we find that the first (second) element in
, we find that the first (second) element in ![]() (for
(for![]() ) in (30) is given by an odd (even) function. It should be noticed that this property holds for a general
) in (30) is given by an odd (even) function. It should be noticed that this property holds for a general ![]() in (28), not necessarily for
in (28), not necessarily for
![]() . The reason is as follows. From
. The reason is as follows. From![]() , together with (29), it is re- quired that
, together with (29), it is re- quired that
![]()
where![]() , projection on the even or odd parity space. Thus, it is found that the first (second) element in
, projection on the even or odd parity space. Thus, it is found that the first (second) element in ![]() is parity odd (even).
is parity odd (even).
In the latter half of this section, we discuss the FT of ![]() in another method. Some may point out that the result of (31) can be derived more efficiently from a method where
in another method. Some may point out that the result of (31) can be derived more efficiently from a method where ![]() is replaced by
is replaced by
![]() (32)
(32)
which is schematically shown as
![]()
Rewriting (26) as
![]() (33)
(33)
we find that ![]() can be chosen as such that depends on
can be chosen as such that depends on ![]() only (so that
only (so that ![]() depends on
depends on ![]() only), in order to calculate
only), in order to calculate ![]() in quite a simple way (we call such a case a classical method). To further simplify the calculation by
in quite a simple way (we call such a case a classical method). To further simplify the calculation by![]() , the functional form of
, the functional form of ![]() is given by a polynomial of
is given by a polynomial of![]() . Considering the condition of
. Considering the condition of![]() , we find that the simplest form of
, we find that the simplest form of ![]() and
and ![]() can be written as
can be written as
![]()
The calculation of![]() , and
, and ![]() is summarized in Table 3, together with the corresponding calculation in another classical (named classical 2, discussed in the next-next paragraph) and the resolvent methods.
is summarized in Table 3, together with the corresponding calculation in another classical (named classical 2, discussed in the next-next paragraph) and the resolvent methods.
Although all the methods give the same result as (31), there is an essential difference in ![]() between the classical 1 and resolvent methods from an analytical point of view. While
between the classical 1 and resolvent methods from an analytical point of view. While ![]() is an entire function,
is an entire function, ![]() has a pole at
has a pole at![]() . The non-analyti- city of
. The non-analyti- city of ![]() in the classical method is revealed when the
in the classical method is revealed when the ![]() is evaluated as
is evaluated as ![]() in the limit of
in the limit of![]() :
:
![]()
where ![]() is given by
is given by
![]()
In calculating ![]() from the inverse FT of
from the inverse FT of![]() , the limit operation
, the limit operation ![]() is necessary, because (inverse) FT is given by an improper integral. After the analytic continuation of
is necessary, because (inverse) FT is given by an improper integral. After the analytic continuation of ![]() and
and ![]() from
from ![]() to
to![]() , it is found that
, it is found that
![]() (34)
(34)
where![]() . Actually, for
. Actually, for![]() , for simplicity, we have
, for simplicity, we have
![]()
where![]() , so that it is confirmed that the relation of (34) holds for
, so that it is confirmed that the relation of (34) holds for![]() . Notice that
. Notice that ![]() is an entire function, because
is an entire function, because ![]() has a compact
has a compact
support so that its (inverse) FT turns out to be an entire function. Thus it is found that whether or not the relation of ![]() holds for all
holds for all ![]() depends on the property that
depends on the property that ![]() is an entire function (the identity theorem in complex analy- sis).
is an entire function (the identity theorem in complex analy- sis).
Some may further point out that in the classical method, ![]() for
for ![]() can be made an entire function by choosing
can be made an entire function by choosing ![]() [hence
[hence ![]() by (33)] as
by (33)] as
![]()
in which a series of calculations is summarized in Table 3. Although the ![]() is indeed an entire function, it is hard enough to calculate
is indeed an entire function, it is hard enough to calculate ![]() from
from ![]() (especially in a numerical way), compared to the resolvent method, because
(especially in a numerical way), compared to the resolvent method, because ![]() includes an infinite number of derivatives. Even if we try to regard
includes an infinite number of derivatives. Even if we try to regard ![]() as an integral transform, it fails due to the divergence of the corresponding integral kernel
as an integral transform, it fails due to the divergence of the corresponding integral kernel![]() . Actually, we obtain from
. Actually, we obtain from ![]()
![]()
which indicates that ![]() (for
(for![]() ) is divergent in a usual sense.
) is divergent in a usual sense.
Regarding the analyticity and numerical simplicity in calculating FT of![]() , it seems that, based on the above discussion, there is no way other than the resolvent based method.
, it seems that, based on the above discussion, there is no way other than the resolvent based method.
4. Conclusions
We have obtained, using the resolvent for the harmonic oscillator Hamiltonian![]() , the FT of a non-integrable function
, the FT of a non-integrable function![]() , such as
, such as![]() . As compared with the classical methods in Table 3, the resolvent method has some merits of being numerical calcula- tion friendly and free of singularity for
. As compared with the classical methods in Table 3, the resolvent method has some merits of being numerical calcula- tion friendly and free of singularity for![]() . In calculating the resolvent kernel, the sampling theorem is of great use. The introduction of SUSY to
. In calculating the resolvent kernel, the sampling theorem is of great use. The introduction of SUSY to ![]() not only makes transparent the usefulness of the even-odd decomposition of the
not only makes transparent the usefulness of the even-odd decomposition of the ![]() in a more natural way, but also leads to a natural definition of SUSY FT.
in a more natural way, but also leads to a natural definition of SUSY FT.
For future study, various extensions of the present work are possible. One extension is to deal with other unitary transforms, for example, the Hankel transform, whose eigenfunction is given by the Laguerre polynomials Using the resolvent for the corres- ponding Hamiltonian, we can obtain an analogous result. Another is to generalize ![]() to
to![]() , the Clifford algebra over
, the Clifford algebra over ![]() [
[![]() in (28) cor- responds to
in (28) cor- responds to![]() ]. Although the Clifford FT, in itself, is defined in various ways [11] [12] [13] [14] , mainly due to the non-commutativity of the algebra, the resolvent based calculation will still be of use, despite the non-commutativity.
]. Although the Clifford FT, in itself, is defined in various ways [11] [12] [13] [14] , mainly due to the non-commutativity of the algebra, the resolvent based calculation will still be of use, despite the non-commutativity.
Acknowledgements
The author is indebted to H. Fujisaka for useful discussions. This work was supported in part by HCU grant.