Improving Curve Number Runoff Estimates Using Dual Hydrologic Soil Classification and Potential Contributing Source Areas Delineation Methods ()
1. Introduction
Water reaches a stream by a variety of mechanisms, including direct precipitation, overland flow, shallow subsurface flow, and base flow. Overland flow is generated by two main processes: infiltration excess flow and saturation excess flow. Infiltration excess models are based on the soil’s infiltration capacity. When precipitation rates exceed the infiltration capacity, then overland flow is assumed to occur. Saturation excess models assume once soil storage has rea- ched capacity, then overland flow will occur. The two methods differ not only in the mechanisms of how overland flow is generated, but also the types of events that generate runoff and the locations within a watershed where overland flow is most likely to be generated first. In infiltration excess models, high intensity events of short duration will likely generate overland flow in higher sloped areas where the soil is thin or clay is present. Runoff in saturation excess models is likely to occur during gentle, longer duration events in low lying areas such as valleys where the soil layer is well developed.
Storm hydrographs are separated into two components: direct runoff and base flow. The direct runoff category consists of the combination of direct precipitation, overland flow, and shallow subsurface flow. Direct precipitation is usually assumed to be a negligible contribution to direct runoff. Depending upon basin characteristics, usually overland flow is considered to be the largest contributor to direct runoff, and most runoff models focus on this aspect of direct runoff [1] .
The Natural Resource Conservation Service (NRCS), formerly known as the Soil Conservation Service, curve number model is an empirical model that conceptually is intended to represent direct runoff (direct precipitation, overland flow, shallow subsurface flow) and can contain both saturation and infiltration excess processes. The curve number model assumptions and development have a bias toward saturation excess processes. This bias was noted by its developer Victor Mockus [2] [3] . To examine this bias, we present the model and assumptions in detail.
Rainfall excess (R) is considered to occur when
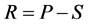 (1)
(1)
where P is rainfall volume and S is storage volume (both on and in the soil). If we develop an ideal proportional relationship, then
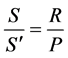 (2)
(2)
Such that S is the storage available, 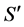 is the storage at saturation, R is the rainfall excess, and P is the precipitation volume (where all values are in mm). Equation (2) relates the precipitation volume to the storage at saturation. If we solve equation 1 for S and substitute into Equation (2), then we obtain the following:
is the storage at saturation, R is the rainfall excess, and P is the precipitation volume (where all values are in mm). Equation (2) relates the precipitation volume to the storage at saturation. If we solve equation 1 for S and substitute into Equation (2), then we obtain the following:
 (3)
(3)
 (4)
(4)
The CN values, which are empirical tabular values, are used to calculate S (in mm) by the following Equation (Equation 5):
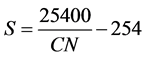 (5)
(5)
The tabulated CN values are based on hydrologic soil type and land cover. The simplicity of the model, the low number of variables, and endorsement by the USDA have made the CN model so readily accepted that use of the model has been augmented from its 1956 aims of calculating runoff from agricultural watersheds in the Midwest to calculating runoff in drylands or urban centers.
Variations and augmentations to the CN model tend to focus on improving its ability to better account for soil infiltration and antecedent soil moisture. Some observations about the mechanics of Equations (4) and (5) are of interest to this discussion of soil moisture and infiltration. Once S is calculated from the CN model the assumption is that if there is room within the soil matrix (represented as S), precipitation from the storm will go into storage. Additionally, the precipitation variable is depth of the total storm, not the intensity.
The CN model indirectly acknowledges infiltration rate and precipitation intensity in the hydrologic soil type classification and rainfall distribution. Hydrologic soils are one of the two main variables that affect the value of CN. Hydrologic soils are divided into four classes of infiltration rates, A, B, C, and D, where A type soils have the highest infiltration rates and are usually associated with sandy type soil textures and D type soils have the lowest infiltration rates and are usually associated with clay type soils. Hydrologic soils also have dual classifications: A/D, B/D, and C/D. The first classification refers to conditions of drained areas and the second refers to undrained areas.
Group A hydrologic soils have a saturated hydraulic conductivity (Ksat) in excess of 40.0 μm/sec, with a depth to restrictive layer of at least 50 cm and a depth to water table of at least 60 cm. Type B hydrologic soils have a Ksat value of between 10 and 40 μm/sec within at least 50 cm above any restrictive layer and depth to water table of at least 60 cm or Ksat of 4 - 10 μm/sec and depth to water table of 100 cm or greater. These soils are associated with moderately low runoff potential. Type C soils have a moderately high runoff potential and are classified by having a Ksat value of 1 - 10 μm/sec with at least 50 cm above a restrictive layer and 60 cm above the water table. Soils with greater than 100 cm depth to water table are considered type C if they have a Ksat value of 0.40 - 4 μm/sec. Type D soils have the highest runoff with a depth to restrictive layer of less than 50 cm and a depth to water table of less than 60 cm [4] . Dual hydrologic soil groups exist for type D soils that can be adequately drained [4] . These groups consist of A/D, B/D and C/D based on their Ksat value and the depth to water table when drained.
A second way precipitation and infiltration intensity are considered is through the NRCS National Oceanic and Atmospheric Administration (NOAA) rainfall distribution curves. These curves divide storm types into four types, Type I and IA, which are low intensity but long duration events, Type II intense short duration events, and Type III large volume events. Most of the United States outside of coastal areas is considered to have a Type II rainfall distribution. This consideration is quite coarse and is not meant to account for infiltration intensity in any amount of detail.
The above methods rely upon adjusting the CN for different conditions. Another method to improve the NRCS CN method is to adjust Ia percentages of S. Workers have found the Ia values to be less than 0.2S for A and B soils in urban settings [5] . Mishra et al., 2006 investigated Ia as a function of antecedent precipitation and its impacts on antecedent moisture. The general consensus within published studies is that Ia values are generally found to be less than those recommended by the model of 0.2S by as much as an order of magnitude [6] .
An added complexity to the issue of modeling runoff exists in regions with internal drainage. This is particularly the case in regions that have wetlands or karst topography. Watersheds are most often delineated by filling sinks in the elevation spatial data, also known as digital elevation models (DEM). These sinks may be errors within the DEM or represent depression features within the watershed. Watershed delineation that fills in sinks is common and an automated process within many Geographic Information System (GIS) software packages including ArcMap 10.2. The fill method works well for approximately 70 percent of the watersheds within the U.S.
For those regions, like the glaciated portions of the Midwest, internal drainage can make up a substantial portion of a watershed. If these internally drained portions of the watershed are “filled” and included, the NRCS CN model will overestimate runoff. Troolin and Clancy, 2016 examined ten watersheds in Wis- consin using three different delineation methods: the standard method of filling in sinks compared to two different models that did not fill in sinks and accounted for them differently. They found that overall there was not a significant difference between the models’ ability to account for runoff, except in the case of larger storms (>100 mm).
Troolin and Clancy, 2016 did not compare drained versus undrained areas (the dual hydrologic soil classification mention above). In particular, areas near wetlands have high water tables and often are not well drained areas. Even for the watershed delineation methods that excluded sinks from the delineated region, the areas adjacent to internal drainage would remain [7] .
In this study we expand upon the Troolin and Clancy, 2016 by adding eight watersheds to the original ten for a total of eighteen watersheds and by examining the hydrologic soil dual classification impact on the NRCS CN runoff results to match observed storms within gaged watersheds. We compared the drained hydrologic classification to the undrained classification for three delineation methods: one that fills all sinks, one that removes all sinks, and one that only includes the landscape that is directly connected to the floodplain. Our rationale for the study is that the dual classification will better highlight the differences in the accuracy of the modeled CN runoff compared to the runoff obtained from USGS gages [7] .
2. Study Area
The study area consists of 18 watersheds in Wisconsin: eleven in the south, five in the north central and two in the northeast portion of the state (Figure 1). The watersheds chosen are located in karst regions as well as glaciated regions and flat outwash plains. All of these land features are associated with the presence of wetlands and lakes in the topography that are considered areas of internal drainage, or sinks. Watersheds in these areas may not be accurately represented
![]()
Figure 1. Map of watersheds in study area.
using a watershed delineation method that fills in sinks [8] . Watersheds were selected based upon the following criteria: 1) ten years of USGS gaging station daily flow observations; 2) ten years of corresponding daily precipitation data from NOAA near the USGS gage; and 3) a range of land cover types.
3. Methods
3.1. Delineation Methods
Digital Elevation Models (DEM) are a required input into all three delineation methods. The DEMs used in this study are products of the USGS National Elevation Dataset (NED) and are of a ten-meter resolution [9] . The standard fill method (SFM) is part of the Hydrology Toolbox in ArcMap 10.2 for watershed delineation. This toolbox is derived from the D8 flow direction algorithm published by Jenson, 1998 [10] and is a standard method used for watershed delineation [7] [11] [12] . The SFM is derived from a filled DEM and assumes that all areas inside the watershed boundary will contribute runoff to the outlet. The two methods being compared to the SFM in this study are the Cut Method (CM) and the Potential Contributing Source Areas Method (PCSAM). In this study areas identified by the SFM and not by the CM or PCSAM are considered internal drainage. The CM and PCSAM both attempt to account for internal drainage in different ways, but the PCSAM has significantly higher amounts of GIS input data required. A visual comparison of the three methods can be found in Figure 2.
The CM uses the output from the SFM and the original DEM. Using a tool called Raster Calculator in ArcMap, the SFM is subtracted from the original DEM. The Raster Calculator takes each cell in the DEM and subtracts each cell from the SFM. The result is a grid with cells containing zeros where the SFM and original DEM have the same value and negative values where the sinks had been filled during the process of the SFM. Any resulting negative values are eliminated from the delineation buy using the Reclassify Tool found in the Spatial Analyst Tool Kit. Using the Reclassify Tool, any negative value cells are assigned a value of “No Data” and any cells with a value of zero are assigned a value of 1. This reclassification allows the delineation to account only for areas where the filled DEM matched the unfilled DEM, thus eliminating sinks. This method does not change the shape or extent of the watershed boundary because it works within the extent
![]()
Figure 2. SFM, CM and PCSAM delineations for the Yahara River at McFarland, WI.
of the SFM. The watershed area is only decreased by the amount and spatial extent of the sinks that are eliminated. The CM is not considered to be data intensive because it can be done entirely within ArcMap using the Spatial Analyst Tool Kit and does not require any additional data inputs. The only additional steps a user must take are to create two additional grids; one as a product of the Raster Calculator and another as the final product of the CM after reclassification (Fig- ure 3).
The PCSAM is more complex than the SFM and CM in that it requires additional data and time. The delineation is performed in a way that is almost opposite of the SFM and CM. Whereas the SFM and CM delineate the watershed from the highest topographic points inward, the PCSAM delineates from the stream network outward. It does this by assuming that the land immediately adjacent to the stream network will contribute to runoff and that any areas upslope from the drainage network will also contribute. The method was developed by Richards and Brenner, 2004 [13] and was improved upon by Macholl et al., 2011 [14] , and Troolin, 2015 [15] .
The PCSAM is a FORTRAN program that operates outside of ArcMap to create a delineation based on raster data. Inputs to the program include two floating point rasters: a DEM of the watershed region and an Initial Contributing Area (ICA) raster. Both of these rasters need to have the same spatial extent, coordinate system, and cell size in order for the program to work properly. The ICA is created through a series of vector and raster operations and requires more data than just a DEM. The additional data required include streams, water bodies,
and wetland land cover. The data used in this study are the 1:24,000 scale digitized streams and water bodies from the Wisconsin Department of Natural Reso- urces [16] and the 30-meter resolution 2011 National Land Cover Data (NLCD) [17] [18] .
The ICA raster is built within ArcMap using the aforementioned data. Three polygon layers representing water bodies adjacent to streams, wetlands adjacent to streams, and a buffer around the stream network must be created before they can be merged together and converted to a raster that serves as the ICA, the second input into the PCSAM program.
To build the wetland polygons 2011 NLCD data [17] were extracted using the Extract by Mask Tool found in the Spatial Analyst Toolkit. The SFM delineation was used to set the spatial extent of the NLCD data extraction. The wetland land cover areas were identified using the Select by Attributes Tool, and these selected data were exported as a raster representing wetlands within the watershed. This wetland raster was then converted to a polygon feature class using the Raster to Polygon Tool within the Conversions Toolkit. The Select by Location Tool was used to determine which wetland polygons intersected the stream layer in order to export them to their own “intersecting wetlands” polygon feature class. Intersecting water bodies were also identified using the same tool and water bodies that intersected the stream layer were exported to an “intersecting water bodies” polygon feature class. The third polygon feature class was created using the Buffer Tool with a distance of fifty meters around the connected stream network creating a stream buffer that is 100 m across. These three polygon feature classes: intersecting wetlands, intersecting water bodies and the stream buffer were then merged together to create what is considered the ICA (Figure 4).
The ICA needed to be converted to a raster format with a spatial extent of the DEM. This was done with a series of vector and raster operations. First the ICA was given an additional attribute field named “PCSAM” that was assigned a value of one with the Field Calculator. Next the Create Constant Raster Tool from the Spatial Analyst Toolkit was used to create a raster covering the spatial extent of the DEM. The constant raster was then converted to a polygon feature class using the Raster to Polygon Conversion Tool found in the ArcMap 10.2 Data Management Toolkit. The “PCSAM” field was added to the newly created constant raster polygon attribute table and set to a value of zero. Next the ICA was erased from the constant raster polygon to create a space for the two to be merged together. This was done using the Erase Tool and then the Merge Tool (Figure 4), resulting in an ICA polygon feature class where the original ICA has a PCSAM value of one and the surrounding area has a value of zero (Figure 4).
The newly created ICA polygon feature class was converted to a raster using the Polygon to Raster Conversion Tool, where the PCSAM field was identified as the value to base the conversion on. The resultant ICA raster has values of one where the stream buffer, wetlands, and water bodies are represented and zeros in the surrounding area filling the spatial extent of the DEM. Both the ICA raster and the DEM were converted to floating point rasters in ArcMap using the Raster
![]()
Figure 4. Workflow for the PCSAM Method.
to Float Conversion Tool in preparation for the PCSAM program to be run outside of ArcMap.
The two floating point rasters were exported to the C drive in a folder with the PCSAM FORTRAN program, and the program was run through the command prompt window, set to do 400 iterations. The PCSAM program determines cell by cell which cells are sloping downward into the ICA and will therefore contribute runoff. While set to 400 iterations, the program will delineate up to 4000 meters from the ICA (with a 10 m DEM). The number of iterations can be ada- pted depending on conditions (e.g. topography). The output of the PCSAM program is an ASCII file that was imported back into ArcMap and converted to a raster using the ASCII to Raster Conversion Tool. The resultant PCSAM delineation is initially a raster covering the spatial extent of the DEM with ones in the cells that represent the delineation and zeros in the cells that represent the surrounding area. The final step in creating the PCSAM delineation is to use the Reclassify Tool to reclassify the zeros as “No Data” and the leave the cells with a value of one, which represent the delineation (Figure 4).
3.2. Using Curve Number to Calculate Runoff Volume
The spatial data used to create CN layers in this study were the 2011 NLCD dataset [17] and the 2003 Soil Survey Geographic Database (SSURGO) from the NRCS [19] NLCD has sixteen categories and is available in a 30-meter resolution for the entire United States (Homer et al., 2015). SSURGO data were available in vector form and had to be converted to raster with a 30-meter resolution to be compatible with the NLCD data. SSURGO has seven possible categories of hydrologic soils: A, B, C, D and three categories of dual hydrologic soil groups: A/D, B/D, and C/D [4] .
For the purpose of this study, a CN layer was created representing conditions of drained soils. The hydrologic soil groups used in the creation of this layer consisted of all seven soil types. A second CN layer, representing undrained soil conditions, changes the A/D, B/D, and C/D to type D soils. Each CN layer was used to calculate modeled runoff for all three delineations in order to see how the model responded in both a saturated and unsaturated scenario.
3.3. Storm Selection and Modeled Runoff Calculation
Curve number runoff was modeled with precipitation data having at least ten consecutive years of record and matching discharge data from USGS gauging stations to compare modeled values to observed [17] [20] . If more than one precipitation station was in the watershed, the precipitation values for each storm were calculated using the Theissen polygon method [1] . Precipitation data were sorted to isolate only summer months (June-September) in order to exclude freeze/thaw events.
For the modeled runoff calculated from a CN layer representing drained hydrologic soil conditions (with dual groups A/D, B/D and C/D), storms were selected by peak runoff from. During storm selection for modeling drained conditions, precipitation data was restricted to values within one standard deviation of the mean. When selecting storms to model runoff using the undrained hydrologic soil condition CN layer, storms were selected based on precipitation intensity and were unrestricted by standard deviation. Storm intensity was calculated using a Java program to identify storm events. The program identified storms that had at least two days prior with less than .02 cm precipitation, as well as two days after. The intensity values were generated by calculating the sum of precipitation per storm divided by the duration in days.
For each watershed 5 - 10 storms were identified. CN runoff was calculated using the delineation rasters to determine area and the CN runoff values for each pixel to determine depth per pixel in mm. These area and depth measurements were combined to generate modeled runoff volume in m3 in order to compare to runoff data. Discharge data were obtained from USGS gaging stations and values for runoff were obtained using the USGS Hydrograph Separation Program (HYSEP) [21] and the USGS Web Hydrograph Analysis Tool [22] .
3.4. Statistics
Total observed runoff data were derived from the hydrograph separation. The modeled runoff was determined by adding up the runoff values calculated from the curve number for each grid cell within the watershed delineation. The delineation methods produced different watershed area; therefore, we normalize the error by the SFM watershed area. This resulted in the following Equation:
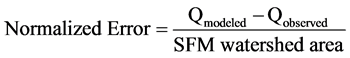 (6)
(6)
where Qmodeled is the runoff discharge calculated from the curve number model multiplied by the area (cubic meters) and Qobserved is the runoff discharged from the USGS gage and processed through a hydrograph separation (cubic meters). The SFM watershed area is in m2 resulting in normalized error in meters. To evaluate the difference in the model errors and watershed land use percent, we used a two tailed (alpha = 0.05) paired t-test comparing the SFM to the CM and PCSAM.
4. Results
For the eighteen watersheds within this study, the SFM watershed area ranged from 40 to 1575 km2 with an average of 520.53 (346 standard deviation) km2. The CM fraction of SFM ranged from 0.74 to 0.99 with an average of 0.93 (0.10 standard deviation), and the PCSAM fraction of SFM ranged from 0.14 to 0.91 with an average of 0.51 (0.27 standard deviation). The specific values of watershed area for each delineation are summarized in Table 1.
The major land use categories are summarized in Table 2 for each watershed
![]()
Table 1. Watershed area in square kilometers for SFM, CM and PCSAM delineations.
![]()
![]()
Table 2. Major land use percentages in SFM, CM and PCSAM.
by delineation method. For the SFM, agriculture represented the largest land use category (43%), followed by forest (33%), urban (12%) and wetland (7%). The CM and PCSAM land use differed the most from the SFM in the wetland land use category. On average the CM had a lower percentage of wetland land use by 50 percent in some watersheds, and the PCSAM had higher percentage of wetland use by 500 percent in some watersheds (see Table 2 for details).
We also compared observed runoff from the USGS gage to runoff calculated from the CN model. Figure 5(a) and Figure 5(b) illustrate the absolute value of the normalized error (see Equation (6)) for the precipitation values. In Figure 5(a) we use the drained hydrologic soil classification, and in Figure 5(b) we use the undrained hydrologic soil classification. In Figure 5(a) we find that for storm events less than 100 mm the three delineation methods do not perform statistically differently. For storm events larger than 100 mm we find the SFM and CM are not statistically different. In Figure 5(b) the PCSAM performed better than the SFM and CM, for both precipitation storms greater and less than 100 mm.
In Figure 6(a) and Figure 6(b), we show the relationship between percent forest cover and absolute value of normalized error for the drained (a) and undrained (b) hydrologic soil types. In general, the overall trend is that as forest cover increases, the absolute value of the normalized error decreases. With higher percent forest (> 40%) the PCSAM method performs better than the other models using the undrained hydrologic soil type. For lower percent forest, the delineation methods are not statistically different.
Figure 7(a) and Figure 7(b), illustrate the relationship between percent wetland cover for the drained (a) and undrained (b) hydrologic soil types. In general, the overall trend is similar to that of the forest land cover, in that as wetland cover increases, the absolute value of the normalized error decreases. The PCSAM method performs better than the other models using the undrained hydrologic soil type. Using the drained soil assumption, we find that there is not a statistical difference between the methods.
Finally, in Figure 8(a) and Figure 8(b), we show the relationship between percent agricultural land cover for the drained (a) and undrained (b) hydrologic soil types. In general, the overall trend is the opposite of that of forest and wetland cover, in that as agricultural land use increases, the absolute value of the normalized error increases. For agricultural land use greater than 30 percent, the PCSAM performs better for both the drained (Figure 8(a)) and undrained (Figure 8(b)) soil types. For the undrained hydrologic soil (Figure 8(b)) all delineation methods performed better with no statistical difference until agricultural coverage increases to 25 percent. With higher agricultural coverage, the PCSAM method performs better.
5. Discussion
The SFM and CM have similar land use, which may be an indicator that the ArcMap step of “filling” the DEM is associated with errors within the DEM and that the pixels “filled” are random and do not have bias toward a particular land cover type. Overall there is no significant different between the SFM and CM land use percentages (p-value > 0.05). The wetland category is of particular interest because wetlands are known to represent areas of internal drainage [7] [14] . The PCSAM differs from SFM significantly (p-value < 0.05) in the areas of urban and wetland, which is to be expected because the PCSAM method uses the stream buffer and wetlands as input to the delineation method. Urban areas away from the stream with no direct connection to the drainage area would be excluded from the PCSAM. The results of the land cover percentages for the different watersheds indicate that the CM may simply be discarding areas within the watershed that are truly connected, and the process of filling pits may be appropriate.
Overall the PCSAM performance is better for larger storms (>100 mm), as shown in Figure 5(a) and Figure 5(b). This finding is similar to Troolin and Clancy, 2016; however, with the larger data set, the PCSAM was found to have a
![]() (a)
(a)![]() (b)
(b)
Figure 5. (a) Precipitation versus absolute value of normalized error for drained hydrologic soil types; (b) precipitation versus absolute value of normalized error for undrained hydrologic soil types.
normalized error 50% less for larger storms (compared to 3%). For smaller sto- rms (<100 mm), there was no statistical difference (p-value > 0.05). The normalized error trends for forest cover (Figure 6(a) and Figure 6(b)), wetland (Fig- ure 7(a) and Figure 7(b)), and agriculture (Figure 8(a) and Figure 8(b)) are also similar to Troolin and Clancy, 2016 with the exception of one important difference associated with using the dual hydrologic soil classification [7] . In Troolin and Clancy, 2016 there was no statistically significant difference (p- value > 0.05) between the delineation methods [7] . For this study, we found using the undrained hydrologic soil classification yielded very different results. The PCSAM had significantly lower error (p-value < 0.05) than the SFM and CM. In particular, for watersheds with higher percentages of forest, wetland, and agricultural land use, the PCSAM curve number model values were closer to observed values by 50 to 80 percent.
![]() (a)
(a)![]() (b)
(b)
Figure 6. (a) Percent forest land cover versus absolute value of normalized error for drained hydrologic soil types; (b) percent forest land cover versus absolute value of normalized error for undrained hydrologic soil types.
![]() (a)
(a)![]() (b)
(b)
Figure 7. (a) Percent wetland land cover versus normalized error with drained hydrologic soil types; (b) percent wetland land cover versus normalized error with undrained hydrologic soil types.
SFM and CM have similar land use, which may be an indicator that the ArcMap step of “filling” the DEM is associated with errors within the DEM and that the pixels “filled” are random and do not have bias toward a particular land cover type. Overall there is no significant different between the SFM and CM land use percentages (p-value > 0.05). The wetland category is of particular interest because wetlands are known to represent areas of internal drainage [7] [14] . The PCSAM differs from SFM significantly (p-value < 0.05) in the areas of urban and wetland, which is to be expected because the PCSAM method uses the stream buffer and wetlands as input to the delineation method. Urban areas away from the stream with no direct connection to the drainage area would be excluded from the PCSAM. The results of the land cover percentages for the different watersheds indicate that the CM may simply be discarding areas within the watershed that are truly connected, and the process of filling pits may be appropriate.
![]() (a)
(a)![]() (b)
(b)
Figure 8. (a) Percent agricultural land cover versus absolute value of normalized error for drained hydrologic soil types; (b) percent agricultural land cover versus absolute value of normalized error for undrained hydrologic soil types.
Overall the PCSAM performance is better for larger storms (>100 mm), as shown in Figure 5(a) and Figure 5(b). This finding is similar to Troolin and Clancy, 2016; however, with the larger data set, the PCSAM was found to have a normalized error 50% less for larger storms (compared to 3%). For smaller storms (<100 mm), there was no statistical difference (p value > 0.05).
6. Conclusions
Additionally, we have found that the SFM and CM are not significantly different, and methods to capture the contributing area of a watershed will not be improved by a CM. The PCSAM, which does require more processes, may be a better choice in regions with greater than 30 percent forest, wetland, or agriculture. In particular, the delineation performs very well for large precipitation events using an undrained hydrologic soil classification.
Acknowledgements
Thank you to William Troolin for use of his thesis data, to Jacob Burdick and Brandon Lee for watershed delineations, to Julie Schmock for data sorting and to Dale Miller for the creation of a Java program to sort storms by intensity. Thank you to Chandra Page for proofreading expertise.