Analysis of Wigner’s Set Theoretical Proof for Bell-Type Inequalities ()
1. Introduction
Einstein challenged the Copenhagen interpretation of quantum mechanics by pro- posing with Podolsky and Rosen [1] Gedanken-Experiments, briefly called EPR experi- ments. These experiments were to demonstrate that quantum mechanics is incomplete, having missed in its description of physical reality some elements of that reality.
About 30 years after the EPR paper, Bell [2] derived an inequality for functions of elements of physical reality, known since as Bell’s inequality, that in his opinion had to be obeyed by all of classical physics, meaning in essence by the framework of Einstein’s relativity. Wigner transformed Bell’s derivation into a set theoretical approach [3] .
The belief in (ii) arose mainly from the work of Wigner [3] and a popularized version of Wigner’s work by d’Espagnat [8] . (d’Espagnat, however, also uses counterfactual reasoning that raises additional questions [7] .) The fact that many EPR-types of experiments have been published that violate Bell’s and Wigner’s inequalities, is therefore presented as proof against the validity of Einstein’s local realism, because it appears inconceivable that set theory is incorrect.
As we will show, there exists an analogy to the Einstein-Poincaré discussions, because Wigner connected his mathematical sets to the actual measurements in a way that is inconsistent with the space-time physics of the actual EPR experiments. Key to our reasoning is the fact that the set of data of the actual measurements is necessarily involving space- and time- (or space-time-) coordinates to designate the correlated pairs. These sets of space and time coordinates are inconsistent with Wigner’s sets and subsets that are ordered according to location in three-dimensional space and equip- ment settings in that space, but do not involve measurement times.
We show in detail that Wigner’s derivation of Bell type inequalities (that restrict the possible correlations exhibited by EPR measurements) does actually not use Einstein’s local realism at all. Instead Wigner assumes in a hidden and unjustified way certain topological combinatorial properties of his mathematical sets that are inconsistent with the macroscopic properties of the measurement equipment in space and time as de- termined by clocks, protractors and meter-measures. The contradictions between Wigner’s (Bell-type) inequalities and well known experiments (see II B) must, therefore be blamed on Wigner’s topological-combinatorial assumptions and not on Einstein’s local realism.
To prove this finding, we first analyze the elements of physical reality used in EPR experiments and form the sets of physical elements that must be dealt with in Wigner’s mathematical proof (see Section 2). We then review the essential portion of Wigner’s mathematical proof and point to his unwarranted assumptions (see Section 3). Finally, in Section 4 we deduce from these latter assumptions the topological-combinatorial problems of Wigner’s work and conclude that the well known line “death by experi- ment” applies to Wigner’s theory not to Einstein’s. Our conclusions are summarized in Section 5.
2. Einstein’s Realism, EPRB Experiments and Their Resulting Data
We consider in the following only a variation of EPR experiments as suggested by Bohm and, therefore called EPRB experiments [10] [11] . This type of experiment involves the measurement of the two single entities of correlated pairs of particles. Each single entity is measured at a different set of space-coordinates. These space-coordi- nates must, from the viewpoint of physics, describe the entire local measurement equipment for both measurement locations. For brevity and because important mea- surements have actually been performed there, we will denote the two measurement locations and corresponding space coordinates just by “Tenerife” and “La Palma”. The space-like separation of the measurements is a necessity to invoke Einstein’s separation principle, which is an important factor of the EPR argument and focus of the EPR discussion. Einstein’s separation principle excludes all influences between the two measurement stations that are faster than the speed of light in vacuum. This principle guarantees a certain independence of the two separated measurement stations and represents the core of what is commonly called Einstein’s local realism. A broader discussion and detailed definition of Einstein’s local realism has been given by Fine [12] .
It is, therefore, of utmost importance for the discussions of Bell and Wigner to exclude in the actual experiments influences from the other location that propagate with speed slower or equal to that light. How can one make sure that there exist no such other influences and in addition that one indeed measures correlated pairs? This goal has been achieved in [10] , [11] and other experiments. These measurements relate to the Clauser-Horn-Shimony-Holt (CHSH) inequality. We note here, however, that all of our reasoning applies, as will become evident below, also to this type of inequality. We just discuss the Bell inequality in our analysis, because Wigner’s proof referred only to this type of inequality.
2.1. Switching Instruments and Pairing Particles
However, it is precisely this pairing and timing problem, where Einstein embedded the necessity of using a space-time system, his space-time system, as the basis for his Gedanken-Experiments and the theoretical approach with Podolsky and Rosen, [1] , [13] . There also exists no other known way to pair and correlate space like separated measurement outcomes than by space and time measurements.1
The timing of the measurements is, thus, a most important element of the physical reality, of the data, and we denote the clock-time of the 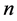 th measurement in Tenerife by
th measurement in Tenerife by 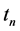 and that in La Palma by
and that in La Palma by . Note that subsequent measurement pairs are necessarily time-like separated because the switching of the macroscopic settings cannot be instantaneous. To identify actual correlated pairs, some rule needs to be employed that selects the pairs. An example of such a rule would be that the time difference of the measurements at the two different locations (islands) must be smaller than a certain value
. Note that subsequent measurement pairs are necessarily time-like separated because the switching of the macroscopic settings cannot be instantaneous. To identify actual correlated pairs, some rule needs to be employed that selects the pairs. An example of such a rule would be that the time difference of the measurements at the two different locations (islands) must be smaller than a certain value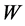 . We emphasize that through any such rule an instantaneous logical and physical connection is established between the measurements at the two different locations that has nothing to do with instantaneous influences, much less with information transfer. Without such a connection, no correlations between the space- like separated measurements can be established. Only with such a connection can intricate correlations due to physical law be revealed that now may involve also the many-body dynamics of the measurement equipment of both locations. It also must be emphasized that the analysis of the raw data of three different EPRB experiments [11] [14] [15] [16] do show a significant
. We emphasize that through any such rule an instantaneous logical and physical connection is established between the measurements at the two different locations that has nothing to do with instantaneous influences, much less with information transfer. Without such a connection, no correlations between the space- like separated measurements can be established. Only with such a connection can intricate correlations due to physical law be revealed that now may involve also the many-body dynamics of the measurement equipment of both locations. It also must be emphasized that the analysis of the raw data of three different EPRB experiments [11] [14] [15] [16] do show a significant 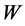 -dependence of the amount of violations of Bell-type inequalities (actually the CHSH inequality), for values of
-dependence of the amount of violations of Bell-type inequalities (actually the CHSH inequality), for values of 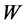 that are much smaller than the average time between the detection of photons [17] [18] .
that are much smaller than the average time between the detection of photons [17] [18] .
From what follows in this paper, it appears imperative to perform measurements that involve dependencies on the timing and on the instrument settings in relation to that timing.
Wigner ignored the measurement times and corresponding connections when considering possible and actual outcomes in his theory and we will see that this negligence has serious consequences for his set theoretic calculations of correlations.
2.2. Elements of Physical Reality: Notation and Notebook-Entries
Actual EPRB measurements (e.g. [10] [11] ) monitor, in addition to the clock-times of the detector events, two equipment orientations that determine the spin (polarization) of incoming particles. These registrations, for photons often obtained with polarizers and avalanche photodiodes, have been denoted by a variety of symbols such as 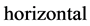 and
and 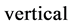 etc. and Wigner uses
etc. and Wigner uses 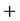 and
and  for any particles that he considers. We denote the measurement result for the
for any particles that he considers. We denote the measurement result for the 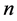 th measurement in Tenerife by
th measurement in Tenerife by 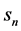 and that in La Palma by
and that in La Palma by 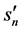 each being either
each being either  or
or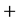 .
.
As mentioned, the atoms and molecules constituting the measurement equipment have many body interactions with the incoming particles, from both the view of Einstein’s physics and also from the most modern view of quantum physics. Nevertheless, both Bell, Wigner and all their followers describe this equipment, as the Copenhagen school of quantum mechanics does, just by a three-dimensional unit vector of space, indicating the direction of a polarizer or of a Stern-Gerlach magnet. We denote this unit vector for the nth experiment by 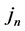 in Tenerife and
in Tenerife and 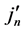 in La Palma, respectively. Wigner assumed that this unit vector may assume precisely the same three directions
in La Palma, respectively. Wigner assumed that this unit vector may assume precisely the same three directions 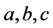 in both Tenerife and La Palma and that these directions are randomly chosen on each island in the actual experiments. Using these assumptions and notational conventions we arrive at EPRB notebook-entry pairs of the kind:
in both Tenerife and La Palma and that these directions are randomly chosen on each island in the actual experiments. Using these assumptions and notational conventions we arrive at EPRB notebook-entry pairs of the kind:
![]() (1)
(1)
where, as mentioned, both ![]() and
and ![]() may (exclusively) assume the value of either
may (exclusively) assume the value of either ![]() or
or ![]() and both
and both ![]() and
and ![]() are randomly chosen from the vectors
are randomly chosen from the vectors![]() . The parenthesis
. The parenthesis ![]() indicates the measurement of a correlated pair and the symbol “;” denotes the separation of entries for Tenerife and La Palma. The number 9 of the time-selected pairs thus could be represented by the following actual notebook entry
indicates the measurement of a correlated pair and the symbol “;” denotes the separation of entries for Tenerife and La Palma. The number 9 of the time-selected pairs thus could be represented by the following actual notebook entry![]() . As far as EPRB experiments are concerned such entries are collections of elements of physical reality (in the sense of Mach) and represent the only physical reality that we need to consider to discuss Wigner’s proof.
. As far as EPRB experiments are concerned such entries are collections of elements of physical reality (in the sense of Mach) and represent the only physical reality that we need to consider to discuss Wigner’s proof.
As mentioned, both Bell and Wigner use Einstein locality as a tool of reasoning: For carefully designed EPRB experiments they reason, that the measurement outcome ![]() does not depend on what vector
does not depend on what vector ![]() is chosen in La Palma and
is chosen in La Palma and ![]() does not depend on
does not depend on ![]() in Tenerife.
in Tenerife.
Wigner discussed in his paper three pairs of measurements with the given settings ![]() and
and![]() , exactly those that Bell had chosen for his inequality. Such a selection gives us the following six-tuple that we call henceforth Bell’s six-tuple:
, exactly those that Bell had chosen for his inequality. Such a selection gives us the following six-tuple that we call henceforth Bell’s six-tuple:
![]() (2)
(2)
Here![]() ,
, ![]() , and
, and ![]() where
where ![]() is a large number determined by the total number of measurements. The brackets
is a large number determined by the total number of measurements. The brackets ![]() indicates again the measurement of a correlated pair. If we assume that these pairs are derived from the notebook entries (1), then Einstein’s local realism does not put any constraint on the possible values of the pairs
indicates again the measurement of a correlated pair. If we assume that these pairs are derived from the notebook entries (1), then Einstein’s local realism does not put any constraint on the possible values of the pairs![]() ,
, ![]() and
and![]() . For given measurement times, they may assume any of the possible
. For given measurement times, they may assume any of the possible ![]() combinations of values of
combinations of values of ![]() and
and![]() , because from both a physical and mathematical point of view there are at this point no restrictions to the possible outcomes except that they are two-valued.
, because from both a physical and mathematical point of view there are at this point no restrictions to the possible outcomes except that they are two-valued.
For each pair, we are interested with Wigner in only two different possibilities when measuring on the individual particles: either equal outcomes or unequal outcomes. Therefore, for a string of ![]() measurements of pairs, we have
measurements of pairs, we have ![]() different possible outcomes. If we have three such strings of pairs we have
different possible outcomes. If we have three such strings of pairs we have ![]() possible different correlations of the pair outcomes. Wigner reduces the number of correlations that he considers essential significantly further, by counting only those that yield a different fraction of the final count of equal relative to unequal outcomes. Simple counting leads then to the conclusion that for each string of
possible different correlations of the pair outcomes. Wigner reduces the number of correlations that he considers essential significantly further, by counting only those that yield a different fraction of the final count of equal relative to unequal outcomes. Simple counting leads then to the conclusion that for each string of ![]() measurements of pairs we have
measurements of pairs we have ![]() different possible outcomes that lead to a different fraction of equal and unequal outcomes (see Table 1 for an illustration of the counting procedure). There- fore we obtain for the six-tuple (2)
different possible outcomes that lead to a different fraction of equal and unequal outcomes (see Table 1 for an illustration of the counting procedure). There- fore we obtain for the six-tuple (2)![]() , possible outcomes that Wigner counts as different.2
, possible outcomes that Wigner counts as different.2
As we have mentioned, Einstein’s local realism has not been used up to now. We show below that it also is not used in Wigner’s further considerations that lead to his variation of Bell’s inequality. Wigner’s theory does thus derive, without reference to Einstein locality, how many different correlations of equal and different outcomes may occur for the ![]() pairs of measurements. Nevertheless, Wigner’s number of possible different correlations is significantly reduced below the above mentioned value of
pairs of measurements. Nevertheless, Wigner’s number of possible different correlations is significantly reduced below the above mentioned value of ![]() and is only proportional to
and is only proportional to![]() .
.
We ask, therefore, the question: What caused the reduction of the possible number of correlations in Wigner’s proof? Our answer is that it was not any assumption regarding Einstein’s local realism. Instead, the reduction of the number of possible correlations arises from Wigner’s unwarranted mathematical assumption that is related to set
theoretic probability theory. The reduction of possible correlations is, therefore, artifi- cial and does not apply to EPR experiments. As mentioned, the celebrated line “death by experiment” is correct but it applies to Wigner’s theory and not, as reported in so many sensationalist articles, to Einstein’s.
3. Wigner’s Additional Assumptions
Wigner defines (p. 1007, left column last paragraph of [3] ) “domains of the space of the hidden variables” and claims (in agreement with our thinking about possible outcomes outlined above) that “we have only ![]() essentially different domains”. These can be characterized by symbols:
essentially different domains”. These can be characterized by symbols:
![]() (3)
(3)
all ![]() and
and ![]() assuming two possible values:
assuming two possible values: ![]() or
or![]() , and the
, and the ![]() referring to the first, the
referring to the first, the ![]() to the second, particle. Wigner’s detailed explanations also point out that the domains characterized by
to the second, particle. Wigner’s detailed explanations also point out that the domains characterized by ![]() correspond precisely to the respec- tive equipment-settings
correspond precisely to the respec- tive equipment-settings ![]() which leads to the 9 possible pairings (see Equaton (6) below) from which the possible pairs of Bell’s six-tuple (2) and possible outcomes (
which leads to the 9 possible pairings (see Equaton (6) below) from which the possible pairs of Bell’s six-tuple (2) and possible outcomes (![]() ,
,![]() and
and ![]() in our notation) can be selected.
in our notation) can be selected.
In the next paragraph Wigner states his most crucial assumption by a definition: “Let ![]() denote henceforth the probability that the hidden parameters assume, for the singlet state of the two spins, a value lying in the domain which was denoted by this symbol”. As innocuous as this definition looks, it contains a very big assumption, the assumption of the existence of a joint probability for the six-tuples (3) of possible outcomes of the measurements, while the actual measurements are only performed in pairs.
denote henceforth the probability that the hidden parameters assume, for the singlet state of the two spins, a value lying in the domain which was denoted by this symbol”. As innocuous as this definition looks, it contains a very big assumption, the assumption of the existence of a joint probability for the six-tuples (3) of possible outcomes of the measurements, while the actual measurements are only performed in pairs.
Wigner’s assumption about the joint probability of the domains of variables (parameters) that determine the possible outcomes implies the existence of consistent joint probabilities for the possible and actual outcomes of measurements such as![]() . Note, however, that these possible outcomes are now assumed to be listed in six-tuples with the setting-sequence of
. Note, however, that these possible outcomes are now assumed to be listed in six-tuples with the setting-sequence of ![]() on each island, in spite of the fact that actually only pairs are measured. From a set theoretic viewpoint we must ask ourselves: Which sets is Wigner discussing? Without doubt these must be sets of measurements of time-correlated pairs.
on each island, in spite of the fact that actually only pairs are measured. From a set theoretic viewpoint we must ask ourselves: Which sets is Wigner discussing? Without doubt these must be sets of measurements of time-correlated pairs.
As an aside, Bernard d’Espagnat [8] presented a counterfactual interpretation of Wigner’s work by introducing multiple hypothetical values that every single particle “possesses” and that are assumed to exist in addition to the possible measurement outcomes for particle pairs. We do not make these additional unwarranted assumptions. Our reasoning below does, however, also apply to d’Espagnat’s work, with the addition of our findings about counterfactual approaches in [7] .
Wigner himself intended, as did Bell originally, to use exclusively elements of physical reality in the sense of Mach and we discuss his work from this point of view only.
4. Problems with Wigner’s Set-Theoretical Assumptions
As an illustration of how far reaching Wigner’s assumptions are, consider Bell’s six-tuple (2) which contains three correlated pairs and add to each of the pairs an arbitrary (artificial) third notebook entry for the setting that is not already contained in the pair-outcomes: setting ![]() for the first pair,
for the first pair, ![]() for the second and
for the second and ![]() for the third. As an example we obtain then for the first pair-column a triple-column:4
for the third. As an example we obtain then for the first pair-column a triple-column:4
![]() (4)
(4)
The ![]() as subscripts indicate the arbitrariness of choice of the additions. We have separated these additions by “
as subscripts indicate the arbitrariness of choice of the additions. We have separated these additions by “![]() ” instead of “
” instead of “![]() ”, because the latter indicates the separation of the measurements on two islands and it is not determined from which island the additions originate. The three entries are also not all correlated in time, because
”, because the latter indicates the separation of the measurements on two islands and it is not determined from which island the additions originate. The three entries are also not all correlated in time, because ![]() cannot equal any of the other measurement times of the triple. Different settings must correspond to different times in Einstein’s physics. We did not use the symbol
cannot equal any of the other measurement times of the triple. Different settings must correspond to different times in Einstein’s physics. We did not use the symbol ![]() on the right side of (4) but used instead
on the right side of (4) but used instead![]() , because the pairing by mea- surement times cannot be guaranteed for all of them. Together with the other two pairs of the Bell six-tuple, we obtain thus three triples each with settings
, because the pairing by mea- surement times cannot be guaranteed for all of them. Together with the other two pairs of the Bell six-tuple, we obtain thus three triples each with settings![]() . All the followers of Bell and Wigner, not just d’Espagnat but also Leggett-Garg [19] and others, assume explicitly or implicitly that the joint triple probabilities exist and are common to all three triples.
. All the followers of Bell and Wigner, not just d’Espagnat but also Leggett-Garg [19] and others, assume explicitly or implicitly that the joint triple probabilities exist and are common to all three triples.
However, it is a well known fact of probability theory, particularly the set theoretic probability theory of Kolmogorov, that the existence of joint triple (and higher order) probabilities is not guaranteed [4] , [13] . In the above example, each column of triples may, for example, have different joint triple probabilities and a joint triple probability that is common to all three columns of triples may not exist. The proof of the validity of Bell type inequalities requires an existence proof of joint triple (quadruple etc.) pro- babilities from the underlying physics. Wigner just assumed these probabilities to exist and, therefore, assumed what he had to prove.
This is an enormously important point that has been overlooked also by Bell and all his followers [2] . If one claims that Wigner’s approach is a set theoretic approach, we need to use a set theoretic definition of probability measures. Such a definition indeed exists and is, as mentioned, given by the probability framework of Kolmogorov [20] . That framework teaches us that, for a countable number of considered possible out- comes such as![]() , one can define consistent joint probabilities if and only if the actual measurements can also be listed or taken in form of such six-tuples so that we can establish a one to one correlation of any of Wigner’s
, one can define consistent joint probabilities if and only if the actual measurements can also be listed or taken in form of such six-tuples so that we can establish a one to one correlation of any of Wigner’s ![]() with the (possible) measurement outcomes
with the (possible) measurement outcomes ![]() and
and![]() . Wigner has thus made a mathematical assumption of serious consequences without having any physical or mathematical reason.
. Wigner has thus made a mathematical assumption of serious consequences without having any physical or mathematical reason.
Several different cases need to be considered to present the full proof that Wigner’s approach must not be applied to EPRB experiments. We just present one example that is typical and list the following six-tuple using Wigner’s subsets related to settings ![]() for both Tenerife and La Palma with a possible choice of measurement times included:
for both Tenerife and La Palma with a possible choice of measurement times included:
![]() (5)
(5)
The symbol “![]() ” separates the three Wigner subsets on one given island. The indexes
” separates the three Wigner subsets on one given island. The indexes![]() , represent natural numbers
, represent natural numbers ![]() that are now different from those used previously
that are now different from those used previously ![]() in the six-tuple (2). The reason for using a different notation is that six-tuples (2) and (5) cannot be transformed into each other without violating the space and time correlations of the actual pairing arising from the original measure- ments. The particular chosen pairing of six-tuple (5) is determined by the measurement times and thus is given by
in the six-tuple (2). The reason for using a different notation is that six-tuples (2) and (5) cannot be transformed into each other without violating the space and time correlations of the actual pairing arising from the original measure- ments. The particular chosen pairing of six-tuple (5) is determined by the measurement times and thus is given by![]() ,
, ![]() and
and![]() , while the pairing of six-tuple (2) is
, while the pairing of six-tuple (2) is![]() ,
, ![]() and
and ![]() and the pairing by measurement times must be different whenever the topology (location and setting) of the measurements of the pairs is different.
and the pairing by measurement times must be different whenever the topology (location and setting) of the measurements of the pairs is different.
Wigner never included considerations of both measurement times and topology and used six-tuple (5) to obtain the possible outcomes for all the following 9 possible pairings:
![]() (6)
(6)
We use again ![]() only for the guaranteed correlated pairs (through measurement times). For all other pairs we use
only for the guaranteed correlated pairs (through measurement times). For all other pairs we use![]() . For the pairings of Bell’s six-tuple (2) and using (3) Wigner thus obtains:
. For the pairings of Bell’s six-tuple (2) and using (3) Wigner thus obtains:
![]() (7)
(7)
The ![]() and
and ![]() denote here a certain given outcome of either
denote here a certain given outcome of either ![]() or
or![]() . For example, we may have
. For example, we may have![]() ,
, ![]() ,
, ![]() and
and![]() . This innocently look- ing fact represents a big restriction for the possible outcomes. The two pairs with settings
. This innocently look- ing fact represents a big restriction for the possible outcomes. The two pairs with settings ![]() and
and ![]() must now have the same outcome
must now have the same outcome ![]() in Tenerife and the same is true for the two pairs
in Tenerife and the same is true for the two pairs ![]() and
and ![]() which now must have identical outcome
which now must have identical outcome ![]() in La Palma in spite of the fact that they must, in principle, corres- pond to two different pairs of actual measurement.
in La Palma in spite of the fact that they must, in principle, corres- pond to two different pairs of actual measurement.
We consider now the possible correlations for the outcomes of the ![]() six-tuples of Bell (corresponding to
six-tuples of Bell (corresponding to ![]() measurements of pairs) that lead to different ratios of equal and different outcomes of the pairs. The number of these correlations is reduced from the original
measurements of pairs) that lead to different ratios of equal and different outcomes of the pairs. The number of these correlations is reduced from the original ![]() to only
to only ![]() different possibilities of correlations as can be seen from six-tuple (7). If we also require that
different possibilities of correlations as can be seen from six-tuple (7). If we also require that ![]() as Wigner did, because he argued that equal settings need to have equal outcomes, then we obtain only
as Wigner did, because he argued that equal settings need to have equal outcomes, then we obtain only ![]() different possibilities of correlating equal
different possibilities of correlating equal ![]() and different
and different ![]() outcomes for the pairs in Bell’s six-tuples (2). This latter reduction is identical to the reduction obtained by Bell in his inequality.
outcomes for the pairs in Bell’s six-tuples (2). This latter reduction is identical to the reduction obtained by Bell in his inequality.
As seen from the measurement times, only 3 of the pairings of (6) do correspond to originally correlated pairs. Note that ![]() and
and ![]() cannot be treated on the same footing, although they have only interchanged settings. It is also very important to note that only one pair of Wigner’s (7) is actually correlated. Each of the equal settings chosen on the same island must appear with different measurement time in Bell’s six- tuple (2). In contrast, any setting that appears twice on the same island must be asso- ciated with the same measurement and, therefore, be related to the same measurement time because of Wigner’s procedure involving six-tuple (5). However, it is physically impossible to actually measure two different pairs which exhibit the same setting and the same measurement time at one given location.
cannot be treated on the same footing, although they have only interchanged settings. It is also very important to note that only one pair of Wigner’s (7) is actually correlated. Each of the equal settings chosen on the same island must appear with different measurement time in Bell’s six- tuple (2). In contrast, any setting that appears twice on the same island must be asso- ciated with the same measurement and, therefore, be related to the same measurement time because of Wigner’s procedure involving six-tuple (5). However, it is physically impossible to actually measure two different pairs which exhibit the same setting and the same measurement time at one given location.
Thus, Wigner reduced the number of possible correlations of EPRB measurements by assuming without justification the existence of certain joint probabilities. He did not realize this fact and was, therefore, faced with the problem to explain the contradictions with actual experiments if they occurred (and as indeed were found [10] [11] [14] [15] [16] . Because Wigner was convinced that he used only set theory and Einstein’s local realism, he mentioned that a violation of Einstein’s separation principle would lead to “![]() domains ・・・ of the nine measurements” corresponding to Equation (6). He thus introduced violations of Einstein’s realism to explain possible future disagreements of his theory with experiments and measurements, so to speak as a deus ex machina, that would resolve contradictions; not as essential part of his proof.
domains ・・・ of the nine measurements” corresponding to Equation (6). He thus introduced violations of Einstein’s realism to explain possible future disagreements of his theory with experiments and measurements, so to speak as a deus ex machina, that would resolve contradictions; not as essential part of his proof.
We note in passing that all of our (and Wigner’s) reasoning that is related to the triple of settings ![]() and Bell’s inequality can be repeated with the same findings for quadruples
and Bell’s inequality can be repeated with the same findings for quadruples ![]() and the CHSH inequality.
and the CHSH inequality.
5. Conclusion
These facts show that Wigner’s procedure to derive Bell’s inequality is set-theoretically neither general nor sound. Wigner’s work, taken in conjunction with experiments such as presented in [10] [11] [14] [15] [16] does not prove violations of Einstein’s realism. It proves only that Wigner’s assumptions about the existence of certain joint probabili- ties are incorrect. As discussed above, the essential part of Wigner’s proof does not use Einstein’s local realism at all. Thus, we believe to have shown beyond any reasonable doubt that Wigner derived his reduction of possible correlations and his Bell type inequality from set theoretically unjustified assumptions about the existence of joint probabilities.
NOTES
![]()
1We do not wish to use quantum-physics arguments in our reasoning. However, it must be said that the nature of the experiments and the possibility of quantum fluctuations excludes any other method of pairing and leaves only space and time measurements. Suppose, for example, that we just count on each island the number of measurements and then assume that those with equal number (deduced from the counting) will be selected as correlated pairs (post measurement, of course). Then a single counting error (caused for example by a quantum fluctuation in the measurement equipment) will completely mess up the ordering and will lead to pairing of the wrong entities. One must, therefore, use synchronized clocks in the space-like separated measurement stations, as well as knowledge about the space-like separation in order to identify which detector clicks represent, with high likelihood, measurements of a correlated pair.
![]()
3The Bell’s reasoning starts to deviate here from Wigner because of his introduction of counterfactually definite functions. We have dealt with this approach in connection with a many body dynamics of particle-equipment interactions in [7] .
2The mathematical proof for this fact is easily performed by writing out the possible different outcomes in matrix-form (first column all equal, last all different) and using the method of complete induction assuming correctness for ![]() and proving the result for
and proving the result for![]() . We have previously given a very transparent proof by using the numbers
. We have previously given a very transparent proof by using the numbers ![]() and
and ![]() for the possible equal and different pair-outcomes respectively [8] .
for the possible equal and different pair-outcomes respectively [8] .
![]()
4This is precisely what d’Espagnat did in his variation on the theme of Wigner (see p162 of his essay in Scientific American [8] ).