Piketty’s Inequality between the Profit and Growth Rates and Its Implications for the Reproduction of Economic Elites ()
1. Introduction
One of the salient features of a modern economy, as demonstrated by Piketty ( [1] , pp. 350-358), is that, as a general rule, the profit rate 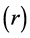 is higher than the growth rate
is higher than the growth rate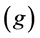 . This may not be the case for a given country during long periods of time but it is still possible that some capital investments get a profit rate greater than the growth rate of the country in one such period. As the gap between the two rates becomes greater for a particular investment, the opportunity increases for the investor to enlarge his personal fraction of the country’s capital stock. Furthermore, Piketty ( [1] , pp. 271-303) showed that, in higher income strata, income consists mostly of profits and also that greater capital investments tend to obtain higher profit rates (Piketty [1] , pp. 430-467). These combined facts produce a tendency for income to concentrate at the higher strata. To emphasize its importance, Piketty ( [1] , pp. 25-27) presents the inequality
. This may not be the case for a given country during long periods of time but it is still possible that some capital investments get a profit rate greater than the growth rate of the country in one such period. As the gap between the two rates becomes greater for a particular investment, the opportunity increases for the investor to enlarge his personal fraction of the country’s capital stock. Furthermore, Piketty ( [1] , pp. 271-303) showed that, in higher income strata, income consists mostly of profits and also that greater capital investments tend to obtain higher profit rates (Piketty [1] , pp. 430-467). These combined facts produce a tendency for income to concentrate at the higher strata. To emphasize its importance, Piketty ( [1] , pp. 25-27) presents the inequality 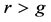 as the main cause of greater income inequality.
as the main cause of greater income inequality.
Building on the arguments offered by Piketty in favor of his thesis, this paper adds clarifications developed within the framework of the growth model introduced in Benítez [2] . In order to achieve this, the paper studies the differences between the economic growth rate and the growth rates of capital and of national income as functions of the capital/income ratio. Furthermore, the implications of these differences for the concentration of income are analyzed. Although Piketty’s book has been discussed in a great number of publications, these topics have not been studied previously in the specialized literature, as far as I know.
There are two contributions of this paper that may be of particular importance. The first is that it shows the key part played by the capital and national income growth rates for the concentration of income when the two rates are formulated as functions of the capital/income ratio and the economic growth rate. This brings a slightly different perspective to the analysis developed in Piketty [1] where production is defined in net terms so that the production and income growth rates are the same. The second one consists in the definition of three types of renters and of sufficient conditions for the existence of each one of them, which points out some qualitative differences between economic dynasties.
Regarding the first contribution, two conclusions relating some of the main variables of the model are particularly salient. First, the national income growth rate is greater than, equal to or less than the economic growth rate if the capital/income ratio respectively, decreases, stays constant or increases between two successive production periods. Second, the economic growth rate is equal to the sum plus the product of the growth rates of employment and of the average productivity of labor. These specifications are important, on the one hand, because the first one helps to explain certain aspect of income concentration as function of the capital/income ratio, such as the extension and the intensity of concentration for a given level of the economic growth rate. On the other hand, they allow establishing that the concentration of income in the higher income strata is limited almost exclusively by variations of the capital/income ratio and of the average productivity of labor, while the employment growth rate plays only a secondary role.
Regarding the second contribution, the paper underscores the difference between the concentration of income in favor of the capital owners as a class and that which favors the groups of higher incomes, referred to in the paper as economic elites. It shows that each type of concentration may occur without the other which is relevant because their meaning can also be different. Indeed, due to the fact that each consumer may own a share of capital, the first type does not exclude that workers receive part of the profit and, for this reason, income inequality depends on the distribution of capital ownership among consumers. If this distribution is particularly unequal, the second type of concentration takes place, propitiating the existence of renters and also of dynasties of renters whose share in the ownership of the national capital stock increases with each generation, which constitutes a feudal-style development within capitalist societies.
In addition to this introduction, the text contains four sections. Section 2 presents the basic model of Sraffa [3] and the growth path studied here. Section 3 defines the variables relevant to this study and also goes into some of its properties. Section 4 introduces a model of Bank centralizing transactions among economic agents and also the definition of some related concepts. Section 5 studies the concentration of income both among individuals and among social strata as well. Section 6 studies three types of renters, and an overall view of the results of the study is resumed in the last section.
2. The Growth Model
In this section, I present the basic model of Sraffa and the growth path studied here.
2.1. Sraffa’s Basic Model
I consider a succession of annual production processes starting on dates 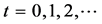 and, in order to identify each one of them, I refer to the date corresponding to the end of production. There are
and, in order to identify each one of them, I refer to the date corresponding to the end of production. There are 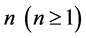 industries each one producing a particular type of good. To each good, and to the industry producing that good, corresponds an index
industries each one producing a particular type of good. To each good, and to the industry producing that good, corresponds an index 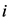 or
or 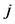 so that
so that  For each pair
For each pair 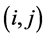 and for each
and for each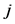 ,
, 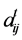 and
and 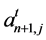 are respectively the quantities of
are respectively the quantities of 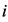 and of labor consumed directly in the production of one unit of
and of labor consumed directly in the production of one unit of 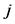 in period
in period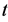 . I assume that
. I assume that 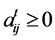 for every
for every  and
and 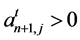 for every
for every![]() . For each
. For each![]() , the
, the ![]() matrix
matrix ![]() represents the means of production technical coefficients and its Frobenius root is
represents the means of production technical coefficients and its Frobenius root is![]() . Every good is basic which means that each good produces every good either directly or indirectly. This implies that
. Every good is basic which means that each good produces every good either directly or indirectly. This implies that ![]() is indecomposable and, for this reason,
is indecomposable and, for this reason,![]() . Furthermore, I assume that
. Furthermore, I assume that ![]() is viable (see Benítez [4] ), which means that:
is viable (see Benítez [4] ), which means that:
![]() . (1)
. (1)
For each couple ![]() and for each
and for each![]() ,
, ![]() and vector
and vector ![]() are respectively the price of good
are respectively the price of good ![]() and the price system of goods produced in period
and the price system of goods produced in period![]() . The wage unit
. The wage unit ![]() is paid at the end of production and the profit rate
is paid at the end of production and the profit rate ![]() is the same in all industries. In these conditions, the relation between the price and the cost of production of each good allows to formulate the following equation system:
is the same in all industries. In these conditions, the relation between the price and the cost of production of each good allows to formulate the following equation system:
![]() (2)
(2)
Making![]() , system (2) determines prices measured in wage units that correspond to each level of the rate of profit within an interval described in Section 3.2. Multiplying those prices by the wage measured with any given bundle of goods result in prices measured in that bundle as unit.
, system (2) determines prices measured in wage units that correspond to each level of the rate of profit within an interval described in Section 3.2. Multiplying those prices by the wage measured with any given bundle of goods result in prices measured in that bundle as unit.
It should be added that one of the constraints of the model presented here, the fact that includes only those goods that produce all the goods, may be overcome using the Leontief’s closed model once the adaptations required are introduced. Indeed, as Benítez [5] shows, that model allows representing an economy in which not all goods are basic using a model in which all are.
2.2. The Growth Path
For each couple![]() , the quantity of good
, the quantity of good ![]() produced in period
produced in period ![]() is
is ![]() and the vector
and the vector ![]() indicates the goods produced in the period. Due to the fact that matrix
indicates the goods produced in the period. Due to the fact that matrix ![]() is indecomposable, the equation system:
is indecomposable, the equation system:
![]() (3)
(3)
has a unique solution ![]() determined up to a scalar factor. This equation implies that, for each good, the ratio between the quantity used as input and the amount produced is equal to
determined up to a scalar factor. This equation implies that, for each good, the ratio between the quantity used as input and the amount produced is equal to![]() .
.
For![]() , the magnitude of vector
, the magnitude of vector ![]() is fixed by the equation:
is fixed by the equation:
![]() (4)
(4)
while, for ![]() that magnitude is fixed by the equation:
that magnitude is fixed by the equation:
![]() (5)
(5)
where, for each ![]()
![]() is the growth rate of the whole product, or economic growth rate, from period
is the growth rate of the whole product, or economic growth rate, from period ![]() to period
to period![]() , which is determined as indicated ahead in Section 3.5. It follows from Equation (5) that, for each pair
, which is determined as indicated ahead in Section 3.5. It follows from Equation (5) that, for each pair ![]() such that
such that![]() :
:
![]() (6)
(6)
and also that the vector of quantities produced in any given production cycle is a multiple of the vector produced in the first cycle.
Let ![]() and, for each
and, for each ![]() let:
let:
![]() (7)
(7)
It follows from Equation (7) that, for each ![]() such that
such that![]() :
:
![]() (8)
(8)
Using the notation just introduced it is possible to write Equation (5) as follows:
![]() (9)
(9)
On the other hand, for each![]() , the production program of period
, the production program of period ![]() is obtained by multiplying each equation
is obtained by multiplying each equation ![]() of system (2) by the corresponding coordinate
of system (2) by the corresponding coordinate![]() , resulting:
, resulting:
![]() (10)
(10)
Starting from the second year, each production process uses the same set of means of productions as the previous one plus the part of the net product of that process that was not consumed. For this to be possible, I assume that consumers save a fraction of the net product of each year and also that, for every pair![]() , the proportion between the means of production technical coefficients corresponding to two successive production periods is the same (see Benítez [2] ).
, the proportion between the means of production technical coefficients corresponding to two successive production periods is the same (see Benítez [2] ).
In each period ![]() the transactions take place on two different calendar dates. Those corresponding to the beginning of the production process are made in the afternoon of day
the transactions take place on two different calendar dates. Those corresponding to the beginning of the production process are made in the afternoon of day ![]() and those corresponding to its end are made in the morning of day
and those corresponding to its end are made in the morning of day ![]() as described ahead, in Section 4.1.
as described ahead, in Section 4.1.
3. Average Productivity of Labor, Profit and Growth Rates
In this section, I present the definitions and some properties of the main variables considered in this study.
3.1. Capital and National Income
It follows from Equation (3) that, for every![]() , it is possible to represent the set of goods used in production and the set of goods that constitute the net product respectively by vectors
, it is possible to represent the set of goods used in production and the set of goods that constitute the net product respectively by vectors ![]() and
and![]() . Thus, the capital
. Thus, the capital ![]() and the national income
and the national income ![]() of period
of period ![]() are determined by:
are determined by:
![]() (11)
(11)
and
![]() (12)
(12)
Then, the capital/income ratio of period ![]() is given by:
is given by:
![]() (13)
(13)
![]() (14)
(14)
Therefore, this ratio is independent of the distribution of income and depends only on the technique of the period considered.
Prices will be measured with the value of the whole product of the first period of production, which permits to relate some macroeconomic variables with the growth rates of the different production periods. Indeed, for every ![]() if prices are measured in period
if prices are measured in period ![]() with the whole product of the first period, then:
with the whole product of the first period, then:
![]() (15)
(15)
On the other hand, multiplying both sides of Equation (9) by ![]() yields:
yields:
![]() (16)
(16)
The last two equations imply that:
![]() (17)
(17)
This result and the definitions of capital and national income presented above imply respectively that:
![]() (18)
(18)
and
![]() (19)
(19)
Due to the fact that these formulas are independent of changes in relative prices taking place in the different production periods, they facilitate comparing capital and income pertaining to those periods, as shown in the next section.
3.2. Capital and Economic Growth Rates
Equation (18) for period ![]() is:
is:
![]() (20)
(20)
Dividing term by term Equation (18) by Equation (20), results in:
![]() (21)
(21)
Substituting ![]() in this equation by its equivalence according to Equation (8) gives:
in this equation by its equivalence according to Equation (8) gives:
![]() (22)
(22)
![]() (23)
(23)
Furthermore, Equation (14) implies that:
![]() (24)
(24)
![]() (25)
(25)
![]() (26)
(26)
Equation (26) corresponding to period ![]() is:
is:
![]() (27)
(27)
Dividing term by term Equation (27) by Equation (26) and simplifying results in:
![]() (28)
(28)
Equations ((23) and (28)) taken together imply that:
![]() (29)
(29)
For each ![]() let
let ![]() be the capital growth rate from period
be the capital growth rate from period ![]() to period
to period![]() . It follows from Equation (29) that:
. It follows from Equation (29) that:
![]() (30)
(30)
Thus, we can formulate the following conclusion:
Proposition 1. The capital growth rate from period ![]() to period t is greater than, equal to, or less than the economic growth rate if the capital/income ratio of period
is, respectively, greater than, equal to, or less than the capital/income ratio of period
to period t is greater than, equal to, or less than the economic growth rate if the capital/income ratio of period
is, respectively, greater than, equal to, or less than the capital/income ratio of period![]() .
.
The next example allows having an idea of the order of magnitude of the first factor between parentheses on the right hand side of Equation (30).
Example 1. According to Graphic 3.6 by Piketty ( [1] , p. 128) and Table S3.2 by Piketty [6] national capital measured by national income in France was equal to 2.78 in 1950 and, starting from this year increased coming to 6.05 en 2010. Thus, assuming a
constant increase, the average value of capital in that 60 years period was ![]() while the annual variation in the value of capital was
while the annual variation in the value of capital was![]() . Therefore, if
. Therefore, if ![]() is an average year
is an average year ![]() and
and![]() . Substituting
. Substituting ![]() and
and ![]() by their corresponding values in the first factor between parentheses on the right hand side of Equation (30) gives:
by their corresponding values in the first factor between parentheses on the right hand side of Equation (30) gives:
![]() (31)
(31)
Therefore, due to the increase in the capital/income ratio the capital growth rate exceeded the economic growth rate in a percentage equal to ![]() . Hence, the first rate was
. Hence, the first rate was ![]() greater than the second from one year to the following one.
greater than the second from one year to the following one.
3.3. National Income and Economic Growth Rates
Equation (19) for period ![]() is:
is:
![]() (32)
(32)
Dividing term by term Equation (19) by Equation (32), results in:
![]() (33)
(33)
Substituting ![]() in this equation by its equivalence according to Equation (8) gives:
in this equation by its equivalence according to Equation (8) gives:
![]() (34)
(34)
![]() (35)
(35)
Furthermore, Equation (14) implies that:
![]() (36)
(36)
![]() (37)
(37)
![]() (38)
(38)
Equation (38) corresponding to period ![]() is:
is:
![]() (39)
(39)
Dividing term by term Equation (39) by Equation (38) and simplifying, results in:
![]() (40)
(40)
Substituting the first factor in the right-hand side of Equation (35) by the left-hand side of Equation (40) gives:
![]() (41)
(41)
For each![]() , let
, let ![]() be the national income growth rate from period
be the national income growth rate from period ![]() to period
to period![]() . It follows from Equation (41) that:
. It follows from Equation (41) that:
![]() (42)
(42)
Thus, we can formulate the following conclusion:
Proposition 2. The national income growth rate from period ![]() to period
to period ![]() is greater than, equal to, or less than the economic growth rate if the capital/income ratio of period
is greater than, equal to, or less than the economic growth rate if the capital/income ratio of period ![]() is, respectively smaller than, equal to, or greater than the capital/income ratio of period
is, respectively smaller than, equal to, or greater than the capital/income ratio of period![]() .
.
Finally, Equations ((41) and (42)) taken together imply that:
![]() (43)
(43)
The next example allows having an idea of the order of magnitude of the first factor between parentheses on the right hand side of Equation (42).
Example 2. Substituting ![]() and
and ![]() by their corresponding values according to Example 1 in the first factor between parentheses on the right hand side of Equation (42) gives:
by their corresponding values according to Example 1 in the first factor between parentheses on the right hand side of Equation (42) gives:
![]() (44)
(44)
Therefore, due to the increase in the capital/income ratio the economic growth rate exceeded the national income growth rate in a percentage equal to
![]() Hence, the first rate was
Hence, the first rate was ![]() greater than the second from one year to the following one.
greater than the second from one year to the following one.
3.4. Profit Rate and the Wage Share
For every![]() , the national income of period
, the national income of period ![]() is divided between wages
is divided between wages ![]() and profits. This assumption, taken together with Equation (19), implies that the corresponding amounts are respectively equal to
and profits. This assumption, taken together with Equation (19), implies that the corresponding amounts are respectively equal to ![]() and
and![]() . In turn, the last result and Equation (18) taken together imply that the profit rate is determined by the equation:
. In turn, the last result and Equation (18) taken together imply that the profit rate is determined by the equation:
![]() (45)
(45)
![]() (46)
(46)
When ![]() the profit rate is zero, increases monotonously as
the profit rate is zero, increases monotonously as ![]() decreases, and reaches its maximum level
decreases, and reaches its maximum level ![]() when
when![]() , which is determined by the following equation:
, which is determined by the following equation:
![]() (47)
(47)
Equations ((46) and (47)) taken together imply that:
![]() (48)
(48)
According to this equation, the profit rate is equal to the maximum profit rate multiplied by the fraction of national income which corresponds to profits. It should be added that, for each ![]() there is a
there is a ![]() uniquely determined satisfying system (2). Similarly, for every
uniquely determined satisfying system (2). Similarly, for every ![]() there is a
there is a ![]() uniquely determined satisfying system (2) (see Benítez [7] ).
uniquely determined satisfying system (2) (see Benítez [7] ).
3.5. Average Productivity of Labor, Employment and Economic Growth Rates
According to system (10) for each![]() , the quantity of labor employed in period
, the quantity of labor employed in period ![]() is determined by:
is determined by:
![]() (49)
(49)
Equations ((17) and (49)) taken together imply that the average productivity of labor ![]() of period
of period ![]() is:
is:
![]() (50)
(50)
I assume that, for each![]() , the labor technical coefficients of two successive periods of production are related in the following way:
, the labor technical coefficients of two successive periods of production are related in the following way:
![]() (51)
(51)
where ![]() is a scalar greater than
is a scalar greater than![]() . Equations ((49) and (50)) corresponding to period
. Equations ((49) and (50)) corresponding to period ![]() are, respectively:
are, respectively:
![]() (52)
(52)
and
![]() (53)
(53)
Substituting ![]() in Equation (52) by the left-hand side of Equation (51), results in:
in Equation (52) by the left-hand side of Equation (51), results in:
![]() (54)
(54)
Now, substituting in Equation (53) ![]() by the right-hand side of Equation (54) results in:
by the right-hand side of Equation (54) results in:
![]() (55)
(55)
Þ ![]() (56)
(56)
Multiplying and dividing the right hand side of this equation by ![]() gives:
gives:
![]() (57)
(57)
![]() (58)
(58)
Now, substituting the numerator and the term between square brackets in the right-hand side of this equation by their respective equivalences in Equations ((6) and (8)) yields:
![]() (59)
(59)
Equations ((49), (50) and (59)) taken together imply that:
![]() (60)
(60)
This means that
is the rate of variation of the average productivity of labor from period ![]() to period
to period![]() . Furthermore, substituting in this equation
. Furthermore, substituting in this equation ![]() and
and ![]() respectively by the right-hand side of Equations ((50) and (53)) yields:
respectively by the right-hand side of Equations ((50) and (53)) yields:
![]() (61)
(61)
Þ ![]() (62)
(62)
For each ![]() let
let ![]() be the employment growth rate from period
be the employment growth rate from period ![]() to period
to period![]() . Therefore:
. Therefore:
![]() (63)
(63)
Equations ((8), (62) and (63)) imply that:
![]() (64)
(64)
Þ ![]() (65)
(65)
The preceding analysis enables us to draw the following conclusion.
Proposition 3. The economic growth rate is equal to the sum plus the product of the growth rates of employment and of the![]() .
.
3.6 The Wage Share as Function of the Capital/Income Ratio
Equations ((14) and (47)) taken together imply that:
![]() (66)
(66)
In turn, this result and Equation (48) imply that:
![]() (67)
(67)
Þ ![]() (68)
(68)
Þ ![]() (69)
(69)
Equation (69) corresponding to period ![]() is:
is:
![]() (70)
(70)
Dividing term by term Equation (69) by Equation (70) results in:
![]() (71)
(71)
Þ ![]() (72)
(72)
The preceding analysis enables us to draw the following conclusion.
Proposition 4. Given two successive periods of production, for each level of the profit rate common to both periods, the fraction of national income corresponding to wages in the first is greater than, equal to or less than that which corresponds to the second if the capital/income ratio of the first is, respectively, less than, equal to or greater than the second.
Due to the fact that the capital/income ratio and the average productivity of capital change in opposed sense (see Benítez [2] ) this proposition may be easily restated in terms of the second variable.
Example 3. It follows from Table S6.2 by Piketty [6] that the average pure rate of profit in the period 1950-2010 was![]() . Substituting the corresponding data in the first factor on the right-hand side of Equation (72) with this information and the data from Example 1 results in:
. Substituting the corresponding data in the first factor on the right-hand side of Equation (72) with this information and the data from Example 1 results in:
![]() (73)
(73)
Therefore, due to the increase in the capital/income ratio, the wage share decreased ![]() from one year to the following one.
from one year to the following one.
3.7. The Wage Unit as a Function of the Averages Productivities of Capital and Labor
For each![]() , the wage unit is determined by the following equation:
, the wage unit is determined by the following equation:
![]() (74)
(74)
To study the effects of changes in the average productivities of capital and labor on the wage unit, it is useful to substitute in Equation (74) variables![]() ,
, ![]() , and
, and ![]() by their respective equivalences according to Equations ((43), (63) and (72)) which results in:
by their respective equivalences according to Equations ((43), (63) and (72)) which results in:
![]() (75)
(75)
Equations ((42) and (64)) taken together imply that:
![]() (76)
(76)
Substituting the sum ![]() in Equation (75) by the right-hand side of this equation yields:
in Equation (75) by the right-hand side of this equation yields:
![]() (77)
(77)
![]() (78)
(78)
This result and Equation (74) corresponding to period ![]() taken together imply that:
taken together imply that:
![]() (79)
(79)
Therefore, the wage unit in period
will be greater than, equal to or less than in period ![]() if the product:
if the product:
![]() (80)
(80)
is respectively, greater than, equal to or less than one. If the capital/income ratio increases in the second period, the first two factors in the product (80) are less than one for each level of the profit rate common to periods ![]() and
and![]() . For this reason, the wage unit decreases, except in the case where:
. For this reason, the wage unit decreases, except in the case where:
![]() (81)
(81)
If, on the other hand, the capital/income ratio decreases, the first two factors of function (80) are greater than one for each level of the profit rate common to periods ![]() and
and![]() . For this reason, the wage unit increases, unless:
. For this reason, the wage unit increases, unless:
![]() (82)
(82)
The next example allows having an idea of the order of magnitude of product (80).
Example 4. According to Table S2.3 by Piketty [6] , the average annual increase of the productivity of labor in the period 1950-2012 in Western Europe was![]() . Substituting
. Substituting ![]() by this value in product (80) and also making there the corresponding substitution according to the data from examples 2 and 3, it is possible to write that product as follows:
by this value in product (80) and also making there the corresponding substitution according to the data from examples 2 and 3, it is possible to write that product as follows:
![]() (83)
(83)
![]() (84)
(84)
Thus, notwithstanding the decrease in the wage share, due to the increase of the average productivity of labor, the wage unit increased by ![]() from one year to the following one.
from one year to the following one.
4. Personal Shares of Capital, Income and Labor
In this section, I introduce a model of a Bank centralizing transactions among economic agents and also define some related concepts.
4.1. Economic Agents and the Bank
In every production period, there is a single company in each industrial branch, to which corresponds the index of the good produced in the branch. For each![]() , the set of consumers in period
, the set of consumers in period![]() , referred to as the cohort
, referred to as the cohort![]() , is made up as follows: if
, is made up as follows: if![]() , the consumers are those individuals who own capital and, if
, the consumers are those individuals who own capital and, if![]() , the consumers are those individuals who receive a salary, a profit, or both types of income on date
, the consumers are those individuals who receive a salary, a profit, or both types of income on date![]() . The number of consumers
. The number of consumers ![]() varies according to the period in question, and to each consumer corresponds a particular index
varies according to the period in question, and to each consumer corresponds a particular index![]() .
.
There is a Bank in which, at noon of the first date of each period, are found deposited all the goods of the economy, which belong entirely to the consumers. Each consumer ![]() and each enterprise
and each enterprise ![]() has an individual bank account in which are recorded the operations carried out on each date, the value of deposits are indicated with positive amounts and withdrawals with negative amounts. For each couple
has an individual bank account in which are recorded the operations carried out on each date, the value of deposits are indicated with positive amounts and withdrawals with negative amounts. For each couple ![]() and
and ![]() balances corresponding to the end of the day are, respectively,
balances corresponding to the end of the day are, respectively, ![]() and
and![]() .
.
In the evening of each date![]() , the Bank notes in each company’s account a debt equal to the amount of the investment that is required during period
, the Bank notes in each company’s account a debt equal to the amount of the investment that is required during period ![]() and withdraws from the account of every consumer, without incurring in negative balance, the value of the goods that he needs during the same period. When the Bank concludes these accounting operations, the economic agents remove from the Bank the corresponding goods. I assume that, at
and withdraws from the account of every consumer, without incurring in negative balance, the value of the goods that he needs during the same period. When the Bank concludes these accounting operations, the economic agents remove from the Bank the corresponding goods. I assume that, at![]() , deposits in consumers’ accounts are sufficient for this purpose and, in addition, that in each period the wage is sufficient for the enlarged reproduction of the labor force.
, deposits in consumers’ accounts are sufficient for this purpose and, in addition, that in each period the wage is sufficient for the enlarged reproduction of the labor force.
In the morning of each date![]() , each company deposits in the Bank all of its production of the period
, each company deposits in the Bank all of its production of the period ![]() paying the company’s debt, the interest thereof (which is equal to the profit of the company), and wages for the period ending. Then, the Bank withdraws from each company’s account the amount of the wage for the period
paying the company’s debt, the interest thereof (which is equal to the profit of the company), and wages for the period ending. Then, the Bank withdraws from each company’s account the amount of the wage for the period ![]() corresponding to each consumer
corresponding to each consumer ![]() and deposits it on his individual account. In addition, it deposits the interest earned by the consumer’s savings during the period ending, equal to
and deposits it on his individual account. In addition, it deposits the interest earned by the consumer’s savings during the period ending, equal to![]() , so each company’s account remains at zero.
, so each company’s account remains at zero.
On each date![]() , saving equals investment by which the following equation is satisfied:
, saving equals investment by which the following equation is satisfied:
![]() (85)
(85)
I will represent with ![]() the left-hand side of this equation, which is equal to the amount of capital invested on date
the left-hand side of this equation, which is equal to the amount of capital invested on date![]() .
.
4.2. Capital, Income, and Labor Shares
For each pair ![]() such that
such that![]() ,
, ![]() is the amount of work carried out by consumer
is the amount of work carried out by consumer ![]() during period
during period![]() . Therefore, the income of consumer
. Therefore, the income of consumer ![]() in period
in period ![]() is:
is:
![]() (86)
(86)
and the total income is:
![]() (87)
(87)
Thus, for each pair ![]() such that
such that![]() , the fractions of labor and income corresponding to consumer
, the fractions of labor and income corresponding to consumer ![]() on date
on date ![]() are, respectively:
are, respectively:
![]() (88)
(88)
![]() (89)
(89)
and, for each pair![]() , the fraction of capital corresponding to consumer
, the fraction of capital corresponding to consumer ![]() on date
on date ![]() is:
is:
![]() (90)
(90)
For each![]() , vectors
, vectors ![]() and
and ![]() represent, respectively, the distribution of labor and income among consumers while, for each
represent, respectively, the distribution of labor and income among consumers while, for each![]() , vector
, vector ![]() represents the distribution of capital. Each of these vectors belongs to the set:
represents the distribution of capital. Each of these vectors belongs to the set:
![]() (91)
(91)
Equation (86) allows us to show that, when there is an increase in the wage unit and a concomitant decrease of the profit rate, the income of those agents whose income depends to a greater extent on labor will increase and vice versa (see Equations (48) and (74)). Therefore, given the distribution of labor and capital among consumers, the income distribution will vary depending on the rate of profit, and for each level of the same, such distribution is determined unequivocally. There is therefore, for each![]() , the function
, the function ![]() associating to each pair of vectors
associating to each pair of vectors ![]() the vector
the vector ![]() corresponding to the given level of
corresponding to the given level of![]() . On the other hand, for each given distribution of income among consumers, there are several distributions of capital and labor such that, for the given level of the profit rate, the distribution of income among consumers is the same. For this reason, there is no inverse function
. On the other hand, for each given distribution of income among consumers, there are several distributions of capital and labor such that, for the given level of the profit rate, the distribution of income among consumers is the same. For this reason, there is no inverse function![]() .
.
4.3. Individual and Collective Propensity to Save
For each pair![]() ,
, ![]() and
and ![]() are, respectively, the propensity to consume and to save of consumer
are, respectively, the propensity to consume and to save of consumer ![]() on date
on date![]() , whereas
, whereas ![]() and
and ![]() are the propensities corresponding to the set of consumers. I assume that, for each pair
are the propensities corresponding to the set of consumers. I assume that, for each pair ![]() the following propositions are true:
the following propositions are true:
![]() (92)
(92)
![]() (93)
(93)
The propensity to save for the set of consumers is obtained dividing the sum of saving by the total income, resulting in:
![]() (94)
(94)
![]() (95)
(95)
![]() (96)
(96)
Substituting the second factor in the right-hand side of this equation by the left-hand side of Equation (89) yields:
![]() (97)
(97)
In this manner, the propensity to save of the economy is the sum of the individual propensities, each one weighted by the fraction of the national income belonging to the corresponding consumer.
Let ![]() and
and![]() . Equation (97), taken together with the following equation:
. Equation (97), taken together with the following equation:
![]() (98)
(98)
implies that, if the propensity to save is the same for all consumers, the collective propensity to save is equal to the propensity to save of each consumer. On the other hand, if![]() , in the sum on the right-hand side of Equation (97) at least one fraction
, in the sum on the right-hand side of Equation (97) at least one fraction ![]() is being multiplied by a propensity to save smaller than
is being multiplied by a propensity to save smaller than ![]() and, at least another fraction is being multiplied by a propensity to save greater than
and, at least another fraction is being multiplied by a propensity to save greater than![]() . This remark, taken together with Equation (98), implies that:
. This remark, taken together with Equation (98), implies that:
![]() (99)
(99)
4.4. Division of Profits and Wages between Consumption and Savings
Multiplying Equation (86) by ![]() and by
and by ![]() results, respectively:
results, respectively:
![]() (100)
(100)
![]() (101)
(101)
Adding the first term on the right-hand side from the ![]() equations of type (100) and dividing the result by the sum of the wages we get the fraction of wages destined to consumption, represented with
equations of type (100) and dividing the result by the sum of the wages we get the fraction of wages destined to consumption, represented with![]() . Proceeding in analog form, results in
. Proceeding in analog form, results in![]() ,
, ![]() and
and![]() , which represent the fractions of saving on wages, of consumption on profits, and of savings on profits. It is useful to compare the amounts of profit and savings by means of the following function:
, which represent the fractions of saving on wages, of consumption on profits, and of savings on profits. It is useful to compare the amounts of profit and savings by means of the following function:
![]() (102)
(102)
Substituting the first term of this function by the sum ![]() and, the second term by the sum
and, the second term by the sum ![]() yields:
yields:
![]() (103)
(103)
Hence:
![]() (104)
(104)
In this way, the difference between profit and savings is equal to the difference between the amount of profits destined to consumption and the amount of wages destined to savings. This result and Proposition 1 of Benítez [2] allow drawing the following conclusions.
Proposition 5. Given two successive production periods, the profit rate of the first period is greater than, equal to, or less than the capital growth rate of the second if in the first period the amount of profit destined to consumption is, respectively, greater than, equal to, or less than the amount of wages destined to savings.
5. Personal and Strata Income Concentration
In this section, I establish some conditions for the concentration of income to take place both among individuals and among social strata as well.
5.1. Personal Income Share
For each![]() , when passing from date
, when passing from date ![]() to date
to date![]() , for each
, for each![]() , it follows from Equation (86) that the increase in the income of consumer
, it follows from Equation (86) that the increase in the income of consumer ![]() is determined by:
is determined by:
![]() (105)
(105)
![]() (106)
(106)
The wage part of a consumer income can vary from a period to the next by a change in the amount of work done, a change in the wage unit, or both. However, I assume that for each couple![]() :
:
![]() (107)
(107)
This is justified by the simplification introduced in the analysis and, additionally, by the following reasons. On the one hand, the average amount of work performed by an employee under normal circumstances varies little from a period to the next, and the variation in salary must also be small since, as I will suppose from now on, the profit rate is the same in periods ![]() and
and ![]() (see Example 2). Accordingly, the amount of the variation in wage income typically represents a small percentage of this income. On the other hand, the same amount should represent a smaller fraction of the change in the total consumer income as higher levels of income are considered. Indeed, as already indicated Piketty ( [1] , pp. 271-303) shows that, contrarily to what happens in other income strata, personal incomes consisting mainly of profits are predominant among the higher strata, and are precisely those income levels which I want to specifically study in this article.
(see Example 2). Accordingly, the amount of the variation in wage income typically represents a small percentage of this income. On the other hand, the same amount should represent a smaller fraction of the change in the total consumer income as higher levels of income are considered. Indeed, as already indicated Piketty ( [1] , pp. 271-303) shows that, contrarily to what happens in other income strata, personal incomes consisting mainly of profits are predominant among the higher strata, and are precisely those income levels which I want to specifically study in this article.
Thus, making![]() , it is possible to write:
, it is possible to write:
![]() (108)
(108)
Now, the difference between ![]() and
and ![]() is equal to the savings made by consumer
is equal to the savings made by consumer ![]() on date
on date![]() . Hence,
. Hence,
![]() (109)
(109)
Equations ((108) and (109)) taken together imply that:
![]() (110)
(110)
Therefore:
![]() (111)
(111)
5.2. Income Concentration within a Cohort
In this section, I study the concentration of income within a given cohort ![]() with a focus on the passage from date
with a focus on the passage from date ![]() to date
to date![]() . For simplicity, I assume that, on date
. For simplicity, I assume that, on date![]() , the first
, the first ![]() indexes correspond to consumers belonging to the cohort
indexes correspond to consumers belonging to the cohort![]() . For each
, let:
. For each
, let:
![]() (112)
(112)
The sum ![]() is the income of the cohort
is the income of the cohort ![]() on date
on date![]() . I assume that, on each date
. I assume that, on each date ![]() new consumers arrive. Thus:
new consumers arrive. Thus:
![]() (113)
(113)
It is important to note that assuming that the first ![]() indexes of cohort
indexes of cohort ![]() correspond to the consumers already present in cohort
correspond to the consumers already present in cohort ![]() implies that no inheritance takes place with the passage from one date to the following one, a topic studied ahead in Section 6. Because the new consumers lack capital on date
implies that no inheritance takes place with the passage from one date to the following one, a topic studied ahead in Section 6. Because the new consumers lack capital on date ![]() their income equals their salary on date
their income equals their salary on date![]() . This allows writing the above equation in the following form:
. This allows writing the above equation in the following form:
![]() (114)
(114)
On the other hand, for each ![]() belonging to cohort
belonging to cohort![]() , let:
, let:
![]() (115)
(115)
This fraction indicates the part of the income of cohort ![]() that corresponds to consumer
that corresponds to consumer ![]() on date
on date![]() . On the other hand, Equation (111) implies that:
. On the other hand, Equation (111) implies that:
![]() (116)
(116)
Substituting ![]() and
and ![]() in the right-hand side of Equation (115) by the right-hand side of, respectively, Equations ((111) and (116)) yields:
in the right-hand side of Equation (115) by the right-hand side of, respectively, Equations ((111) and (116)) yields:
![]() (117)
(117)
![]() (118)
(118)
![]() (119)
(119)
Replacing the first factor on the right-hand side of the last equation with its equivalent in accordance with definition (89) gives:
![]() (120)
(120)
Dividing by ![]() each term of the second factor in the right-hand side of this equation gives:
each term of the second factor in the right-hand side of this equation gives:
![]() (121)
(121)
which leads to the following conclusion.
Proposition 6. The fraction of the income of cohort ![]() that corresponds to a consumer
that corresponds to a consumer ![]() grows, remains constant or decreases from date
grows, remains constant or decreases from date ![]() to date
to date ![]() if, respectively, his propensity to save in
if, respectively, his propensity to save in ![]() is greater than, equal to, or less than the propensity to save of the entire economy.
is greater than, equal to, or less than the propensity to save of the entire economy.
I will say that a concentration of income takes place within a cohort from date ![]() to date
if the inequality
to date
if the inequality ![]() is satisfied for at least one consumer
is satisfied for at least one consumer![]() . It is worth adding that Proposition 6 and condition (99) taken together imply that such concentration occurs whenever the propensity to save is not the same for all consumers.
. It is worth adding that Proposition 6 and condition (99) taken together imply that such concentration occurs whenever the propensity to save is not the same for all consumers.
5.3. Income Concentration within Two Successive Cohorts
Dividing term by term Equation (111) by Equation (43) results in:
![]() (122)
(122)
Substituting the left-hand side of this equation by its equivalence in Equation (89) and simplifying the numerator on the right-hand side, we can write this equation in the following form:
![]() (123)
(123)
![]() (124)
(124)
In this way, replacing the first factor on the right-hand side of the last equation with its equivalent according to Equation (89) gets:
![]() (125)
(125)
This result allows drawing the following conclusion.
Proposition 7. For each![]() , the fraction of income that corresponds to the consumer
, the fraction of income that corresponds to the consumer ![]() grows, remains constant or decreases from date
grows, remains constant or decreases from date ![]() to date
to date ![]() if, respectively, the propensity to save of
if, respectively, the propensity to save of ![]() in
in ![]() weighted by the profit rate is greater than, equal to, or less than the national income growth rate.
weighted by the profit rate is greater than, equal to, or less than the national income growth rate.
I will say that a concentration of income takes place within two successive cohorts from date ![]() to date
to date ![]() if
if ![]() for at least one consumer
for at least one consumer![]() . It should be noted that, given the national income growth rate, whatever the propensities to save are for the different consumers, the profit rate can be sufficiently low, or, equivalently, the wage share can be sufficiently high, for all fractions of income to decrease.
. It should be noted that, given the national income growth rate, whatever the propensities to save are for the different consumers, the profit rate can be sufficiently low, or, equivalently, the wage share can be sufficiently high, for all fractions of income to decrease.
It follows from Equations ((89), (114) and (115)) taken together that every pair ![]() satisfies the relationship
satisfies the relationship![]() . In addition, the equality is true if and only if
. In addition, the equality is true if and only if![]() . In fact, as seen in Equation (114), when
. In fact, as seen in Equation (114), when ![]() tends to
tends to![]() , the income accounted for by those who are incorporated on date
, the income accounted for by those who are incorporated on date ![]() also tends to zero. In the limit, all income on date
also tends to zero. In the limit, all income on date ![]() is distributed among consumers belonging to cohort
is distributed among consumers belonging to cohort![]() .
.
5.4. Concentration of Income in Favor of a Population Stratum
Let ![]() and, given a particular value of
and, given a particular value of![]() , let
, let![]() . For each
. For each![]() ,
, ![]() represents the fraction of the national income that corresponds on date
represents the fraction of the national income that corresponds on date ![]() to the stratum
to the stratum ![]() of greater income, sorted by descending order. Notation
of greater income, sorted by descending order. Notation ![]() indicates the number of consumers who belong to the stratum
indicates the number of consumers who belong to the stratum ![]() and, for simplicity, I assume that the first
and, for simplicity, I assume that the first ![]() indexes correspond to these consumers. Normally, a part of consumers belonging to a stratum
indexes correspond to these consumers. Normally, a part of consumers belonging to a stratum ![]() on a given date are no longer there on the following date, either because of death or because they move to a different layer. However, to simplify, I will consider a stratum
on a given date are no longer there on the following date, either because of death or because they move to a different layer. However, to simplify, I will consider a stratum ![]() and assume that, given two successive dates, consumers belonging on the first date to stratum
and assume that, given two successive dates, consumers belonging on the first date to stratum ![]() are also part of it in the second. Consequently, it is possible to write:
are also part of it in the second. Consequently, it is possible to write:
![]() (126)
(126)
Let ![]() and
and ![]() be the average fractions of income in the sets of consumers included respectively in the first and second of these sums. With this notation, it is possible to write the above equation in the following form:
be the average fractions of income in the sets of consumers included respectively in the first and second of these sums. With this notation, it is possible to write the above equation in the following form:
![]() (127)
(127)
Since employment is growing at the rate![]() , the number of consumers in each stratum of income grows at that rate. For this reason,
, the number of consumers in each stratum of income grows at that rate. For this reason,![]() . On the other hand, I assume that consumers incorporated to the stratum
on the second date have an average income smaller than or equal to that of consumers already incorporated on
. On the other hand, I assume that consumers incorporated to the stratum
on the second date have an average income smaller than or equal to that of consumers already incorporated on
the earlier date, due to this![]() . Let
. Let![]() , this allows to write
, this allows to write ![]() Making appropriate substitutions, it is possible to write Equation (127) in the following way:
Making appropriate substitutions, it is possible to write Equation (127) in the following way:
![]() (128)
(128)
![]() (129)
(129)
On the other hand, replacing ![]() in the first sum of the right-hand side of Equation (126) by the right-hand side of Equation (125), it can be written as follows:
in the first sum of the right-hand side of Equation (126) by the right-hand side of Equation (125), it can be written as follows:
![]() (130)
(130)
The first term of the sum in parenthesis on the right-hand side of this equation is equal to![]() , the fraction of income accounted for by stratum
, the fraction of income accounted for by stratum ![]() on date
on date![]() , and the second, is the part of this fraction intended for saving weighted by the profit rate. In this manner, the propensity to save of stratum
on that date is given by the equation:
, and the second, is the part of this fraction intended for saving weighted by the profit rate. In this manner, the propensity to save of stratum
on that date is given by the equation:
![]() (131)
(131)
In accordance with the foregoing, it is possible to write the right-hand side of Equation (130) as follows:
![]() (132)
(132)
Substituting ![]() in Equation (129) by the formula (132) yields:
in Equation (129) by the formula (132) yields:
![]() (133)
(133)
Substituting now ![]() in Equation (133) by the right-hand side of Equation (76) results in:
in Equation (133) by the right-hand side of Equation (76) results in:
![]() (134)
(134)
![]() (135)
(135)
It should be noted that the second factor between square brackets on the right-hand side of this equation approaches one when the difference between the average earnings of the two groups of consumers, the one with ![]() and the one with
and the one with ![]() consumers approaches zero, as illustrated below.
consumers approaches zero, as illustrated below.
Example 5. If the average income of the consumer belonging to stratum b already on date ![]() is
is ![]() higher than that of the consumers arriving to stratum b on date
higher than that of the consumers arriving to stratum b on date![]() , then
, then![]() , thus
, thus![]() . If, in addition
. If, in addition![]() , the second factor between brackets on the right-hand side of Equation (135) is greater than or equal to
, the second factor between brackets on the right-hand side of Equation (135) is greater than or equal to![]() . Consequently, this factor reduces the magnitude of the product of the other two in less than 2 thousandths.
. Consequently, this factor reduces the magnitude of the product of the other two in less than 2 thousandths.
Therefore, if ![]() is sufficiently small, we can write:
is sufficiently small, we can write:
![]() (136)
(136)
Unlike what happens with the concentration of income in favor of individual consumers, the concentration of income in favor of a particular stratum ![]() is almost not affected by the employment growth. If the average productivities of labor and of capital are kept constant, the denominator of the factor between brackets in the last equation is equal to one. Therefore, given an absence of changes in productivity, the fraction of income of all those strata will increase where the value of
is almost not affected by the employment growth. If the average productivities of labor and of capital are kept constant, the denominator of the factor between brackets in the last equation is equal to one. Therefore, given an absence of changes in productivity, the fraction of income of all those strata will increase where the value of ![]() is sufficiently small, regardless of the size of the growth rate. It should be remembered that, due to condition (107) and some other hypothesis adopted, these conclusions represent better what happens in the higher income strata.
is sufficiently small, regardless of the size of the growth rate. It should be remembered that, due to condition (107) and some other hypothesis adopted, these conclusions represent better what happens in the higher income strata.
6. The Renters
In this section, I study the effect of saving on the existence of a class of renters under the assumption that the propensity to consume has the properties indicated by Keynes ( [8] , pp. 98-98). Thus, it is a continuous and monotonously decreasing function of income.
6.1. The Propensity to Save as an Increasing Function of Income
I assume that the per capita income ![]() of a reference production period
of a reference production period ![]() is sufficient to lead a comfortable life but does not allow one to make any savings, which occurs only from revenues exceeding
is sufficient to lead a comfortable life but does not allow one to make any savings, which occurs only from revenues exceeding![]() . Based on these conditions, I define next the propensity to save of each consumer.
. Based on these conditions, I define next the propensity to save of each consumer.
Hypothesis 1. There is a function ![]() that associates to each amount
that associates to each amount ![]() equal to or greater than
equal to or greater than ![]() the fraction of the same destined to saving. This function is continuous and monotonously increasing and, in addition
the fraction of the same destined to saving. This function is continuous and monotonously increasing and, in addition![]() .
.
It follows from the above that the inverse function exists ![]() which associates to each non-zero fraction aimed at savings the corresponding income. Based on the function
which associates to each non-zero fraction aimed at savings the corresponding income. Based on the function ![]() I define, for each pair
I define, for each pair![]() , the propensity to save of consumer
, the propensity to save of consumer ![]() on date
on date ![]() by means of the following two rules:
by means of the following two rules:
![]() (137)
(137)
![]() (138)
(138)
According to these rules, for each![]() , the fraction of income saved by consumer
, the fraction of income saved by consumer ![]() equals zero if his income is less than or equal to
equals zero if his income is less than or equal to![]() . If it is greater than
. If it is greater than![]() ,
, ![]() is a monotonous increasing function of
is a monotonous increasing function of![]() .
.
On the other hand, for each![]() , let
, let ![]() and
and ![]() . It follows from Hypothesis 1 and conditions ((137) and (138)) that, if the amount of income is the same for all the consumers, also the propensity to save is the same. Moreover, if
. It follows from Hypothesis 1 and conditions ((137) and (138)) that, if the amount of income is the same for all the consumers, also the propensity to save is the same. Moreover, if![]() , then
, then![]() , by which Equation (99) is fulfilled.
, by which Equation (99) is fulfilled.
6.2. Three Types of Renters
I call renter an individual who possesses a capital reporting a profit that allows him to live comfortably without having to participate in the production process. It should be added that this does not imply that the individual does not work but only that he has the possibility to refrain from working thanks to his share in the ownership of capital. It is useful to distinguish the following three types of renters.
Definition 1. A renter is a consumer who owns a capital reporting an annual profit equal to or greater than![]() .
.
Definition 2. A renter dynasty is a sequence of generations of a family lineage in which each member of the family belonging to these generations inherits a capital that, during the period between the granting of the heritage in two successive generations, increases enough so that the heirs of the following generation are also renters.
Definition 3. A quasi-feudal renter is a member of a dynasty of renters where each member bequeaths to each one of his descendants a fraction of the total capital that is at least equal to the one he himself received from his predecessors.
Now, I will proceed to calculate![]() ,
, ![]() and
and![]() , which are amounts of capital sufficient for their owners to belong, respectively, to each type of renter.
, which are amounts of capital sufficient for their owners to belong, respectively, to each type of renter.
A) Calculation of![]() . According to Definition 1:
. According to Definition 1:
![]() (139)
(139)
B) Calculation of![]() . I assume that each person retains his capital until the age of
. I assume that each person retains his capital until the age of ![]() years, when he distributes his assets among
years, when he distributes his assets among ![]() descendants whose average age is
descendants whose average age is
![]() years. These quantities are related as follows:
years. These quantities are related as follows:
![]() (140)
(140)
Then, to belong to a dynasty of renters, a consumer ![]() requires an inheritance
requires an inheritance ![]() received on date
that met the following condition:
received on date
that met the following condition:
![]() (141)
(141)
In order to simplify, I assume that the rate of saving is equal to ![]() in all the production periods considered in inequality (141). Then, it is possible to write it as follows:
in all the production periods considered in inequality (141). Then, it is possible to write it as follows:
![]() (142)
(142)
Þ ![]() (143)
(143)
Þ ![]() (144)
(144)
Conditions ((137) and (138)) taken together imply that:
![]() (145)
(145)
This result and inequality (144) taken together imply that there can be dynastic renters only if:
![]() (146)
(146)
Assuming that this inequality is met, the amounts of annual income satisfying condition (144) are characterized by the following inequality:
![]() (147)
(147)
Accordingly, to satisfy condition (141) it is enough for consumer ![]() to inherit the following amount of capital:
to inherit the following amount of capital:
![]() (148)
(148)
We thus reach the following conclusion. If inequality (146) is satisfied, then:
![]() (149)
(149)
The next example allows forming an idea of the order of magnitude of the variables considered.
Example 6. Let![]() ,
, ![]() ,
, ![]() and, for
and, for ![]() let:
let:
![]() (150)
(150)
Substituting the corresponding values in inequality (144) gives:
![]() (151)
(151)
Þ ![]() (152)
(152)
Therefore, to satisfy condition (141) it is enough owning a capital sufficiently large to live with ![]() or less of what is obtained as profit. Now, solving Equation (150) for
or less of what is obtained as profit. Now, solving Equation (150) for ![]() we get:
we get:
![]() (153)
(153)
Þ ![]() (154)
(154)
Þ ![]() (155)
(155)
Substituting in the right hand side of this equation ![]() by its minimum value according to inequality (152) gives:
by its minimum value according to inequality (152) gives:
![]() (156)
(156)
![]() (157)
(157)
![]() (158)
(158)
This equation indicates a sufficient annual income. The corresponding capital is:
![]() (159)
(159)
![]() (160)
(160)
Equations ((139) and (159)) taken together imply that![]() . In turn, this result, taken together with Equation (149), implies that:
. In turn, this result, taken together with Equation (149), implies that:
![]() (161)
(161)
Hence, in order to belong to a dynasty of renters it is enough to inherit the amount of capital just indicated.
C) Calculation of![]() . For a consumer
. For a consumer ![]() to be a quasi-feudal renter, the capital that he inherits at date
to be a quasi-feudal renter, the capital that he inherits at date ![]() must satisfy the following condition:
must satisfy the following condition:
![]() (162)
(162)
Þ ![]() (163)
(163)
To simplify, I assume that the propensity to save ![]() and the capital growth rate
and the capital growth rate ![]() are constant during the production periods considered in inequality (163). In this case, it is possible to write it as follows:
are constant during the production periods considered in inequality (163). In this case, it is possible to write it as follows:
![]() (164)
(164)
Þ ![]() (165)
(165)
Þ ![]() (166)
(166)
This condition and inequality (145) taken together imply that there can be quasi-feudal renters only if:
![]() (167)
(167)
On the other hand, according to condition (140) we have ![]() and, for this reason, inequality (167) implies that
and, for this reason, inequality (167) implies that![]() . The conclusion below follows from this result and Proposition 5.
. The conclusion below follows from this result and Proposition 5.
Proposition 8. If the rates of profit of capital growth and of individual savings are constant, there can be quasi-feudal renters only if the amount of profit destined to consumption is greater than the amount of wages destined to savings every year or the period considered.
Assuming that condition (167) is satisfied, it follows from inequality (166) that the next condition is also required:
![]() (168)
(168)
The amounts of annual income satisfying this condition are characterized by the following inequality:
![]() (169)
(169)
In order to satisfy this condition, it is enough for consumer ![]() to inherit the following amount of capital:
to inherit the following amount of capital:
![]() (170)
(170)
Thus, we reach the following conclusion. If inequality (167) is satisfied, then:
![]() (171)
(171)
Those that inherit an amount of capital equal to or greater than![]() , as well as their descendants, do not require to participate in the production process. In addition, the fraction of the total capital owned by each member of the dynasty is maintained constant or increases with each generation.
, as well as their descendants, do not require to participate in the production process. In addition, the fraction of the total capital owned by each member of the dynasty is maintained constant or increases with each generation.
The next example allows forming an idea of the order of magnitude of the variables considered.
Example 7. It follows from the data presented in Example 1 that, if the capital growth rate in the French economy had been constant during the period 1950-2010, the following equation must be satisfied:
![]() (172)
(172)
Þ ![]() (173)
(173)
![]() (174)
(174)
Substituting
in the right-hand side of inequality (167) by the right-hand side of Equation (174) and also substituting ![]() and
and ![]() with the data from Example 6 the right-hand side of inequality (167) can be written as follows:
with the data from Example 6 the right-hand side of inequality (167) can be written as follows:
![]() (175)
(175)
This result, taken together with the fact that the average annual profit rate in the French economy during the period considered was equal to ![]() (see Example 3), implies that the inequality (167) is satisfied. Now, substituting the corresponding data in the right-hand side of inequality (168) gives:
(see Example 3), implies that the inequality (167) is satisfied. Now, substituting the corresponding data in the right-hand side of inequality (168) gives:
![]() (176)
(176)
Þ ![]() (177)
(177)
Therefore, to satisfy condition (162) it is enough owning a capital sufficiently large to live with ![]() or less of what is obtained as profit. Now, substituting
or less of what is obtained as profit. Now, substituting ![]() in the right hand side of Equation (155) by its minimum value according to inequality (177) gives:
in the right hand side of Equation (155) by its minimum value according to inequality (177) gives:
![]() (178)
(178)
![]() (179)
(179)
![]() (180)
(180)
This equation indicates a sufficient annual income. The corresponding capital is:
![]() (181)
(181)
![]() (182)
(182)
Equations ((161) and (182)) taken together imply that![]() . In turn, this result and Equation (171) taken together imply that:
. In turn, this result and Equation (171) taken together imply that:
![]() (183)
(183)
Hence, in order to be a quasi-feudal renter it is enough to inherit the amount of capital just indicated.
It is worth mentioning that Condition (167) is not always met. However, in an economy where individual capitals obtain different profit rates, even if condition (167) is not satisfied by the average rate of profit of the economy it may be satisfied by the profit rate of some individual capitals
Furthermore, if the capital/income ratio decreases during the period considered, as occurred for instance in the French economy during the years 1910-1950 (see Benítez [2] , Example 1), then we have![]() . For this reason, conditions ((141) and (162)) taken together imply that in such a period every member of a renter dynasty is a quasi-feudal renter.
. For this reason, conditions ((141) and (162)) taken together imply that in such a period every member of a renter dynasty is a quasi-feudal renter.
The three categories of renters can include the same set of individuals although typically this does not happen. A renter may not be able to inherit to his descendants amounts of capital large enough for them to be also renters. A dynastic renter may belong to a renter dynasty where the proportion of total capital own by each of the members decreases from one generation to the following one. A quasi-feudal renter may lose his status either temporarily or definitely if changes in the profit rate of his individual capital stock, in the capital growth rate of the economy or in both variables are not favorable enough. For these reasons, the duration of a renter dynasty may vary widely.
6.3. Effects of Changes in the Capital/Income Ratio over Income Concentration
Substituting the sum ![]() in Equation (125) by the right-hand side of Equation (42) yields:
in Equation (125) by the right-hand side of Equation (42) yields:
![]() (184)
(184)
Regarding profits, we can infer from this equation two different effects on the concentration of income caused by an increase of the capital/income ratio while the other variables in the quotient between square brackets remain constant. The first one can be called extensive due to the growth of the percentage of the national capital stock whose profit is benefited by an increase with respect to the sum of income. Indeed, with the decrease in the national income growth rate, the participation in the total income increases not only for the individual profits that already did previously to this decrease, but also for the profits of some other capitals growing at smaller rates. The second can be called intensive because the individual profits that already increased their participation in the total income now grow in a proportion greater that before.
If instead, the capital/income ratio decreases, two effects take place opposed to those just mentioned. On the one hand, it diminishes the percentage of the national capital stock whose profit increases with respect to the national income. This is due to the fact that, because of the increase of the national income growth rate, some individual profits that previously grew or kept constant now decrease with respect to the national income. On the other hand, it reduces the rate of income concentration because profits that still increase their participation in the total income do it now in a smaller proportion than before.
Therefore, when the capital/income ratio varies, the increase in the capital share and the concentration of income in favor of the economic elites do not occur always together. It is important to note that the latter may occur both if this ratio increases as if it decreases, although both the extent and the intensity of the process of concentration are favored in the first case and decreased in the second. Furthermore, when the capital/income ratio increases, the growth rates of capital and of national income increase and decrease respectively. For these reasons, an increase of the capital/income ratio favors the formation of renter dynasties but hinders that of quasi-feudal dynasties and vice versa.
Finally, it is important to add that, while in the model studied here the profit rate is the same for all capitals, it follows from formula (125) that the concentration of income is an increasing function of the profit rate obtained by each individual capital. Hence, as already indicated, for that concentration to take place it is not required for the average profit rate of an economy to be higher than the growth rate of its national income. It is enough that one individual capital obtains a profit rate sufficiently greater than the mentioned growth rate.
7. Conclusions
Excluding the particular case in which all consumers receive an equal income, given a situation chosen randomly, in each cycle of production a concentration of income takes place within the corresponding cohort and, starting from a certain degree of inequality also is produced a concentration of income between two successive cohorts. This last development does not require for the average profit rate of an economy to be higher than the growth rate of its national income. It is enough that for at least one individual capital, the product of the corresponding profit and savings rates be above the national income growth rate, which tends to favor the growth of larger capitals given that they tend to get higher profit rates. Furthermore, consumers whose incomes are growing at a faster rate than the national income, also come to increase their propensity to save. Thus, in a succession of production periods there may be a persistent concentration of income in favor of the same consumers.
When capital property is sufficiently concentrated, some individuals can live comfortably without participating in the production process, their expenses being covered with their profits. A social class consisting of renters is thus formed and, within this, renter dynasties can be established. Moreover, some dynasties of particularly wealthy renters give a feudal bias to the development of capitalist societies since their participation in the ownership of the capital stock of the society increases with each generation.
It should be recalled that these conclusions refer to the particular model studied in this article, in which the forecasts of all agents are met, and therefore do not include the causes that can disrupt the uninterrupted growth of some individual capitals considered here. For this reason, they describe possible trends within capitalist economies whose presence in real economies must be verified in each case, which represents a considerable task for future research.
Acknowledgements
I am grateful to two anonymous referees for helpful comments and suggestions.