
1. Introduction
I reanalyze a model of quarks and leptons proposed in [1] [2] in order to find a guiding principle or cohesive symmetry to the model. The basic idea is to construct the quarks and leptons as three body bound states of two massless preons which have spin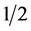 , charge
, charge 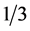 or 0. The preons form a three-member combinatorial system for the
or 0. The preons form a three-member combinatorial system for the 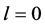 standard model (SM) fermions. From this basis, the color and weak interactions of particles can be deduced. When the energy or temperature is above the quark and lepton bound state ionization value strong and weak interactions drop out. Unification of interactions was suggested on preon level in [2] , with gravity and electromagnetism only contributing, but no unifying principle was introduced there. A method of unifi- cation by geometrization based on conformal symmetry is proposed in this note.
standard model (SM) fermions. From this basis, the color and weak interactions of particles can be deduced. When the energy or temperature is above the quark and lepton bound state ionization value strong and weak interactions drop out. Unification of interactions was suggested on preon level in [2] , with gravity and electromagnetism only contributing, but no unifying principle was introduced there. A method of unifi- cation by geometrization based on conformal symmetry is proposed in this note.
Conformal symmetry is introduced in the action using the Weyl tensor as described in [3] [4] . Gravity is quantized by coupling it to a quantized matter source [5] [6] . Electromagnetism is geometrized [7] to comport with gravity. A unitary, renorma- lizable quantum theory without ghosts is claimed. All symmetry breaking in the stan- dard model is dynamical, quantum mechanical due to fermion bilinear condensates in the vacuum. The resulting mass scale produces curvature or Schwarzschild radius. In the absence of quantum mechanics the geometry is flat.
Why endorse preons? There are a few reasons: 1) they open the possibility to reduce the number of basic constituents, 2) help to understand, or deduce, the standard model non-Abelian gauge interactions, 3) massless preons are natural basis for conformal symmetry which facilitates geometrical unification of desired interactions, and 4) massless preons offer possibilities to construct conformal models of cosmology without dark matter or energy [8] . Unfortunately, testing this preon model can be done at present on Gedanken experiment level only.
This paper is organized as follows. In Section 2, I discuss the preon model in some detail. In Section 3, following Mannheim, a brief review is given of conformal gravity, its local gauge and conformal invariance, and geometrization of electromagnetism. Conclusions are given in Section 4.
2. The Preon Model
The preon model described in [2] is based on a statistical black hole model in loop quantum gravity (LQG). In LQG the geometry is quantized such that the lowest area eigenvalue is zero, which allows zero mass particles in the model construction as the Brown-York energy is proportional to area. The idea that a particle can be defined in pure gravity theory was first put forward in [9] . There it was also found that a charged black hole with Reissner-Nordström metric can have zero mass.
In the present note I start from a different basis, namely conformal symmetry. The virtue of conformal symmetry is that the action for conformal gravity is defined uniquely by the Weyl tensor, described in subsection 3.1. All particles in conformal theory are massless1 Therefore in this note I assume zero mass preons on action level.
Requiring charge quantization  and preon permutation antisymmetry for identical preons, one can define three preon bound states which form the first generation quarks and leptons
and preon permutation antisymmetry for identical preons, one can define three preon bound states which form the first generation quarks and leptons
 (2.1)
(2.1)
The preons combine freely without other assumptions into standard model fermion bound states. They form a three member constrained combinatorial system. A binding interaction between preons is needed to make the quark and lepton bound states possible. I have at the moment no detailed form for this interaction. Its details are not expected to be of primary importance. I suppose this attractive, non-confining in- teraction is strong enough to keep together the charged preons but weak enough to liberate the preons at high temperature or after very long time period2. This interaction gives a small mass to quarks and leptons.
A useful feature in (2.1) with two identical preons3 is that the construction provides a three-valued subindex for quark SU(3) color, as it was originally discovered [10] . In addition, the weak SU(2) left handed doublets can be read from the first two and last two lines in (2.1). The SM gauge structure can be deduced in this sense from the present preon model. One could also have preon charges  and
and 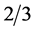 but then the index k distinction between quarks and leptons in (2.1) would be lost.
but then the index k distinction between quarks and leptons in (2.1) would be lost.
One may now propose that, as far as there is an ultimate unified theory, it is a preon theory with only gravitational and electromagnetic interactions operating between preons. The strong and weak forces are generated in the early universe later when massless preons combine into quarks and leptons at lower temperature and they operate only with short range interaction within nuclei making atoms, molecules and chemistry possible. In a contracting phase of the universe processes take place in the opposite order.
The unification picture is supposed to hold in the present scheme up to the energy of about 1016 GeV. The electroweak interaction has the spontaneously broken symmetry phase below an energy of the order of 100 GeV and symmetric phase above it. The electromagnetic and weak forces take separate ways at higher energies (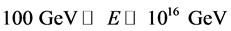 ), the latter melts away due to ionization of quarks and leptons into preons, but the former stays strong towards Planck scale,
), the latter melts away due to ionization of quarks and leptons into preons, but the former stays strong towards Planck scale,  . Likewise the quark color interaction suffers the same destiny as the weak force. One is left with the electromagnetic and gravitational forces only at Planck scale.
. Likewise the quark color interaction suffers the same destiny as the weak force. One is left with the electromagnetic and gravitational forces only at Planck scale.
Spin 3/2 quarks and leptons are implied by this model. States with higher number of preons are possible but will not be considered here.
The proton, neutron, electron and 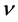 can be constructed of 12 preons and 12 anti- preons. The construction (2.1) is matter-antimatter symmetric on preon level, which is desirable for early cosmology. The model makes it possible to create from vacuum a universe with only matter: combine e.g. six
can be constructed of 12 preons and 12 anti- preons. The construction (2.1) is matter-antimatter symmetric on preon level, which is desirable for early cosmology. The model makes it possible to create from vacuum a universe with only matter: combine e.g. six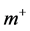 , six
, six 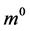 and their antiparticles to make the basic
and their antiparticles to make the basic  -decay particles. Corresponding antiparticles may occur equally well.
-decay particles. Corresponding antiparticles may occur equally well.
The baryon number (B) is not conserved [11] [12] in this model: a proton may decay at Planck scale temperature by a preon rearrangement process into a positron and a pion. This is expected to be independent of the details of the preon interaction. Baryon number minus lepton number (B-L) is conserved.
3. The Conformal Symmetry
3.1. Conformal Gravity
Weyl introduced, while working on the geometrization of electromagnetism, a new tensor called the Weyl or conformal tensor [13] (for an introduction to conformal theories, see e.g. [14] )
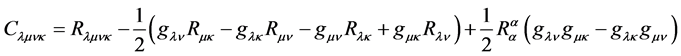 (3.1)
(3.1)
where  is the Riemann tensor. Under local conformal transformation
is the Riemann tensor. Under local conformal transformation  of the metric tensor
of the metric tensor  of the form
of the form
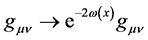 (3.2)
(3.2)
the Weyl tensor transforms correspondingly as
![]() (3.3)
(3.3)
The pure local conformal gravity is based on the following action
![]() (3.4)
(3.4)
where ![]() is a dimensionless gravitational coupling constant. Conformal gravity is power-counting renormalizable and unitary [4] . In
is a dimensionless gravitational coupling constant. Conformal gravity is power-counting renormalizable and unitary [4] . In ![]() there is no cosmological con- stant term since
there is no cosmological con- stant term since ![]() is not conformal invariant. The cosmological constant will appear later when conformal symmetry is dynamically broken and gives the dimensionful
is not conformal invariant. The cosmological constant will appear later when conformal symmetry is dynamically broken and gives the dimensionful ![]() a non-zero vacuum expectation value.
a non-zero vacuum expectation value.
The reason for local conformal invariance is that massless particles move on the light cone which is invariant under the 15 parameter conformal group SO(4,2) [6] . The covering group of ![]() (4,2) is SU(2,2). This is generated by the 15 Dirac matrices (
(4,2) is SU(2,2). This is generated by the 15 Dirac matrices (![]() ) and its fundamental representation is a fermionic field. There- fore it is natural to take fermions as the basic objects in physics. Gravity is generated by gauging the conformal symmetry of the light cone. Mass scales are to be generated dynamically by fermion bilinear condensates in the vacuum.
) and its fundamental representation is a fermionic field. There- fore it is natural to take fermions as the basic objects in physics. Gravity is generated by gauging the conformal symmetry of the light cone. Mass scales are to be generated dynamically by fermion bilinear condensates in the vacuum.
Functional variation of ![]() with respect to metric defines a gravitational rank two tensor
with respect to metric defines a gravitational rank two tensor ![]() in terms of the Riemann tensor that is covariantly conserved
in terms of the Riemann tensor that is covariantly conserved ![]() and traceless
and traceless![]() . Assuming a conformally invariant matter action
. Assuming a conformally invariant matter action ![]() (an example is discussed in the next subsection 3.2 variation with respect to
(an example is discussed in the next subsection 3.2 variation with respect to ![]() gives a fourth order derivative equation of motion of the form
gives a fourth order derivative equation of motion of the form
![]() (3.5)
(3.5)
By defining the left hand side of (3.5) as the energy-momentum tensor ![]() we can write (3.5) in the form
we can write (3.5) in the form
![]() (3.6)
(3.6)
We see that gravity and matter sectors are on equal footing and the total energy- momentum tensor of the universe is zero.
The connection between Einstein gravity and conformal gravity is that the solutions of the former are solutions of the latter [15] [16] . However, conformal gravity has more general solutions to be explored. From these the Einstein solutions can be chosen by imposing a certain Neumann boundary condition on the metric at the future boundary. The boundary condition eliminates ghosts and the theory becomes an Einstein theory with a cosmological constant.
3.2. Geometrization of Electromagnetism
Conformal invariance is also important for understanding the geometrization of other interactions. Metrication of electromagnetism coupled to a Dirac field is given in [7] .
The generalized Dirac action is
![]() (3.7)
(3.7)
where ![]() is a vierbein defined by
is a vierbein defined by ![]() (solving this for
(solving this for![]() , the vier- bein vectors are seen to diagonalize the metric tensor) and
, the vier- bein vectors are seen to diagonalize the metric tensor) and
![]() (3.8)
(3.8)
which is obtained from the generalized connection
![]() (3.9)
(3.9)
where ![]() and
and ![]() are the Levi-Civita and Weyl connections, respectively
are the Levi-Civita and Weyl connections, respectively
![]() (3.10)
(3.10)
![]() (3.11)
(3.11)
It turns out that the covariant derivative of the metric in (3.4) is non-zero, ![]() , and therefore parallel transport is path dependent and the theory is untenable.
, and therefore parallel transport is path dependent and the theory is untenable.
Secondly, in the Weyl connection drops out from the generalized Dirac action and therefore does not provide geometrization of electromagnetism. Replacing ![]() by
by
![]() (3.12)
(3.12)
and ![]() by
by ![]() in (3.4) one ends up with a satisfactory action
in (3.4) one ends up with a satisfactory action
![]() (3.13)
(3.13)
The action ![]() is locally invariant under both gauge and conformal transformations
is locally invariant under both gauge and conformal transformations ![]()
![]() (3.14)
(3.14)
One sees that ![]() does not transform at all. The equation of motion for preons, without preon-preon interactions, is (3.6).
does not transform at all. The equation of motion for preons, without preon-preon interactions, is (3.6).
4. Conclusions
The model proposed in this note makes an attempt to combine the phenomenological success of the standard model with one more fundamental layer of particles below the SM and apply the principle of conformal symmetry to the model. The preon layer allows one to deduce the non-Abelian interaction structure of the SM. Conformal symmetry is an important symmetry in gravity as well as in geometrization of other interactions, of which electromagnetism has a special role in the present scenario. The non-Abelian interactions of strong and weak forces are low energy short range in- teractions below the ionization energy of quarks and leptons. Open problems for future study include preon interactions and the three generations quarks and leptons. It has been my goal to explain the generations as preon level interactions but the fermion spectrum is too challenging. So far an elegant method for describing the three gene- rations may be the framed standard model [17] [18] .
In the models of quantum gravity mentioned above, LQG and conformal gravity, quantization takes place differently. LQG is a quantization approach for Hamiltonian formulation of pure Einstein gravity alone. The resulting geometry area and volume are quantized. Conformal gravity quantization is based on the quantized source of gravity. Electromagnetism can be metricated together with gravity. It remains to be seen which direction might be more fruitful in the future, both are geometric. Or will rather some- thing else be needed.
To close this note, I mention that in the search of detailed models for the present scenario, it seems that large scale modeling in cosmology is close to the idea of con- formal, or scale, symmetry as discussed extensively recently in [19] . Preons should be important in the very early and late phases of cosmological development. In the direction of Planck scale, or quantum gravity one may also have to consider models with deformation invariance more general than the conformal one [20] [21] . The meaning of preons is that they can give extra freedom in model building in various directions while keeping the number of basic interactions at two.
NOTES
![]()
1Conformal symmetry preserves angles, which guarantees the constancy of speed of light, i.e. the angle of light cone with respect to t-axis is 45 degrees. Mass can be generated to particles only dynamically. See subsection 3.1.
![]()
2Non-relativistically one may think of a potential wall or relativistically the SM vacuum energy is higher than the preon vacuum energy. As a first approximation this interaction can be introduced in flat spacetime.
3An assumption appears here that the same charge preons inside quarks have the same spin z-components.