The Effect of Laminate Angles in Composite Substrates on the Performance of Rectangular Microstrip Antenna ()
1. Introduction
Many studies of microstrip antenna design often assumed the substrate to be isotropic with uniform dielectric property. This “isotropic assumption” was made to conjecture the performance of a microstrip antenna attached on Kevlar composite substrate [1] and composite structure [2] . It has been known, however, that the resonant frequency of a microstrip antenna depends upon the substrate’s dimension (thickness) and material properties (permittivity and tangent loss). Yet little is known about the effects of composite substrate’s dielectric properties on antenna performance because of insufficient analytical models and/or numerical tools.
Composite laminated substrates have been widely used in aerospace structures, where continuous fiber/matrix layers stacking at suitable laminate angles can achieve desirable mechanical properties. Such substrates also facilitate embed- ding sensor/actuator and microstrip antenna to improve aerodynamic perfor- mance [3] . Previous studies of microstrip antenna in composite substrates were often by numerical methods, but none was able to predict the effects of different laminate angles on the substrate’s dielectric properties, and antenna performance.
The performance of a microstrip antenna attached on anisotropic layer is found to be strongly influenced by the substrate’s dielectric properties [4] [5] . A solution technique in frequency domain for analyzing electromagnetic wave propagation was developed to study an antenna embedded in composite laminated substrates [6] and to investigate the effect of dielectric overlay [7] . Recent study on microstrip antenna arrays on honey comb sandwich substrate [8] and composite laminated substrate [9] also validated that the antenna performance was sensitive to the substrate’s dielectric property―a function of the substrate’s laminate angles. Electromagnetic co-design by modeling the substrate structure is necessary [10] . Analytical solution would be desirable to conduct parametric study on substrate’s laminate angles affecting antenna performance.
2. Solution by Spectral Domain Analysis
Recent development of Conformal Load-bearing Antenna Structure (CLAS) by embedding microstrip antenna inside composite laminated substrates has been considered desirable. For a microstrip antenna with optical axis in y-direction on anisotropic substrate as illustrated in Figure 1, the permittivity matrix is
![]()
Figure 1. A microstrip antenna with its x-y-z axes of dimension (L ´ W) on the substrate with
1-2-3
axes in a laminate angle.
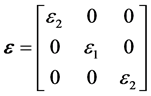(1)
with dielectric constant 
along the fiber direction and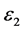 
along the other two normal axes, where
, 
, 
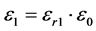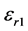and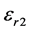 
are the relative
permittivity, and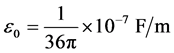 
in free-space. In isotropic substrates, the
optical axis (principal radiation direction) is normal to the antenna patch such that the permittivity matrix remains diagonal. In composite substrates, however, the antenna’s axes (x-y-z) may not necessarily be co-linear with any of the substrate’s principal axes (
1-2-3
). That leads to a non-diagonal permittivity matrix with 5 distinctive non-zero elements (permittivity), each being a function of the laminate angle θ. In spectral domain analysis [8] , the electromagnetic wave propagation of an antenna can be solved by using electric and magnetic Hertzian
potentials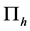 
and
. In vector form 
and
, where 
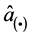is the unit vector of coordinate transformation between the antenna’s x-y-z and the substrate’s 1-2-3 axes. The wave equations in terms of the Fourier transform pairs 
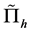and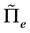 
can be written as
, (2a)
, (2b)
where![]()
, kx and kz are the Fourier variables of wave numbers with respect to x- and z-axis, respectively, ![]()
is the operating frequency,
![]()
and![]()
.
By the solution technique in spectral domain [4] , the electric and magnetic fields of a substrate (denoted by superscript s) are represented by the Hertzian potentials,
![]()
(3a)
![]()
(3b)
![]()
(
3c
)
and
![]()
(
4a
)
![]()
(4b)
![]()
(4c)
The Hertzian potentials are obtained by solving Equations 2(a) and 2(b)
![]()
, (
5a
)
![]()
. (5b)
Similarly the solutions in the air medium (with superscript a) are
![]()
(5c)
![]()
(5d)
where ![]()
and d is substrate thickness. The above coefficients![]()
, ![]()
, ![]()
, ![]()
, ![]()
and ![]()
are determined by the boundary conditions. At the interface of ground plane leads to![]()
, and the coefficients![]()
, ![]()
, ![]()
and ![]()
can be obtained by the 4 boundary equations in terms of the Hertzian potentials. Thus the tangential fields can be calculated by an algebraic equation of the immittance matrix and spectral current densities
![]()
(6)
The immittance matrix in Equation (6) is function of the laminate angle![]()
, substrate thickness d, dielectric constant ![]()
along the fiber direction and ![]()
along the other principal axes. Similar to previous work [4] , the spectral current densities can be solved by modal analysis. And the electromagnetic fields radiating in free space can then be determined by ![]()
and![]()
,
![]()
(7a)
![]()
(7b)
![]()
(7c)
The size, resonant frequency, and the radiation pattern of a microstrip antenna on substrates of different laminate angles can then be calculated.
3. Resonant Frequency by Modal Analysis
For a rectangular microstrip antenna of dimension L ´ W, the base functions in modal analysis for solving Equation (6) can be selected as
![]()
, (
8a
)
![]()
, (8b)
and in spectral domain they are
![]()
, (
8c
)
![]()
, (8d)
where ![]()
is the Dirac delta function. The antenna dimension can therefore be determined by the characteristic equation from Equation (6), and the electric field in space domain from Equations 7(a)-7(c) can be derived explicitly.
Consider the rectangular antenna from previous works [11] [12] : L =
1.0 cm
and W = 0.2 cm on a substrate ![]()
and thickness d = 0.158 cm to validate the modal analysis. Figure 2 shows the effect of substrate dielectric properties, represented by the substrate’s anisotropic ratio![]()
, on the resonant frequency at laminate angle![]()
. In the special case of isotropic substrate![]()
, ![]()
GHz agrees very well with that given by [11] . For anisotropic substrate, however, the resonant frequency is monotonically decreasing
![]()
Figure 2. Resonant frequency of a microstrip antenna (L = 1.0 cm and W = 0.2 cm) on substrates![]()
, ![]()
at different anisotropic ratios. Modal analysis results are validated by [11] on isotropic and by [12] on uniaxial substrates.
with increasing![]()
. ![]()
GHz when ![]()
while it is 4.9 GHz when![]()
. This result illustrates that the resonant frequency is strongly dependent on the substrate’s dielectric properties. In another special case, when![]()
, the substrate becomes uniaxial from mechanics view point, and the result also agrees very well with that in [12] . The resonant frequency remains monotonically decreasing at increasing![]()
. The above results show that the operating frequency of an antenna attached on isotropic, uniaxial or anisotropic substrate is significantly different because of the substrate’s permittivity. The frequency is in the range of 5 to 20 GHz depending on the substrate dielectric properties repre- sented by the anisotropic ratio.
In order to illustrate the effects of laminate angle on antenna performance, denote the size of a 2.4 GHz antenna on isotropic substrate by length ![]()
and width![]()
. Figure 3(a) shows the effects of anisotropic ratio and laminate angle on a 2.4 GHz antenna of patch size L ´ W. The anisotropic ratio is found to have little influence on patch size, ![]()
when![]()
; i.e., when![]()
, because the electromagnetic wave propagation is dominated by the dielectric properties along the laminate layer’s fiber direction. There are, however, large variations on antenna size, and similarly on resonant frequency, when ![]()
or![]()
.
In addition, the laminate angle has profound impact on the patch size of a 2.4 GHz antenna. For a given size of rectangular microstrip antenna, Figure 3(b) shows that the resonant frequency is dependent upon the laminate angle. At![]()
, the resonant frequency is at about 1.8, 1.3, and 2.4 GHz, respectively, for![]()
, 0.75, and 1.0. For the substrate of![]()
, the antenna frequency is about 1.4 GHz at laminate angle![]()
, while it is 1.3 GHz at ![]()
and 2.4 GHz at![]()
. Such significant differences in size and resonant frequency are critical to antenna design.
These results show that the laminate angle is critical to antenna performance. Electromagnetic wave propagation is very much influenced when![]()
, i.e.,![]()
. For all substrates with![]()
, the resonant frequency will deviate lower if mistakenly treating the substrate as isotropic. Antenna design without accounting for the substrate’s anisotropic nature of different ply angles can be erroneous.
4. Antenna Pattern by Modal Analysis
In addition to antenna size and resonant frequency, the effects of laminate angle on radiation pattern are even more sensitive. The far field patterns of an antenna operating at 2.4 GHz on y-z plane are shown in Figure 4. The radiation efficiency is scaled in the direction perpendicular to the microstrip patch, and the pattern of isotropic substrate (bold line) with the maxima in the normal direction is also plotted for reference. On composite substrates, however, the maxima will be shifted from the normal direction and is dependent on the laminate angle.
![]()
Figure 3. (a) The dimension of a 2.4 GHz microstrip antenna ![]()
and (b) the resonant frequency of a given size antenna on the substrates of different anisotropic ratios and laminate angles![]()
.
![]()
Figure 4. The far field patterns of a 2.4 GHz microstrip antenna on composite substrates (d = 1.00 cm) of anisotropic ratio (a) η = 0.50 and (b) η = 0.75 at different laminate angles![]()
.
In Figure 4(a), the E-field pattern on substrate with ![]()
and laminate angle ![]()
has more radiation intensity than the other angles. The gain at about 70˚ elevation is about 5 dB higher than that at normal direction. At![]()
, the antenna pattern becomes omni-directional, but the patterns are very directional at all other laminate angles. With![]()
, the substrate becomes less anisotropic (approaching to isotropic substrate), the E-field patterns in Figure 4(b) have less ripples, but the effects of laminate angle on both the antenna resonant frequency and radiation pattern remain. Without accurate modeling, the prediction of antenna performance by assuming substrate of equal permittivity is seriously flawed. Microstrip antenna design on composite substrates with careful selection of substrate laminate angle can achieve better radiation efficiency.
5. Conclusions
1) An electromagnetic model in spectral domain has been applied to investigate the effects of substrate’s laminate angle on antenna performance. The non-diagonal permittivity matrix from different laminate angles comes from the fact that the fiber direction of the laminate layer may not necessarily align with the antenna’s optical axis. Modal analysis shows that the laminate angle has strong influence on antenna design. The resonant frequency of a rectangular microstrip antenna is very much different from that on isotropic or uniaxial substrates. The antenna size deviates lower at all laminate angles, except ![]()
when the substrate is isotropic from mechanics view point.
2) Analyses show that the resonant frequency, and hence the length ratio Liso/ L, varies at different laminate angles, and the variations are more noticeable as thickness increases. The far field patterns show that the maxima will not always be in the normal direction and is dependent on the laminate angle. The performance of a microstrip antenna on composite substrate is very much different from that on isotropic substrate.
Acknowledgements
This work was supported in part by the National Science Council, Taiwan, under NSC100-2221-E006-098-MY3.