Channel Slope Effect on Energy Dissipation of Flow over Broad Crested Weirs ()
1. Introduction
A broad crested weir is usually considered for most hydraulic structures for flow measurement and to control the water surface level in open channels. The water flow type is usually critical conditions. The weirs are of different types such as broad crested, sharp crested and ogee crest weir. The streamline flows over broad crested weir are parallel to the crest, critical depth occur along the crest and the pressure distribution is hydrostatic [1] .
To dissipate energy, step at D/S ends of weirs is constructed or lining by rubbles and riprap is implemented to prevent erosion and scouring in D/S ends [2] .
The flow characteristics over broad crested weirs and single step broad crested weir with rounded upstream (U/S) corner have attracted the attention of several investigators to obtain the flow characteristics and the energy dissipation in numerical and physical methods. [3] studied the characteristics of square and round edge (R) for broad crested weirs under free and submerged flow conditions. Furthermore, they found that the flow separation is essentially eliminated and the coefficient of discharge ( ) has attained the highest value when the ratio of the radius of U/S corner (R) to the height of the weir (P) is (0.25 ≤ R/P ≤ 1). The experimental results of [4] showed that the single step broad crested weir increased the energy dissipation percent up to 46% and was better and gets higher values in comparison with traditional broad crested weirs [5] . Stepped and unstepped weirs were investigated in a laboratory study for steep slope channels in order to find their efficiency for dissipating flow energy. It was found that the maximum energy dissipation ratio in stepped weirs was approximately 10% higher than in unstepped weirs. [6] studied experimentally the effect of channel bed slope on energy dissipation of flow for single step broad crested weir. She found that the maximum energy dissipation ratio was 12.71% for S = 0, P/P1 = 3. The investigation of [7] for single step broad crested weir, showed that the ratio of the length of D/S step to the length of the weir (L2/L1 = 0.5) gives a higher E% in similarity with other weir models.
Several numerical studies were carried out to find the flow characteristics around weirs by Computational fluid dynamics (CFD). The study of [8] simulated a spur dike with three dimensional (3D) and Reynolds averaged Navier Stokes (RANS) equations with the volume of fluid (VOF) and standard k − ε method were used to predict the free surface of flow over weirs. The results of [9] showed that the comparison of the position of the free surface profile over a laboratory rectangular broad crested weir with numerical CFD model. The pressure and velocity measurements were studied numerically on broad crested weir by [10] , where the rapid redistributions of both velocity and pressure fields at the U/S end of the weir crest was predicted. [11] described the validation of CFD for free surface flows over broad crested weir by using a published experimental dataset of [12] and discussed the accuracy of CFD to predict the free surface profile. The [13] studied the free surface profile of water on a broad crested weir by using (VOF). The computational results showed a good agreement with experimental result. [14] employed laboratory study with CFD model that was carried out on broad crested weir located on rectangular channel to predict the Cd value and it gave good agreements between the two values obtained. The relative error of the Cd was 3.043, root mean square errors (RMSE) was 0.123 and mean absolute errors (MAE) was 0.0987. The effect of inclination from 90˚ to 23˚ weir in the U/S face of rectangular broad crested weirs and flow characteristic was studied by [15] using CFD and laboratory model that were applied to improve the performance of broad crested weirs in order to reduce the effect of flow separation. Also, the discharge efficiency was increased 22% higher than the standard weir (90˚) with slope of 23˚.
Iraq has been suffering from severe water shortage problems. One of the main reasons for this shortage is the construction of dams in Turkey and Syria [16] [17] [18] [19] [20] . For this reason, weirs are to be built to regulate the amount of water used and to conserve water in the winter season to be used it in the dry season. If these weirs exist, they can be used to calculate the discharge over their crests, which require the coefficient of discharge (Cd) to be known.
Scaled physical models of weirs have been constructed in hydraulic laboratories to study these behaviors and to calculate the Cd, but they are expensive, time consuming and there are many difficulties associated with scaling effects. Today, with the advance in computer technology, numerical modeling of weirs is becoming increasingly important in the engineering work. For this point, physical modeling can often be replaced by these models.
In this paper, laboratory measurements and 2D numerical modeling were conducted to simulate the flow pattern over a broad crested weir and single step broad crested weir located in a rectangular channel. The results obtained from experimental and numerical work were compared. D/S height of traditional broad crested weir was reduced by a single step; this reduction gave the weir a new performance by making it as an energy dissipater. So, the main objectives of this paper are to study the free surface profile over weir and dissipation energy D/S of the weir for different bed slope of flume ranges (0, 0.002, 0.004) slope channels in laboratory. The experimental result was compared with numerical modeling.
2. Experiments Method
The experimental tests were carried out in the Hydraulic Engineering Laboratory, Collage of Engineering, Al-Mustansiriayah University, Baghdad. The wall and bed of the flume were made of smooth strong glass supported by stainless steel supporting bars at equal distances. The cross section of the flume was 30 cm wide, 30 cm depth and 480 cm long (Figure 1). Three movable point gauges were used to measure water level and traverse apparatus at different static points spaced with 1 mm accuracy were installed at the top of the centerline of flume. Water was supplied through the flume by an electrically pump, which was located in a storage water tank. The flume has a controlling section called scale slope of the flume. The variation slope of channel ranges from S = 0.0, 0.002 and 0.004.
Two weir models were manufactured from steel and well-polished to smooth surfaces and then tested in the laboratory. The first weir was broad crested and the second was single step broad crested weirs which have step at the D/S crest and its height was equal to 7.5 cm. These models can be classified (Figure 2) and in Table 1. In order to
![]() (a)
(a)![]() (b)
(b)
Figure 1.General view of the laboratory flume (a) with broad crested weir (b) with single step broad crested weir.
![]()
Table 1. Details of the tested weir models.
reduce the adverse effects of separations zone, so the two weirs had a radius (R) of rounded corner 2 cm at U/S corner. To ensure the stability and uniformity of water surface levels, models were placed on the bed of the flume at a distance 0.9 m from the flume inlet. In addition, the width of the weirs 30 cm was the same as that of the flume width.
The developments in computer science and numerical techniques have advanced the use of CFD as a controlling tool for analysis of flow over the weirs. In this paper, numerical method was completed by using FLUENT program. FLUENT is one of the great CFD commercial software and it has the capacity to solve 2D and 3D problems of open channel flow, and to predict flow profile over weirs. (VOF) method was used to determine the water surface profile in each cell, which is used in many hydraulic problems because it represent the sharp interface between the air and water phases such as this work [21] .
The governing equations of FLUENT software for unsteady incompressible 2D flows over weirs are continuity. Navier-Stokes equations (Equation (1) and Equation (2)) are based on principles of physics mass conservation and Newton’s Second Law [22] .
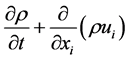 (1)
(1)
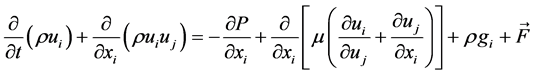 (2)
(2)
where: ρ = fluid density, 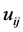 = velocity in X and Y direction, x = space dimensions, t = time, p = the pressure,
= velocity in X and Y direction, x = space dimensions, t = time, p = the pressure, 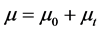 ,
, 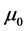 is dynamic viscosity and
is dynamic viscosity and 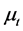 is turbulence viscosity,
is turbulence viscosity, 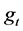 = the body force and = acceleration due to gravity.
= the body force and = acceleration due to gravity.
Turbulent flows are characterized by fluctuating velocity. These fluctuations mix transported quantities such as momentum, energy, kinetic energy and species concentration, and cause the transported quantities to fluctuate as well. Since these fluctuations can be of small scale and high frequency, they are also computationally expensive to simulate directly in practical engineering calculations. Instead, the exact governing equations can be time-averaged, ensemble-averaged, or otherwise manipulated to remove the small scales, resulting in a modified set of equations that are computationally easier to solve and describe [23] .
FLUENT have different turbulent models which includes: k − ε model [standard k − ε model, renormalization group (RNG) k − ε model and realizable k − ε model] and k − ω model [standard k − ω and shear stress transport (sst) k − ω] [24] . However, the numerical models were applied with the k ? ε standard model because its results agreed very well with those obtained from the experiments. In the derivation of the standard (k − ε) model, it was assumed that the flow is fully turbulent, and the effect of molecular viscosity was negligible. The governing equations in this model were turbulent kinetic energy and turbulent energy dissipation rate by using the standard (k − ε) model as follows [25] ;
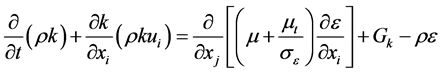 (3)
(3)
where the eddy viscosity μt, is computed by using Equation (5).
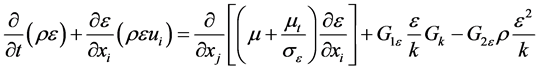 (4)
(4)
where the eddy viscosity μt, is computed by using Equation (5).
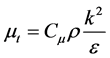 (5)
(5)
where,
Before applying the FLUENT software, the dimensions of weirs must be designed similar to that of the experimental weirs. The first step in numerical method is producing the geometry and creating mesh of the model. For this purpose, GAMBIT software was used. It is noteworthy to mention that GAMBIT can create 2D and 3D meshes. The mesh size of the modeling is an important part of the numerical simulation due to its effect on the accuracy of the result and the simulation time. It was found that the best optimum cell size was 2 mm for the edge and 4.5 mm for the face (Figure 3). This mesh gave the best results in comparison with experimental result.
Boundary conditions in the FLUENT software are one of the most important order of the numerical model of flow and it is should be similar to that of the physical model. In this research, the boundary conditions of the numerical modeling of weirs are shown in Figure 4. Based on Figure 4, the boundary conditions of flow over weirs include the pressure inlet for water and air, pressure outlet, wall and free surface.
3. Results and Discussion
The experimental and numerical results of water surface profiles over broad crested weir and single step broad crested weir along the centerline of the flume with different
![]() (a) (b)
(a) (b)
Figure 3. Zoomed grid near the (a) broad crested weir and (b) single step broad crested weir.
![]()
Figure 4. Boundary condition by using gambit model.
discharge and various sloping of flume were plotted. The water level increased by increased discharge and this lead to the increase of the U/S and D/S water levels. Also, it can be seen from Figures 5-10, the numerical result had a great agreement with experimental results. Where, Y is the water level of flow and X is the horizontal distance of the flume.
![]()
Figure 5. Comparison between exp. and num. method of water surface profile over broad crested weir for different discharge for S = 0.0.
![]()
Figure 6. Comparison between exp. and num. method of water surface profile over broad crested weir for different discharge for S = 0.002
![]()
Figure 7. Comparison between exp. and num. method of water surface profile over broad crested weir for different discharge for S = 0.004.
![]()
Figure 8. Comparison between exp. and num. method of water surface profile over single step broad crested weir for different discharge for S = 0.0.
![]()
Figure 9. Comparison between exp. and num. method of water surface profile over single step broad crested weir for different discharge for S = 0.002.
![]()
Figure 10. Comparison between exp. and num. method of water surface profile over single step broad crested weir for different discharge for S = 0.004.
3.1. Water Surface Profiles
Figure 5 of broad crested weir with S = 0 shown the water surface level is virtually stationary at 0.7 m from the entry of the flume and the flow decreases at the entrance of the weir and cautious with decrease from the U/S edge to the D/S edge of the weir. Also, the flow varied from subcritical flow at U/S edge to critical flow at weir crest. Water surface was parallel to the crest in all runs and the specific energy was minimum, and then passed to supercritical flow at D/S edge. The effect of bed slope on the water level is shown in Figure 6 for S = 0.002 and Figure 7 for S = 0.004. The results showed that the water level had smooth trend and it had a decreasing value along the weir.
Water surface profile of single step broad crested weir with (P/P1 =2) are shown in Figure 8 for S = 0, Figure 9 for S = 0.002 and Figure 10 for S = 0.004. The three figures showed that the water level was stable before reaching the U/S weir edge and passed through the critical depth in the weir crest region where the flow was parallel to this crest then the flow tends to decrease gradually when the flow leaves the weir crest and drop into the crest step. Here the flow changed from gradually varied flow to rapidly varied flow with highly steep decreasing of the flow profile. This clearly reflects the effect of D/S steps on the water surface profiles at this region. Moreover, the water surface profiles from the 2D FLUENT simulated for broad crested weir are shown in Figures 11(a)-(c) and Figures 12(a)-(c) for single step broad crested weir.
3.2. Energy Dissipation (E%)
By applying the energy equations in point (1) and in point (2) in Figure 2, we get the specific energy for two points as:
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
The experimental and numerical models can classified into two weirs based on (P/P1) as broad crested and single step weir, these weirs can be classified into three groups based on the variation of channel slope S = 0.0, 0.002 and 0.004. Each group include twelve running (six for experimental results and six for numerical results) based on the variation of the U/S water head (h).
Figure 13 represented the relation between (h/P) and (E%) of broad crested weir for different slopes in experimental and numerical methods. when S = 0.0 there was a little effect of (h/P) on (E%) because the variation of head in U/S and D/S edge of the weir was very small. The effect of (h/P) on (E%) started to appear at S = 0.002 and became more obvious at the S = 0.004 due to the effect of increasing in the slope. Figure 14 represents the relationship between (h/P) with (E%) of single step broad crested weir
![]() (a)
(a)![]() (b)
(b)![]() (c)
(c)
Figure 11. (a) Numerical water surface profile over a broad crested weir for s = 0.0; (b) numerical water surface profile over a broad crested weir for S = 0.002; (c) numerical water surface profile over a broad crested weir for S = 0.004.
![]() (a)
(a)![]() (b)
(b)![]() (c)
(c)
Figure 12. (a) Numerical water surface profile over a single step broad crested weir for S = 0.0; (b) Numerical water surface profile over a single step broad crested weir for S = 0.002; (c) Numerical water surface profile over a single step broad crested weir for S = 0.004.
![]()
Figure 13. Variation of E% with h/P for broad crested weir of (P/P1 = 1).
![]()
Figure 14. Variation of E% with h/P for single step broad crested weir of (P/P1 = 2).
(P/P1 = 2) for different slopes in experimental and numerical methods. The effect of (P/P1) began to appear with little effect at (S = 0.0), while in the case of S = 0.002 and S = 0.004 the effect obviously appeared on (E%) by increasing it because the effect of single step which decreased the D/S head.
Figure 15 described the variation of the D/S Froude number ![]() with the energy dissipation (E%) of broad crested weir for different slopes in experimental and numerical methods. It can be seen that (E%) increased slightly as (Fr2) increased when S = 0.0. But, in S = 0.002 and S = 0.004 the increase of (E%) was more relative to the former slope. This could be attributed to the reason that as the water level above D/S crest
with the energy dissipation (E%) of broad crested weir for different slopes in experimental and numerical methods. It can be seen that (E%) increased slightly as (Fr2) increased when S = 0.0. But, in S = 0.002 and S = 0.004 the increase of (E%) was more relative to the former slope. This could be attributed to the reason that as the water level above D/S crest ![]() decreases with slope and this lead to increase of the velocity. Therefore; Froude number was increased which is directly proportional to the velocity
decreases with slope and this lead to increase of the velocity. Therefore; Froude number was increased which is directly proportional to the velocity ![]() and inversely with the height
and inversely with the height![]() .
.
The variation of the ![]() with the (E%) of single step broad crested weir (P/P1 = 2) for different slopes in experimental and numerical methods are shown in Figure 16.
with the (E%) of single step broad crested weir (P/P1 = 2) for different slopes in experimental and numerical methods are shown in Figure 16.
It can be noticed that the increase of (E%) was accompanied with the increase of ( ) in all slopes (S = 0.0, 0.002 and 0.004) because the same reason above and the effect of single step which decreased the D/S head respectively. The maximum value of (E%) was 26.9 experimentally and 27.35 in numerically model.
All running details are shown in Table 2. This table also contains the range of Froude number and rang of energy dissipation for experimental and numerical models
![]()
Table 2. Details of the results for experimental and numerical weir models.
![]()
Figure 15. Variation of E% with Fr2 for broad crested weir of (P/P1 = 1).
![]()
Figure 16. Variation of E% with Fr2 for single step broad crested weir of (P/P1 = 2).
and the range of relative error for energy dissipation between experimental and numerical models for each group.
4. Conclusions
In this research, the energy dissipation (E%) and the flow over broad crested and single step broad crested weirs were studied experimentally and simulated by using 2D code (FLUENT software). From this research the following main conclusions were achieved:
1. The VOF method which was used in FLUENT to predict the water surface profile and the result has high agreement with experimental method in all runs.
2. The results showed that the water level along the flow direction was gradually decreasing until it reaches stability condition in D/S side of the flume and the increase in the bed slope made water level smoother and it was reduced in D/S side of the flume.
3. For the two models of weirs (broad crested and single step broad crested weirs), the (E%) value decreased with increased the (h/p) and slop value, the (E%) value increased with increasing the value and with increasing the slope.
4. This research proved the effectiveness of the second model of weir in energy dissipation. While, the maximum value of (E%) in first model was 4.1 in the experimental method and 4.41 in the numerical method at (S = 0.004). Also, the maximum value of (E%) in second model was 26.9 in the experimental method and 27.35 in the numerical method because of the influence of both single step and slope at (S = 0.004) on (E%).
5. Moreover, the ranges of the relative error for first model (P/P1 = 1) in cases S = 0.0, S = 0.002 and S = 0.004 were (1.94 to 6.76), (2.1 to 6.2) and (2.14 to 5.6) respectively. The ranges of the relative error of second model (P/P1 = 2) in cases where S = 0.0, S = 0.002 and S = 0.004 were (1.8 to 5.4), (2.3 to 5.6) and (1.76 to 5.1) respectively.