1. Introduction
Mathematical models described by ordinary differential equations are considered. The equations are linear with respect to unknown constant parameters. Inaccurate measurements of the basic trajectory of the model are given with known restrictions on admissible small errors.
The history of study of identification problems is rich and wide. See, for example, [1] [2]. Nevertheless, the problems stay to be actual.
In the paper a new approach is suggested to solve them. The identification problems are reduced to auxiliary optimal control problems where unknown parameters take the place of controls. The integral discrepancy cost functionals with a small regularization parameter are implemented. It is obtained that applications of dynamic programming to the optimal control problems provide approximations of the solution of the identification problem.
See [3] [4] to compare different close approaches to the considered problems.
2. Statement
We consider a mathematical model of the form
 (1)
(1)
where 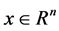 is the state vector,
is the state vector,  ,
, 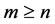 is the vector of unknown para- meters satisfying the restrictions
is the vector of unknown para- meters satisfying the restrictions
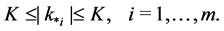 (2)
(2)
Let the symbol 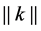 denote the Euclidean norm of the vector
denote the Euclidean norm of the vector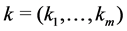 .
.
It is assumed that a measurement  of a realized (basic) solution
of a realized (basic) solution  of Equation (1) is known, and
of Equation (1) is known, and
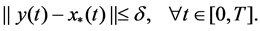 (3)
(3)
We consider the problem assuming that the elements 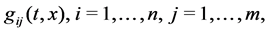 of the
of the  matrix
matrix 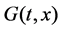 are twice continuously differentiable functions in
are twice continuously differentiable functions in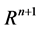 . The coordinates
. The coordinates 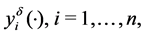 of the measurement
of the measurement 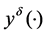 are twice continuously differentiable functions in
are twice continuously differentiable functions in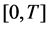 , too. The coordinates
, too. The coordinates  of the vector- function
of the vector- function ![]() are continuous functions on the interval
are continuous functions on the interval![]() .
.
We assume also that the following conditions are satisfied
![]() There exists such constants
There exists such constants ![]() and
and ![]() that for all
that for all ![]() the inequalities
the inequalities
![]() (4)
(4)
are true.
![]() There exist such constant
There exist such constant ![]() (
(![]() from
from![]() ) and such compact set
) and such compact set ![]() that for any
that for any ![]() the following conditions are held
the following conditions are held
![]() ;
;
![]() .
.
Here![]() .
.
The identification problem is to create parameters ![]() such, that
such, that
![]() (5)
(5)
where ![]() is the solution of Equation (1), as
is the solution of Equation (1), as ![]()
3. Solution
3.1. An Auxiliary Optimal Control Problem
Let us introduce the following auxiliarly optimal control problem for the system
![]() (6)
(6)
where ![]() is a control papameter satisfying the restrictions
is a control papameter satisfying the restrictions
![]() (7)
(7)
for a large constant![]() .
.
Admissible controls are all measurable functions![]() . For any initial state
. For any initial state![]() , the goal of the optimal control problem is to reach the state
, the goal of the optimal control problem is to reach the state ![]() and minimize the integtal discrepancy cost functional
and minimize the integtal discrepancy cost functional
![]() (8)
(8)
Here ![]() is the given measurment;
is the given measurment; ![]() is a small regularization parameter,
is a small regularization parameter, ![]() is the trajectoty of the system (6), (7) generated under an admissible control
is the trajectoty of the system (6), (7) generated under an admissible control ![]() out the initial point
out the initial point![]() . The sign minus in the integrand allows to get solutions which are stable to perturbations of the input data.
. The sign minus in the integrand allows to get solutions which are stable to perturbations of the input data.
N o t e 1. A solution ![]() of the optimal control problem (6), (7), (8) allows us to construct the averaging value
of the optimal control problem (6), (7), (8) allows us to construct the averaging value ![]()
![]() (9)
(9)
which can be considered as an approximstion of the solution of the identification problem (1), (2).
3.2. Necessary Optimality Conditions: The Hamiltonian
Recall necessary optimality conditions to problem (6), (7), (8) in terms of the hami- ltonian system [5] [6].
It is known that the Hamiltonian ![]() to problem (6), (7), (8) has the form
to problem (6), (7), (8) has the form
![]()
where ![]() is an ajoint variable, the symbol
is an ajoint variable, the symbol ![]() denotes the transpose operation.
denotes the transpose operation.
It is not difficult to get
![]()
where ![]()
![]()
Here the vector-column ![]() has the form
has the form
![]() (10)
(10)
3.3. The Hamiltonian System
Necessary optimality conditions can be expressed in the hamiltonian form. An optimal trajectory ![]() generating by an optimal admissible control
generating by an optimal admissible control ![]() in problem (6), (7), (8) have to satisfy the hamiltonian system of differential inclusions
in problem (6), (7), (8) have to satisfy the hamiltonian system of differential inclusions
![]() (11)
(11)
and the boundary conditions
![]() (12)
(12)
where symbols ![]() denote Clarke’s subdifferentials [7] and
denote Clarke’s subdifferentials [7] and![]() ,
,![]() .
.
Parameters ![]() belong to the intervals
belong to the intervals ![]() where values
where values ![]() and
and ![]() are choosen from the conditions
are choosen from the conditions
![]() (13)
(13)
We introduce the last important assumption.
![]() There exists a constant
There exists a constant ![]() such that restrictions on controls in problem (6), (7), (8) satisfy the relations
such that restrictions on controls in problem (6), (7), (8) satisfy the relations
![]() (14)
(14)
![]()
where ![]() are from (10).
are from (10).
N o t e 2. Using definition (10) one can check that constant K, satisfying assumtion![]() ,
, ![]() can be taken as
can be taken as
![]() ,
,
where
![]()
Here![]() are components of matrix
are components of matrix ![]() and
and ![]() are components of matrix
are components of matrix![]() .
.
If ![]() and
and ![]() the Hamiltonian has the simple form
the Hamiltonian has the simple form
![]()
and the differential inclusions (11) transform into the ODEs.
![]() (15)
(15)
Let us introduce the discrepancies![]() , and obtain from (15) the following equations
, and obtain from (15) the following equations
![]() (16)
(16)
and the boundary conditions
![]() (17)
(17)
where ![]() saisfy (13).
saisfy (13).
3.4. Main Result: Dynamic Programming
Using skims of proof for similar results in papers [8] [9] [10] we have provided the following assertion.
Theorem 1 Let assumptions ![]() be satisfied and the concordance of para- meters
be satisfied and the concordance of para- meters![]() :
: ![]() takes place, then solutions of problem (11), (12), (13)
takes place, then solutions of problem (11), (12), (13) ![]() are extendable and unique on
are extendable and unique on ![]() for any
for any ![]() saisfying (13) and
saisfying (13) and
![]() (18)
(18)
It follows from theorem 1, that the average values ![]() (9) obtained with the help of dynamic programmig satisfy the desired relation
(9) obtained with the help of dynamic programmig satisfy the desired relation
![]() (19)
(19)
4. Numerical Example
A series of numerical experiments, realizing suggested method, has been carried out. As an example a simple mechanical model has been taken into consideration.
This simplified model describes a vertical rocket launch after engines depletion. The dynamics are described as
![]() (20)
(20)
where ![]() is a vertical coordinate of the rocket,
is a vertical coordinate of the rocket, ![]() is an unknown windage coefficient and
is an unknown windage coefficient and ![]() =9.8 is a free fall acceleration.
=9.8 is a free fall acceleration.
A function ![]() is known and satisfies assumption
is known and satisfies assumption![]() . This function was obtained by random perturbing of the basic solution
. This function was obtained by random perturbing of the basic solution ![]() for
for ![]() =0.3.
=0.3.
The suggested method is applied to solve the identification problem for ![]() = 0.3.
= 0.3.
We introduce new variables ![]() and transform Equation (20) into
and transform Equation (20) into
![]() (21)
(21)
where ![]() and
and ![]() is a fictitious control, which was introduced in order to get
is a fictitious control, which was introduced in order to get ![]() matrix
matrix ![]() in (1) satisfying dimentions restriction
in (1) satisfying dimentions restriction![]() .
.
We put![]() .
.
The corresponding hamiltonian system (16) for problem (21),(8) has the form
![]() (22)
(22)
with initial conditions
![]() (23)
(23)
The solutions were obtained numerically. On the Figure 1 and Figure 2 the graphs
![]()
Figure 1. k(t) graph for δ = 5; k(α, δ) = 0.375.
![]()
Figure 2. k(t) graph for δ = 2; k(α, δ) = 0.325.
of functions ![]() are exposed. The graphs illustrate convergence of the suggested method. The calculated corresponding average values (9) are exposed as well.
are exposed. The graphs illustrate convergence of the suggested method. The calculated corresponding average values (9) are exposed as well.
Acknowledgements
This work was supported by the Russian Foundation for Basic Research (projects no. 14-01-00168 and 14-01-00486) and by the Ural Branch of the Russian Academy of Sciences (project No. 15-16-1-11).