Perturbation-Iteration Method for Solving Mathematical Model of Glucose and Insulin in Diabetic Human during Physical Activity ()
1. Introduction
The most important mechanisms leading to following chronic diseases among them there are non-communicable diseases. The development of cardiovascular and metabolic disorders depends on the complex interplay of multiple anatomic and physiologic factors but the mechanism behind these factors and their impacts on the type or degree of the disorder, experimental observations or on the treatment responses remain poorly understood. Therefore, most patients today are being treated with general therapies regardless of the cause of dysfunction. We believe that combining experimental measurements with mathematical modeling will provide important information on the individual key dysfunction, making it possible to start developing personalized therapies. Similarly as observations from data can inspire new theoretical models, the models can translate the measurements first into new ideas, then into testable hypotheses and finally into medical knowledge. Such model-based investigations can therefore provide systematic strategies toward better understanding, predicting or even preventing the disorders.
Naturally human bodies are made in such way that the level of glucose concentration must be maintained in the range of 70 - 120 mg/dl or 3.9 - 6.7 mmol/l. This means that when an individual’s glucose concentration level is found out of that normal range, the said person is judged to have the plasma glucose problems which should be classified in two categories: 1) it can happen Hyperglycemia, this is when the level is greater than 140 mg/dl or 7.8 mmol/l after an Oral Glucose Tolerance Test, or greater than 100 mg/dl or 5.5 mmol/l after a Fasting Glucose Tolerance Test. 2) Alternatively it can happen Hypoglycemia, that is when the level is less than 40 mg/dl or 2.2 mmol/l. On one hand, a prolonged hyperglycemia that is seen to be the major long-term effect of diabetes can cause complications, which may lead to kidney disease, blindness, loss of limbs, and so on. On the other hand, the hypoglycemia can lead to dizziness, coma, or even death. Human body has two main organs that play an important role in regulating blood glycose measurements; those organs are pancreas and liver. During the process of controlling blood glycose, insulin and glucagon are hormones that are mainly involved in that process of controlling glucose. In the pancreas, there are clusters of endocrine cells glucose and insulin. These are the α-cells and the β-cells. The α-cells produce glucagon and the β-cells produce insulin. The pancreas secretes these antagonistic hormones into the extracellular fluid, which then enters the circulatory system and regulates the concentration of glucose in the blood. For biologists, this is known as a simple endocrine pathway. Diabetes Mellitus is an endocrine disorder caused by a deficiency of insulin (Type I Diabetes) or a decreased response to insulin in target tissues (Type II Diabetes) [1] . Type I Diabetes was previously called insulin-dependent diabetes mellitus (IDDM) or juvenile-onset diabetes. It is an autoimmune disorder in which the immune system destroys the β-cells of the pancreas. As a result, the person’s ability to produce insulin is greatly inhibited. About 90% to 95% of people with diabetes have type II and many can manage their blood glucose level with regular exercise and a healthy diet; however, some require drug therapy.
Worldwide diabetes disease and human glucose-insulin balance motivated researchers in various directions such as studies on 1) glucose-insulin endocrine metabolic regulatory system [2] [3] [4] [5] [6] , 2) what cause the dysfunctions of the system [1] , 3) how to detect the onset of the either type of diabetes including the so called pre-diabetes [7] [8] [9] [10] , and 4) methods for solving mathematical models of glucose and insulin in human body during physical activity [11] [12] . In the findings of those studies, reasonable, effective, efficient and economic treatments to diabetics are suggested. Since the 1960s, researches in the direction of solving mathematical models have been developed to describe glucose-insulin dynamic systems [1] [13] . On one hand, some of those models are oriented towards analysis of the glucose disappearance and insulin sensitivity during an intravenous glucose tolerance test [14] and capture of plasma glucose and insulin dynamics during, as well as after, periods of mild-to-moderate exercise [15] . On the other hand, others focus on overestimation of glucose effectiveness and the under- estimation of insulin sensitivity [16] , capture absorption, distribution and disposal dynamics [17] . Recently, a mathematical model has been developed to capture the integral impact of physical activity to dynamic systems [11] . As glucose and insulin are found in blood and must circulate in all parts of the human body, this fact allows to include these mathematical models in the field of dynamic systems which are governed by ordinary differential equations. The mathematics properties of the dynamic systems of glucose and insulin have been done by some researchers [2] [9] and [18] . The numerical resolution of mathematical models that are based on ordinary differential equations can be done using different numerical methods. The recent method that can be used has been derived in [19] : Perturbation-iteration method. This paper focuses on this new important method.
The current study is framed in six sections. Section one introduces to the audience the motivation of model-based investigation, background on previous research in the domain of dynamical systems related to glucose and insulin and the structure of the paper. In section two, we present the mathematical model of ordinary differential equations. The section three deals with the basic idea of the perturbation-iteration method. The numerical simulation is presented in section four where the comparison is done using Euler method and Runge Kutta methods to test efficiency of perturbation-iteration method. The section five focuses on discussion while section six rounds up and deals with the concluding remarks.
2. The Mathematical Model Equations
In the work [12] when dealing with the setting of mathematical model equations, the author highlights on the description of a compartmental two delay mathematical model of glucose and insulin during physical activity. In the description, it is noted that although the plasma glucose is disturbed from its equilibrium, but human body uses to provide other metabolic variables to maintain equilibrium. This metabolic process is referred to glucose effectiveness where to return on the equilibrium state, the delays affect significantly the process. In this context Hovolka and Cordingley [17] confirm that the simplification of glucose by parental glucose infusion can be done in three modes: 1) reducing the delays associated with glucose kinetics, 2) decreasing the proportion of insulin appearance as a consequence of endogenous component and 3) reducing the proportion of glucose fluxes due to endogenous origin. Moreover, the description underlines that long time delays is a barrier to determine the insulin dose needed to achieve and maintain tight glucose control. Thus changes in plasma glucose concentrations that may result in serious and dangerous consequences are enhanced by hyperglycemia [20] which may finally lead to cardiovascular disease in diabetic patients [21] . Fortunately, these days insulin plays an important role in treating diabetes. It is usually delivered subcutaneously, which delays the effect of the insulin in the blood as compared with to natural insulin in healthy persons that is secreted directly into the circulatory system. Human insulin is found in what is called hexamer form and the subcutaneous absorption of insulin in the hexamer form is really slow. This was experimented for the first time by Kadish in 1964 [22] closing the control loop in a patient with diabetes, it has been shown that the control action (insulin) that is delivered throughout intravenous mode minimizes the insulin transport delays in tissues.
To clarify the mathematical model of our study, reference is made to [11] where human physical activity is called upon purposing to regulate the plasma glucose level and in improve insulin sensitivity. On one hand, human physical activity leads to the variation physiological parameters that are function of heart rate and alveolar ventilation. On the other hand, human cardiovascular respiratory system cannot work properly without the inclusion of the flow of plasma glucose and insulin in liver (LC) and pancreas (PC) compartments. Due the fact that cardiovascular respiratory system is regulated by heart rate H and alveolar ventilation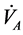 
via arterial pressure (PA) and venous pressure (PV), our mathematical model is made up in such way that they are take into account. In addition blood flows between lungs and heart due to left (Ql) and right (Qr) cardiac output. Consequently, arterial pressure leads the tissues to receive the blood from cardiovascular respiratory system whereas the blood comes to cardiovascular respiratory system from tissues due to the arterial pressure. However, the respiratory control system varies the ventilation rate in response to the levels of dioxide CO2 and oxygen O2 gases. Consequently, ventilation rate and cardiac output influence each other mutually. Therefore exchanges between LC and PC are controlled by heart rate and alveolar ventilation functions. This mechanism of controlling is not straightforward rather it is represented by outflow functions between systemic arterial and venous compartments that depend on heart rate and alveolar ventilation (Figure 1).
Therefore a nonlinear compartment analysis leads on the following new global model
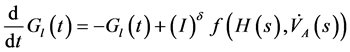(1)
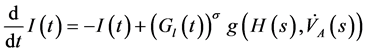(2)
where the functions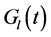 
and 
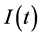denote respectively glucose and insulin at time t, δ and σ are model constants and f, g model functions to be identified. System of nonlinear ordinary differential Equations (1) and (2) came from straightforward development of mass balance between glucose and insulin compartments.
Here physical activity comes in to play the role of maintaining glucose concentration level in a narrow range and to improve insulin sensitivity for the case of Type II diabetes. The numerical simulation is carried on three types of regular physical activity (physical exercise of 30 minutes per day) for a 30 years old woman: Walking, Jogging and Running Fast. We consider the following identified functions f and g as presented in [11] .
![]()
Figure 1. A schematic diagram of two compartments for modeling human glucose-insulin. Ql and Qr are left and right cardiac flow respectively. H is heart rate and 
denotes alveolar ventilation. PA and PV represent arterial and venous pressure respectively
Constants δ and σ are set as in [11] that is
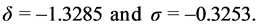
3. Perturbation-Iteration Algorithm (PIA)
Perturbation-iteration method has been developed recently by Aksoy and Pakdemirli [19] . This new method of solving a system of first order of nonlinear ordinary differential equations uses a combination of perturbation expansions and Taylor series expansions to give rise to an iteration scheme where Aksoy and Pakdemirli [19] and Pakdemirli et al. [23] introduced expansion and correction terms of only first derivatives in the Taylor series expansion and one correction term in the perturbation. Therefore, the perturbation-iteration algorithm is named by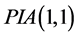
. Let us be interested in the description of
.
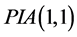First of all, we discuss the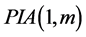 
which is constructed by taking one correction term in the perturbation expansion and correction terms of m’th order derivatives in the Taylor Series expansion. We consider a system of first order of K nonlinear ordinary differential equations. We note
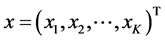
a vector state. The system first order of K nonlinear ordinary differential equations can be written as follows
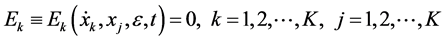
where ε is the perturbation parameter and t denotes the independent variable. That is the system
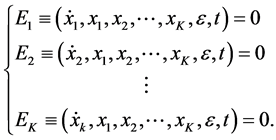(3)
Taking an approximate solution of the system (3) as
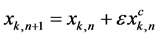(4)
where subscript n represents the n’th iteration over this approximate solution, we have a solution with one correction term in the perturbation expansion. The system can be approximated with a Taylor series expansion in the neighborhood of ε = 0
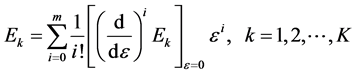(5)
where
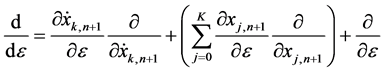(6)
is defined for the (n + 1)’th iterative equation
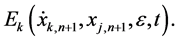
Substituting (6) into (5), we obtain an iteration equation
![]()
(7)
which is a first order differential equation and can be solved for the correction terms![]()
. Then using (4), the (n + 1)’th iteration solution can be found. Iterations are terminated after a successful approximation is obtained.
Note that for a more general algorithm, n correction terms instead of one can be taken in expansion (4) which would then be a ![]()
algorithm. The algorithm can also be generalized to a differential equation system having arbitrary order of derivatives (see [24] for more details).
After the discussion of![]()
, now we focus on ![]()
which is its simple case of perturbation-iteration method![]()
.
We consider the general cause of first order of differential equation as
![]()
(8)
where![]()
. Taking one correction term in perturbation expansion, we have
![]()
(9)
where n denotes the n’th iteration over this approximate solution such that for the perturbation parameter ε the expression ![]()
represents the correction term. Substitution of (9) into (8) we obtain
![]()
(10)
Reorganizing Equation (10), we have
![]()
(11)
where ![]()
and all derivatives are evaluated at ε = 0. Setting
![]()
as integrating factor, our equation is now transformed into the form
![]()
so that
![]()
that is
![]()
(12)
Substitution of (12) into (9) and constructing the iteration scheme yields
![]()
4. Numerical Simulation
We consider the rest values of unhealthy woman. Therefore we take 180 mg/dl and 2.1 μU/dl for plasma glucose and insulin respectively. The equilibrium values (values for healthy person) of plasma glucose and insulin are taken as 100 mg/dl and 3.5 μU/dl respectively.
To show the effectiveness of![]()
, we focus on the numerical simulation of the system (1)-(2) by taking the observed values presented in Table 1 [11] for three case of physical activities that is walking, jogging, running fast.
Taking ![]()
and ![]()
hear rate and alveolar ventilation at the equilibrium states, the system (1)-(2) is written as
![]()
(13)
![]()
(14)
where
![]()
The system (1)-(2) is solved by using![]()
. The perturbation parameter ε is artificially introduced as
![]()
(15)
Setting![]()
, we want an approximate solution of the system of the form
![]()
(16)
with one correction term in the perturbation expansion such that the relation (7) is satisfied for
![]()
![]()
Table 1. The mean value of the heart rate, the alveolar ventilation, venous and arterial systemic pressure for the rest and three cases of physical activities. Apart the rest, other numbers represent equilibrium values related to 30 years old woman’s three physical activities.
For (15), Equation (7) reduces to
![]()
(17)
with the solution
![]()
(18)
and
![]()
, (19)
where ![]()
and ![]()
are constants of integration that have to be determined at each iteration from initial guess satisfying the initial condition if (16) is applied.
Using the values from Table 1, we obtain the values of ![]()
and ![]()
as shown in Table 2 for three cases of physical activity.
After substituting initial guess in (17) and with the help of Equation (16), the first following approximation has been obtained in applying the iteration formula (18) and (19).
・ Walking case:
![]()
・ Jogging case:
![]()
・ Running fast case:
![]()
To test the efficiency of perturbation iteration algorithm ![]()
we compare the results with two others obtained using two different methods which are Euler method and Matlab approach for solving system of ordinary differential equations (ODEs). The Matlab approach has been implemented using its ODEs solver from Runge-Kutta of order 4 and 5, this is ode45. The numerical results are illustrated in Figure 2, Figure 3 and Figure 4.
![]()
Table 2. The values fe and ge for three cases of physical activity.
![]()
Figure 2. Variation trajectory of plasma glucose Gl (a) and insulin I (b) for a 30 years old woman during walking physical activity. Three curves are compared using three different methods: Perturbation-iteration algorithm (Solid line), Euler method (dashed line) and Matlab approach (Dot line).
![]()
Figure 3. Variation trajectory of plasma glucose Gl (a) and insulin I (b) for a 30 years old woman during jogging physical activity. Three curves are compared using three different methods: Perturbation-iteration algorithm (Solid line), Euler method (dashed line) and Matlab approach (Dot line).
![]()
Figure 4. Variation trajectory of plasma glucose Gl (a) and insulin I (b) for a 30 years old woman during running fast physical activity. Three curves are compared using three different methods: Perturbation-iteration algorithm (Solid line), Euler method (dashed line) and Matlab approach (Dot line).
5. Discussion
The heart rate and the alveolar ventilation are two controls of the cardiovascular-respi- ratory system. Consequently they have a great influence in controlling other parameters that flow through this system such as plasma glucose and insulin. Furthermore, the stability of each of those controls at the equilibrium value allows plasma glucose to reach a stabilized state and insulin to be around its sensitivity value. The response of these controls to the plasma glucose and insulin are represented in Figure 2, Figure 3 and Figure 4 where all methods used show that plasma glucose decreases at the beginning of physical activity and it is stabilized when it reaches the corresponding equilibrium value (see Figure 2(a), Figure 3(a) and Figure 4(a)). This shows a perfect representation of the importance of physical activity in the regulation of parameters related to diabetes, particularly the stability of plasma glucose during exercise. Figure 2(b), Figure 3(b) and Figure 4(b) show the behavior of insulin sensitivity which increases from the beginning of physical activity in order to be around its sensitivity value. The results obtained in this work are rather satisfactory. In particular, the response of controls of cardiovascular-respiratory system to plasma glucose and insulin has an influence in regulation of those parameters. The feedback can be proved using numerical simulation of mathematical model governed by ordinary differential system. Physical activity reduces any chronic disease and it induces important changes in the stabilization of cardiac, vascular and blood tissue.
6. Concluding Remarks
We have investigated in this work a new numerical method for solving a system of ordinary differential equations: Perturbation Iteration method. The efficiency of this method is tested using two other convergent methods that are Euler method and Runge- Kutta method. Those all methods are implemented using Matlab packages. The numerical simulations illustrate the responses of plasma glucose and insulin due to the control of heart rate and alveolar ventilation of cardiovascular-respiratory system. The numeri- cal results confirmed the analytical analysis for a 30 years old woman during three different physical activities: Walking, Jogging and Running fast.