1. Introduction
Digital Phase Locked Loop (PLL) has been widely used and for many years in wireless and wired communications subsystems. It is an essential component in clock and carrier recovery, and frequency synthesizer. Digital Phase locked Loops (DPLLs) have better reliability and higher stability compared to analogue counterpart at lower cost and can easily be part of a digital processing equipment [1] . The researchers show strong interest in the design of digital PLLs (DPLLs) to solve problems associated with analog DPLLS, such as, sensitivity to DC drift and component inaccuracies and saturation, and their need for initial calibration [1] [2] . The sampler type classifies DPLL into two major categories: uniform sampling DPLLs (US-DPLLs) and non-uniform sampling DPLLs (NUS-DPLLs). Different types of NUS-DPLLs have been introduced according to the way to detect the phase difference between locally generated carrier and the input signal to the loop from the sampled signal such as zero crossing DPLL (ZCDPLL) [3] [4] and digital tan-lock loop (DTLL) [5] [6] [7] . ZCDPLL is a closed loop system used to follow the zero crossing of the input carrier signal. It consists of a sampler (acting as a phase detector), a digital loop filter and a digital controlled oscillator [8] [9] [10] [11] . The most commonly used DPLL is the Zero Crossing Digital Phase Locked Loop (ZCDPLL). The operation is based on tracking the signal input phase by using non uniform sampling techniques. The sample value is a function of the signal input phase. These values are filtered before they are used back to control the next sampling time by the help of Digital Controlled Oscillator (DCO). The non-linear behaviour of ZCDPLL leads bifurcation instabilities to its path to chaos [12] .
A number of methods were proposed for chaos control [13] such as using Pyragas method to broaden the tracking range by extending the stable operation behaviour of ZCDPLL to a larger digital filter gain, which leads to larger input frequency [11] . Fixed Point Iteration (FPI) with relaxation will be presented to extend the stable operation range of both first and second order ZCDPLL. The stabilized loops are analyzed and the results are verified using bifurcation theory and a numerical simulation. It is the first time that FPI used to stabilize the chaotic operation of the DPLL.
In Section 2, the conventional first order ZCDPLL operation is described. Section 3 discusses the Fixed Point stabilization algorithm, and in section 4 the second order ZCDPLL is presented, while Section 5 details the operation of the second order ZCDPLL when FPI chaos control is included in the loop. Simulation results are presented in Section 6 and finally conclusions are given in Section 7.
2. First Order ZCDPLL
Conventional first order ZCDPLL is shown in Figure 1. Let us assume that the input signal 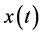 is defined as
is defined as

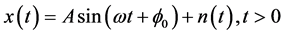 (1)
(1)
where  is Additive White Gaussian Noise (AWGN),
is Additive White Gaussian Noise (AWGN),  is initial phase (can be assume zero without loosing generality),
is initial phase (can be assume zero without loosing generality),  is the input signal frequency, and
is the input signal frequency, and 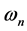 is the nominal frequency or DCO free running frequency when no input signal is applied. The input signal is assumed to be noise free [
is the nominal frequency or DCO free running frequency when no input signal is applied. The input signal is assumed to be noise free [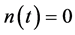 ]. This input signal
]. This input signal  is sampled at
is sampled at 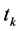 instants determined by DCO.
instants determined by DCO.
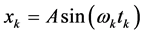 (2)
(2)
the sampling instants 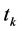 can be represented by
can be represented by
![]()
Figure 1. Block diagram of conventional first ZCDPLL.
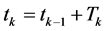 (3)
(3)
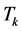 is the Digital Controlled Oscillator (DCO) period, which is given by [15] :
is the Digital Controlled Oscillator (DCO) period, which is given by [15] :
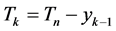 (4)
(4)
where 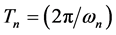 is the nominal period,
is the nominal period, 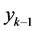 is the output of digital filter. The input signal phase can be represented as
is the output of digital filter. The input signal phase can be represented as![]() . The sampled signal input
. The sampled signal input ![]() will be
will be
![]() . (5)
. (5)
The phase error ![]() is determined by:
is determined by:
![]() . (6)
. (6)
Then
![]() . (7)
. (7)
The sampled values ![]() is passed through a digital filter D(z) to produce the output
is passed through a digital filter D(z) to produce the output![]() . The digital loop filter can be of zero order (just gain block) or first order (gain and summation blocks). The loop filter output
. The digital loop filter can be of zero order (just gain block) or first order (gain and summation blocks). The loop filter output ![]() can be written as:
can be written as:
![]()
where K is the zero order filter gain (First Order ZCDPLL), while for first order filter or second order ZCDPLL, the outputs will be:
![]() (8)
(8)
where ![]() and
and ![]() are the loop filter gains. If a frequency step of a value
are the loop filter gains. If a frequency step of a value ![]() is applied to the ZCDPLL (
is applied to the ZCDPLL (![]() ), then the signal input phase can be expressed as:
), then the signal input phase can be expressed as:
![]()
![]()
![]()
![]()
![]() (9)
(9)
where ![]() is normalized frequency step size. Consequently the phase error can be written as
is normalized frequency step size. Consequently the phase error can be written as
![]()
![]() . (10)
. (10)
Therefore first order ZCDPLL phase error operation function will be:
![]() . (11)
. (11)
The phase error mapping function (![]() ) will be:
) will be:
![]() . (12)
. (12)
3. Extending the Stable Operation of First Order ZCDPLL
Various methods and techniques were used to control the instability of chaotic operation of control loop such as Ott-Grebogi-Yorke (OGY) or Pyragas [14] . In this paper the Fixed Point Iteration (FPI) with relaxation is used to extend the stable operation of the ZCDPLL. FPI was used the first time by Babylonian (2000 B.C) to estimate the square root. The original version was used for finding ![]() as:
as:
![]() . (13)
. (13)
Then Hillam [16] proposed FPI with relaxation for fixed point stability as follow:
![]() (14)
(14)
p is fractional constant which control the amount of feedback. This algorithm can’t be used when ![]() (non-hyperbolic fixed points (8, 9). Let us apply the above FPI with relaxation to stabilize ZCDPLL operation. Then the operation Equation (12) should become as:
(non-hyperbolic fixed points (8, 9). Let us apply the above FPI with relaxation to stabilize ZCDPLL operation. Then the operation Equation (12) should become as:
![]()
![]() . (15)
. (15)
The system will be stable when![]() . This condition of the derivative of Equation (15) will be:
. This condition of the derivative of Equation (15) will be:
![]()
where![]() . The stable operation phase error (
. The stable operation phase error (![]() ) was found to be at
) was found to be at ![]() [15] . The values of the constant (p) which can stabilize ZCDPLL operation is determined from Equation (16). The values are
[15] . The values of the constant (p) which can stabilize ZCDPLL operation is determined from Equation (16). The values are
![]()
The stabilized first order ZCDPLL using FPI with relaxation is shown in Figure 2.
4. Second Order ZCDPLL Operation
The first order filter transfer function ![]() of the second order ZCDPLL can be written as:
of the second order ZCDPLL can be written as:
![]()
![]()
Figure 2. FPI chaos controlled first order ZCDPLL.
Then ![]() is expressed as
is expressed as
![]() (16)
(16)
![]() . (17)
. (17)
To express Equation (16) in time domain:
![]()
Then the operation Equations (10) is given by [17]
![]() (18)
(18)
![]() (19)
(19)
If we assume![]() ,
, ![]() , then the second order ZCDPLL operation equation can be written as
, then the second order ZCDPLL operation equation can be written as
![]() (20)
(20)
To guarantee the stable operation of the loop, then inequality should be satisfied [17]
![]() (21)
(21)
5. Extending the Stable Operation of Second Order ZCDPLL
The proposed FPI with relaxation for fixed point stability is applied for second order as well and the new operation equation can be written as:
![]() (22)
(22)
The system state vector is defined as![]() ,
, ![]() ,
,![]() . Then
. Then
![]() (23)
(23)
around the stable operating point![]() ,
,![]() . The Jacobian
. The Jacobian ![]() is given by
is given by
![]() (24)
(24)
In order to have eigen values of ![]() less than 1, or
less than 1, or![]() , where
, where ![]() satisfies the characteristic equation
satisfies the characteristic equation ![]() in [17]
in [17]
![]() (25)
(25)
Using Jury stability test [18] , the roots of the polynomial ![]() defined in (25) are within a unit circle, or the eigen values are less than 1, if
defined in (25) are within a unit circle, or the eigen values are less than 1, if ![]() greater than 0. Then p should satisfies the following:
greater than 0. Then p should satisfies the following:
![]()
![]()
![]() (26)
(26)
Since ![]() or
or ![]() this leads that
this leads that![]() . Jury stability test ap-
. Jury stability test ap-
plied on ![]() the absolute value of the constant term of the equation should be less than 1. This leads to
the absolute value of the constant term of the equation should be less than 1. This leads to
![]()
![]()
![]() (27)
(27)
6. System Performance
The first and second order conventional and FPI chaos controlled ZCDPLL is simulated by using MATLAB. The input signal is assumed to be ![]() with peak amplitude of 1 volt and angular frequency of
with peak amplitude of 1 volt and angular frequency of![]() . The free running fre-
. The free running fre-
quency of DCO is ![]() or
or![]() . During simulation, the first 100 samples of the DCO period (
. During simulation, the first 100 samples of the DCO period (![]() ) values are discarded to allow the loop to stabilize. The next 100,000 samples are collected and recorded to generate bifurcation plot. The bifurcation plot maps the
) values are discarded to allow the loop to stabilize. The next 100,000 samples are collected and recorded to generate bifurcation plot. The bifurcation plot maps the ![]() values versus the filter gain(s). It will be used to compare the operation ranges of the conventional and FPI chaos controlled ZCDPLL.
values versus the filter gain(s). It will be used to compare the operation ranges of the conventional and FPI chaos controlled ZCDPLL.
First order ZCDPLL is subjected to a frequency step of 1.3 Hz. Then ![]() values are recorded for three cases. The first case shown in Figure 3(a) is for conventional ZCDPLL. The conventional loop bifurcates at
values are recorded for three cases. The first case shown in Figure 3(a) is for conventional ZCDPLL. The conventional loop bifurcates at![]() . DCO period jitter is used to show the amount of deviation of the period compared to the input signal period (jitter
. DCO period jitter is used to show the amount of deviation of the period compared to the input signal period (jitter
=![]() , where T is input signal period). Figure 3(b) shows that FPI chaos
, where T is input signal period). Figure 3(b) shows that FPI chaos
controlled first order ZCDPLL bifurcates![]() , which is higher than for conventional loop (Chaos control constant
, which is higher than for conventional loop (Chaos control constant ![]() was used in this test). This agrees with the theoretical analysis presented earlier. Figure 3(c) shows how adaptive values of the constant (p) (Equation (16)) can be used to continuously stabilize the loop by changing its values according to filter gain (
was used in this test). This agrees with the theoretical analysis presented earlier. Figure 3(c) shows how adaptive values of the constant (p) (Equation (16)) can be used to continuously stabilize the loop by changing its values according to filter gain (![]() ).
).
There are two filter parameters in the second order loop (![]() ). In these simulations we fixed the gains ratio (
). In these simulations we fixed the gains ratio (![]() ) and vary
) and vary ![]() value. Figure 4 shows clearly
value. Figure 4 shows clearly
that the FPI chaos controlled loop has extended stable operation when the filter parameter (![]() ) varied. Gains ratio used here is
) varied. Gains ratio used here is![]() , and the chaos control constant is set to be (
, and the chaos control constant is set to be (![]() ). The conventional ZCDPLL bifurcates at
). The conventional ZCDPLL bifurcates at ![]() while the FPI chaos controlled loop bifurcate after
while the FPI chaos controlled loop bifurcate after![]() . Figure 5 shows that even the filter gains ration (r) is increased to 1.6, that the loop still has extended operation range as well. The conventional loop bifurcates at
. Figure 5 shows that even the filter gains ration (r) is increased to 1.6, that the loop still has extended operation range as well. The conventional loop bifurcates at![]() , while the FPI chaos controlled loop starts to bifurcate at
, while the FPI chaos controlled loop starts to bifurcate at![]() . If the filter gains ratio r is further increased as shown in Figure 6, the FPI chaos controlled will be unstable. This means that the chaos control constant (p) should be carefully chosen according to the inequality that is derived in this paper.
. If the filter gains ratio r is further increased as shown in Figure 6, the FPI chaos controlled will be unstable. This means that the chaos control constant (p) should be carefully chosen according to the inequality that is derived in this paper.
![]()
Figure 3. First order FPI-ZCDPLL performance for different values of p.
![]()
Figure 4. Second order FPI-ZCDPLL performance for different values of p and![]() .
.
![]()
Figure 5. Second order FPI-ZCDPLL performance for different values of p and![]() .
.
![]()
Figure 6. Second order FPI-ZCDPLL performance for different values of p and![]() .
.
7. Conclusion
This paper proposes a Fixed Point Iteration (FPI) with relaxation to control the chaotic operation of the ZCDPLL. The analytic expressions for the stable operation for both conventional and FPI chaos control first and second order ZCPLL are found and confirmed by simulation. It is found that the lock range of the FPI chaos controlled loop is larger than that of the conventional loop for both orders. The validity of the results is conformed through numerical simulations. It is also found that careful selection of chaos control parameters is needed to ensure that the loop is still working in stable operation. This extended operation of the ZCDPLL leads to larger lock range. The larger values of filter gains of FPI chaos controlled will automatically decrease the input signal acquisition time.