Model Based Pressure Control of a Push Belt Continuously Variable Transmission ()
1. Introduction
Mandates to reduce carbon emissions and increase the fuel economy of vehicles have gained prominence in the recent years with the declining fuel resources and increased effects of global warming. Automakers have been trying to achieve the maximum fuel economy possible from their vehicle fleet to achieve the strict Corporate Average Fuel Economy (CAFE) targets. All this has led to a lot of research on vehicle technologies, including hybridization and electrification. In this regard, Continuously Variable Transmission (CVT) holds greater promise to improve the fuel economy of vehicles.
CVTs are available in various forms, including the commonly used push-belt type CVTs, the Toroidal traction drive, the variable diameter elastomer belt, and the variable geometry CVT. Since late 90s, the CVT research has gained prominence, these researches were conducted to understand the mechanics of CVT, the role of friction and the influence of control strategies on the performance and efficiency of the vehicle powertrain, the details of these researches are reviewed by Srivastava and Haque [1] .
A CVT enables to have continuous range of gear ratios between certain limits that help in increasing the overall powertrain efficiency by running the engine at its optimal operating point while providing a smooth speed-torque curve. Therefore, CVT eliminates the shifting jerks in comparison to conventional automatic transmissions, resulting in an improved driver feel. However, the overall CVT efficiency is heavily dependent on the parasitic loads needed to actuate and control the pulleys hydraulically.
Despite the inherent benefits discussed above, CVTs market share showed a large market penetration resistance during 2000s, but after the new CAFE regulations and the advances in CVT controls and designs, National Research Council [2] estimated a 19.3% market share in 2014. Further, the market resistance of CVTs is due to the inherent issue of belt slip, limited torque capacity and cost. The control of CVTs is complicated as they are usually non-linear systems. Thus, CVT control had become a major topic of research and control models are being developed to reduce the complexity associated with CVTs.
This paper addresses CVT control problem using a model-based pressure control strategy to achieve the desired speeds. The paper is divided into the following sections. Section II gives an overview of the working principle of a CVT and the literature. Section III describes different control approaches available today. Section IV describes the model that has been developed to represent a CVT in an actual vehicle. Section V details the control strategy used. Section VI presents the results. Section VII provides the conclusions.
2. Push-Belt CVT―Overview
The push-belt CVT, Figure 1, consists of a metal push-belt that connects the primary (driver) with the secondary (driven) pulley. Each pulley has a fixed sheave and a movable sheave. If the linear displacement of the movable sheaves in both pulleys is restricted, then a constant gear ratio is maintained. However, to change the gear ratio, the movable sheaves have to be displaced equally and oppositely, as shown in Figure 1. The displacement of the movable sheaves is controlled hydraulically, and accordingly the hydraulic pressure develops a frictional torque between the pulley sheaves and the belt, which assist the torque transmission from the primary to secondary pulley. An example of the hydraulic pressure control circuit is depicted in Figure 2, here the hydraulic pump feeds the supply line pressure directly to the secondary pulley. This supply line pressure is controlled through the secondary valve to modulate the pressure according the required clamping force needed for a given load torque. On the other hand, the primary valve regulates the supply line pressure feeding the primary pulley. In practice and under steady-state operation, the regulation of the primary pressure is governed by a 3-D map that relates the primary to secondary pressure ratio with the speed and torque ratios of the CVT.
3. Control Approaches
The main aim of a CVT control is to achieve the desired speed ratio in a fast and accurate manner. Numerous control methodologies have been developed to achieve the desired speed ratio, while improving the efficiency and drivability of the vehicle by means of minimizing the rate of ratio change. Further, CVT control aims at reducing slip by means of clamping force control [3] . Various CVT control methods have been developed including the model-based hydraulic control [4] , fuzzy logic ratio controller [5] , gain scheduled Proportional Integral (PI) controller [6] , and the Proportional Integral Derivative PID-based speed ratio control [7] . Hydraulic control of CVT is one of the widely used control methods for push-belt CVTs that controls the ratio tracking by either the pressure or flow control. This is a complex control system in which the clamp-
![]()
Figure 1. A typical metal push belt type CVT design configuration [3] .
![]()
Figure 2. Schematic diagram for the pulley hydraulic control circuit [3] .
ing forces are controlled such that they are high enough to control slip and low enough to control wear [3] . A flow control system achieves ratio control by controlling the flow of oil to and from the primary actuator. A flow control system does not account for the thrust forces acting on the actuator, and is well suited for simple mechanical control of CVTs. On the other hand, a pressure control system actively controls the primary clamping force, reducing belt slippage. Despite being an easier way of controlling the speed ratio, pressure control systems have not been widely implemented due to the accurate information required about the relation between primary thrust, torque and speed ratio [8] . Development of electronically controlled CVTs has pushed the research into pressure control systems into a wider prominence.
4. Model Development
There are many modeling approaches that can be adopted, but every methodology has its own requirements and objectives. The first method is the multi-body approach [9] . This method is used to analyze and study the different dynamical behaviors of the system under different loading conditions, such as slip, variator deformations, misalignment, and the Noise, Vibration and Harshness (NVH) characteristics of the vehicle. The main issues concerning this approach are the high computational requirements and the large number of states, which make it impractical to implement a controller with such a high fidelity model. The second approach is based on experimental data, [10] and [11] , that relates the variators primary to secondary clamping force ratio, which is a nonlinear relation that depends on the input torque and the gear ratio. This method is the most commonly used in the initial stages of controller designs, due to its simplicity and reliability, but the main drawback is the experimental work needed to generate the look-up tables that represent the primary to secondary variator force ratio. The third approach, which is adopted in this study, is the quasi-static approach, which is a popular tool to estimate the fuel economy and validating the control strategy. This method is based on the idea of backward vehicle simulation. This method does not take into account the transient behavior but it demonstrates the effectiveness of the control strategy on fuel economy, vehicle performance and drivability attributes. The model developed achieves clamping force control by controlling the pressure in the hydraulic system. This, in turn, controls the CVT gear ratio needed to achieve the desired speed and improves the fuel economy of the vehicle. A few assumptions are made in order to simplify the designed model. These include the assumption that the engine is always coupled to the transmission and thus the dynamics of the ratio change in the CVT affect the change in operating point of the engine. The overall vehicle systems model is adopted from [12] , Figure 3. The complete vehicle model includes a driver (PID controller) that receives the error relative to the cycle speed and outputs the throttle and brake demands accordingly. The model does not represent the wheel slip, and thus it can pass the wheel speed backward to the other powertrain models, which output the engine speed forward. The vehicle block shown below, includes all the resistance forces acting on the vehicle.
4.1. Overall Vehicle Model
The overall vehicle model, Figure 3, consists of driver, engine, CVT, final drive, wheel and vehicle road load subsystems. The driver model is represented by a simple PID tuner that minimizes the difference between the actual vehicle speed and desired test cycle velocity profile. Based on this difference, the driver model either outputs a throttle command to control the engine torque or a brake pedal command that applies a braking torque to the wheels. The Engine model receives engine speed according to the overall driveline gear ratio and the throttle command and accordingly outputs the engine torque, Figure 4. Additionally, based on the engine speed and throttle command, an optimal or target CVT gear ratio is determined, this is discussed in the following section. As a result, the CVT hydraulic controller will adjust the pressure in order in order to reduce the difference between the actual and target CVT gear ratios.
4.2. Engine Model
The engine is modeled using an existing 3 L engine map to obtain a target gear ratio and a torque for given secondary pulley speed and throttle position. To derive the target
![]()
Figure 3. A block diagram showing the full system model, including driver, engine, CVT and vehicle road load models.
![]()
Figure 4. Engine model is developed in Simulink platform to represent the engine torque as a function of speed and throttle demand.
gear ratio and torque output of the engine, a specific ratio set point strategy known as optimal operation line tracking is used.
The ratio set point determines the engine efficiency and also affects the drivability of the car. Thus careful consideration must be given to set the operating points depending on various road load demands and speeds. In this study, the ratios set points are chosen with the aim of minimizing fuel consumption. This is known as Optimal Operation Line Tracking (OOL Tracking). Although it optimizes fuel economy, it gives rather poor performance due to the limitation of the torque [4] . To set the ratio points first an S-Function is utilized, Figure 5, that optimizes the torques at each power line. This is done by using a cost function that minimizes fuel consumption [12] , as following:
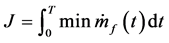 (1)
(1)
Subject to
・ 
・ 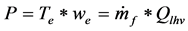
・ 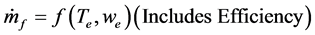
・ 
・ 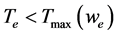
By using the above-explained cost function; an optimum throttle versus speed map is derived by fitting a new line on the optimal operation line, Figure 6. This is done in order to achieve smooth drivability [13] .
 (2)
(2)
Now using a constantly increasing velocity profile and the final drive ratio, the required secondary pulley speed for each vehicle velocity is calculated. Using this secondary pulley speed and optimal throttle for each speed and secondary pulley speed a map of the optimal CVT gear ratio is calculated, Figure 7. The system constraint is (Minimum Ratio £ CVT Ratio £ Maximum Ratio).
![]()
Figure 5. Cost function evaluation using Matlab/Simulink S-function to determine the optimal engine torque.
![]()
Figure 6. The optimal engine operating line (OOL) that minimizes the fuel consumption as a function of engine throttle and speed.
![]()
Figure 7. Optimal CVT ratio map as a function of throttle demand and engine speed.
4.3. CVT Model
The main components that change the gear ratio are the variators (pulleys) radii, as shown in Figure 8. If the secondary variator is displaced by ( ), then the primary variator will be displaced equally and oppositely by (
), then the primary variator will be displaced equally and oppositely by (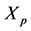 ), leading to modified variator radii and thus modified gear ratio. Assuming the total push-belt length is constant, the kinematics of the two variators are described by the nonlinear equations as following:
), leading to modified variator radii and thus modified gear ratio. Assuming the total push-belt length is constant, the kinematics of the two variators are described by the nonlinear equations as following:
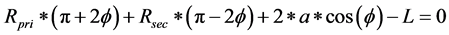 (3)
(3)
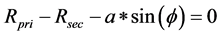 (4)
(4)
![]() (5)
(5)
Here![]() ,
, ![]() and
and ![]() are the primary radius, secondary radius and the gear ratio respectively.
are the primary radius, secondary radius and the gear ratio respectively. ![]() is the belt entrance angle, a is the center distance between the variators and L is the total belt length. Equation (3), can be derived by summing the belt lengths over the pulleys and in the free sections, which is equal to the total belt length (L). Additionally, Equations ((4) and (5)) describe the constant pulleys center-to-center distance (a) as a function of the angle (
is the belt entrance angle, a is the center distance between the variators and L is the total belt length. Equation (3), can be derived by summing the belt lengths over the pulleys and in the free sections, which is equal to the total belt length (L). Additionally, Equations ((4) and (5)) describe the constant pulleys center-to-center distance (a) as a function of the angle (![]() ) and the pulleys gear ratio, respectively. Regarding the clamping force acting on the variator, this force between the belt and the variator surface that is represented by:
) and the pulleys gear ratio, respectively. Regarding the clamping force acting on the variator, this force between the belt and the variator surface that is represented by:
![]() (6)
(6)
The engine torque is given by T. Here it is assumed that the secondary clamping force is equal to the primary, without loss of generality, this assumption is adequate for the control problem objective, but it would be more accurate if the ratio between the primary and secondary force experimental data is available.
Thus, the forces acting on the variator including the hydraulic actuation force is given as:
![]() (7)
(7)
Here m is the variator mass, P is the hydraulic pressure, K is the return spring stiffness, C is the damping coefficient and x is the variator displacement. Since the hydraulic circuit details are hard to obtain, and due to the fact, that the pressure rise and drop are linearly related to the solenoid input current, the pressure dynamics could be
represented as a first order transfer function, with a time constant of 5 ms.
5. Hydraulic Control Strategy
The real CVT utilizes a current input to the hydraulic solenoid, and this is the main control input adopted in this model since the pressure is related to the variator displacement and accordingly to the variator radii and gear ratio. In the model it is assumed that both variators are displaced equally in opposite directions. From Figure 9, the primary variator displacement is related to the radius according to:
![]() (8)
(8)
Since both variators are displaced equally, the secondary variator radius is:
![]() (9)
(9)
These two relations lead to a geometric gear ratio given by:
![]() (10)
(10)
The objective of the proposed controller is to control the variator position according to a desired gear ratio command evaluated by the engine controller. The system has three states (pressure, variator position and velocity), and one output which is the actual variator position (gear ratio), Figure 10. From the model it is found that, the system is stable and thus a PID controller should meet the control objectives such as fast response time (settling time) and minimized steady state error (to prevent gear ratio hunting or speed oscillations).
6. Results
A complete vehicle simulator including the pressure controller was constructed in Matlab-Simulink. The model was subjected to two driving cycles, namely Federal Urban Driving Schedule (FUDS) and Federal Highway Driving Schedule (FHDS), to evaluate the CVT and controller performances.
Figure 11 shows the vehicle actual velocity and the cycle target velocity. The results matches well with the target velocity meaning both the driver model and the available power were both capable of meeting the cycle-required load. Regarding the controller, Figure 12 depicts the target gear ratio needed to minimize the fuel consumption, as introduced in the model development section, and the actual gear ratio archived by the
![]()
Figure 10. Variator’s position-hydraulics PID controller.
![]()
Figure 11. Vehicle velocity tracking during test cycles.
CVT pressure controller, both the desired and the actual are in good agreement. Noticing that the FUDS is mostly operating at higher gear ratios while the FHDS is at the lower gear ratios, this is due to nature of the driving cycle load and acceleration demands.
Due to the higher torque demands during FUDS cycle, the clamping force required is expected to be high due to proportional relation in Equation (6). This can be observed in Figure 13, which shows a higher required clamping force during FUDS than FHDS, therefore, it is most likely that the CVT parasitic load due to the hydraulic requirements, during FUDS cycles or any similar driving behavior would be high.
Figure 14 shows the operating points of the engine during the two driving cycles, it is clear that the CVT ratio controller is following the optimum operating line and it keeping the engine operating at the most efficient contours, this is regardless to the type of the driving cycle. However, during FUDS cycle, the engine operates at higher torque and speeds due to aggressive nature of the cycle velocity profile, while in the FHDS the figure shows fewer variations in the operating point due to the slowly varying speed profile of this cycle.
7. Conclusion
Optimum operating line tracking strategy was implemented to achieve the optimum CVT ratio by implementing a pressure controller. The pressure controller uses a typical
![]()
Figure 14. Engine operating points during test cycles.
PID that was tuned to provide a fast settling time and minimized steady-state error to present engine speed oscillations. The CVT pulleys were modeled as a mechanical hard stop, which represents the interaction between the CVT belt clamping force and the hydraulic pressure. The controller was implemented in a full vehicle model that includes the engine, CVT, road load and a PID-type driver model. Two driving cycles were simulated and the results showed a good agreement in tracking the required velocity profiles as well as in tracking the optimum operating points.
Nomenclature
![]() = Power requested by the driver.
= Power requested by the driver.
![]() = Engine torque.
= Engine torque.
![]() = Fuel mass flow rate.
= Fuel mass flow rate.
![]() = Engine speed.
= Engine speed.
![]() = Fuel’s lower heating value.
= Fuel’s lower heating value.
![]() = Radius of the primary and secondary pulleys.
= Radius of the primary and secondary pulleys.
![]() = Exit and entrance angle of the belt.
= Exit and entrance angle of the belt.
![]() = Pulleys center to center distance.
= Pulleys center to center distance.
![]() = Total belt length.
= Total belt length.
![]() = Radii ratio.
= Radii ratio.
![]() = Clamping force.
= Clamping force.
![]() = Pulley half groove angle.
= Pulley half groove angle.
![]() = Coefficient of friction.
= Coefficient of friction.
![]() = Variator mass.
= Variator mass.
![]() = Variator displacement.
= Variator displacement.
![]() = Hydraulic pressure.
= Hydraulic pressure.
![]() = Variator piston area.
= Variator piston area.
![]() = Spring stiffness.
= Spring stiffness.
![]() = Damping coefficient.
= Damping coefficient.
![]()
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact mme@scirp.org