The Effect of Nanometer Size Effect on the Optical Property of Metallic Wire Grid ()
1. Introduction
The metallic wire grid has also been applied to a broad range of optical systems, such as WGPs, transparent metal electrodes for organic solar cells and organic light-emitting diodes. Now, many papers were focused on the investigation of the polarized property of metallic wire grid [1] - [7] . But few papers reported the theoretical optical property of metallic wire grid because the metallic wire grid always has large extinction coefficient. For example, Vadym Apalkov [8] studied the interaction between an H-wave and a thin metal film. They had calculated reflectance coefficients of a thin metal layer in the case of different values of the incidence angle. Utkin A. I. [9] analyzed the dependence of coefficients of transmission, reflection and absorption of an electromagnetic wave on the thickness of skin in thin metallic films layer. Latyshev A. V. [10] analyzed the functions of transmission, reflection, and absorption coefficients with the angle of incidence of the electromagnetic wave, thickness of the layer. Then, these papers do not consider the effect of the width of metal film on these optical prompters
The optical property of the metal strongly depends on the free path of the free electronic. In this paper, one simple model is given to investigate the effect of width of metallic wire grid on both the mean free path and the corresponding conductivity. Further, we also gave one relationship between the width of metallic wire grid and the reflectivity. Finally, we give the theoretical simulation and discussions.
2. Theory
The structure model of one metallic wire grid is given in Figure 1, in which the metallic wire grid of cuboids with the same width and height are deposited on the glass substrates.
In order to study the effect of width on the electronic mean free path, we present one ball with the diameter of mean free path, in which the electronic can freely move Figure 2 is a model when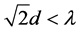
, 
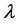is defined as the mean free path, d is the width and height of metallic wire grid, respectively. Figure 3 is another model when
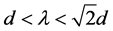. In Figure 2 and Figure 3, the overlapping region between the free path ball and metallic wire grid is the space where the electronic can freely move.
For the mean free path λ of electron in material, the volume of free path ball is that
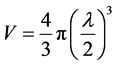(1)
Here, λ is the mean free path in metallic media. For the model mentioned above, the volume of free path in metallic wire grid is, respectively,
(2)
Here, d is the width of wire grid. In order to the study the effect degree of the width of metallic wire grid on the mean free path, we define γ as one corrected factor. Thus, we have
![]()
Figure 1. The structure model of metallic wire grid.
![]()
(1) (2)
Figure 2. The mode of free path affected by the width metallic wire grid (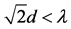
). Here (1) is a front view, (2) is a lateral view.
![]()
Figure 3. The mode of free path affected by the width of metallic wire grid (
). Here (1) is front view, (2) is a lateral view.
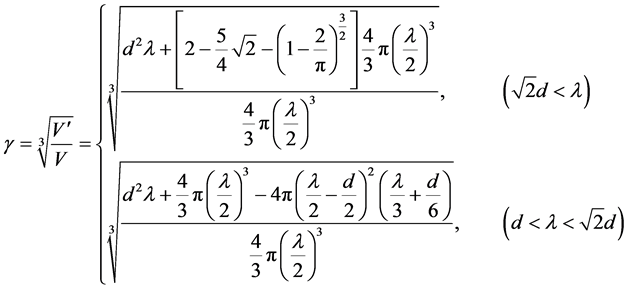(3)
The substitution of (3) into (2) produces one expression to calculate the mean free path in wire grid, which is
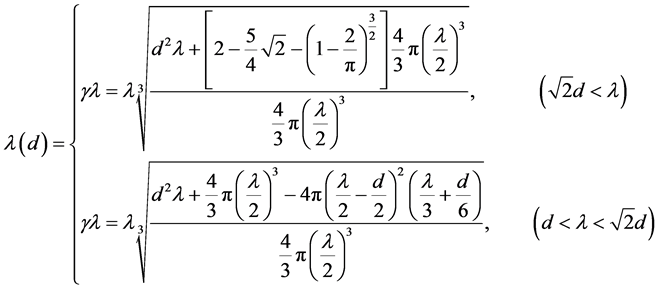(4)
Here, 
is the free path in material,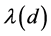 
is the corrected mean free path in wire grid.
3. Calculation of Reflectance
Putting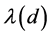 
into the conductivity formula of continuous metallic film, we have
(5)
here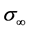 
is the conductivity of normal metal material, σ is the conductivity of corresponding metallic wire grid, ζ is related to the electron pen trance in length.
For the metal (Ag) wire grid, the parameters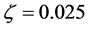
, ![]()
, ![]()
, ![]()
, respectively. The simulation cure of (5) is given in Figure 4.
Seeing from Figure 4, the conductivity increases as the width of metallic wire grid increases. For example, it is obvious that the conductivity at ![]()
is larger than that at![]()
. Hence, we deduce that the conductivity depends on the width of metallic wire grid.
According to Maxwell’s equation, the relationship of refractive index with the conductivity is
![]()
(6)
Here
![]()
, ![]()
![]()
Figure 4. The relation cure of conductivity with the width of metallic wire grid.
here ![]()
is the real part of refractive index, k is the imaginary part. According to the reflectivity formulation, we have
![]()
(7)
Equation (7) can clearly describe the relationship between the reflectance and with the width of metallic wire grid. It could be used to calculate the reflectance of wire grid. For example, When the light wavelength is equal to 632 nm and 532 nm, respectively, the corresponding relative dielectric constant of metal (Ag)![]()
, respectively. For the wire grid of Ag, the parameters is![]()
, ![]()
, ![]()
and![]()
, respectively. Based on these parameters, we give the two cure (seeing Figure 2), which corresponds to the reflectance of metallic wire grid at the wavelength of 532 nm and 632 nm, respectively. Because the material optical parameters of other wavelength have not been obtained, we could not give the corresponding cure.
Seeing from Figure 5, the reflectance would increases when the width of metallic wire grid increases. For example, the reflectance is about 72% at![]()
, and the reflectance of 73% at ![]()
when the wavelength is 532 nm. For the wavelength of 632 nm, the reflectance is about 69% at![]()
, and the reflectance of
71.5% at![]()
. These results demonstrate the reflectance is different when the width of metallic wire grid is different.
4. Conclusion
This paper studied the influence of metal wire grid width on electron mean free path. The simple physical mode of electron mean free path affected by grid width is given. We give one corrected expression to calculate the conductivity of metallic wire grid. The theoretical simulation shows that the conductivity increases as the width of metallic wire grid increases. Further, we also investigated the relationship between the width of metal wire grid and the reflectance, and gave one corrected expression. Our simulation demonstrates that the reflectance increases as the width of metallic wire grid increases, which is very valuable to investigate the optical property of wire grid.