1. Introduction
Duadic codes form a class of cyclic codes that generalizes quadratic residue codes from prime to composite lengths. While initially quadratic residue codes were studied within the confines of finite fields, there have been recent developments on quadratic residue codes over some special rings. Pless and Qian [1] studied quadratic residue codes over , Chiu et al. [2] extended the ideas to the ring
, Chiu et al. [2] extended the ideas to the ring 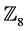 and Taeri [3] considered QR- codes over
and Taeri [3] considered QR- codes over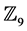 . Kaya et al. [4] and Zhang et al. [5] studied quadratic residue codes over
. Kaya et al. [4] and Zhang et al. [5] studied quadratic residue codes over
 where p is an odd prime. Kaya et al. [6] studied quadratic residue codes over
where p is an odd prime. Kaya et al. [6] studied quadratic residue codes over
 whereas Liu et al. [7] studied them over non-local ring
whereas Liu et al. [7] studied them over non-local ring
 where
where  and p is an odd prime. The authors [8] along with Kathuria extended their results over the ring
and p is an odd prime. The authors [8] along with Kathuria extended their results over the ring 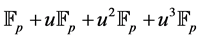 where
where 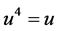
and![]() . In [9] the authors studied quadratic residue codes and their
. In [9] the authors studied quadratic residue codes and their
extensions over the ring ![]() where
where ![]() and p is a prime satisfying
and p is a prime satisfying ![]() generalizing all the previous results.
generalizing all the previous results.
There are duadic codes which are not quadratic residue codes, but they have properties similar to those of quadratic residue codes. In this paper we extend our
results of [9] to duadic codes over the ring![]() , where
, where
![]() , q is a prime power congruent to 1 modulo
, q is a prime power congruent to 1 modulo![]() . The Gray map defined in
. The Gray map defined in
[9] is also extended from ![]() which preserves linearity and in some special
which preserves linearity and in some special
cases preserves self duality. The Gray images of extensions of duadic codes over the ring ![]() lead to construction of self-dual, formally self-dual and self-orthogonal codes. We give some examples of duadic but non quadratic residue codes which give rise to a [40,20,6] self-dual code over
lead to construction of self-dual, formally self-dual and self-orthogonal codes. We give some examples of duadic but non quadratic residue codes which give rise to a [40,20,6] self-dual code over![]() , a [27,12,6] self orthogonal code over
, a [27,12,6] self orthogonal code over![]() , a [30,12,8] self-orthogonal code over
, a [30,12,8] self-orthogonal code over ![]() and a formally self-dual [24,12,6] code over
and a formally self-dual [24,12,6] code over![]() .
.
The paper is organized as follows: In Section 2, we recall duadic codes of length n
over ![]() and state some of their properties. In Section 3, we study the ring
and state some of their properties. In Section 3, we study the ring
![]() , cyclic codes over ring
, cyclic codes over ring ![]() and define the Gray map
and define the Gray map![]() . In Section 4, we study duadic codes over
. In Section 4, we study duadic codes over![]() , their extensions and give some of their properties. We also give some examples to illustrate our results.
, their extensions and give some of their properties. We also give some examples to illustrate our results.
2. Duadic Codes over ![]() and Their Properties
and Their Properties
In this section we give the definition of duadic codes and state some of their properties. Before that we need some preliminary notations and results.
A cyclic code ![]() of length n over
of length n over ![]() can be regarded as an ideal of the ring
can be regarded as an ideal of the ring
![]() . It has a unique idempotent generator
. It has a unique idempotent generator![]() .
.
Let![]() . The
. The ![]() cyclic code
cyclic code ![]() has generating
has generating
idempotent![]() , its dual is the repetition code with generating idempotent
, its dual is the repetition code with generating idempotent![]() .
.
A polynomial ![]() is called even like if
is called even like if ![]() otherwise it is
otherwise it is
called odd like. A code ![]() is called even like (odd like) if all its codewords are even like (odd like). For
is called even like (odd like) if all its codewords are even like (odd like). For![]() ,
, ![]() defined as
defined as ![]() is called a multiplier where
is called a multiplier where![]() . It is extended on
. It is extended on ![]() by defining
by defining
![]() .
.
Suppose n is odd, ![]() and
and![]() , where
, where
(i)![]() ,
, ![]() are union of q-cyclotomic cosets mod n.
are union of q-cyclotomic cosets mod n.
(ii) ![]()
(iii) There exists a multiplier![]() ,
, ![]() such that
such that ![]() and
and![]() .
.
Then codes ![]() and
and ![]() having
having ![]() and
and ![]() as defining sets are called a pair of odd like duadic codes and codes
as defining sets are called a pair of odd like duadic codes and codes ![]() and
and ![]() having
having ![]() and
and ![]() as def- ining sets are called a pair of even like duadic codes.
as def- ining sets are called a pair of even like duadic codes.
It is known that duadic codes exist if and only if q is a square mod n.
There is an equivalent definition of duadic codes in terms of idempotents. (For details see Huffman and Pless [10] , Chapter 6).
Let ![]() and
and ![]() be two even like idempotents with
be two even like idempotents with ![]() and
and![]() . The codes
. The codes ![]() and
and ![]() form a pair of even like duadic codes if and only if
form a pair of even like duadic codes if and only if
(1) the idempotents satisfy
![]()
(2) There is a multiplier ![]() such that
such that
![]() and
and![]() .
.
i.e. ![]() and
and ![]()
Associated to ![]() and
and ![]() there is a pair of odd like duadic codes
there is a pair of odd like duadic codes ![]() and
and ![]() generated by idempotents
generated by idempotents ![]() and
and ![]() respectively, where
respectively, where![]() ,
, ![]()
If (1) and (2) hold we say that ![]() gives a splitting for even like duadic codes
gives a splitting for even like duadic codes ![]() and
and ![]() or for the odd like duadic codes
or for the odd like duadic codes ![]() and
and![]() .
.
Lemma 1: Let ![]() and
and ![]() be a pair of even-like duadic codes of length n over
be a pair of even-like duadic codes of length n over![]() . Suppose
. Suppose ![]() gives the splitting for
gives the splitting for ![]() and
and![]() . Let
. Let ![]() and
and ![]() be the associated odd-like duadic codes. Then:
be the associated odd-like duadic codes. Then:
(i) ![]()
(ii) ![]() and
and![]() ,
,
(iii) ![]() is even like subcode of
is even like subcode of ![]() for
for![]() ,
,
(iv) ![]() and
and![]() , and
, and
(v) ![]() for
for![]() .
.
This is part of Theorem 6.1.3 of [10] .
Lemma 2: Let ![]() and
and ![]() be a pair of even-like duadic codes over
be a pair of even-like duadic codes over ![]() with
with ![]() and
and ![]() the associated pair of odd-like duadic codes.
the associated pair of odd-like duadic codes.
(i) If ![]() and
and ![]()
then ![]() and
and![]() .
.
(ii) If ![]() and
and ![]()
then ![]() and
and ![]()
Proof follows from Theorems 6.4.2 and 6.4.3 of [10] .
Lemma 3:![]() ,
, ![]() ,
, ![]() ,
,![]() . Further
. Further ![]() and
and![]() .
.
Proof follows immediately from the definition and Lemma 1.
3. Cyclic Codes over the Ring R and the Gray Map
Let q be a prime power,![]() . Throughout the paper,
. Throughout the paper, ![]() denotes the commutative ring
denotes the commutative ring![]() , where
, where![]() ,
, ![]() is a natural number and
is a natural number and![]() .
. ![]() is a ring of size
is a ring of size ![]() and characteristic p. For a primitive element
and characteristic p. For a primitive element ![]() of
of![]() , take
, take![]() , so that
, so that ![]() and
and![]() . Let
. Let ![]() denote the following elements of
denote the following elements of![]() :
:
![]() (1)
(1)
A simple calculation shows that
![]() (2)
(2)
The decomposition theorem of ring theory tells us that![]() .
.
For a linear code ![]() of length n over the ring
of length n over the ring![]() , let
, let
![]() .
.
Then ![]() are linear codes of length n over
are linear codes of length n over![]() ,
, ![]() and
and![]() . For a code
. For a code ![]() over
over![]() , the dual code
, the dual code ![]() is defined as
is defined as
![]() where
where ![]() denotes the usual Euclidean inner
denotes the usual Euclidean inner
product. ![]() is self-dual if
is self-dual if ![]() and self-orthogonal if
and self-orthogonal if![]() . A code
. A code ![]() is called formally self-dual if
is called formally self-dual if ![]() and
and ![]() have the same weight distribution.
have the same weight distribution.
The following result is a simple generalization of a result of [7] .
Theorem 1: Let ![]() be a linear code of length n over
be a linear code of length n over![]() . Then
. Then
(i) ![]() is cyclic over
is cyclic over ![]() if and only if
if and only if ![]() are cyclic over
are cyclic over![]() .
.
(ii) If![]() ,
, ![]() , then
, then
![]() where
where ![]() and
and![]() .
.
(iii) Further![]() .
.
(iv) Suppose that ![]() Let
Let ![]() then
then![]() .
.
(v) ![]()
(vi) ![]() where
where![]() , where
, where ![]() is the reciprocal polynomial of
is the reciprocal polynomial of ![]()
(vii)![]() .
.
The following is a well known result :
Lemma 4: (i) Let C be a cyclic code of length n over a finite ring S generated by the idempotent E in ![]() then
then ![]() is generated by the idempotent
is generated by the idempotent![]() .
.
(ii) Let C and D be cyclic codes of length n over a finite ring S generated by the idem-
potents ![]() in
in ![]() then
then ![]() and
and ![]() are generated by the ide-
are generated by the ide-
mpotents ![]() and
and ![]() respectively.
respectively.
Let the Gray map ![]() be given by
be given by
![]()
where M is an ![]() nonsingular matrix of Vandermonde determinant
nonsingular matrix of Vandermonde determinant ![]() and V is any nonsingular matrix over
and V is any nonsingular matrix over ![]() of order
of order![]() . This map can be extended from
. This map can be extended from ![]() to
to ![]() component wise.
component wise.
Let the Gray weight of an element ![]() be
be![]() , the Hamming weight of
, the Hamming weight of![]() . The Gray weight of a codeword
. The Gray weight of a codeword ![]() is defined
is defined
as![]() . For any two elements
. For any two elements
![]() , the Gray distance
, the Gray distance ![]() is given by
is given by![]() .
.
Theorem 2. The Gray map ![]() is an
is an ![]() -linear, one to one and onto map. It is also
-linear, one to one and onto map. It is also
distance preserving map from (![]() , Gray distance
, Gray distance![]() ) to (
) to (![]() , Hamming distance).
, Hamming distance).
Further if the matrix V satisfies![]() ,
, ![]() , where
, where ![]() denotes the transpose
denotes the transpose
of the matrix V, then the Gray image ![]() of a self-dual code
of a self-dual code ![]() over
over ![]() is a self-
is a self-
dual code in![]() .
.
The proof follows exactly on the same lines as the proof of Theorem 2 of [9] . The only difference is that here q is an arbitrary prime power and not just an odd prime. For the sake of completeness of the result we reproduce the proof here.
Proof. The first two assertions hold as ![]() is an invertible matrix over
is an invertible matrix over![]() .
.
Let now![]() ,
, ![]() , satisfying
, satisfying![]() . So that
. So that
![]() (3)
(3)
Let ![]() be a self-dual code over
be a self-dual code over![]() . Let
. Let ![]() where
where ![]() and
and![]() . Then
. Then
![]()
implies that (comparing the coefficients of ![]() on both sides)
on both sides)
![]() (4)
(4)
![]() (5)
(5)
for each r, ![]()
For convenience we call ![]() and
and![]() . Then
. Then
![]()
Similarly
![]()
Using (2), we find that
![]()
Now
![]()
Using (3) and (4), one can check that each ![]() is zero, which proves the result.
is zero, which proves the result.
4. Duadic Codes over the Ring R
We now define duadic codes over the ring ![]() in terms of their idempotent generators. Let
in terms of their idempotent generators. Let ![]() denote the ring
denote the ring![]() . Using the properties (2) of idempotents
. Using the properties (2) of idempotents![]() , we have
, we have
Lemma 5: Let ![]() and
and ![]() be idempotents as defined in
be idempotents as defined in
(1). Then for ![]() and for any tuple
and for any tuple ![]() of odd-like idem-
of odd-like idem-
potents not all equal and for any tuple ![]() of even-like idempotents not all equal,
of even-like idempotents not all equal, ![]() and
and ![]() are respectively odd-like and even-like idempotents in the ring
are respectively odd-like and even-like idempotents in the ring![]() .
.
Throughout the paper we assume that q is a square mod n so that duadic codes of
length n over ![]() exist. The construction and the properties of duadic codes over the ring
exist. The construction and the properties of duadic codes over the ring ![]() is similar to that of quadratic residue codes over the ring
is similar to that of quadratic residue codes over the ring![]() , where
, where ![]() given in [9] . We denote the set
given in [9] . We denote the set ![]() by
by![]() . For each
. For each![]() , let
, let ![]() denote the odd-like idempotent of the ring
denote the odd-like idempotent of the ring ![]() in which
in which ![]() occurs at the ith place and
occurs at the ith place and ![]() occurs at the remaining
occurs at the remaining ![]() places i.e.
places i.e.
![]() (6)
(6)
For![]() ,
, ![]() let
let ![]() denote the odd-like idempotent in which
denote the odd-like idempotent in which ![]() occ- urs at the
occ- urs at the ![]() and
and ![]() places and
places and ![]() occurs at the remaining
occurs at the remaining ![]() places i.e.
places i.e.
![]() (7)
(7)
In the same way, for![]() ,
, ![]() let
let ![]() denote the odd-like idempotent
denote the odd-like idempotent
![]() (8)
(8)
For![]() ,
, ![]() , where
, where ![]() let the corresponding odd-like idempotents be
let the corresponding odd-like idempotents be
![]() (9)
(9)
![]() (10)
(10)
Similarly we define even-like idempotents for ![]() and
and![]() ,
, ![]() ,
,
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
Let ![]() denote the odd-like duadic codes and
denote the odd-like duadic codes and ![]() denote the even-like duadic codes over
denote the even-like duadic codes over ![]() generated by the corresponding idempotents, i.e.
generated by the corresponding idempotents, i.e.
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,![]() .
.
Theorem 3: Let![]() , Then for
, Then for![]() ,
, ![]() is equivalent to
is equivalent to ![]() and
and ![]() is equivalent to
is equivalent to![]() . For
. For![]() ,
, ![]() ,
, ![]() is equivalent to
is equivalent to![]() , and
, and ![]() is equivalent to
is equivalent to![]() . Further there are
. Further there are
![]() inequivalent odd-like duadic codes and
inequivalent odd-like duadic codes and ![]() inequivalent even-like duadic codes over the ring
inequivalent even-like duadic codes over the ring![]() .
.
Proof: Let the multiplier ![]() give splitting of
give splitting of ![]() and
and ![]() or of
or of ![]() and
and![]() . Then
. Then![]() ,
, ![]() ,
, ![]() ,
, ![]() and so
and so
![]() ,
, ![]() ,
, ![]() ,
,![]() . This proves that
. This proves that ![]()
![]() ,
, ![]() , and
, and![]() .
.
Note that![]() ,
, ![]() ,
, ![]() ,
,![]() . Therefore
. Therefore
![]() (15)
(15)
![]() (16)
(16)
For a given positive integer k, the number of choices of the subsets ![]() of
of ![]() is
is![]() .
.
Let m be even first. Then![]() . Using (15) and
. Using (15) and
(16), we find that the number of inequivalent odd-like or even-like duadic-codes is
![]() . If m is odd the number of inequiv- alent odd-like or even-like duadic codes is
. If m is odd the number of inequiv- alent odd-like or even-like duadic codes is![]() .
.
Let ![]() denote the greatest integer
denote the greatest integer![]() . we have
. we have ![]() when m is even and
when m is even and ![]() when m is odd.
when m is odd.
Theorem 4: If![]() , then for subsets
, then for subsets ![]() of
of ![]() with cardinality k,
with cardinality k, ![]() , the following assertions hold for duadic codes over
, the following assertions hold for duadic codes over![]() .
.
(i) ![]()
(ii) ![]()
(iii) ![]()
(iv) ![]()
(v) ![]()
(vi) ![]()
(vii) ![]()
Proof: From the relations (2),(6)-(14) we see that![]() ,
, ![]() ,
, ![]() and
and![]() . Therefore by Lemmas 1 and 4,
. Therefore by Lemmas 1 and 4, ![]() , and
, and![]() ;
;![]() , and
, and![]() . This proves (i)-(iv).
. This proves (i)-(iv).
Using that ![]() and
and ![]() from Lemma 3 and noting that
from Lemma 3 and noting that ![]() we find that
we find that![]() .
.
Similarly using ![]() and
and ![]() from Lemma 3, we see that
from Lemma 3, we see that![]() .
.
Therefore ![]() and
and![]() . This proves (v) and (vi).
. This proves (v) and (vi).
Finally for![]() , we have
, we have
![]()
it being a repetition code over![]() . Therefore
. Therefore
![]()
This gives![]() . Now we find that
. Now we find that
![]()
since![]() . This gives
. This gives![]() .
.
Theorem 5 : If![]() , and if
, and if![]() ,
, ![]() then for each possible tuple
then for each possible tuple![]() , the following assertions hold for duadic codes over
, the following assertions hold for duadic codes over![]() .
.
(i) ![]()
(ii) ![]() is self orthogonal.
is self orthogonal.
Proof: By using Lemma 2 and Lemma 4, we have ![]() so
so![]() . Similarly
. Similarly![]() . For
. For ![]()
![]() . Now result (i) follows from Lemma 4. Using (vi) of Theorem 4, we have
. Now result (i) follows from Lemma 4. Using (vi) of Theorem 4, we have![]() . Therefore
. Therefore ![]() is self orthogonal.
is self orthogonal.
Similarly we get
Theorem 6 : If ![]() and
and![]() ,
, ![]() then for all possible choices of
then for all possible choices of![]() , the following assertions hold for duadic codes over
, the following assertions hold for duadic codes over![]() .
.
(i) ![]()
(ii) ![]()
The extended duadic codes over ![]() are formed in the same way
are formed in the same way
as the extended duadic codes over ![]() are formed. See Theorem 6.4.12 of [10] .
are formed. See Theorem 6.4.12 of [10] .
Consider the equation
![]() (17)
(17)
This equation has a solution ![]() in
in ![]() if and only if n and −1 are both squares or both non squares in
if and only if n and −1 are both squares or both non squares in ![]() (see [10] , Chapter 6).
(see [10] , Chapter 6).
Theorem 7: Suppose there exist a ![]() in
in ![]() satisfying Equation (17). If
satisfying Equation (17). If![]() ,
, ![]() then for all possible choices of
then for all possible choices of![]() , the extended duadic codes
, the extended duadic codes ![]() of length
of length ![]() are self-dual.
are self-dual.
Proof: As![]() , by Theorem 4, let
, by Theorem 4, let ![]() be the exten- ded duadic code over
be the exten- ded duadic code over ![]() generated by
generated by
![]()
where ![]() is a generator matrix for the even-like duadic code
is a generator matrix for the even-like duadic code![]() . The row above the matrix shows the column labeling by
. The row above the matrix shows the column labeling by![]() . Since the all one vector belongs to
. Since the all one vector belongs to ![]() and its dual
and its dual ![]() is equal to
is equal to![]() , the last row of
, the last row of ![]() is orthogonal to all the previous rows of
is orthogonal to all the previous rows of![]() . The last row is orthog- onal to itself also as
. The last row is orthog- onal to itself also as ![]() in
in![]() . Further as
. Further as ![]() is self orthogonal by Theorem 5, we find that the code
is self orthogonal by Theorem 5, we find that the code ![]() is self orthogonal. Now the result foll-
is self orthogonal. Now the result foll-
ows from the fact that![]() .
.
Theorem 8: Suppose there exists a ![]() in
in ![]() satisfying Equation (17). If
satisfying Equation (17). If![]() ,
, ![]() then for all possible choices of
then for all possible choices of![]() , the extended duadic codes satisfy
, the extended duadic codes satisfy![]() .
.
Proof: Let ![]() and
and ![]() be the extended duadic codes over
be the extended duadic codes over ![]() generated by
generated by
![]()
and
![]()
respectively where ![]() is a generator matrix for the duadic code
is a generator matrix for the duadic code ![]() and
and ![]() is a generator matrix for the duadic code
is a generator matrix for the duadic code![]() . Let v denote the all one
. Let v denote the all one
vector of length n. As ![]() and
and![]() , v is orthogonal to all the
, v is orthogonal to all the
rows of![]() . Also
. Also![]() . Further rows of
. Further rows of ![]() are in
are in
![]() , so are orthogonal to rows of
, so are orthogonal to rows of![]() . Therefore all rows of
. Therefore all rows of ![]()
are orthogonal to all the rows of![]() . Hence
. Hence![]() . Now the result follows from comparing their orders.
. Now the result follows from comparing their orders.
Corollary: Let the matrix V taken in the definition of the Gray map ![]() satisfy
satisfy![]() ,
,![]() . If
. If![]() , then for all possible choices of
, then for all possible choices of![]() , the Gray images of extended duadic codes
, the Gray images of extended duadic codes ![]() i.e.
i.e. ![]() are self-dual codes of length
are self-dual codes of length ![]() over
over ![]() and the Gray images of the even-like duadic codes
and the Gray images of the even-like duadic codes
![]() i.e.
i.e. ![]() are self-orthogonal codes of length
are self-orthogonal codes of length ![]() over
over![]() . If
. If![]() , then
, then ![]() are formally self-dual codes of length
are formally self-dual codes of length ![]() over
over![]() .
.
Next we give some examples to illustrate our theory. The minimum distances of all the examples appearing have been computed by the Magma Computational Algebra System.
Example 1: Let![]() ,
, ![]() ,
, ![]() and
and ![]() be a matrix over
be a matrix over ![]()
satisfying![]() . The even like idempotent generators of duadic codes of length 9 over
. The even like idempotent generators of duadic codes of length 9 over ![]() are
are![]() ,
,![]() . Here
. Here![]() ,
,![]() . The Gray image of even like duadic code
. The Gray image of even like duadic code ![]() is a self-orthogonal [27,12,6] code over
is a self-orthogonal [27,12,6] code over![]() . Here there is no
. Here there is no ![]() satisfying Equation (17).
satisfying Equation (17).
Example 2: Let![]() ,
, ![]() ,
, ![]() and
and
![]()
be a matrix over ![]() satisfying
satisfying![]() . The even like idempotent generators of duadic codes of length 9 over
. The even like idempotent generators of duadic codes of length 9 over ![]() are
are![]() ,
,![]() . Here
. Here![]() ,
, ![]() and
and ![]() is a solution of (17). The Gray image
is a solution of (17). The Gray image ![]() of extended duadic code
of extended duadic code ![]() is a self-dual [40,20,6] code over
is a self-dual [40,20,6] code over![]() .
.
Example 3: Let![]() ,
, ![]() ,
, ![]() and
and
![]()
be a matrix over ![]() satisfying
satisfying![]() . The even like idempotent generators of duadic codes of length 5 over
. The even like idempotent generators of duadic codes of length 5 over ![]() are
are![]() ,
,![]() . The Gray image of even like duadic code
. The Gray image of even like duadic code ![]() is a self- orthogonal [30,12,8] code over
is a self- orthogonal [30,12,8] code over![]() .
.
Example 4 : Let![]() ,
, ![]() ,
, ![]() and let a be the primitive element of
and let a be the primitive element of ![]()
![]()
be a matrix over ![]() satisfying
satisfying![]() . The even like idempotent generators of duadic codes of length 5 over
. The even like idempotent generators of duadic codes of length 5 over ![]() are
are![]() ,
,![]() . Here
. Here![]() ,
, ![]() and
and ![]() is a solution of (17). The Gray image
is a solution of (17). The Gray image ![]() of extended duadic code
of extended duadic code ![]() is a formally self-dual [24,12,6] code over
is a formally self-dual [24,12,6] code over![]() .
.