Tightly-Secure Authenticated Key Exchange without NAXOS’ Approach Based on Decision Linear Problem ()

1. Introduction
An Authenticated Key Exchange protocol (AKE) allows two parties to end up with a shared secret key in secure and authenticated manner. The authentication problem deals with restraining adversary that actively controls the communication links used by legitimated parties. They may modify and delete messages in transit, and even inject false one or may control the delays of messages.
In 1993, Bellare and Rogaway [1] provided the first formal treatment of entity authentication and authenticated key distribution appropriate to the distributed environment. In 1998, Bellare, Canetti, Mihir and Krawczyk [2] provided a model for studying session-oriented security protocols. They also introduce the “authenticator” techniques that allow for greatly simplifying the analysis of protocols. Also, they proposed a definition of security of KE protocols rooted in the simulatability approach used to define the security of multiparty computation. In 2002 Canetti and Krawczyk [3] presented their security model which had extended by LaMacchia, Lauter, and Mityagin [4] design and proposed NAXOS protocol which is secure under their model. That model capture attacks resulting from leakage of ephemeral and long-term secret keys, defined by an experiment in which the adversary is given many corruption power for various key exchange sessions and most solve a challenge on a test session. This model doesn’t give an adversary capability to trivially break an AKE protocol.
To acquire eCK security, NAXOS needs that the ephemeral public key X be computed from an exponent result from hashing an ephemeral private key x and the static private key a, more precisely 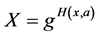 instead of
instead of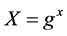 . In this paper generating ephemeral public key as
. In this paper generating ephemeral public key as 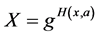 is called NAXOS’s approach. In NAXOS’s approach no one is capable of querying the discrete logarithm of an ephemeral public key X without the pair (
is called NAXOS’s approach. In NAXOS’s approach no one is capable of querying the discrete logarithm of an ephemeral public key X without the pair (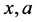 ); thus, the discrete logarithm of X is hidden via an additional random oracle. Using NAXOS' approach many protocols, [5] - [8] were claimed secure in the eCK model under the random oracle assumption. In the standard model, eCK-secure protocols were declared to be secured in the eCK model as Okamoto [9] ; they use pseudo-random functions instead of hash functions.
); thus, the discrete logarithm of X is hidden via an additional random oracle. Using NAXOS' approach many protocols, [5] - [8] were claimed secure in the eCK model under the random oracle assumption. In the standard model, eCK-secure protocols were declared to be secured in the eCK model as Okamoto [9] ; they use pseudo-random functions instead of hash functions.
Motivating Problem. (1) Design AKE-secure protocol without NAXOS trick to achieve two goals: (i) To reduce the risk of leaking the static private key, since the derivation of the ephemeral public key is independent of the static private key. This method is in contrast to protocols that use the NAXOS' approach. (ii) Minimize the utilization of the random oracle, by applying it only to the session key derivation. Kim, Minkyu, Atsushi Fujioka, and Berkant Ustaolu [10] proposed a two strongly secure authenticated key exchange protocols without NAXOS approach, one of their protocol supposed to be secure under the GDH assumption and the other under the CDH assumption in random oracle model. Mohamed et al. [19] designed a protocol without NAXOS approach but secure in RO model, they rely the security of their protocol upon security reduction, and we use in this paper the game sequences tools to fasten the security and give tightly secure security proof. (2) Design AKE-secure protocol secure under Decision Linear Assumption. Boneh, Boyen, and Shacham [11] introduced a decisional assumption, called Linear, intended to take the place of DDH in groups―in particular, bilinear groups [12] ―where DDH is easy. For this setting, the Linear problem has desirable properties, as Boneh, Boyen and Shacham show: it is hard if DDH is hard, but, at least in general groups [13] , remains hard even if DDH is easy.
Contributions. We present a concrete and practical AKE protocol that is eCK secure under Decisional Linear assumption in the random oracle model. Our protocol does not rely on any NAXOS trick that yields a more efficient solution when it is implement- ed with secure device. We give tight proof reducing eCK security of our protocol to break the used cryptographic primitives under random oracle. In our protocol, the ephemeral public key is containing each peers generator, which results in two different discrete logarithm problems with two different generators, which increase hardness for DL’s solver.
In the derivation of the session key, each party will compete shared secret from ephemeral keys and static keys. We fasten the security of this protocol using games sequences tool which gives tight security.
Organization. Section 2 reviews security definitions and states the hard problem. Section 3 gives brief for the eCK model. Section 4 proposes AKE-secure protocol with its security results. Section 5 compares our protocol with other related AKE protocols and shows its efficiency. And finally, we draw the conclusion in Section 6.
2. Preliminaries
In this section, we review security definitions we will use to construct our protocol.
2.1. The Decision Linear Diffie-Hellman Assumption
Let G be a cyclic group of prime order p and along with arbitrary generators 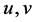 and h where
and h where
 (1)
(1)
consider the following problem:
Decision Linear Problem in G [11] Given 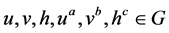 as input, output yes if
as input, output yes if 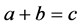 and no otherwise.
and no otherwise.
One can easily show that an algorithm for solving Decision Linear in G gives an algorithm for solving DDH in G. The converse is believed to be false. That is, it is believed that Decision Linear is a hard problem even in bilinear groups where DDH is easy. More precisely, we define the advantage of an algorithm 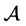 in deciding the Decision Linear problem in G as
in deciding the Decision Linear problem in G as
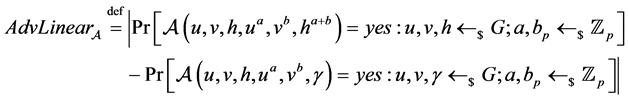 (2)
(2)
The probability is over the uniform random choice of the parameters to , and over the coin tosses of
, and over the coin tosses of . We say that an algorithm
. We say that an algorithm  -decides Decision Linear in G if
-decides Decision Linear in G if  runs in time at most t, and
runs in time at most t, and  is at least
is at least .
.
Definition 2.1. We say that the 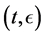 -Decision Linear Assumption (DLIN) holds in G if no t-time algorithm has advantage at least
-Decision Linear Assumption (DLIN) holds in G if no t-time algorithm has advantage at least  in solving the Decision Linear problem in G.
in solving the Decision Linear problem in G.
2.2. Linear Diffie-Hellman
Let ![]() be the discrete logarithm (DL) functions which takes an input
be the discrete logarithm (DL) functions which takes an input ![]() and returns
and returns ![]() such that
such that ![]() and
and![]() . Define the Linear Diffie-Hellman functions
. Define the Linear Diffie-Hellman functions ![]() as
as![]() ,
, ![]() , and Decisional Linear predicate
, and Decisional Linear predicate ![]() as a function which takes an input
as a function which takes an input ![]() and returns 1 if
and returns 1 if
![]() (3)
(3)
or in input ![]() and returns 1 if
and returns 1 if
![]() (4)
(4)
3. Security Model
In this section, eCK model is outlined [18] . An n different parties ![]() running the KE protocol
running the KE protocol ![]() in eCK model. Each party possesses long-term static (private/public) keys including the corresponding certificate issued by the certifying authority. The protocol
in eCK model. Each party possesses long-term static (private/public) keys including the corresponding certificate issued by the certifying authority. The protocol ![]() is executed between two parties
is executed between two parties ![]() and
and ![]() whose static public key are A and B respectively.
whose static public key are A and B respectively. ![]() and
and ![]() will interchange their ephemeral public keys X and Y to obtain the same session key.
will interchange their ephemeral public keys X and Y to obtain the same session key.
Sessions: A party is activated by an outside call or an incoming message to execute the protocol![]() . Each program of executing
. Each program of executing ![]() is modeled as an interactive probabilistic polynomial-time machine. We call a session an invocation of an instance of
is modeled as an interactive probabilistic polynomial-time machine. We call a session an invocation of an instance of ![]() within a party. We assume that
within a party. We assume that ![]() is the session initiator and
is the session initiator and ![]() is the session responder. Then
is the session responder. Then ![]() is activated by the outside call
is activated by the outside call ![]() or the incoming message
or the incoming message![]() . When activated by
. When activated by![]() ,
, ![]() prepares an ephemeral public key X and stores a separate session state which includes all session-specific ephemeral information. The session identifier (denoted by sid) in
prepares an ephemeral public key X and stores a separate session state which includes all session-specific ephemeral information. The session identifier (denoted by sid) in ![]() is initialized with
is initialized with![]() . After
. After ![]() is activated by
is activated by ![]() (receiving an appropriate message from responder), the session identifier is updated to
(receiving an appropriate message from responder), the session identifier is updated to![]() . Similarly, the responder
. Similarly, the responder ![]() is activated by the incoming message
is activated by the incoming message![]() . When activated,
. When activated, ![]() also prepares an ephemeral public key Y and stores a separate session state, and the corresponding session identifier is
also prepares an ephemeral public key Y and stores a separate session state, and the corresponding session identifier is![]() . A
. A ![]() (if it exists) is said to be matching to the session
(if it exists) is said to be matching to the session ![]() or
or![]() . For a session
. For a session![]() ,
, ![]() is called the owner of the session while
is called the owner of the session while ![]() is called the peer of the session. We say sid is complete if there is no symbol “-” in sid.
is called the peer of the session. We say sid is complete if there is no symbol “-” in sid.
Adversaries: The adversary ![]() is also modeled as a probabilistic polynomial-time machine.
is also modeled as a probabilistic polynomial-time machine. ![]() controls the whole communications between parties by sending arbitrary messages to the intended party on behalf of another party and receiving the outgoing message from the communicating parties. In order to capture the possible attacks,
controls the whole communications between parties by sending arbitrary messages to the intended party on behalf of another party and receiving the outgoing message from the communicating parties. In order to capture the possible attacks, ![]() is allowed to make the following queries as well as H queries of (hash) random oracles.
is allowed to make the following queries as well as H queries of (hash) random oracles.
Establish Party (![]() ):
):![]() Registers an arbitrary party
Registers an arbitrary party ![]() not in P, whose static public key is on
not in P, whose static public key is on ![]() s own choice. We call this kind of newly registered parties dishonest (
s own choice. We call this kind of newly registered parties dishonest (![]() totally controls the dishonest parties) while the parties in P are honest. We require that when
totally controls the dishonest parties) while the parties in P are honest. We require that when ![]() makes such query, the certifying authority should verify that the submitted static public key is in the appropriate group (to avoid small subgroup attack) and the proof that
makes such query, the certifying authority should verify that the submitted static public key is in the appropriate group (to avoid small subgroup attack) and the proof that ![]() knows the corresponding static private key.
knows the corresponding static private key.
Send (![]() , m):
, m): ![]() sends the message m to party
sends the message m to party![]() . Upon invocation
. Upon invocation ![]() by m, the adversary obtains the outgoing message of
by m, the adversary obtains the outgoing message of![]() .
.
Ephemeral Key Reveal (sid): ![]() obtains the ephemeral private key stored in the session state of session sid.
obtains the ephemeral private key stored in the session state of session sid.
Static Key Reveal (![]() ):
):![]() learns the long-term static private key of an honest party
learns the long-term static private key of an honest party![]() . In this case,
. In this case, ![]() no longer seems honest.
no longer seems honest.
Session Key Reveal (sid): ![]() obtains the session key for the session sid if the session has accepted, otherwise
obtains the session key for the session sid if the session has accepted, otherwise ![]() obtains nothing.
obtains nothing.
Experiment ![]() is given the set P of honest parties and makes whichever queries he wants. The final aim of the adversary is to distinguish a session key from a random string of the same length. Thus
is given the set P of honest parties and makes whichever queries he wants. The final aim of the adversary is to distinguish a session key from a random string of the same length. Thus ![]() selects a complete and fresh session sid, and makes a special query Test(sid). This query can be queried only once, and the session sid is called test session. On this query, a coin b is flipped, if
selects a complete and fresh session sid, and makes a special query Test(sid). This query can be queried only once, and the session sid is called test session. On this query, a coin b is flipped, if ![]()
![]() is given the real session key held by sid, otherwise
is given the real session key held by sid, otherwise ![]() is given a random key drawn from the key space at random.
is given a random key drawn from the key space at random. ![]() wins the experiment if he guesses the correct value of b. Of course,
wins the experiment if he guesses the correct value of b. Of course, ![]() can continue to make the above queries after the Test query; however the test session should remain fresh throughout the whole experiment.
can continue to make the above queries after the Test query; however the test session should remain fresh throughout the whole experiment.
Definition 3.1 (Fresh session). Let sid be a complete session, owned by honest ![]() with honest peer
with honest peer![]() . If the matching session of sid exists, we let
. If the matching session of sid exists, we let ![]() denote the session identifier of its matching session. sid is said to be fresh if none of the following events occurs:
denote the session identifier of its matching session. sid is said to be fresh if none of the following events occurs:
1. ![]() makes a Session Key Reveal (sid) query or a Session Key Reveal (
makes a Session Key Reveal (sid) query or a Session Key Reveal (![]() ) query if
) query if ![]() exists.
exists.
2. If ![]() exists,
exists, ![]() makes either of the following queries:
makes either of the following queries:
(a) Both Static Key Reveal (![]() ) and Ephemeral Key Reveal (sid), or
) and Ephemeral Key Reveal (sid), or
(b) Both Static Key Reveal (![]() ) and Ephemeral Key Reveal (
) and Ephemeral Key Reveal (![]() ).
).
3. If ![]() does not exist,
does not exist, ![]() makes either of the following queries:
makes either of the following queries:
(a) Both Static Key Reveal (![]() ) and Ephemeral Key Reveal (sid), or
) and Ephemeral Key Reveal (sid), or
(b) Static Key Reveal (![]() ).
).
The eCK security notion can be described now.
Definition 3.2 (eCK security). The advantage of the adversary ![]() in the above experiment with respect to the protocol
in the above experiment with respect to the protocol ![]() is defined as ( b is the guessed value of coin by
is defined as ( b is the guessed value of coin by![]() ):
):
![]() (5)
(5)
The protocol ![]() is said to be secure if the following conditions hold:
is said to be secure if the following conditions hold:
1) If two honest parties complete matching sessions, then they will both compute the same session key, except with a negligible probability.
2) The advantage ![]() is negligible.
is negligible.
4. Protocol
Parameters. Let k be the security parameter and G be a cyclic group with generator g and order a k-bit prime p. Let user’s public key is a triple of generators![]() . Parties
. Parties![]() ,
, ![]() static private key is
static private key is![]() , respectvly. Where
, respectvly. Where ![]() public key is
public key is![]() ,
, ![]() public key is
public key is![]() . Let
. Let ![]() to be a cryptographic hash function modeled as a random oracle.
to be a cryptographic hash function modeled as a random oracle.
4.1. Protocol Description
As following description, ![]() will be the session initiator and
will be the session initiator and ![]() the session responder.
the session responder.
1) ![]() chooses randomly an ephemeral private key
chooses randomly an ephemeral private key![]() , computing the ephemeral public key
, computing the ephemeral public key ![]() and sends
and sends ![]() to
to![]() .
.
2) Upon receiving![]() ,
, ![]() verifies that
verifies that![]() . if so,
. if so, ![]() chooses randomly an ephemeral private key
chooses randomly an ephemeral private key![]() , computing the ephemeral public key
, computing the ephemeral public key ![]() and sends
and sends ![]() to
to![]() . Then
. Then ![]() computing the shared secret
computing the shared secret![]() , the session
, the session ![]() and competes the session.
and competes the session.
3) Upon receiving![]() ,
, ![]() checks if he owns a session with
checks if he owns a session with ![]()
![]() . if so,
. if so, ![]() verifies that
verifies that![]() . if so,
. if so, ![]() computing the shared secret
computing the shared secret![]() , the session
, the session ![]() and competes the session. Figure 1 shows the protocol description.
and competes the session. Figure 1 shows the protocol description.
Both parties compute the shared secret
![]() (6)
(6)
![]() (7)
(7)
![]()
Figure 1. Tightly-Secure Authenticated Key Exchange without NAXOS’ approach based on Decision Linear Problem.
4.2. Protocol Security
Theorem 4.1. If the DLIN assumption holds in G and H is a random oracle, then the Protocol ![]() is eCK-secure.
is eCK-secure.
Let ![]() be a polynomial bounded adversary against protocol
be a polynomial bounded adversary against protocol![]() ,
, ![]() is the target session chosen by adversary
is the target session chosen by adversary![]() ,
, ![]() is the owner of the session
is the owner of the session ![]() and
and ![]()
is the peer. Let ![]() be
be ![]() where
where ![]() is public keys for
is public keys for ![]() respectively, (
respectively, (![]() ). Assume also that
). Assume also that ![]() is adversary advantage which we want to evaluate in
is adversary advantage which we want to evaluate in
this proof. Let ![]() is the number of parties chosen bt adversary and let
is the number of parties chosen bt adversary and let ![]() is the number of sessions chosen by the adversary in challenge game. We will have this two events:
is the number of sessions chosen by the adversary in challenge game. We will have this two events:
-case 1: Existence of a matching session ![]() for the target session
for the target session![]() .
.
-case 2: No existence of a matching session for the target session![]() .
.
Case 1. To analyze this event, Adversary ![]() will play next games,
will play next games, ![]() and
and ![]() as follows:
as follows:
-![]() : This is eCK original game where adversary try to distinguish the real session key from random string. For game state, see Appendix A.1.
: This is eCK original game where adversary try to distinguish the real session key from random string. For game state, see Appendix A.1.
Claim. let ![]() be the event that
be the event that ![]() in
in![]() . we claim that
. we claim that
![]() (8)
(8)
Proof. It’s easy to derive the proof from definition 3.2
-![]() : This is reduced game from
: This is reduced game from![]() , In this game the adversary will choose only two parties , and only two sessions, the target session and its matching session (
, In this game the adversary will choose only two parties , and only two sessions, the target session and its matching session (![]() ) with identifiers (
) with identifiers (![]() ) and (
) and (![]() ) respectively. For game state, see Appendix A.2.
) respectively. For game state, see Appendix A.2.
Claim. let ![]() be the event that
be the event that ![]() success in guessing
success in guessing ![]() in
in![]() . we claim that
. we claim that
![]() (9)
(9)
Proof. In this game, it obvious that this game is similar to game ![]() except it required adversary to guess target session and its matching session correctly to win this game. To select correct parties
except it required adversary to guess target session and its matching session correctly to win this game. To select correct parties ![]() aad
aad ![]() , adversary should choose between
, adversary should choose between ![]() parties the couple (
parties the couple (![]() ), Let
), Let ![]() denotes that event, thus:
denotes that event, thus:
![]()
In another hand, the adversary should success in guessing target session and its matching session. Let ![]() denote the probability that adversary successfully guess the target session and its matching session thus:
denote the probability that adversary successfully guess the target session and its matching session thus:
![]()
![]()
thus
![]()
From these two probabilities, we can derive the whole probability that adversary success in guessing parties ![]() and
and ![]() with target session and its matching session with the form:
with target session and its matching session with the form:
![]()
-![]() : We transform
: We transform ![]() into
into![]() , computing values
, computing values
![]() to random value
to random value ![]()
where![]() . For game state, see Appendix A.3.
. For game state, see Appendix A.3.
Claim. let ![]() be the event that
be the event that ![]() success in solving DLIN problem in
success in solving DLIN problem in![]() . we claim that
. we claim that
![]() (10)
(10)
Proof. We transform game ![]() into
into ![]() computing values
computing values
![]() to random value
to random value ![]()
where![]() . If adversary success in distinguishing between
. If adversary success in distinguishing between ![]() and
and ![]() with non-negligible probability, then he can solve the DLIN problem, thus we construct adversary that solves DLIN problem. In this game, will choose same parameters in
with non-negligible probability, then he can solve the DLIN problem, thus we construct adversary that solves DLIN problem. In this game, will choose same parameters in ![]() except values (
except values (![]() ) which will be chosen randomly. There for we obtain:
) which will be chosen randomly. There for we obtain:
![]()
-![]() : We transform
: We transform ![]() into
into![]() , computing h by choosing it at random, rather than as a hash function. For game state, see Appendix A.4.
, computing h by choosing it at random, rather than as a hash function. For game state, see Appendix A.4.
Claim. let ![]() be the event that
be the event that ![]() success in distinguishing value H from random string in
success in distinguishing value H from random string in![]() . we claim that
. we claim that
![]() (11)
(11)
which ![]() is ES-advantage of some efficient algorithm( which is negligible assuming
is ES-advantage of some efficient algorithm( which is negligible assuming ![]() is entropy smoothing).
is entropy smoothing).
Proof. We will prove here using the same idea in the previous game. In this game we transformed from ![]() by changing the hash value with a random value. The difference between
by changing the hash value with a random value. The difference between ![]() and
and ![]() can be parlayed into a corresponding ES-advantage.
can be parlayed into a corresponding ES-advantage.
Moreover, as h act as a one-time pad in game![]() , it's evident that
, it's evident that
![]() (12)
(12)
Combining (8), (9), (10), (11) and (12), we obtain
![]() (13)
(13)
Case 2. To analyze this event, Adversary ![]() will play next games,
will play next games, ![]() and
and ![]() as follows:
as follows:
-![]() : This is an eCK original game where adversary
: This is an eCK original game where adversary ![]() try to distinguish the real session key from a random string. For the game state, see Appendix A.5.
try to distinguish the real session key from a random string. For the game state, see Appendix A.5.
Claim. let ![]() be the event that
be the event that ![]() in
in![]() . we claim that
. we claim that
![]() (14)
(14)
Proof. That proof can be derived from![]() .
.
-![]() : This is reduced game from
: This is reduced game from![]() , In this game the adversary will choose only two parties
, In this game the adversary will choose only two parties ![]() and only target session (
and only target session (![]() ) with identifier (
) with identifier (![]() ). For game state, see Appendix A.6.
). For game state, see Appendix A.6.
Claim. let ![]() be the event that success in guessing
be the event that success in guessing ![]() in
in![]() . we claim that
. we claim that
![]() (15)
(15)
Proof. In this game, it is obvious that this game is similar to game ![]() except it's required the adversary to guess target session correctly to win this game. To select correct parties
except it's required the adversary to guess target session correctly to win this game. To select correct parties ![]() nad
nad![]() , adversary should choose between
, adversary should choose between ![]() parties the couple(
parties the couple(![]() ), Let
), Let ![]() denotes that event, thus:
denotes that event, thus:
![]()
In another hand, the adversary should success in guessing target session and its matching session. Let Pr[sidA;B], denote the probability that adversary successfully guess the target session from ![]() sessions, thus:
sessions, thus:
![]()
From these two probabilities, we can derive the whole probability that adversary success in guessing parties and with target session and its matching session with the form:
![]()
-![]() : We transform
: We transform ![]() into
into![]() , computing values
, computing values ![]() randomly as
randomly as ![]() which lead to computing value
which lead to computing value ![]() from random values which make it random value. For the game state, see Appendix A.7.
from random values which make it random value. For the game state, see Appendix A.7.
Claim. let ![]() be the event that
be the event that ![]() success in solving DLIN problem in
success in solving DLIN problem in![]() . we claim that
. we claim that
![]() (16)
(16)
Proof. We transform game ![]() into
into ![]() computing values
computing values ![]() randomly as
randomly as ![]() which lead to compute value
which lead to compute value ![]() from random values which make it random value. If adversary success in distinguishing between
from random values which make it random value. If adversary success in distinguishing between ![]() and
and ![]() with non-negligible probability, then he can solve the DLIN problem, thus we construct adversary
with non-negligible probability, then he can solve the DLIN problem, thus we construct adversary ![]() that solve DLIN problem. In this game,
that solve DLIN problem. In this game, ![]() will choose same parameters in
will choose same parameters in ![]() except values
except values ![]() which will be chosen randomly. Then he will query oracle machine for tuple
which will be chosen randomly. Then he will query oracle machine for tuple![]() , if a tuple exists oracle will return corresponding
, if a tuple exists oracle will return corresponding ![]() to the adversary, else oracle will return random value to an adversary. So we can make
to the adversary, else oracle will return random value to an adversary. So we can make ![]() queries oracle without repeating the same query to oracle. In case repeating the same query we will get halt with probability of:
queries oracle without repeating the same query to oracle. In case repeating the same query we will get halt with probability of:
![]()
There for, we obtain:
![]()
-![]() : We transform
: We transform ![]() into
into![]() , based on transform hash function
, based on transform hash function ![]() with random oracle function
with random oracle function![]() . For game state, see Appendix A.8.
. For game state, see Appendix A.8.
Claim. let ![]() be the event that
be the event that ![]() success in distinguishing value
success in distinguishing value ![]() from random oracle
from random oracle ![]() in
in![]() . we claim that
. we claim that
![]() (17)
(17)
which ![]() is ES-advantage of some efficient algorithm( which is negligible assuming
is ES-advantage of some efficient algorithm( which is negligible assuming ![]() is entropy smoothing).
is entropy smoothing).
Proof. We will prove here using the same idea in the previous game. In this game we transformed from ![]() by changing the hash value with a random value generated by oracle. Without losing of generality, The adversary will make
by changing the hash value with a random value generated by oracle. Without losing of generality, The adversary will make ![]() queries to oracle without a repeat of the same query. Same idea in previous game we can get the probability of halt as:
queries to oracle without a repeat of the same query. Same idea in previous game we can get the probability of halt as:
![]()
The difference between ![]() and
and ![]() can be parlayed into a corresponding ES-advantage.
can be parlayed into a corresponding ES-advantage.
Moreover, as h act as a one-time pad in game![]() , it’s evident that
, it’s evident that
![]() (18)
(18)
Combining (14), (15), (16), (17) and (18), we obtain
![]() (19)
(19)
From the sequence of preceding claims, we can conclude that since the ![]() , and since
, and since ![]() is negligible in k-from DLIN assump- tion-thus our protocol is secure based on decision linear assumption in random oracle model.
is negligible in k-from DLIN assump- tion-thus our protocol is secure based on decision linear assumption in random oracle model.
5. Efficiency
In this section, we compare our protocols with other related AKE protocols in terms of based assumption, computational efficiency and security model. In Table 1 number of exponentiation in G (E), a number of static public keys (SPK) and the number of ephemeral public key (EPK). Table 5 presents the naive group exponentiations count; Okamoto’s protocol is secure in the standard model, but the proof relies on an existence of pPRF family. In the security proof of HMQV and CMQV, the reduction argument is less tight since the Forking Lemma [14] is essential for the arguments. Our protocol in Table 1, has tighter security reductions and does not use the Forking Lemma and just uses one static public key in computation.
It clear that our protocol has same security model with NETS, CMQV, and KFU-P1, but it differs from them in base assumption and computation.
We showed that it is possible to construct eCK-secure AKE protocols without using NAXOS’ approach, so our protocol is secure even when the discrete logarithm of the ephemeral public key is revealed and decrease the risk of leaking the static private key which makes our protocol more practical.
Moreover, One of the advantages of our protocols is the use of single random oracle as opposed to two for HMQV and CMQV. The random oracle is merely needed for the session key derivation, which is typical way to attain indistinguishability in random oracle model.
Also, our protocol uses decision linear assumption with a tight security proof.
6. Conclusion
In this paper, we present AKE protocol secure in the eCK model under Decision Linear assumption(DLIN) without using NAXOS trick with a fastened reduction, which reduces the risk of leaking the static private key, that because of the derivation of the ephemeral public key is independent of the static private key. This is in contrast to protocols that use the NAXOS’ approach, and minimize the use of the random oracle, by applying it only to the session key derivation. We gave tightly security proof for our protocol based on games. In this paper, how to preserve the security of to this protocol without using random oracle remains as an open problem.
Appendix
A.1 ![]()
![]()
A.2 ![]()
![]()
A.3 ![]()
![]()
A.4 ![]()
![]()
A.5 ![]()
![]()
A.6 ![]()
![]()
A.7 ![]()
![]()
A.8 ![]()
![]()
![]()
Submit or recommend next manuscript to OALib Journal and we will provide best service for you:
Publication frequency: Monthly
9 subject areas of science, technology and medicine
Fair and rigorous peer-review system
Fast publication process
Article promotion in various social networking sites (LinkedIn, Facebook, Twitter, etc.)
Maximum dissemination of your research work
Submit Your Paper Online: Click Here to Submit
Or Contact service@oalib.com