A Novel Transceiver Architecture Based on Wavelet Packet Modulation for UWB-IR WSN Applications ()
1. Introduction
The Wide-Band or Ultra-Wide Band applications such as the multimedia services based generally on wireless sensors systems [1] - [5] . Several techniques are proposed in literature especially for digital communication based on two systems: narrow-band and multi-carrier [6] - [8] . This last are developing different technique in transmitter and receiver like Modulation, MAC protocol, Equalization, Filtering, Fading, Multi-path, and Non-Line-Of-Sight (NLOS) [7] [9] . Other distribution of this system named IR (Impulse Radio), present all data in impulse form.
In this complex and constrained context, one of the challenges relies on the use of the impulse radio and ultra-wideband communications. Today, the ultra-wideband technology gain in popularity in short-range communications systems, some multimedia transmission systems require a very wide bandwidth, this bandwidth being assured by the impulse techniques [1] - [3] [10] [11] .
The impulses present common characteristics: they are generated in baseband, possess a very short duration of few nanoseconds authorizing a bandwidth of at least 500 MHz, and respect the masks of transmission defined in US by the FCC (Federal communications Commission) and in Europe by the RSC (Radio Spectrum Committee), by two masks indoor and outdoor [3] [4] . These impulse radio (IR) systems are characterized by various techniques dedicated to the wireless broadband communications: transmission, multiplexing, modulation and detection. The needs regarding the number of users, the number of paths, the frequency bands, but also the very low power emission, require the implementation of very strong methods. In the impulse-Radio UWB communication systems, the pulse constitutes the support of the information and its transmission requires an operation of simple modulation controlled by binary states, like OOK (on-off keying), PPM (Pulse Position Modulation), BPSK (Binary Phase Shift Keying) with only one shape pulse and after a complexity in the MAC layer [7] [11] - [13] . The necessity of detecting the pulses at the reception stage allows envisaging other models of modulations that consider the shape of the impulse. This Pulse Shape Modulation (PSM) induces difficulties both for the transmitter (generation of a pulse depending on a state) and for the receiver (pulse detection and shape recognition). With this technique the complexity are focalized in physical layer with possibility of merger with MAC layer.
In the literature, there are a large number of forms of impulses using in the transmission such as the Gaussian and its derivate, the impulses of Nyquist, the orthogonal polynomials and also the wavelet [11] [12] . The model usually used at the beginning of systems UWB was the Gaussian monocycle. After, this model was abandoned and replaced by Gaussian wavelet obtained by multiplication of a Gaussian by a sinusoidal signal. Another family of systems based on the orthogonal polynomials (Hermite, Gegenbauer, and others). More recently, the use of the wavelet transform is proposed to generate the orthogonal impulses.
In [14] , the authors proposed on new concept for MICT (medical information communication technology) based on multiuser UWB-BAN Communication using a complex modified Hermite pulse. The objective of authors is to propose a pulse communication for multiuser Body Area Network (BAN) applications and testing interference between users using Orthogonal Matched Filters based on Hermite Pulse. In [15] , the authors propose a BER analysis of UWB communication based on Pulse Position Modulation (PPM) using different forms of impulse: Gaussian modified Hermite and composite Hermite pulse. The authors are testing the proposed architecture in several channel models to improve the performance of proposed architecture.
With the same objectives, in this paper we will propose a new concept of impulse transceiver design based on Inverse Discrete Wavelet Packet Transform in emitters and Discrete Wavelet Packet Transform in receiver for digital communication. We propose also two modes of communication: i) multi-channel architecture with two modes of bandwidth allocation: one channel per user in the peer-to-peer mode, several channels per user in the multiusers mode; ii) a single receiver capable on one hand of detecting the data sent by all the broadcasting stations following both proposed modes, and on the other hand to identify the transmitter.
The rest of this paper is organized as follows: section 2 present a state of art. All description of our proposed will be presented in section 3. The validation of pulse forms based on IDWPT will be presented in section 4. The concept of modulation using in this paper are presented in section
2. Wavelet Discrete Transform
Spread spectrum techniques for wideband communications often rely on the Discrete Fourier Transform (DFT) that presents some limitations concerning the analysis of the non-stationary signals, because this transform doesn’t consider the information in a temporal structure of the signal, what induces a difficulty in localizing the discontinuity of the signal [16] . The solution brought at first was the Windowed Fourier Transform (WFT) which compares the signal with a sinusoid of infinite duration within a time-limited window. The Discrete Wavelet Transform (DWT) presents a better solution by bringing a good compromise between time and frequency of analysis. The peculiarity of this transform is that it mixes both notions of time and scale contrary to the Fourier transform which assures the passage from a notion to another. The performances of the DWT algorithms and the multi-resolution analysis authorize a large diversity of applications relying on the wavelets theory. These algorithms are based on several methods among which the filter banks constitute the most often implemented solution. The multi-resolution analysis allows the decomposition of the signal into coefficients of approximation and details, from a scaling function and a wavelet function, respectively [8] [17] . This implementation is based on a set of cascaded low-pass and high-pass digital filters (Figure 1).
In the wavelet transform (WT) theory, the wavelet basis functions are obtained from a single prototype function called “wavelet” by translation and dilation or contraction:
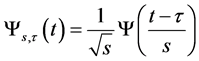 (1)
(1)
where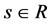 . For large 𝑠, the basis function becomes a stretched version of the prototype wavelet, that is a low frequency function, while for small 𝑠, the basis function becomes a contracted wavelet, that is a high frequency function.
. For large 𝑠, the basis function becomes a stretched version of the prototype wavelet, that is a low frequency function, while for small 𝑠, the basis function becomes a contracted wavelet, that is a high frequency function.
The Continue Wavelet Transform (CWT) of x(t) is defined as:
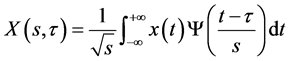 (2)
(2)
where * denotes complex conjugation.
![]()
Figure 1. Decomposition and reconstruction using filter bank based on high pass and low pass filters.
The CWT is too redundancy and to make it practical, we need a finite number of wavelets in the wavelet transform. Therefore, the discrete wavelets transform (DWT) are discretely scalable and translatable. This was achieved by modifying the wavelet representation to create Daubechies (1992) [16] :
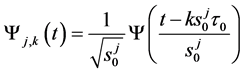 (3)
(3)
We usually choose  so that the sampling of the frequency axis corresponds to dyadic sampling. In addition,
so that the sampling of the frequency axis corresponds to dyadic sampling. In addition,  we gave a dyadic sampling in time.
we gave a dyadic sampling in time.
Discretizing the translation and dilation contraction parameters of the wavelet in (1), the dyadic discrete WT of x(t) is:
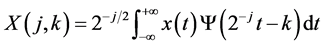 (4)
(4)
where .
.
It should be mentioned that WT can be implemented by non-uniform filter banks. Where the input signal separates into low frequency component signal and high frequency component signal. The first is called smooth coefficient, the second part is called wavelet coefficients. The smooth coefficient is separated into two parts repeatedly). In the classical way, we indicate the tow part via low-pass digital filter H and a high pass-filter G. By using the scaling function and there corresponding mother wavelets, we obtain both of the digital filter H and G. We suppose H and G like a FIR filters non-recursive with L length, the transfer functions of H and G can be represented as follows:
 (5)
(5)
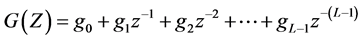 (6)
(6)
Mallat’s tree algorithm or pyramid algorithm [2] can be used to find the multiresolution decomposition of DWT, the two scale relations (5) and (6) leads to scaling functions and wavelet functions similar to that in scalar wavelets. But the equations are two scale matrix equations and can be given as:
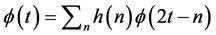 (7)
(7)
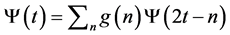 (8)
(8)
where 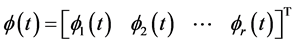 and
and 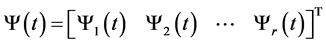 forms the set of scaling functions and corresponding wavelets. The suffix r denotes the number of wavelets and is dubbed as multiplicity. The decomposition DWPT at each resolution level can be presented as tree shape.
forms the set of scaling functions and corresponding wavelets. The suffix r denotes the number of wavelets and is dubbed as multiplicity. The decomposition DWPT at each resolution level can be presented as tree shape.
3. Our Proposed Architecture
In this section, we will present all information about our proposed architecture. It should be noted that all emitters are based on the IDPWT implemented as a synthesis filter banks, and the receiver is based on the DWPT implemented as an analysis filter banks (Figure 2). This architecture can be configured to suit the targeted application: the wavelet and the depth of the transform can be chosen to adapt the shape of the generated impulse but also, according to the mode of use, to define the maximum through put and the number of simultaneously exploitable sensors or users. Indeed, two modes of coding are possible: The many-to-one mode that maximizes the number of transmitting nodes but reduces the throughput Figure 2(b), and the peer-to-peer mode that maximizes the throughput but reduces the number of nodes that can transmit at the same time Figure 2(a).
3.1. Peer-to-Peer Mode
For the peer-to-peer communication, and with the same way as in [18] - [21] . The main objective of this mode is using of all inputs of IDWPT bloc just only for one users, every input corresponding to a bit of data; for example at the scale 2 of wavelet we shall have 16 inputs. All inputs will be activate by a binary word of 16 bits, as shown in
![]()
Figure 2. (a) Mono user transceiver (b) multi user transceiver.
Figure 3. Synthesized by the cascade of synthesis filters, the wavelet corresponding to this word of 16 bits will be generated and using like a series of pulse. With this strategy, one user (sensor) can used this architecture, and data will be limited by wavelet scale. Figure 3 shows how data can be used in peer-to-peer mode based on scale 4 of wavelet.
3.2. Multiuser Mode
In this mode, the use of the IDWPT/DWPT is different from what was presented in others works [18] [19] : The number of users is specified, and for every users an IDWPT block is implemented. The main objective of our strategy is to assure on one hand the activation of only one input per user, and on the other hand, this input corresponds to a given level of details and approximation that will be used as identification label, and the unused inputs are all forced to zero. Consequently, the activation of one input per user, the throughput per user can reduced, but the overall system’s throughput is the same compared with peer-to-peer mode, as shown in Figure 4.
The receiver in both of the case peer-to-peer and multiuser is based on DWPT. This last is presented like a cascade filter is dedicate to the reception and split of the data flow into separate channels, and a decision block ensures the detection and the correction of data and identification of the emitter. The detection operation consists in studying the amplitude of the received signals and thresholding for decision-making and recognition. Figure 5 shows two modes of communication with the same receiver.
3.3. Mathematical Description
In this section, we will present global mathematical description for data sending and receiving presented in Figure 6. With this presentation, we can describe the functioning
![]()
Figure 4. One emitter bloc from multi user mode.
of IDWPT/DWPT architecture.
The wavelet in emitter is presented like this:
![]() (9)
(9)
![]() is presented like this:
is presented like this:
![]() (10)
(10)
The wavelet coefficient is obtained by dot product of the input with the mother wavelet:
![]() (11)
(11)
when replaces the factor by the scalar product we obtain:
![]() (12)
(12)
![]() (13)
(13)
After passing through the high pass filters and low pass we will have:
![]() (14)
(14)
The scaling function is calculated as follows:
![]() (15)
(15)
![]() (16)
(16)
As for the wavelet function, its is calculated as follows:
![]() (17)
(17)
![]() (18)
(18)
Substituting in the main equation we get:
![]()
Figure 5. IDWPT/DWPT for both peer-to-peer (b) and multiuser (a) modes.
![]()
Figure 6. IDWPT/DWPT architecture with 1 scale.
![]() (19)
(19)
This shows that:
![]() (20)
(20)
The approximation is defined as:
![]() (21)
(21)
with: ![]()
So:
![]() (22)
(22)
For: ![]()
So :
![]() (23)
(23)
The detail is defined as:
![]() (24)
(24)
with:![]() :
:
![]() (25)
(25)
For: ![]()
So:
![]() (26)
(26)
This implies that:
![]() (27)
(27)
Regarding the transmission chain we can conclude:
![]() (28)
(28)
4. Impulse Forms and Characteristics
In sections II and III we are presented the necessity of IDWPT to generate different form of pulses based on binary data like input. In this section, we will describe the forms of impulse generate using only IDWPT bloc. The study of the form of impulse is very important especially for Impulse Radio for UWB systems. Indeed, all characteristics presented in section III and especially the Mallat algorithm proposed optimal techniques help to generate different pulses that the duration depends on the scales and the characteristics of filters for such wavelet. Every IR-UWB system has to deal with the impulse synthesis. This step is even more crucial in the case of impulse modulation, where different pulses shapes have to be generated.
4.1. Pulse Forms Based IDWPT
In this section, we will described technics using to generate different form pulse for our proposed. Like presented in section III, the IDWPT bloc presented like a generator of pulse in both of peer-to-peer and multiuser modes. In peer-to-peer mode, we active all input of one emitter IDWPT bloc. With this mode, we generate a series of different pulse. In our proposed, we active only one input per user to generate pulse form especially for this user. In the case of scale 4 of wavelet, we can implement 16 users, and each user generate here pulse shape. Figure 7 shows different pulse shape per user. The goal of each user is modulate the input data using the Mallat-tree algorithm for reconstruction using IDWPT, the main operating is like this: when we activated only one input from 16 inputs or coefficient for scales 4 cases, we can modulate the binary data in impulse signal this technique can: i) use indirectly one type of modulation presented in next section ii) generate different form of impulse from different input iii) using orthogonal impulse.
4.2. PSM Based OOK Modulation
The IR-UWB systems use very often a type of impulse known as monocycle. The use of impulses instead of sinusoids to carry the information raises many questions relative to the generation of the impulses shapes, their modulation and the coding of the impulses trains [22] . After the generation of the impulse, its transmission requires an operation of modulation. Several methods were proposed but few present an important self-robustness regarding to the narrowband techniques and short-range communication’s systems. The techniques of impulse modulation mostly rely on the following methods: PWM, PAM and PSM. The PWM (Pulse Width Modulation) consists in differentiating states by using the impulse’s width. PAM (Pulse Amplitude Modulation) consists in modulating the amplitude of the impulse according to the information; It should be noted that OOK and BPSK techniques correspond to an amplitude modulation with coefficients of [0, 1] and [−1, 1] respectively. The PSM (Pulse Shape Modulation) consists in generating several forms of impulses according to the information. This technique is very robustness because allows to generate a lot of shape of pulse, it present same difficulties but present a simplicity in MAC layer. In our architecture we are using the PSM modulation with OOK for every sensor of architecture, the principle is like that : we are generate a lot of shape pulse and identify every sensor with one pulse shape, after the modulation using for every sensor is just only OOK for multiuser mode see Figure 8, and with different PSM for mono-user mode.
4.3. FCC Validation
For our architecture, we are using IDWPT to generate many forms of impulses for objective to generate a series of impulses adapted in which data sending in UWB-IR context. In this architecture, the activated of all input or some input can generate series impulses but not special techniques of modulation. The activation of one input can generate series of impulse with indirectly OOK or PSM modulation (which will be
![]()
Figure 7. Pulse form per user in multiuser mode.
presented in the next section), but for which users we can generate one form of impulse. For example, when we use scale 4, the sixteen users (all users) can send in the same time but also the sixteen form of impulse can generate. We suggest using the IDPWT as an impulse generator for the emitter: the corresponding synthesis filter bank will generate a wavelet whose shape depends on the data at the 2i inputs of the filter bank, i being the resolution level of the transform. Depending on the functioning mode, the different wavelets shapes will thus be used either to spread the data all over the bandwidth, or to distinguish between different users. Figure 9, Figure 10 and Figure 11 show the validity of pulses in the FCC mask.
![]()
Figure 9. Daubechies 2 wavelet input number 15 activated.
![]()
Figure 10. Coifelet wavelet input number 13 activated.
![]()
Figure 11. Symlet 2 wavelet input number 12 activated.
5. Simulations and Results
After validated of pulses in the masque of FCC (3.1 - 10.6 GHz) for respect the basic rules of UWB-IR in the previous part, in this part we will present global description of our transmitter and how with the proposed technique we can generate sending and receiving. In section II, we are present same basic techniques about DWPT and we are explaining clearly the difference between decomposition and reconstruction, in our architecture each bloc of user collect data and construct a synthetic data collected as impulse signal.
In this part, we will present how all emitters can send in the same time to one receiver, and how this last can decompose and detect the data receiver. This architecture is limited only in scale 4 for 16 users to respect role of FCC dedicated to UWB applications. The band is (3.1 - 10.6 GHz) globally 7.5 GHz for all users about this systems, each user can occupy only 500 MHz. For this reason, our proposed is only valid to application with 16 sensors max. After construction of data by all sensors, we are fusing the all signal to one receiver (signal presented in Figure 12), all information are presented in Table 1. The receiver has a double mission are detected both of data and sensor. When users send to one receiver, the data are centralized to the receiver but before centralized, the system proceeded to summons all signal and sending just one signal. The signal received are decomposed in the received using DWPT, and we are going to reconstruct 16 signal, each output present a signal and when activated one input. We
![]()
Table 1. Characterics of the architecture.
are systematically choosing the output related on input, it has become easy for the receiver to detect of both data and sensor (Figure 13 shows frequency band for 8 users).
To evaluate the performance of our proposed architecture, we are proceed on Bit Error Rate study (BER) over the Signal to Noise Ratio (SNR). We are using AWGN channel as a performance measure for the proposed technique, we use the BER/SNR with an additive white Gaussian noise with 8, 16 users.
In Figure 14, Figure 15, Figure 16 and Figure 17 we can show a sensible BER with different values of additive white Gaussian noise (AWGN), where we are used as wavelet Daubechies (Db4) and Symlet for two reason: most of recent work was used Daubechies wavelet and then able to compare later, second reason the compromise between Daubechies wavelet and there filter order (2N).
6. Conclusion and Perspectives
A novel form of impulse communication architecture was proposed in this work, based on IDWPT in all emitters and DWPT in receiver for wireless and multi-users digital communication. This structure allowed our proposed multichannel communication model for reconfigurable transceiver input by following the block that this entity IDWPT issue of each user who belongs of architecture. This architecture is adapted to intra-cluster transmissions from several nodes to one sink, and the use of the DWT allows sparing the signal correlation stage, hence permitting a low power consumption. We have focused on the transmitter and receiver architectures, and the simulations that have been performed show the phenomena relative to pulse generation, number of
![]()
Figure 14. BER/SNR as a function of SNR for 16 users using DB4.
![]()
Figure 15. BER/SNR as a function of SNR for 8 users using DB4.
![]()
Figure 16. BER/SNR as a function of SNR for 16 users using Sym4.
![]()
Figure 17. BER/SNR as a function of SNR for 8 users using Sym4.
sensors, and bandwidth used for each user.