
1. Introduction
As known [1] a quantum physical system can be represented by a couple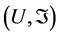 , where
, where 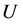 is some
is some ![]() -algebra which are hermit’s elements that are called observables and some set
-algebra which are hermit’s elements that are called observables and some set ![]() of positive functional with norm one, called the quantum states of this physical system [2] .
of positive functional with norm one, called the quantum states of this physical system [2] .
We say what the functional ![]() majorizes functional
majorizes functional ![]() if
if ![]() is a positive functional [2] .
is a positive functional [2] .
The state ![]() quantum physical system is called the pure state if it majorizes only functional type
quantum physical system is called the pure state if it majorizes only functional type ![]() [2] . Denote the set of all pure states on
[2] . Denote the set of all pure states on ![]() -algebra
-algebra ![]() by
by![]() .
.
In the set of all linear continuous functional on ![]() -algebra
-algebra ![]() we have topological structure, called as
we have topological structure, called as ![]() weakly topological structure [2] and defined by pre-basis:
weakly topological structure [2] and defined by pre-basis:
![]() ,
,
where![]() ; according to this in the set
; according to this in the set ![]() we have the topological structure induced from this topological structure.
we have the topological structure induced from this topological structure.
It is very known if ![]() commutative
commutative ![]() -algebra, then every positive linear functional defines complex valued measure on the
-algebra, then every positive linear functional defines complex valued measure on the ![]() which is separable and locally compact space of pure states under the * weekly topological structure. This measure is
which is separable and locally compact space of pure states under the * weekly topological structure. This measure is
defined by corresponding![]() ,
, ![]() , for all
, for all ![]() continuous
continuous
function. In non-commutative case we cannot define the measure on ![]() in this way. In the work [3] for each linear functional, with norm one, we define the probability measure
in this way. In the work [3] for each linear functional, with norm one, we define the probability measure ![]() for commutative and non-commutative cases in other ways. It gives us the opportunity to present a quantum physical system as a statistical structure [4] . Representation of quantum physical system in this form, in our opinion, is more comfortable for the solution of problem of quantum system, for example for testing hypotheses [4] . In this paper, using this representation, we have tried to consider the dynamic of quantum physical system as a random process.
for commutative and non-commutative cases in other ways. It gives us the opportunity to present a quantum physical system as a statistical structure [4] . Representation of quantum physical system in this form, in our opinion, is more comfortable for the solution of problem of quantum system, for example for testing hypotheses [4] . In this paper, using this representation, we have tried to consider the dynamic of quantum physical system as a random process.
2. Quantum Physical System as a Statistical Structure
Denote by ![]() the set of Hermit’s elements of
the set of Hermit’s elements of ![]()
![]() -algebra.
-algebra.
Easy to show that every linear functional on the ![]()
![]() -algebra uniquely will be defined by its values on Banach subspace of Hermit’s elements,as it’s known [2] that every element
-algebra uniquely will be defined by its values on Banach subspace of Hermit’s elements,as it’s known [2] that every element ![]() of
of ![]() -algebra
-algebra ![]() uniquely represented as
uniquely represented as![]() , where
, where ![]() and
and ![]() are Hermit’s.
are Hermit’s.
Every a Hermit’s element ![]() in the
in the ![]() -algebra
-algebra ![]() any can be represented by integral
any can be represented by integral
![]() ,
,
where ![]()
![]() projectors and represents the partition of unityof Hermit’s element
projectors and represents the partition of unityof Hermit’s element ![]() [5] .
[5] .
Correspond to projector ![]() the family
the family ![]() of elements of the
of elements of the ![]() - algebra
- algebra ![]() which has the condition:
which has the condition:![]() , if
, if![]() ,
, ![]() , if
, if ![]() and
and![]() , if
, if![]() , where
, where ![]() is the unit element in the algebra
is the unit element in the algebra![]() . It is clear that.
. It is clear that.
![]() .
.
If![]() , then
, then![]() , where
, where ![]() and
and ![]() are Hermit’s elements. The representation such
are Hermit’s elements. The representation such ![]() will be
will be
![]() ,
,
Obviously, if ![]() some linear continuous functional on
some linear continuous functional on ![]() -algebra
-algebra![]() , then from the last equality we will have
, then from the last equality we will have
![]() ,
,
where ![]() and
and ![]() are Hermit’s elements.
are Hermit’s elements.
Let, ![]() be the set of all one dimensional projectors on
be the set of all one dimensional projectors on ![]() -algebra
-algebra ![]() and
and ![]() pure state, then the last equality follows that this state has the non zero meaning only on some projector
pure state, then the last equality follows that this state has the non zero meaning only on some projector ![]() and the meaning 0 on the other one dimensional projectors. Otherwise, we can always construct such functional which will not have the type
and the meaning 0 on the other one dimensional projectors. Otherwise, we can always construct such functional which will not have the type ![]() and well majorized by the pure state
and well majorized by the pure state![]() . So how, if functional
. So how, if functional ![]() is a pure state, then
is a pure state, then ![]() for all Hermit’s elements
for all Hermit’s elements![]() .
.
Let, ![]() and
and ![]() such functional, which has the non zero meaning
such functional, which has the non zero meaning ![]() only on some projector
only on some projector ![]() and the meaning 0 on the other one dimensional projectors. It is clear, if we take
and the meaning 0 on the other one dimensional projectors. It is clear, if we take ![]() sufficiently small, thenwe can achieve, that for every
sufficiently small, thenwe can achieve, that for every ![]() will have place inequality
will have place inequality
![]() .
.
It means, that the pure state ![]() majorize the functional
majorize the functional ![]() which does not have the type
which does not have the type![]() , but this is impossible. It follows that the pure states are sach functional which satisfy the condition
, but this is impossible. It follows that the pure states are sach functional which satisfy the condition![]() .
.
An integral representation of Hermit’s elements follows that for the pure states ![]() has a place of equality
has a place of equality![]() , where
, where ![]() is some element of spectrum of Hermit element
is some element of spectrum of Hermit element![]() . It gives opportunity to identify every pre state with the set of number
. It gives opportunity to identify every pre state with the set of number![]() , where
, where![]() .
.
Consider the Tikhonov’s product![]() , where
, where ![]() spectrum of element
spectrum of element![]() .
.
It is clear, ![]() , because
, because ![]() the set of such elements in product
the set of such elements in product ![]() which represents linear continue maps with respect to the topological structure in
which represents linear continue maps with respect to the topological structure in ![]() which is defined by the norm:
which is defined by the norm:
![]() .
.
Consequently in the set ![]() we have
we have![]() , induced from Tikhonov’s product
, induced from Tikhonov’s product ![]() topological structure. This topological structure coincide with theinduced topological structure from
topological structure. This topological structure coincide with theinduced topological structure from ![]() weakly topological structure on set of functionals on
weakly topological structure on set of functionals on ![]() algebra
algebra![]() .
.
We can also identify the set ![]() with the set of one dimensional projectors
with the set of one dimensional projectors![]() . We call
. We call ![]() as physical space of quantum system.
as physical space of quantum system.
In the work [3] we have proved:
Theorem 1. Every state ![]() in space
in space ![]() with
with ![]() weakly topological structure, defined on the Borel
weakly topological structure, defined on the Borel ![]() -algebra of a probability measure
-algebra of a probability measure![]() .
.
This measure constructed as: for the subset ![]() of
of![]() , measure
, measure ![]() is norm of positive functional
is norm of positive functional![]() ,
, ![]() , if this exists, which values on the elements of this subset are coincide to corresponding to values of the state
, if this exists, which values on the elements of this subset are coincide to corresponding to values of the state![]() . i.e.
. i.e.![]() .
.
Every measure ![]() describes distribution elementary particle in physical space of quantum system
describes distribution elementary particle in physical space of quantum system ![]() in the state
in the state![]() .
.
If ![]() -algebra
-algebra ![]() has a unit, then in the space
has a unit, then in the space ![]() with
with ![]() weakly topological structure the set of all state
weakly topological structure the set of all state ![]() is convex compact set and represent convex linear combination of pure states
is convex compact set and represent convex linear combination of pure states ![]() from the set
from the set![]() :
:
![]()
or limit of sequence![]() , where
, where ![]() [2] .
[2] .
This means, that elements of set ![]() are the extreme points of set [2] .
are the extreme points of set [2] .
Because each state ![]() defines a probability measure
defines a probability measure ![]() on couple
on couple![]() , where
, where ![]() is borel
is borel ![]() -algebra therefore it is easy to show, that every
-algebra therefore it is easy to show, that every ![]() represent convex linear combination
represent convex linear combination
![]()
of Dirak measures ![]() where
where ![]() or limit of sequense
or limit of sequense![]() , where
, where ![]() [2] .
[2] .
For every state ![]() we have
we have ![]() therefore it is easy that the value of
therefore it is easy that the value of
quantum state on observable ![]() is the middle value of this observable. The value
is the middle value of this observable. The value ![]() is called the middle value of observable
is called the middle value of observable ![]() of quantum physical system in the state
of quantum physical system in the state![]() .
.
All told above follows that a quantum physical system is an object, so-called statistical structure [4] :
![]() ,
,
where ![]() some
some ![]() -algebra, Hermit element of which are called observables of this system,
-algebra, Hermit element of which are called observables of this system, ![]() is the space of quantum system,
is the space of quantum system, ![]() Borel
Borel ![]() -algebra in
-algebra in![]() ,
, ![]() the probability measure defined by state
the probability measure defined by state ![]() and which describes distribution elementary particle in physical space of quantum system
and which describes distribution elementary particle in physical space of quantum system ![]() in the state
in the state![]() .
.
3. A Stochastic Dynamics of Quantum System
Theorem 2. Every Hermit’s element![]() ,
, ![]() in
in ![]() -algebra
-algebra ![]() defines probability measure on the set of states
defines probability measure on the set of states![]() .
.
Proof: It is well-known that the map ![]() defined by formula
defined by formula ![]() is isometric embedding
is isometric embedding ![]() as Banach space in the double conjugate space
as Banach space in the double conjugate space ![]() [3] . If
[3] . If ![]() is a state then
is a state then ![]() [2] ; it follows that if
[2] ; it follows that if ![]() is positive element, then
is positive element, then ![]() and
and![]() .
.
Thus if ![]() is positive element then
is positive element then ![]() for each state on
for each state on![]() . Because
. Because ![]() is isometric, and therefore
is isometric, and therefore![]() .
.
![]() .
.
If ![]() is hermit’s element
is hermit’s element![]() , because, for such elements
, because, for such elements ![]() and
and
![]() .
.
Let![]() ,
, ![]() be hermit’s positive element in
be hermit’s positive element in![]() , then spectrum
, then spectrum![]() . Let
. Let ![]() be the set of all states on
be the set of all states on![]() , if
, if ![]() is a set of states; we assume the measure
is a set of states; we assume the measure ![]() of this set is
of this set is![]() , if
, if ![]() consists for all such element
consists for all such element ![]() for which
for which ![]()
![]()
![]() Since
Since![]() , 0 and 1 are elements of
, 0 and 1 are elements of ![]() [5] , and
[5] , and
therefore![]() . It is clear that, if
. It is clear that, if ![]() then
then
![]() .
.
If we assume![]() , then we get a measure on
, then we get a measure on![]() .
.
The sets for which we define measure, make ![]() -algebra in
-algebra in![]() . This is not a Borel’s
. This is not a Borel’s ![]() -algebra in space
-algebra in space ![]() whit the
whit the ![]() weekly topology. Denote it by
weekly topology. Denote it by![]() . Thus, we define on
. Thus, we define on ![]() probability measure. The theorem is proved.
probability measure. The theorem is proved.
Consider the family of measures ![]() defined above, where
defined above, where ![]() is the set of positive hermit’s elements whit norm 1,
is the set of positive hermit’s elements whit norm 1, ![]() is corresponding to hermit’s element
is corresponding to hermit’s element![]() ,
, ![]() -algebra in
-algebra in![]() .
.
Let ![]() statistical structure represent a quantum physical system,
statistical structure represent a quantum physical system,![]() . For each
. For each ![]() we can define the measure
we can define the measure ![]() on the set of states
on the set of states ![]() of given quantum physical system such:
of given quantum physical system such:
![]() if
if![]() ,
,![]() .
.
Literally, we have defined measure ![]() on the set of measures
on the set of measures![]() , of which each element
, of which each element ![]() describes distribution elementary particles in physical space
describes distribution elementary particles in physical space ![]() of quantum system in the state
of quantum system in the state![]() .
.
If ![]() is strongly one parametric group of maps of
is strongly one parametric group of maps of ![]() -algebra
-algebra ![]() whit unity and
whit unity and ![]() for all
for all![]() , then following conditions are equivalent [2] :
, then following conditions are equivalent [2] :
1) All ![]() automorphisms of
automorphisms of![]() ;
;
2) ![]() for all
for all![]() ;
;
3) ![]() , where
, where ![]() is the set of positive elements in
is the set of positive elements in![]() ;
;
4) ![]() , for all
, for all![]() .
.
Each defined measure ![]() describes distribution of states in
describes distribution of states in ![]() relatively to middle value of observable
relatively to middle value of observable ![]() over states in
over states in![]() , or distribution of elementary particles in physical space
, or distribution of elementary particles in physical space ![]() of quantum system in the states
of quantum system in the states ![]() relatively to middle value of observable
relatively to middle value of observable ![]() over states in
over states in![]() .
.
It follows: If strongly continuous one parametric group of automorphisms ![]() describes dynamic of structure of observables, according to this, we have a picture of evolution of distribution of states quantum system
describes dynamic of structure of observables, according to this, we have a picture of evolution of distribution of states quantum system ![]() relatively to each observable
relatively to each observable![]() .
.
Such, the representation of quantum physical system as a statistical structure allows formalizing the dynamics of the quantum system as a random process.