1. Introduction
Geometrical optics serves as a powerful tool for investigating optical systems. The path of a light ray is described by an eikonal. When the light rays are paraxial rays, this is classified as linear optics. In this approximation, the propagation of the light ray is described by the product of the refraction and the transfer matrices [1] [2] . Moreover, if the light ray is considered to have rotational symmetry with respect to the optical axis (skewness equal to zero), it is called meridian or Gaussian optics [3] . In this case, the refraction and transfer matrices are expressed by 2 × 2 matrices. The product of these matrices is also represented by a 2 × 2 matrix, and this is called an ABCD-matrix and specifies the optical system.
In this article, we develop the mathematical properties of an affine transformation from the optical and mechanical points of view. Since the affine transformation has a displacement part, we are able to discuss the translation in phase space. Thus, we show that the affine transformation not only distorts but also displaces the Wigner function. Because this displacement can have time dependency, the Wigner function moves dynamically in phase space.
This paper is organized in the following way. In Section 2, we define the affine transformation and show the eikonals which generate this transformation. In Section 3, we turn to the quantum mechanical case for the affine transformation. We show that the operator of the affine transformation is obtained from the product of the displacement operator and the unitary operator of the ABCD-transformation. We also calculate the kernels of the affine transformation. In Section 4, we treat the wavization by referring to the Gabor function. In Section 5, we discuss the affine transformation of the Wigner function. We give an explicit form of the affine transformed Wigner function and examine the change in its configuration and the displacement of the Wigner function. Section 6 is devoted to a summary.
2. Affine Eikonal
The general affine transformation is defined by a linear combination of position q and momentum p with the four parameters A, B, C and D and the displacements for position E and momentum F. We define the affine transformed position Q and momentum P as
 , (1a)
, (1a)
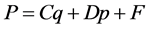 , (1b)
, (1b)
with the lossless (area-preserving or power-preserving) condition
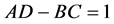 . (2)
. (2)
In classical mechanics, this condition comes from which affine transformation 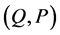 satisfies the Poisson bracket (PB)
satisfies the Poisson bracket (PB)
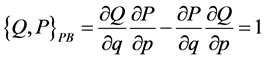 , (3)
, (3)
that is, Q and P are canonical variables [8] .
In geometrical optics, the path of the light ray is described by an eikonal. In the following discussion, we restrict ourselves to Gaussian optics, so each q and p is one- dimensional variable. There are four types of eikonal in Gaussian optics. We list the four types below;
 for point eiknal, (4a)
for point eiknal, (4a)
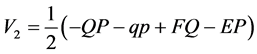 for mixed eikonal, (4b)
for mixed eikonal, (4b)
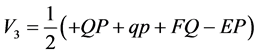 for mixed eikonal, (4c)
for mixed eikonal, (4c)
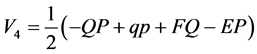 for angle eikonal. (4d)
for angle eikonal. (4d)
By substituting (1) into (4), we rewrite these eikonals in terms of two of the four canonical variables q, p, Q and P,
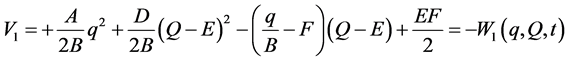 (5a)
(5a)
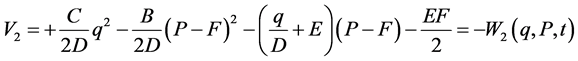 (5b)
(5b)
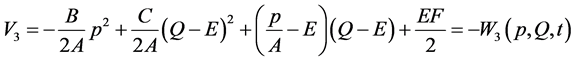 (5c)
(5c)
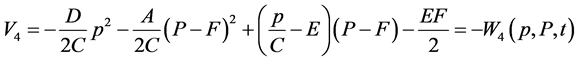 (5d)
(5d)
These four functions  are sometimes called eikonals [3] . Because of the relationship between optics and mechanics, we prefer to call them generating functions [8] , and these generate the affine transformation (1) by differentiation with respect to the canonical variables as follows,
are sometimes called eikonals [3] . Because of the relationship between optics and mechanics, we prefer to call them generating functions [8] , and these generate the affine transformation (1) by differentiation with respect to the canonical variables as follows,
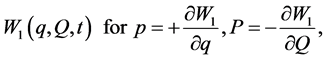 (6a)
(6a)
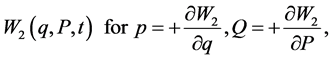 (6b)
(6b)
 (6c)
(6c)
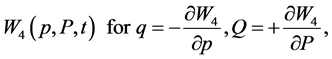 (6d)
(6d)
We listed four types of the generating functions in (5). From the theoretical and experimental points of view, it sometimes happens that we cannot describe the affine transformation via one of them. For example, the affine transformation in (20) below has zero component in![]() . In that case, we cannot use (5d), but the other ones are available. The relationship between these eikonals (generating functions) is depicted in Figure 1. The functions at the ends of the arrows are related to each other by a Legendre transformation. For example, from the relation (6a), we obtain the variable Q in terms of q and P,
. In that case, we cannot use (5d), but the other ones are available. The relationship between these eikonals (generating functions) is depicted in Figure 1. The functions at the ends of the arrows are related to each other by a Legendre transformation. For example, from the relation (6a), we obtain the variable Q in terms of q and P,
![]() .
.
Substituting this relation into (5a) and![]() , we obtain (5b).
, we obtain (5b).
3. Kernel of the Affine Transformation
In this section, we consider the quantum mechanical version of the affine transformation.
![]()
Figure 1. The eikonals (generating functions) are disposed on the corners of the square. The functions at the ends of arrows are related to each other by a Legendre transformation.
Corresponding to the canonical transformation in classical mechanics, the unitary transformation plays a central role in quantum mechanics. Analogous to the classical affine transformation (1), we define the quantum mechanical affine transformation as follows,
![]() , (7a)
, (7a)
![]() , (7b)
, (7b)
where ![]() describes the q-number and
describes the q-number and ![]() is a unitary operator which generates the affine transformation. Here,
is a unitary operator which generates the affine transformation. Here, ![]() is also needed when the canonical commutation relations
is also needed when the canonical commutation relations ![]() are satisfied.
are satisfied.
To obtain the unitary operator![]() , we introduce two operators. One is the displacement operator
, we introduce two operators. One is the displacement operator![]() ,
,
![]() (8)
(8)
which generates the displacements in position and momentum,
![]() , (9a)
, (9a)
![]() . (9b)
. (9b)
The other one is the unitary transformation![]() ,
,
![]() (10)
(10)
which generates the ABCD-transformation [9]
![]() , (11a)
, (11a)
![]() , (11b)
, (11b)
where
![]() , (12)
, (12)
and![]() . Note here that when we assign
. Note here that when we assign
![]() (13)
(13)
then ![]() describes the squeezed operator [10] .
describes the squeezed operator [10] .
We consider the unitary operator![]() , which generates the quantum affine transformation (7), as a product of
, which generates the quantum affine transformation (7), as a product of ![]() and
and![]() ,
,
![]() . (14)
. (14)
Indeed, we obtain
![]() , (15a)
, (15a)
![]() , (15b)
, (15b)
which is the quantum mechanical affine transformation (7) as we expected.
Now, we calculate the kernel of the affine transformation. The kernel is just the transition amplitude from the position q at an initial time to the position Q at a later time given by![]() . To obtain the kernel, we use the coordinate identity operator
. To obtain the kernel, we use the coordinate identity operator ![]() between the displacement operator
between the displacement operator ![]() and the unitary operator
and the unitary operator![]() :
:
![]() (16)
(16)
Using the formulae
![]() , (17a)
, (17a)
![]() , (17b)
, (17b)
we obtain
![]() (18)
(18)
Substituting the transition amplitude in terms of ![]() [9] , we obtain the result:
[9] , we obtain the result:
![]() . (19)
. (19)
We include the “irrelevant” constant phase factor which has often been neglected in the literature [11] [12] . The function in the exponent is in the same form as that of the generating function (5a). For example, let us consider a particle with mass m, subjected to a constant external force f, moving from ![]() to
to ![]() in time t. The exact solution for this problem is described in the following,
in time t. The exact solution for this problem is described in the following,
![]() . (20)
. (20)
Substituting these parameters into (19), we obtain
![]() , (21)
, (21)
which is the same equation as that obtained from the path integral [13] .
The other kernels are derived in the same manner. We list all four types of transition amplitude below:
![]() , (22a)
, (22a)
![]() , (22b)
, (22b)
![]() , (22c)
, (22c)
![]() , (22d)
, (22d)
where the W’s in the exponentials are the generating functions (5) which generate the canonical transformation (1).
It is worth commenting here that it is well known in classical mechanics [8] that the generating functions (5) are related to each other by a Legendre transformation (Figure 1), whereas the kernels (22) are related to each other by a Fourier transformation. These relations are depicted in Figure 2.
4. Wavization of Gabor Function
Quantum mechanics is obtained by the “quantization” of classical mechanics. Similarly, physical optics is constructed by the “wavization” of geometrical optics [3] [6] . The famous example is that of Fraunhofer diffraction obtained by wavization of a plain wave. Let us consider the Gabor function [6] [14] ;
![]() , (23)
, (23)
where ![]() is the wave number and
is the wave number and ![]() is the center of this wave packet. The
is the center of this wave packet. The
![]()
Figure 2. The kernels are disposed on the corners of the square. The functions at the ends of arrows are related to each other by a Fourier transformation.
width is obtained from
![]() . (24)
. (24)
To make the calculation easier, this wave packet (23) can be rewritten in the form,
![]() , (25)
, (25)
with![]() . Note that when
. Note that when![]() , it gives the position-representation
, it gives the position-representation
of the coherent state wave function![]() . It is also worth writing down the Fourier transformation of (23) and (25),
. It is also worth writing down the Fourier transformation of (23) and (25),
![]() , (26)
, (26)
![]() . (27)
. (27)
Using this expression, we obtain ![]() and the width
and the width
![]() . (28)
. (28)
This result with (24) gives
![]() , (29)
, (29)
that is, the Gabor function satisfies the minimum uncertainty relation.
We obtain the affine transformation of the Gabor wave packet by using the kernel (22),
![]() (30)
(30)
and
![]() (31)
(31)
where we introduce two complex variables,
![]() , (32a)
, (32a)
![]() . (32b)
. (32b)
Having the probability density from (30) and (31), we obtain
![]() , (33a)
, (33a)
![]() . (33b)
. (33b)
The center of the Gabor function propagates along the affine transformation (1). From these Equation (33), we obtain the variances
![]() , (34a)
, (34a)
![]() , (34b)
, (34b)
and the uncertainty relation
![]() . (35)
. (35)
Since the only constraint for the parameters ![]() is
is![]() , these parameters have time dependency. So, these results (34) and (35), show the time development of the variances and the uncertainty relation of the Gabor function.
, these parameters have time dependency. So, these results (34) and (35), show the time development of the variances and the uncertainty relation of the Gabor function.
Let us show two examples here. As we saw in (25), the Gabor function with ![]() signifies a coherent state. So, using (13) as
signifies a coherent state. So, using (13) as![]() , (35) becomes
, (35) becomes
![]() , (36)
, (36)
which coincides with the uncertainty relation of the squeezed state [10] . The other example is where we use (20), then (35) becomes
![]() , (37)
, (37)
which coincides with the uncertainty relation [15] of the spreading of the Gaussian wave packet in time.
5. Affine Transformation of the Wigner Function
The Wigner function [16] - [18] is widely used in studying optics and the correspondence between classical and quantum mechanics [6] [7] . The Wigner function for any wave function ![]() is defined by
is defined by
![]() . (38)
. (38)
When we take a Gabor function (23) for any wave function![]() , the Wigner function (38) becomes
, the Wigner function (38) becomes
![]() . (39)
. (39)
Now we apply the unitary operator ![]() to any wave function;
to any wave function;![]() . We obtain the affine transformation of the Wigner function,
. We obtain the affine transformation of the Wigner function,
![]() . (40)
. (40)
To cast the right hand side, we use the coordinate identity operator ![]() twice,
twice,
![]() . (41)
. (41)
Substituting the kernel (22a) into (41) and integrating over u, we obtain
![]() (42)
(42)
where ![]() is a delta function of z. Changing the variables
is a delta function of z. Changing the variables ![]() and
and![]() , we obtain
, we obtain
![]() (43)
(43)
where we use the formula![]() . Integrating over
. Integrating over![]() , we obtain
, we obtain
![]() , (44)
, (44)
where we use ![]() and change the variable
and change the variable![]() . This is the affine transformation of the Wigner function which is a generalization of (38) and can be applied to any wave function
. This is the affine transformation of the Wigner function which is a generalization of (38) and can be applied to any wave function ![]() and to any affine transformation with the condition AD ? BC = 1. Equation (44) shows that the ABCD-part describes the area-preserving distortion, and the E, F-part describes the displacement in phase space. It is permissible for any affine transformation to have time dependency, so we are able to investigate the dynamic properties of the Wigner function in phase space.
and to any affine transformation with the condition AD ? BC = 1. Equation (44) shows that the ABCD-part describes the area-preserving distortion, and the E, F-part describes the displacement in phase space. It is permissible for any affine transformation to have time dependency, so we are able to investigate the dynamic properties of the Wigner function in phase space.
As an example of a wave function![]() , we take a Gabor function. Substituting the Gabor function (23) into (44) and integrating over u, we obtain
, we take a Gabor function. Substituting the Gabor function (23) into (44) and integrating over u, we obtain
![]() . (45)
. (45)
This equation is a generalization of (39), that is, in its initial state, the Wigner function of the Gabor function is represented by (39). Once the affine transformation switches on, the Wigner function changes along with (45). Note that integrating (45) over P and Q respectively, we recover (33);
![]() , (46a)
, (46a)
![]() , (46b)
, (46b)
which is the correct character of the Wigner function.
6. Summary
We have developed the mathematical properties of an affine transformation from the optical and mechanical points of view. The kernels of the affine transformation were clearly derived and comprise the eikonals (generating functions) which generated the affine transformation in optics (mechanics).
Using the kernel, we discussed the wavization of the Gabor function. The Gabor function has a Gaussian profile and is symmetric in position and momentum. We found the time development of the uncertainty relation, according to the affine transformation.
We also discussed the affine transformation of the Wigner function and showed not only the distortion but also the dynamic movement of the Wigner function in phase space.