Time of the Energy Emission in the Hydrogen Atom and Its Electrodynamical Background ()
1. Introduction
In physics, we often look for a simple explanation of the important phenomena without going much into details of the examined process. A well known example is the energy spectrum of the hydrogen atom. The first step to approach this spectrum theoretically was based on the idea that the force of the electrostatic attraction existent between the electron particle and the atomic nucleus remained in an equilibrium with the centrifugal force due to the circular electron motion about the same nucleus [1] . The second decisive step was that the angular momentum which accompanied the motion leading to the equilibrium of the atomic system should be quantized in a proper way. A combination of these two steps gave a spectacular success of the Bohr atomic model expressed in terms of positions of the electron energy levels present in the atom.
But the point not examined in the Bohr theory was the transition time between different quantum levels necessary to obtain the energy spectrum effect. A kind of paradox becomes that if we have two quantum states in the atom, say a hydrogen atom, their energies are well known, and the same knowledge applies naturally to the energy difference
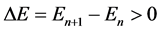 (1)
(1)
between the states n + 1 and n entering the transition process, but we cannot answer how long is the time interval Δt necessary to perform such transition. Certainly, the interval Δt is classified as “short” but no quasi-definite answer on its size is in practice available.
A reason of such situation cannot be the so-called uncertainty principle between the intervals of energy and time introduced by Heisenberg [2] [3] . In fact, this principle concerns rather a mutual relation between two definite and accessible intervals ΔE and Δt entering a given quantum process than an “uncertainty” of the accuracy which can be attained in the measurement of the sizes of the mentioned intervals [4] - [6] . This implies that there does not exist an a priori difficulty to obtain Δt when ΔE is known.
The main source of difficulty to calculate Δt seems to be a probabilistic- and statistical character of examination applied in the treatment of the electron transitions. This kind of approach, being typical for the old quantum theory [7] [8] , obtained its farther background in the formalism of quantum mechanics [3] [9] [10] . In effect the results for Δt connected with the electron transition obtained respectively by the classical and quantum-mechanical approaches became diametrically different [10] . For, in order to obtain an agreement with the transition intensity of energy provided by the quantum-mechanical theory, the classical approach to that intensity required the time interval Δt of an infinite size, viz.
 (2)
(2)
instead of a finite (small) Δt dictated evidently by an experimental practice.
In a set of papers [11] - [15] , we tried to approach the size of Δt with the aid of an examination of the electron transitions in small quantum systems with the aid of the Joule-Lenz law; see e.g. [16] [17] . For transitions connected with the population change of the neighbouring energy levels, i.e. n + 1 and n, the main result was that the relation
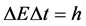 (3)
(3)
should be satisfied. In the case of the harmonic oscillator
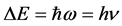 (4)
(4)
where
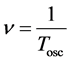 (5)
(5)
is the oscillator frequency of the emitted electromagnetic wave and 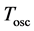 is the time period of that wave. In effect we obtain with the aid of (3)-(5):
is the time period of that wave. In effect we obtain with the aid of (3)-(5):
 (6)
(6)
or
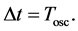 (7)
(7)
Because of (3) the emission intensity of a single wave having the frequency  becomes
becomes
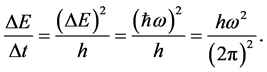 (8)
(8)
The intensity (8) can be referred to the the quantum-mechanical expression for the transition intensity of the harmonic oscillator [10]
 (9)
(9)
by the formula
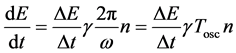 (10)
(10)
where
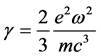 (11)
(11)
is the damping term of the oscillator and 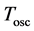 is the time period presented in (5); see also [10] .
is the time period presented in (5); see also [10] .
2. The Aim of the Paper
The aim of the present paper is to examine in some detail the transition time Δt between the neighbouring quantum levels of the hydrogen atom. Certainly the size of Δt, because of its expected very short duration, seems to be hardly possible to be compared accurately with the experimental data. Nevertheless, an idea how Δt can be influenced by the electrodynamical parameters responsible for the electron transition could be given. This makes, in principle, the problem of the time transfer Δt between two quantum states reduced to a semiclassical one, so it can be treated with the aid of the classical electrodynamics. Before the electrodynamical properties will be discussed it seems of use to get an insight into the quantum aspects of Δt based on the Joule-Lenz law.
3. Electron Transition Time Obtained from the Joule-Lenz Law
A preliminary approach to the time transfer of energy in the hydrogen atom, but not only in such system, can be done with the aid of a quantum insight into the Joule-Lenz law; see [11] - [15] . The dissipation rate of the energy ΔE within the time interval Δt can be expressed by the formula
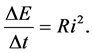 (12)
(12)
Here the R and i are respectively the resistance and current intensity of the electron transition process done in course of Δt. The process leads to the energy dispense (decrease) equal to ΔE.
For an unmodified (stationary) electron motion in the atom the current intensity is a constant
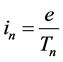 (13)
(13)
for any quantum state n because of a constant time period Tn representing the circulation of the electron charge e about the nucleus [18] :
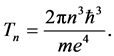 (14)
(14)
Certainly in course of the transition from one orbit, say that of the quantum state n + 1, to the orbit of state n, the intensity is modified from in+1 to in, but in fact the change of i is not large, especially when . Therefore, we can assume that
. Therefore, we can assume that
![]() (15)
(15)
The potential V entering the electric resistance
![]() (16)
(16)
let be
![]() (17)
(17)
where in the numerator is substituted the energy difference between quantum states presented in (1). For large n, the energy ΔE becomes [18] :
![]() (18)
(18)
By combining Vn in (17) with in calculated from (13) and (14), we obtain the resistance
![]() (19)
(19)
independent of the state n. The resistance R obtained in (19) is characteristic for the integer quantum Hall effect [19] . The whole fraction (12) becomes
![]() (20)
(20)
where in the last step we applied for ΔE the result of (18) obtained from large n.
In effect, Δt attains the value
![]() (21)
(21)
which is formally equal to the size of the time period Tn given in (14).
In the next step, by multiplying the both sides of (21) by ΔE taken from the final step of (18) we obtain
![]() (22)
(22)
This is a result providing us with a very simple relation between the ΔE and Δt.
The relation identical with (3) has been rather extensively applied in comparing the quantum-mechanical spectrum of transition probabilities between the electron states in the hydrogen atom [20] [21] with the intensity of the electron transitions calculated with the aid of ΔE and Δt entering the formula (22), i.e. the formula
![]() (23)
(23)
similar to (8) for the oscillator has been applied; see [11] - [15] . More precisely, the formula (23) is valid solely for transitions
![]() (24)
(24)
but the transition time Δt corresponding, say, to situations
![]() (25)
(25)
etc, can be composed from the Δt calculated for the case of (23) [13] [14] .
Another important point concerning Δt in (23) is its reference to the time period T of the electromagnetic wave produced by the energy difference ΔE. In fact because of the result
![]() (21a)
(21a)
obtained in (21), the formula (23) becomes reduced to
![]() (26)
(26)
therefore we obtain
![]() (27)
(27)
which is similar to (7) for the harmonic oscillator.
In fact, the formulae (23) and (27) are not specific solely for the hydrogen atom and the harmonic oscillator, but their validity can be extended to other quantum systems, for example the particle in a one-dimensional potential box; see [11] [12] [15] . Because of (21) and (27), we obtain also
![]() (27a)
(27a)
In fact on the basis of of (14), we have
![]() (27b)
(27b)
In the last step of (27b) the result obtained in (18) has been taken into account.
The aim of the remainder of the paper is to show―for the hydrogen atom taken as an example―that the result of (26) obtained mainly on a quantum footing―could find its correspondence also in effect of a semiclassical approach to the electron transition.
4. Electrodynamical Parameters Connected with the Electron Transition and Its Current
First of the necessary parameters will be the magnetic flux ![]() and its changes in the atom due to the changes of the population of the quantum levels [15] . The magnetic field Bn connected with the quantum state n is an effect of the electron circulation along the orbit n. This implies that Tn in (14) and the time period causing the existence of Bn should be equal. Therefore (see e.g. [22] [23] )
and its changes in the atom due to the changes of the population of the quantum levels [15] . The magnetic field Bn connected with the quantum state n is an effect of the electron circulation along the orbit n. This implies that Tn in (14) and the time period causing the existence of Bn should be equal. Therefore (see e.g. [22] [23] )
![]() (28)
(28)
where the field B is directed normally to the orbit plane.
A substitution of Tn from (14) into (28) gives the relation
![]() (29)
(29)
from which
![]() (30)
(30)
The magnetic flux across the area of a circular orbit having the radius [18]
![]() (31)
(31)
is equal to
![]() (32)
(32)
because the area enclosed by the orbit amounts to
![]() (33)
(33)
on condition the radius rn in (31) is taken into account.
Evidently the absolute change of ![]() associated with the change of n by
associated with the change of n by
![]() (34)
(34)
provides us for any n with the value
![]() (35)
(35)
This is a quantum a) independent of n, b) well-known from the physics of supe- conductors [23] - [25] . Let us note that if
![]() (35a)
(35a)
is the Bohr magneton [3] , the formula (35a) multiplied by ![]() and divided by the flux in (35) gives
and divided by the flux in (35) gives
![]() (35b)
(35b)
which is a distance known as the radius of the electron microparticle; see e.g. [17] .
In fact the steady orbital current in+1 is perturbed in course of transition from n + 1 to n, nevertheless we expect this perturbation is small. The effective current of transition let be
![]() (36)
(36)
where solely
![]() (37)
(37)
is the current part dependent on time t. Assuming that the orbits system between states n + 1 and n behaves like a condenser, our idea is to introduce a current
![]() (38)
(38)
representing a discharge of the condenser [17] [26] . This
![]() (39)
(39)
enters (36) and (37).
The interval ![]() in (35) is coupled with the self-induction constant L by the formula
in (35) is coupled with the self-induction constant L by the formula
![]() (40)
(40)
but the differentiation process with respect to time concerns solely the term id:
![]() (41)
(41)
The resistance R is
![]() (42)
(42)
and the capacitance C for a planar condenser is
![]() (43)
(43)
But because of a cylindrical shape of the orbits forming the condenser the formula (36) should be replaced by [26]
![]() (44)
(44)
The L, R and C parameters enter the time-dependent differential equation for the current id in (36) (see [17] ):
![]() (45)
(45)
where ![]() is the applied electromotive force. If we assume that
is the applied electromotive force. If we assume that
![]() (46)
(46)
where
![]() (47)
(47)
the solution of (45) becomes
![]() (48)
(48)
the e in (46) and (48) is the basis of the natural logarithms.
On condition we assume that
![]() (49)
(49)
the differential process of (45) performed upon (48) gives
![]() (50)
(50)
The solution of (50) leads to the frequency [17] [26] :
![]() (51)
(51)
5. Calculation of the Frequency w
From Equation (40), we have
![]() (52)
(52)
because of (35), so in view of (44):
![]() (53)
(53)
In the next step from (42) and (52)
![]() (54)
(54)
Therefore, (51) becomes
![]() (55)
(55)
Since
![]() (56)
(56)
we have
![]() (57)
(57)
so the expression entering the square root in (55) is equal to
![]() (58)
(58)
In effect ![]() in (51) becomes equal to the imaginary value
in (51) becomes equal to the imaginary value
![]() (59)
(59)
This result gives for the current in (48) the formula
![]() (60)
(60)
With e in (60) being the basis of natural logarithms, we obtain for id a current exponentially decreasing with time t.
Let us note that when R = 0, which is the case where no resistance does exist for the transition current, the expression for ![]() becomes [see (51)]:
becomes [see (51)]:
![]() (61)
(61)
in virtue of (57).
6. Emission Rate and Its Damping Time
On the basis of (20) and (21), it is easy to calculate the emission rate
![]() (62)
(62)
By substituting for simplicity ![]() and
and![]() , we obtain
, we obtain
![]() (63)
(63)
This is a very high number especially for small n, nevertheless it is valid solely at the very beginning of the emission process. The duration of that process for the energy interval ΔE is approximately equal to [see (21)]:
![]() (64)
(64)
7. Velocity of the Electron Transition between Two Neighbouring Quantum Levels
The result of (21) and (26) allows us to calculate the velocity of transition of the electron particle between the levels n + 1 and n. This is
![]() (65)
(65)
where [see (31)]
![]() (66)
(66)
With ΔE represented by a difference in the kinetic electron energy
![]()
this gives
![]() (67)
(67)
We find that the transition velocity of the electron between levels n + 1 and n is by a factor of ![]() smaller than the velocity
smaller than the velocity ![]() along the orbit n. This calculation is fully original and new.
along the orbit n. This calculation is fully original and new.
8. Comments
Heisenberg strongly criticized the Bohr atomic model as useless because it applied the unobserved elements of the atomic structure like the electron orbits; see e.g. [26] - [28] .
Nevertheless the combined orbital parameters, like the orbit radius or orbit length and the time period of the electron circulation, allowed us to approach correctly the parts of the electron kinetic and potential energy which―when added together―gave a proper total electron energy in the atom. This energy formula has been next confirmed by both the modern quantum theory (quantum mechanics) and experiment.
But the modern theory did not provide us with an adequate information on the time duration of the electron processes in the atom, for example the time of the electron transitions. In this circumstance, a step towards the old quantum theory which applied definite periods of time seemed to be both realistic and useful.
In the first step, we assumed that the classical Joule-Lenz theory can couple the amount of energy emitted in the quantum process of an electron transition with the time necessary for that process. This assumption led to an extremely simple relation between the emitted energy ΔE and emission time Δt. In the present paper our aim was to approach the time necessary for the emission of ΔE on a somewhat different way than a direct application of the Joule-Lenz law, i.e. mainly with the aid of a classical analysis of the electric current produced as an effect of transition giving the energy change ΔE.
In the first step of this analysis, the quanta of the magnetic induction and magnetic flux are introduced to the formalism. It should be noted that the Bohr magneton divided by the quantum change of the magnetic flux between the neighbouring levels [see (35b)] gives the well-known formula for the radius of the electron microparticle; see e.g. [17] . An earlier derivation of (35b)―different only in a constant factor―has been done in [29] ; see also [30] .
Next the electric current connected with the transition between two neighbouring quantum levels is considered as due to a discharge of the condenser. In order to examine this current, the costants of self-induction, resistance and capacitance characteristic for such condenser have been calculated. In effect an exponential decrease of the time-dependent part of the discharge current is obtained; see (60).
A very simple approach to the discharge current from state n can be attained when the Ohm’s law is applied [21] :
![]() (68)
(68)
Here Q = e and −dQ = de is a small decrease of charge of the condenser in a small time interval dt. The formula (68) gives
![]() (69)
(69)
Therefore
![]() (70)
(70)
because
![]() (71)
(71)
Hence the charge Q decreases with t according to the formula
![]() (72)
(72)
The exponent of the natural logarithm basis e in (72) is a half of that obtained in (60). The rate of the emission in the form of the electromagnetic field energy has been discussed in [31] .
It can be noted that Equations (3) and (22) are formally similar to the inequality proposed by Heisenberg called the uncertainty principle for energy and time. In fact the physical background for the intervals ΔE and Δt entering he Heisenberg principle is much different than the properties of the intervals Δpx and Δx, concerning―for example―the x-coordinates of the momentum and position of a particle. For, contrary to the momenum and position, the energy E can be measured to any degree of accuracy at any instant of time. Therefore ΔE can be the difference between two exactly measured values of energy at two different instants; see [4] - [6] .
9. Conclusions
The paper approaches a seldom discussed problem of an individual electron transition between two quantum levels in the hydrogen atom. Consequently, no reference has been done to the well-known probabilistic theory usually applied to the quantum transitions.
In the first step, the emission time of energy between two neighbouring levels in the atom is calculated on the basis of the quantum aspects of the Joule-Lenz law; see (21) and (22). This time is found equal to the oscillation period of the electromagnetic wave emitted in course of the transition process; see (27).
Next, the problem of the emission was approached with the aid of the classical electrodynamics by assuming that the electron transition in the atom was roughly equivalent to a discharge of an electrical condenser. The damping time of the current obtained in course of such discharge is found to be close to the transition time attained in the Joule-Lenz theory; see (60) and (61), as well as (72) for the case of a simplified treatment of the calculation.
By assuming that the transition time between the quantum levels is similar to the emission time, the velocity of transition of the electron particle between the neighbouring orbits in the atom has been estimated; see (67).
A by-product of the calculations is the result that the Bohr magneton divided by the quantum of the magnetic flux obtained from the flux difference of two energy levels in the atom approaches the geometrical radius attributed to the electron microparticle; see (35a) and (35b).