Domain Decomposition for Wavelet Single Layer on Geometries with Patches

Maharavo Randrianarivony

Pappelweg 7, Zimmer 21, Sankt Augustin, Germany.

DOI: 10.4236/am.2016.715151                

Abstract

We focus on the single layer formulation which provides an integral equation of the first kind that is very badly conditioned. The condition number of the unpreconditioned system increases exponentially with the multiscale levels. A remedy utilizing overlapping domain decompositions applied to the Boundary Element Method by means of wavelets is examined. The width of the overlapping of the subdomains plays an important role in the estimation of the eigenvalues as well as the condition number of the additive domain decomposition operator. We examine the convergence analysis of the domain decomposition method which depends on the wavelet levels and on the size of the subdomain overlaps. Our theoretical results related to the additive Schwarz method are corroborated by numerical outputs.

Keywords

Wavelet, Single Layer, Patch, Domain Decomposition, Convergence, Graph Partitioning, Condition Number

1. Introduction

Integral equation simulations have useful applications in synthetic medical design and molecular docking. The challenges to be confronted when treating a BEM (Boundary Element Method) simulation are multiple. First, the resulting BEM-matrix is dense if classical polynomial basis functions are used. Second, the matrix entries are usually integrals admitting 4D integrands which are singular. In addition, the matrix density results in a large memory capacity requirement which leads to the need of a dense linear solver for standard polynomial bases. On the other hand, the advantage of BEM [1] - [5] over the traditional FEM (Finite Element Method) [6] - [8] is that one needs only smaller geometric data [9] because light-weight 2D-surfaces are utilized instead of massive 3D-meshes. That is especially true if one is only interested in the solution on the surface of a given geometry or in the infinite domain exterior to the geometry as frequently occurring in quantum simulations. In addition, the convergence is substantially faster because only a small degree of freedom is sufficient to attain a precise BEM approximation. Wavelets [1] [10] - [12] partially serve as a remedy to the former challenges as they compress the dense matrices into quasi-sparse ones [13] - [16] . In the BEM framework, there are generally two formulations (first kind and second kind) which have their own advantages and drawbacks. The first kind formulation admits a weakly singular kernel while the second one admits a double layer kernel. Therefore, the computation of the integrals for the first kind is comparatively more efficient. On the other hand, the first kind formulation produces a system which is badly conditioned as the condition number escalates exponentially with the wavelet levels. In contrast, the second kind formulation produces a system which admits a bounded condition number if the multiscale wavelet basis is used. The purpose of this document is to remedy the bad conditioning of the first kind formulation. We will use domain decomposition techniques [17] - [19] to overcome that bad conditioning of the weakly singular BEM. That amounts to decomposing the whole surface into subdomains which are overlapping in our case. Each subdomain will be an amalgamation of surface patches. We will utilize only the additive version of the domain decomposition which is thus equivalent to a block Jacobi structure. The width of the subdomain overlaps will play an important role in the convergence guarantee of the additive domain decomposition. A graph decomposition into subgraphs is applied to carry out the domain decomposition in practice. Before going into details, a short survey of related past works is in order. A splitting method for CAD surfaces has been proposed in [20] for BEM simulation. Additionally, methods for checking the regularity of the mappings have been proved in [21] . While approximations are required to obtain global continuity in [21] [22] for CAD objects, it can be achieved exactly for molecular surfaces in [23] [24] . Furthermore, a real chemical simulation by using wavelet BEM is described in [25] for the quantum computation. The surface structure which is required by the wavelet-BEM is unfortunately very complicated to construct in contrast to the standard mesh generation [26] . Domain decomposition of BEM using triangular meshes is found in [2] which is also important because many valuable surface geometries (e.g. from 3D-scanner) are only available in triangular forms. Apart from additive methods, multiplicative ones are treated in [4] where planar four-sided patches are utilized. Besides, multigrids [27] - [29] propose an efficient method to alleviate the bad conditioning of linear systems originating from partial differential equations and integral equations. The use of multigrid for the treatment of pseudo-differential operators of order minus one has been examined in [28] which is applicable to weakly singular kernels.

1.1. Principal Contributions

We want to highlight here our main contributions in the theoretical and practical significances. We elaborate mathematical proofs which guarantee the convergence of the additive Schwarz method. For a decomposition 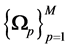of the surface, the ASM operator is used together with the single layer bilinear form. Our first contribution consists in the theoretical estimation of the smallest eigenvalue of the domain decomposition method. That is, for an arbitrary 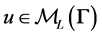on the maximal level L, there is satisfying the representation

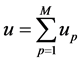
such that the single layer bilinear form 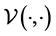fulfills

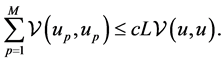
The significance of the above upper bound is that the ASM operator with respect to the weakly singular bilinear form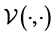

verifies on the maximal level L the eigenvalue lower bound

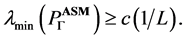
Our next contribution is the theoretical estimation of the largest eigenvalue of the domain decomposition method. The involvement of the overlap size 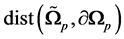of the subsurfaces in the condition number is analytically examined. For an arbitrary function, we have

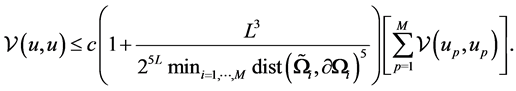
That is significant in deducing the upper estimate

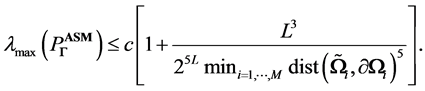
The main significance of this study is to provide a rigorous preconditioner which is theoretically demonstrated to reduce the condition number. We have an analytical deduction of the condition number which does not grow exponentially with the multiscale level. Indeed, the condition number admits the upper bound

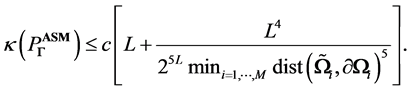
As for the practical contribution, we present outcomes from computer implementations which originate from molecular patches. We use realistic geometries consisting of molecular surfaces on our domain decomposition. The implementation is complete and not just some part of the theory is illustrated. In particular, the BEM linear system as well as the domain decomposition technique has been implemented completely. We contribute in practically exhibiting that the domain decomposition method admits a significant advantage over the unpreconditioned system. A lot of reduction of the iteration number is achieved. By growing the multiscale levels, the required iteration counts grow only very slowly in contrast to the unpreconditioned system whose iteration counts increase significantly fast. In addition, we contribute in utilizing a graph based approach to practically assemble the domain decomposition for the BEM application.

1.2. Advantage over Previous Works

We will describe now the principal advantages of our approach compared with previous methods. An incomplete Cholesky factorization has been recently used in [30] for the preconditioning of the BEM linear system. The principal advantage of the domain decomposition over the Cholesky factorization is that the subproblems (see later (62)) in the additive Schwarz method can be solved independently. As a consequence, if a multiprocessor or a parallel computer is at disposition, the subproblems involving 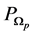can be solved simultaneously by different processors. That is, solving the subproblems requires no interprocessor communications. In contrast, the Cholesky factorization must be solved as a single large entity at once.

A reverse Schur preconditioning technique for use in hierarchical matrices has been newly described in [31] . Hierarchical matrices are entirely other techniques for treating BEM. Their method is fundamentally different from wavelet method because they already take another approach from the starting setup by using meshes in addition to polynomial bases which are very well suited for triangular meshes. The H-matrix method is based on approximation of the integral kernels. The advantage of our method is that we use the original form of the kernels. In addition, the patchwise geometric structure here fits well with domain decompositions which can be applied to distributed computing.

In term of domain decompositions [17] [19] , our presented method is somewhat innovative in the application of additive method to wavelet BEM for free-form curved patches because the currently available methods in domain decompositions are well developed only for finite element method and finite volume method. In the framework of BEM, the domain decomposition techniques are mostly restricted to polynomial bases. Domain decompositions on four-sided patches have been utilized in [4] but they considered only planar patches admitting edges which are parallel to the axes. We are not aware of any more recent generalization of [4] to curved patches. A direct comparison is somewhat difficult because our geometric patches form closed and free-form NURBS manifolds. In addition, they use standard polynomial basis. An advantage of the presented method here is that we use wavelet basis which yields a quasi-sparse linear system that enables faster matrix-vector multiplications. It is beyond the scope of this document to reproduce all the programming tasks that the other authors had implemented for their own approach. Therefore, we base our work on rigorous mathematical theory while the computer results are mainly for illustrative purpose to practically exhibit the remedy of the problem of exponential condition number.

2. Weakly Singular Integral on Patched Manifold

This section is occupied by the presentation of the integral equation of first kind which is formulated on a boundary surface 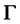that is decomposed into four-sided patches. After presenting the required surface structure, we will introduce the problem setting as well as the variational formulations using a nested sequence of subspaces. We suppose the geometry satisfies the following conditions.

・ We have a covering of the surface by four-sided patches,

・ The intersection of two different patches and is supposed to be either empty, a common curvilinear edge or a common vertex,

・ Each patch where is the image by which is described by a bivariate function that is bijective, sufficiently smooth and admitting bounded Jacobians,

・ The patch decomposition has a global continuity: for each pair of patches, sharing a curvilinear edge, the parametric representation is subject to a matching condition. That is, a bijective affine mapping exists such that for all on the common curvilinear edge, one has. In other words, the images of the functions and agree pointwise at common edges after some reorientation,

・ The manifold is orientable and the normal vector is consistently pointing outward for any.

An illustration of the above surface structure is depicted in Figure 1. The CAD representation of the former mappings uses the concept of B-spline and NURBS [20] [32] [33] . Consider two integers such that. The interval [0,1] is subdivided by a knot sequence such that for and such that the initial and the final entries of the knot sequence are clamped and. One defines the B-splines [32] [34] [35] basis functions as

where we employ the divided difference in which we use the truncated power functions given by if, while it is zero otherwise. The integer k controls the polynomial degree of the B-spline which

Figure 1. Patch representation of a Water Cluster with 1089 NURBS.

admits an overall smoothness of while the integer n controls the number of B-spline functions for which each B-spline basis is supported by. The NURBS patch admitting the control points and weights is expressed as

(1)

We will consider only geometries which are globally smooth and which admit moderate curvature. For each patch, the Gram determinant is denoted by

(2)

After transformation onto, the -scalar product and -norm are expressed respectively as

(3)

Upon the whole surface, we use the Sobolev semi-norm

(4)

We will use the next Sobolev space on the manifold

(5)

where

(6)

We introduce also the dual space equipped with the dual norm

(7)

By designating the 3D region enclosed within by, our objective is to solve the next interior problem with Dirichlet boundary condition for a given:

(8)

We make now the change of unknown by using the density function

(9)

Introduce the single layer operator such that for

(10)

The continuous problem is to search for such that

(11)

Once the solution u to the integral Equation (11) becomes available, the solution to the initial problem (8) is obtained by applying (9). For the discrete Galerkin variational formulation, we consider a nested set of finite dimensional spaces

(12)

whose construction will be specified later on. By discretizing (11) in each subspace, one has such that

(13)

which is a boundary integral equation of the first kind where we use the kernel

(14)

We are only interested in the solution to (13) for the finest space corresponding to the maximal level L. We will use the bilinear form defined as

(15)

(16)

The Gram determinant and its partial derivatives are assumed to be bounded

(17)

(18)

for where for sufficiently large. The Galerkin variational formulation with respect to a finite dimensional space spanned by uses the approximating functions where are the BEM-unknowns. The linear system is eventually obtained such that the matrix entries and the right hand side are respectively

(19)

(20)

The determination of a matrix entry calculates an integration in 4D where the integrand is highly nonlinear and possibly singular depending on the patch pair. By using tensor product B-spline wavelet basis functions, the matrix becomes quasi-sparse. In contrast to the second kind formulation, the weakly singular integral equation produces a symmetric positive definite matrix which is very badly conditioned. Since the stepsize of the discretization is of the form for the maximal level, the smallest and largest eigenvalues [36] for the current 3D problem are as follows

(21)

That means, the condition number increases exponentially as. In this document, we intend to remedy this problem of bad conditioning by using the ASM (Additive Schwarz Method) form of the domain decomposition. It consists in splitting the whole surface into several subdomains. The ASM method is similar to the block Jacobi while the MSM (Multiplicative Schwarz Method) [4] is similar to the block Gauss-Seidel. In contrast to the multiplicative case, the ASM fits very well with parallel computations in practice because every processor can treat its own subdomains with a minimal interprocessor communication. There are two versions of domain decomposition: the overlapping and the non-overlapping ones. We treat in this document the overlapping domain decomposition but the construction of the decomposition starts from a non-overlapping one. In our case, each subdomain constitutes of a set of patches. For a function u defined on the surface and functions defined on the subsurface such that, the key ingredient for a functional domain decomposition method is the following equivalence:

(22)

whose verification is the purpose of this document.

3. Multiscale Wavelet Galerkin Formulation

This section will be occupied by the construction of the nested subspaces (12) on the whole surface. First, we will introduce the subspaces by using the single-scale bases. We present afterward the multi-scale basis which is more efficient with respect to the first kind integral equation. Since we have a four-sided decomposition, constructing the wavelet basis on the unit square is sufficient to form basis functions on the whole surface. On level, we introduce the knot sequence

(23)

The internal knots on the next level are obtained by inserting one new knot inside two consecutive knots on the lower level. Introduce the piecewise constant linear space in the unit interval on level:

(24)

where designates the characteristic function having unit value in D and zero value beyond D. By using the two scale relation

(25)

and the inclusion, the spaces form a nested sequence of subspaces:

(26)

On each patch (), we define the piecewise constant space on level as

(27)

On the whole surface, we define

(28)

with the dimensionalities

(29)

It is deduced from the above construction that we have the inclusion . We will denote the orthogonal projection with respect to the scalar product onto by such that

(30)

Since the single-scale basis functions produce dense matrices, we will introduce another basis which spans the space. On account of the nestedness (26), the space can be expressed as an orthogonal sum

(31)

with respect to the -scalar product where is the complementary wavelet space

(32)

For the explicit expression of the wavelet functions, we use the Haar wavelet defined on by

(33)

whose relation with the single scale basis is such that. By using dilation and shift, one obtains for and

(34)

The wavelet functions constitute an orthonormal basis

(35)

where the first Dirac comes from the inter-level orthogonality while the second Dirac is justified by the non-overlapping of and on the same level. By applying the decomposition (31) recursively, one obtains on the maximal level L

(36)

where

(37)

so that we have the dimensionalities

(38)

A function has two representations: in the single-scale basis and in the multiscale basis, we have respectively

(39)

(40)

The next norm equivalences related to the coefficients are valid [1] [16]

(41)

with constants and independent on the levels. Due to the property (35) and, the orthogonal projection of any onto verifies

(42)

The 2D-wavelet spaces on the unit square is defined for any level as follows

(43)

We have therefore

With respect to the wavelet basis functions, the integrals in (19) and (20) become

(44)

(45)

where

(46)

(47)

Before embarking to the next statement, let us enumerate the 2D-basis which are on different levels. The indices of the basis which are on level or lower are

Similarly for level

As a consequence, the basis indices which are exactly on level are the difference between those lower than and those lower than. That corresponds to

(48)

where

(49)

(50)

(51)

(52)

The following theorem is a collection of properties which enable the subsequent statements.

Theorem 1. (see for e.g. [37] ) We have the continuity and the coercivity of the weakly singular bilinear form with respect to the norm

(53)

(54)

and hence the equivalence

(55)

4. Domain Decomposition for the Wavelet BEM

We will focus in this section on the framework of the ASM domain decomposition. In term of geometric structure, the overlapping domain decomposition will be as follows

(56)

where

(57)

In term of linear spaces, this leads to the decomposition

(58)

where

(59)

On account of the overlapping condition (57), the space decomposition (58) is not necessarily a direct sum. Denote the orthogonal projection onto with respect to the bilinear form from (16) by

(60)

The ASM operator is defined by

(61)

The initial problem (13) is identical [3] to

(62)

The expression of each term of the right hand side b is obtained by locally solving the next equation on the subdomain without explicitly knowing the solution

(63)

where designates the duality pairing between and. The following two criteria are important for the theoretical convergence [3] [38] of the above additive domain decomposition.

(i) For any function, there exist functions such that we have the representation verifying

(64)

for a constant independent of u and.

(ii) For an arbitrary representation such that, there is a constant such that

(65)

If those two criteria (i) and (ii) are satisfied, then we have the following spectral properties of the additive domain decomposition in term of the smallest and largest eigenvalues [3]

(66)

The objective of the next description is to verify those two properties for the BEM bilinear form stemming from the single layer potential as introduced in (16). Our construction of the overlapping decomposition (56) and (57) starts from a non- overlapping decomposition (see Figure 2)

(67)

Figure 2. Domain decomposition of a Water Cluster molecule admitting 1109 patches and 20 non-overlapping subdomains.

Each subdomain which forms a connected subsurface is expanded by additional margin patches to obtain. One margin extension amounts to including the patches which share a node with. That construction is not only important for practical reason but our convergence results depend also on the overlap size

(68)

In the construction, we assume additionally that is nonempty. That is to say, the subdomain is not completely covered by the margins of the other subdomains.

Theorem 2. Consider an overlapping domain decomposition verifying (56) and (57). For an arbitrary on the maximal level L, there exists fulfilling the representation

(69)

such that the single layer bilinear form in (16) satisfies

(70)

Proof. Let us consider any function. We have the representation

(71)

By using the above construction of, the subsurface is nonempty. We define therefore

(72)

By using the orthogonal projections where, we estimate [16] [39]

(73)

(74)

Since constitutes a non-overlapping covering of the whole surface, we obtain

(75)

On the other hand, we have

By using and the inverse inequality [37]

(76)

for piecewise constant functions, we obtain

(77)

Eventually, we conclude from the equivalence (55)

(78)

W

We find in [39] a lengthy deduction of (73) on screen domains whose proof can be extended to curved patches. Another way to obtain (73) for a piecewise constant function in which is as follows. Since,

The operator being a projection, we deduce and hence

One has the next piecewise constant approximation for

(79)

By applying that to, we obtain

(80)

(81)

Lemma 1. Consider two different subdomains and in the overlapping domain decomposition (56) and (57). For a pair of patches such that and and for the 2D-wavelet basis and where and,

(82)

The next estimate is valid

(83)

where the constant c is independent of the maximum level L.

Proof. We have

(84)

where. Since and , one expresses

(85)

By using the primitive of and partial integrations on all four variables, one obtains

(86)

By using the boundedness of the functions, and their derivatives as well as the Calderon-Zygmund estimate, one deduces

(87)

(88)

We use the expression where if and else. On that account, one obtains

(89)

By combining (88) and (89), one deduces from (86)

W

Theorem 3. Consider an overlapping domain decomposition of the surface such as in (56) and (57). For any function, we have on level L the next estimate for the weakly singular potential from (16) in term of the overlap widths

where the constant c is independent of the maximal level L and the overlap widths.

Proof. Let a patch pair be such that and. Consider a function such that

(90)

We intend first to estimate where

(91)

For, one deduces from the Cauchy-Schwarz inequality

In addition, one has [1] [16]

(92)

where and b are respectively the matrix and the vector. As done previously in (92), one has

(93)

where. As a consequence, by using (92), one obtains

(94)

On the other hand, one has the estimate

(95)

On account of the result in (83), one deduces

(96)

Therefore, by using the enumerations of and from (48), one deduces

Consequently, it yields the next estimate

(97)

On account of the fact that

(98)

we deduce

where the last relation was due to the -norm and -norm equivalence. In the same manner as we did in (78), we have the bound

As a consequence, we obtain

(99)

Since, we conclude

(100)

W

Theorem 4. Consider an overlapping domain decomposition verifying

(56) and (57). Consider also a function fulfilling the representation

(101)

By using the bilinear form from (16), we have the next estimation in term of the maximal level L and the margin widths

(102)

where the constant c is independent on the maximal level L.

Proof. We are showing first that. Consider a patch pair such that. Since constitutes a non-overlapping partitioning of, there exists some p such that and some such that. Hence, we have and thus. The opposite inclusion is evident because. Therefore, we obtain

because are mutually disjoint. Further, we have

(103)

where we used in the last equality which holds because is not overlapped by any other subdomain and. Note also that for the same partitioning reason as above and. We deduce therefore

By combining that with (100), we obtain

In the same fashion as in the deduction of (78), we have

(104)

(105)

(106)

Similarly, we have

(107)

As a consequence,

(108)

(109)

By using the -norm and -norm equivalence, we conclude

(110)

W

Corollary 1. Consider an overlapping domain decomposition of the surface verifying (56) and (57). The ASM operator with respect to the weakly singular bilinear form

(111)

verifies on the maximal level L the eigenvalue range

(112)

(113)

and the condition number upper bound

(114)

where the constants, and are independent on the level L.

Proof. Consider an arbitrary representation where. We have

because. Combining that last inequality with (102), we obtain

(115)

(116)

where the constant c is independent on the level L and the functions u,. The bound of the smallest eigenvalue is obtained from (66) and (70). We deduce the estimate of the largest eigenvalue from (66) and (116). The condition number is estimated by

(117)

W

The spectral range might not be optimal yet but our current objective in this document is mainly to eliminate the exponential dependence which was described in (21). In fact, we have the estimate

(118)

which becomes very small as the maximal level L increases. Therefore, the proposed method reduces the upper bound of the condition number from to.

5. Practical Implementation and Numerical Results

In this section, we present some practical results related to the previous theory where we use several molecular models. For the quantum models, we employ Water Clusters and other molecules which are acquired from PDB files. When the molecular dynamic steps attain its equilibrium state where the total energy becomes stable, a water cluster is obtained by extracting the water molecules which are contained in some given large sphere whose radius controls the final size of the Water Cluster. The Hydrogen and Oxygen atoms contained in that large sphere constitute the components of the Water Clusters. The creation of the patch decomposition of the molecular surfaces is performed as described in [24] [40] [23] .

For the practical construction of the domain decomposition on molecular surfaces, we apply a graph partitioning technique. We assemble a graph whose vertices correspond to the patches of the geometry. Two graph vertices and are connected by a graph edge if the corresponding patches and are adjacent. Afterwards, the graph is decomposed into subgraphs. The patches pertaining to each subgraph generate one subdomain in the nonoverlapping domain decomposition. The Water Cluster on Figure 2 is an illustration of the result of such a graph decomposition technique.

We compare in Figure 3 the convergence histories of the direct method and the domain decomposition method. The plots depict the relation between the number of iterations and the residual errors. The quantum model is a Borane containing 432 patches and 100 subdomains. One observes that the number of iterations grow very rapidly in function of the level for the direct method. In contrast, the levels hardly affect the required numbers of iterations for the domain decomposition method. In fact, the iteration counts to drop the error below 10⁻⁹ are respectively 83, 145, 339, 804 for levels 1 till 4 by using the direct method. In order to perceive the plots of the domain decomposition results more clearly, we depict in Figure 4 an enlargement the curves of below iterations 60 where the whole iterations of the direct method cannot be observed. We observe that the errors decrease very quickly for all four levels requiring iteration counts between 28 and 42 by using the domain decomposition technique.

Although it is not the purpose of this document, we summarize in Figure 5(a) the BEM-simulation using single layer potential for a couple of molecules (propane and

Figure 3. Comparison of the direct method and the domain decomposition. Number of iterations vs. residual error.

Figure 4. Close-up of the convergence history of the domain decomposition method for four multiscale levels.

Figure 5. (a) BEM error in function of the maximal level, (b) Density function on a Water Cluster molecule.

Water Cluster) and several right hand-sides. We consider two exact solutions which are respectively and that have vanishing Laplacian. The right hand side is the restriction of the function on the boundary. The curves display the BEM convergence in function of the multiscale level. The error reduction is affected by the exact solutions but in general the errors reduce satisfactorily in function of the wavelet levels. The error plots lightly vary in function of the used molecules but in general all the curves exhibit the same slope characteristic. In fact, they decrease linearly in logarithmic scale in function of the BEM levels. Figure 5(b) exhibits the density function from (13) on the molecular surface where the triangulation is only used for graphical presentation and not for simulation where a Water Cluster molecule is used.

In Table 1, we collect the error reduction of the direct method and the domain decomposition where we consider a Water Cluster which consists of 1109 patches. We gather only some iteration steps where the reduction corresponds to the ratio of two consecutive residuals. The data have been the outcomes of a simulation on the maximal level. We observe that the domain decomposition is very efficient in comparison to the direct method because the error reduction is substantially smaller for the domain decomposition than for the direct method. For the domain decomposition approach, 54 iterations are needed to drop the error below 10⁻⁹ whereas 1007 iterations are required for the direct method to obtain an error of order.

Table 1. Error reductions for Water Cluster admitting 1109 patches at level.

6. Conclusion

We considered the single layer formulation using multiscale wavelet basis where the resulting system is badly conditioned. The additive version of the domain decomposition was used to circumvent the problem of bad conditioning. We concentrated on the non-overlapping domain decomposition where every subdomain is constituted of several patches. The convergence of the corresponding additive Schwarz method was examined. The smallest and the largest eigenvalues as well as the condition number have been estimated. Practical implementations exhibit satisfactory numerical results corresponding to the proposed theory.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Dahmen, W. and Schneider, R. (1999) Wavelets on Manifolds I: Construction and Domain Decomposition. SIAM Journal on Mathematical Analysis, 31, 184-230. http://dx.doi.org/10.1137/S0036141098333451
[2]	Hsiao, H., Steinbach, O. and Wendland, W. (2000) Domain Decomposition Methods via Boundary Integral Equations. Journal of Computational and Applied Mathematics, 125, 521-537. http://dx.doi.org/10.1016/S0377-0427(00)00488-X
[3]	Heuer, N., Stephan, W. and Tran, T. (1998) Multilevel Additive Schwarz Method for the h-p Version of the Galerkin Boundary Element Method. Mathematics of Computation, 67, 501-518. http://dx.doi.org/10.1090/S0025-5718-98-00926-0
[4]	Maischak, M., Stephan, E. and Tran, T. (2004) A Multiplicative Schwarz Algorithm for the Galerkin Boundary Element Approximation of the Weakly Singular Integral Operator in Three Dimensions. International Journal of Pure and Applied Mathematics, 12, 1-21.
[5]	Qiu, T. and Sayas, F. (2016) The Costabel-Stephan System of Boundary Integral Equations in the Time Domain. Mathematics of Computation, 85, 2341-2364. http://dx.doi.org/10.1090/mcom3053
[6]	Baker, N., Sept, D., Holst, M. and McCammon, J. (2001) The Adaptive Multilevel Finite Element Solution of the Poisson-Boltzmann Equation on Massively Parallel Computers. IBM Journal of Research and Development, 45, 427-438. http://dx.doi.org/10.1147/rd.453.0427
[7]	Randrianarivony, M. (2004) Anisotropic Finite Elements for the Stokes Problem: A-Posteriori Error Estimator and Adaptive Mesh. Journal of Computational and Applied Mathematics, 169, 255-275. http://dx.doi.org/10.1016/j.cam.2003.12.025
[8]	Diedrich, C., Dijkstra, D., Hamaekers, J., Henniger, B. and Randrianarivony, M. (2015) A Finite Element Study on the Effect of Curvature on the Reinforcement of Matrices by Randomly Distributed and Curved Nanotubes. Journal of Computational and Theoretical Nanoscience, 12, 2108-2116. http://dx.doi.org/10.1166/jctn.2015.3995.
[9]	Bajaj, C., Xu, G. and Zhang, Q. (2009) A Fast Variational Method for the Construction of Adaptive Resolution Smooth Molecular Surfaces. Computer Methods in Applied Mechanics and Engineering, 198, 1684-1690. http://dx.doi.org/10.1016/j.cma.2008.12.042.
[10]	Cohen, A., Daubechies, I. and Feauveau, J. (1992) Biorthogonal Bases of Compactly Supported Wavelets. Communications on Pure and Applied Mathematics, 45, 485-560. http://dx.doi.org/10.1002/cpa.3160450502
[11]	Lyche, T., Mørken, K. and Quak, E. (2001) Theory And algorithms for Non-Uniform Spline Wavelets, Multivariate Approximation and Applications. Cambridge University Press, Cambridge, 152-187.
[12]	Dahlke, S. and Weimar, M. (2015) Besov Regularity for Operator Equations on Patchwise Smooth Manifolds. Foundations of Computational Mathematics, 15, 1533-1569. http://dx.doi.org/10.1007/s10208-015-9273-9
[13]	Beylkin, G. (1992) On the Representation of Operators in Bases of Compactly Supported Wavelets. SIAM Journal on Numerical Analysis, 29, 1716-1740. http://dx.doi.org/10.1137/0729097
[14]	Kleemann, B., Rathsfeld, A. and Schneider, R. (1996) Multiscale Methods for Boundary Integral Equations and Their Application to Boundary Value Problems in Scattering Theory and Geodesy. Notes on Numerical Fluid Mechanics, 54, 1-28. http://dx.doi.org/10.1007/978-3-322-89941-5_1
[15]	Lage, C. and Schwab, C. (1999) Wavelet Galerkin Algorithms for Boundary Integral Equations. SIAM Journal on Scientific Computing, 20, 2195-2222. http://dx.doi.org/10.1137/S1064827597329989
[16]	Petersdorff, T. and Schwab, C. (1996) Wavelet Approximations for First Kind Boundary Integral Equations on Polygons. Numerische Mathematik, 74, 479-519. http://dx.doi.org/10.1007/s002110050226
[17]	Arioli, M., Kourounis, D. and Loghin, D. (2012) Discrete Fractional Sobolev Norms for Domain Decomposition Preconditioning. IMA Journal of Numerical Analysis, 47, 2924-2951. http://dx.doi.org/10.1137/080729360
[18]	Marcinkowski, L., Rahman, T., Loneland, A. and Valdman, J. (2016) Additive Schwarz Preconditioner for the General Finite Volume Element Discretization of Symmetric Elliptic Problems. BIT Numerical Mathematics, 56, 967-993. http://dx.doi.org/10.1007/s10543-015-0581-x
[19]	Xie, H. and Xu, X. (2014) Mass Conservative Domain Decomposition Preconditioner for Multiscale Finite Volume Method. Multiscale Modeling and Simulation, 12, 1667-1690. http://dx.doi.org/10.1137/130936555
[20]	Randrianarivony, M. (2006) Geometric Processing of CAD Data and Meshes as Input of Integral Equation Solvers. PhD Dissertation, Technical University of Chemnitz, Chemnitz.
[21]	Randrianarivony, M. (2009) On Global Continuity of Coons Mappings in Patching CAD Surfaces. Computer-Aided Design, 41, 782-791. http://dx.doi.org/10.1016/j.cad.2009.04.012
[22]	Harbrecht, H. and Randrianarivony, M. (2010) From Computer Aided Design to Wavelet BEM. Computing and Visualization in Science, 13, 69-82. http://dx.doi.org/10.1007/s00791-009-0129-1
[23]	Harbrecht, H. and Randrianarivony, M. (2009) Wavelet BEM on Molecular Surfaces: Parametrization and Implementation. Computing, 86, 1-22. http://dx.doi.org/10.1007/s00607-009-0050-y
[24]	Randrianarivony, M. and Brunnett, G. (2008) Molecular Surface Decomposition Using Geometric Techniques. Proceedings of Bildverarbeitung für die Medizine, Berlin, 6-8 April 2008, 197-201.
[25]	Weijo, V., Randrianarivony, M., Harbrecht, H. and Frediani, L. (2010) Wavelet Formulation of the Polarizable Continuum Model. Journal of Computational Chemistry, 31, 1469-1477.
[26]	Randrianarivony, M. (2008) Harmonic Variation of Edge Size in Meshing CAD Geometries from IGES Format. Lecture Notes in Computer Science, 5102, 56-65. http://dx.doi.org/10.1007/978-3-540-69387-1_7
[27]	Bramble, J. and Pasciak, J. (1987) New Convergence Estimates for Multigrid Algorithms. Mathematics of Computation, 49, 311-329. http://dx.doi.org/10.1090/S0025-5718-1987-0906174-X
[28]	Bramble, J., Leyk, Z. and Pasciak, J. (1994) The Analysis of Multigrid Algorithms for Pseudo Differential Operators of Order Minus One. Mathematics of Computation, 63, 461-478. http://dx.doi.org/10.1090/S0025-5718-1994-1254145-2
[29]	Gemmrich, S., Gopalakrishnan, J. and Nigam, N. (2012) Convergence Analysis of a Multigrid for the Acoustic Single Layer Equation. Applied Numerical Mathematics, 62, 767-786. http://dx.doi.org/10.1016/j.apnum.2012.02.003
[30]	Harbrecht, H. (2012) Preconditioning of Wavelet BEM by Incomplete Cholesky Factorization. Computing and Visualization in Science, 15, 319-329. http://dx.doi.org/10.1007/s00791-014-0217-8
[31]	Sushnikova, D. and Oseledets, I. (2016) Preconditioners for Hierarchical Matrices Based on Their Extended Sparse Form. Russian Journal of Numerical Analysis and Mathematical Modelling, 31, 29-40. http://dx.doi.org/10.1515/rnam-2016-0003
[32]	Piegl, L. and Tiller, W. (1995) The NURBS Book. Springer, Berlin. http://dx.doi.org/10.1007/978-3-642-97385-7
[33]	Hoschek, J. and Lasser, D. (1996) Fundamentals of Computer Aided Geometric Design. AK Peters Series, Taylor & Francis, London.
[34]	DeBoor, C. and Fix, G. (1973) Spline Approximation by Quasi-Interpolants. Journal of Approximation Theory, 8, 19-45. http://dx.doi.org/10.1016/0021-9045(73)90029-4
[35]	Brunnett, G. (1995) Geometric Design with Trimmed Surfaces. In: Hagen, H., Farin, G. and Noltemeier, H., Eds., Computing Supplement, Vol. 10, Springer, Berlin, 101-115. http://dx.doi.org/10.1007/978-3-7091-7584-2_7
[36]	Pechstein, C. (2013) Special Lecture on Boundary Element Methods Lecture Notes. Institute of Computational Mathematics, Johannes Kepler University of Linz, Linz.
[37]	Nedelec, J. and Planchard, J. (1973) Une méthode variationelle d’éléments finis pour la résolution numérique d'un problème extérieur dans . RAIRO, 7, 105-129.
[38]	Lions, P. (1988) On the Schwarz Alternating Method. In: Glowinski, R., Golub, G.H., Meurant, G.A. and Periaux, J., Eds., First Proceedings of Domain Decomposition Methods for Partial Differential Equations, SIAM, Philadelphia, 1-2, MR 90a: 65248.
[39]	Oswald, P. (1998) Multilevel Norms for . Computing, 61, 235-255. http://dx.doi.org/10.1007/BF02684352
[40]	Randrianarivony, M. and Brunnett, G. (2008) Preparation of CAD and Molecular Surfaces for Meshfree Solvers. Lecture Notes in Computational Science and Engineering, 65, 231-245. http://dx.doi.org/10.1007/978-3-540-79994-8_14