Comparison of Different Models for the Simulation of Photovoltaic Panels ()
Received 3 August 2016; accepted 26 August 2016; published 29 August 2016
1. Introduction
The generation of energy with renewable sources has marked for some years the new road that all the nations must take in order to establish the bases of its energy stability in search of a sustainable development; at present, the balance of the growth of the use of renewable energies is very positive and, in fact, it is even motivating [1] . It goes without saying that the conventional alternatives with which energy is generated, specially speaking about the fossil fuels, are the main source of contamination in the world, that is why the generation of “clean” energy is the best alternative to try to reverse the damage that has been caused to the planet. Because of this fact, this topic has turned into a vital subject for the investigators, in order to develop new and better alternatives for the project implementation [2] ; that’s why the necessary tools to evaluate the performance of these technologies have also been developed taking huge steps.
In the literature, diverse models can be used to represent photovoltaic panels in a circuital form. But nevertheless, the starting point of all is the ideal model [3] , where a parallel between a single diode and a current source is used, as is shown in Figure 1. The complexity of the model will depend on the variables considered,
![]()
Figure 1. Equivalent PV cell electrical circuits, ideal model [3] .
for example the temperature or the degradation, which can influence negatively the energy production of the panels [3] - [5] . Some of the most used models are: “The 4-parameters model”, this one is composed of one-diode with the resistances Rs and Rsh [4] - [7] , and “The 5-parameters model” which have two diodes with Rs and Rsh [3] [5] [8] and [9] . These models were the starting point of the development of this paper.
At present, there is a great variety of programs and tools oriented for the design, the analysis, the diagnosis and even the optimization of the generation with renewable energies. For our case, specifically for the generation of energy through photovoltaic systems, there is a variety of software that allows to realize the measuring of a system, or even the approximation of the performance under adverse operating conditions for photovoltaic panels. It should be noted that the degree of accuracy of these programs will depend largely on the specific function for which they were developed. In several scientific articles it is possible to demonstrate the work developed about this topic [10] - [14] . Some of the more used simulation tools in the academic field are Matlab, Psim and Pspice, since they offer a very comprehensive environment and can be very helpful to realize the simulation and modeling of the photovoltaic panels [15] .
Although many of these programs offer the possibility of modeling, in a circuital way, the photovoltaic panels, or even of using models developed by the creators of programs, such as the MISP, one of the most important factors in a photovoltaic system has not been taken into account, which is the energy production over the time, as it decreases as the years pass. For this reason it is important to predict the behavior of the photovoltaic modules as they age, and get its response through simulation software, taking into consideration actual circumstances of operation which can bring a result that allows a more precise analysis of this behavior.
Out of the programs that were mentioned above, PSIM provides a simple interface and several tools that allow a very precise real behavior of a photovoltaic panel simulation [16] . Furthermore, results can be achieved through elements commonly used in the implementation of circuits, and then the data can be exported to programs that use spreadsheets such as Microsoft Excel, which facilitates the interpretation of the obtained results. For the above mentioned reasons, this software was chosen to realize the simulation.
In order to realize the comparison between the data obtained experimentally with panels of different “ages”, the model proposed in this article, and the existing models that do not include the age of the panel, the expected behavior of a new Photovoltaic Module will be simulated by using the Sim-MFV software, which was developed by members of the Universidad Distrital, in order to obtain the most precise operational curves for the used panels [17] . Since the two programs allow export the achieved results, the goal will be to verify the percentage differences among the proposed model, the existing model and the obtained experimental results.
2. Photovoltaic Panels
A photovoltaic panel is a technological device that allows the production of energy through the photoelectric process by means of sensible semiconductor materials to the sunlight. This device has two curves that characterize it, the first one is Power vs Voltage (P-V) and the second one is Current vs Voltage (I-V). These curves allow us to place the maximum power point of the photovoltaic module.
The curve I-V of the photovoltaic module contains some parameters which affect the functioning of the same; these parameters are: Isc short-circuit current which represents the maximum removable panel current, open circuit voltage Voc, shows the maximum tension when there is no current, Imax is the current of maximum power and Vmax is the voltage of maximum power which is the ideal point of operation of the panel. Following, the typical curves of a panel of 250 W available on the market are shown.
In Figure 2, it can be seen how the value of the generated power increases to a peak and then it decreases rapidly due to the abrupt decrease in the current value. It is important to highlight that the value of the power delivered by the panel will depend on the value of the irradiance to which it is subjected [18] .
One of the most important aspects to consider is the fact that the energy production of the photovoltaic module is gradually reduced over time due to environmental conditions to which is subject such as temperature, humidity, pressure, among others. For this reason manufacturers have a decay curve of energy production, where they perform an approximation of the reduction of the power generated by the photovoltaic panel. An example of this curve is shown in the figure below (Figure 3).
The solar panels can be modeled with electrical circuits as shown in Figure 4, this model can simulate their performance under standard conditions, but it does not take into consideration certain scenarios, such as heating due to power consumption by shading of cells in a single panel. Because the analysis of this paper does not focus on obtaining the maximum power point, but on the behavior of the panel under normal operating conditions, the circuit does not alter the results considerably, so it is not a mistake to use this model. It should be noted that the circuit shown in Figure 4 is the starting point for the model developed in this paper.
3. Models and Simulations
To realize the comparison, three different panels of 10 W, 40 W and 80 W will be used. Their technical specifications are shown in Tables 1-3.
The Sim-MFV program was used to obtain the typical curves of the panel, since this one presents a lower
![]()
Table 1. Technical specifications 10 W panel.
![]()
Table 2. Technical specifications 40 W panel.
![]()
Table 3. Technical specifications 80 W panel.
![]()
Figure 2. Typical curves 230 W Panel phtovoltaic, “I vs V” and “P vs V”.
![]()
Figure 3. Guaranteed Power curve, comparison between different manufacturers [19] .
percentage error with regard to the other simulation models, which can be used as it is demonstrated in [14] . The obtained curves are shown in the Figure 12 where the comparison to the proposed model is shown.
Posed Circuital Model
Since the circuital model shown in Figure 4 does not include the operating time of the panel, a new model derived from it was proposed, but it includes a resistance that we decided to call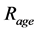
, which refers to the panel “age” and determines the decrease in the output parameters, that is to say, in the current, voltage and power. The proposed model is shown in Figure 5.
With regard to the model shown in Figure 5, where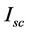 
corresponds to the short circuit current of the panel,
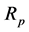represents the resistance associated with leakage currents, 
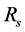is the resistance of contacts and connections and 
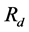represents the PN junction, which can be modeled as a diode which can be represented as a nonlinear resistance [10] [14] . The current through 
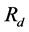is calculated by the following equation:
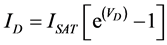(1)
This equation represents the current according to the voltage and was used in 
parameters as shown in Figure 5. Nonetheless, since the value of the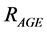 
resistance depends on the operational years of the panel, it is necessary to have a relation between the time variable and the resistance value, for which we have posed the equation (2), which was obtained by means of Lagrange interpolation method where the data obtained experimentally was taken as a starting point.
![]()
(2)
With this equation, it is possible to calculate the value of de ![]()
for any value of time in a rank of to n years, bearing in mind that the lifetime of a panel can exceed 25 years [21] . For this case study, the panels used were made in 2003, 2010, and 2015, so the values of ![]()
were taken, replacing this values we get:
![]()
(3)
![]()
(4)
![]()
Figure 4. Theorical model of the photovoltaic solar panel [20] .
![]()
Figure 5. Posed circuital model (simulated in PSIM).
![]()
(5)
With the value of ![]()
and the values provided by the specification datasheets of each panel, the simulation was realized in PSIM using the developed model. In Figures 6-8 it is possible to observe the circuit, where there are included the values obtained by the equations (3), (4) and (5). Additionally, the results for the curves of operation of each of the panels are shown in Figures 9-11.
It is important to highlight that the model used doesn’t take into consideration the performance of the junction PN in high frequencies, nor the effects due to the temperature. Furthermore, it only describes the performance of the panels to a irradiance value of 1000 W/m2 [14] .
4. Experimental Data and Results
To obtain the practical data, the measurements of voltage and current produced by the panel of 80 W to an approximate irradiance of 1026 W/m2 were performed.
With the information obtained in the measurement the curves of operation of the photovoltaic panel were built, they can be observed in Figures 12-14.
![]()
Figure 6. Circuital model photovoltaic panel 80 W.
![]()
Figure 7. Circuital model for the 40 W photovoltaic panel.
![]()
Figure 8. Circuital model for the 10 W photovoltaic panel.
![]()
Figure 9. Curves obtained with the model developed for the 80 W photovoltaic panel.
![]()
Figure 10. Curves obtained with the model developed for the 40W photovoltaic panel.
In Figures 12-14 operation panel curves can be observed, which obey to the environmental conditions that occurred during the measurement of data, that is to say, to the value of irradiance, ambient temperature, wind speed and other factors which affect measurement.
![]()
Figure 11. Curves obtained with the model developed for the 10 W photovoltaic panel.
Since all software used allow to export data to Microsoft Excel, the comparison figure below was made to see, in a clear way, the difference between the values of the graphs obtained experimentally and the ones obtained by means of simulation.
According to Figures 15-20 the maximum values obtained are shown in Tables 4-6.
To be able to compare more precisely the values obtained in the simulation with the new proposed model, the percentage error was calculated and the results appear in Tables 7-9:
As shown in Tables 7-9 the results provided by the posed model present a margin of extremely less error with regard to the values obtained experimentally, because in it the losses from the operating time of the panel that has been used are taken into account.
5. Conclusions
The posed model represents very closely the real performance of the photovoltaic panels used, since it considers the losses associated with the length of time in operation by means of the value of the resistance.
It is important to highlight that the most approximate datum corresponds to the maximum power that can be extracted from the panel, and that the percentage error with respect to the model that does not include the operating time is below and up to 15%, so the model developed provides very close values which can be used to estimate the actual energy production of the panels, so it could also be used as a tool to develop designing and resizing strategies which are more suitable for the implementation in huge photovoltaic systems, where not only the use of new panels is contemplated.
Maximum current and maximum voltage values are inversely proportional to the power of the simulated panel, i.e. the lower the panel power, the higher the percentage error between these two variables, but the proximity is held with the point of maximum power, which is important because the components that are used in the photovoltaic systems seek the MPPT, and this model is looking to evaluate the energy production of the panel in terms of the maximum power that can be delivered.
In accordance with the obtained results, the proposed model can be the starting point to develop a stronger tool of simulation, where can be considered aspects that degrade the energy production of the panel, for example the temperature and the deterioration produced for the years of operation.
Given that the element representing degradation curves operation is a resistance, it can be used easily in any model. Therefore it can be used to redesign and complement the models of many programs that currently exist.
It is necessary to bear in mind that this model is subject to some restrictions, as for example, the typical values are provided to standard operating conditions, that is to say and 25˚C, which can limit the comparison with the experimental data, since in order to realize a more realistic comparison, the experimental data must be taken under controlled and ideal conditions, so, in these terms, the approach that was realized in this paper is valid, but it increases the error between the simulated and the experimental values.
The development of new elements that complement the modeling of the panels is a fundamental aspect of reengineering simulation tools, because the trend of these developments is directed towards models to describe
![]()
Figure 12. Current vs voltage and power vs voltage, 80 W Panel.
![]()
Figure 13. Current vs voltage and power vs voltage, 40 W Panel.
![]()
Figure 14. Current vs voltage and power vs voltage, 10 W Panel.
![]()
Table 4. Maximum values obtained, 80 W Panel.
*Simulation with a panel at 1000 W/m2; **Measured made approximately at 1026 W/m2.
![]()
Figure 15. Comparing chart, power vs voltage from all the simulated models and from the data measured in practice, 80 W Panel.
![]()
Figure 16. Comparing chart, Current vs Voltage from all the simulated models and from the data measured in practice, 80 W Panel.
![]()
Figure 17. Comparing chart, power vs voltage from all the simulated models and from the data measured in practice, 40 W Panel.
![]()
Figure 18. Comparing chart, Current vs Voltage from all the simulated models and from the data measured in practice, 40 W Panel.
![]()
Figure 19. Comparing chart, power vs voltage from all the simulated models and from the data measured in practice, 10 W Panel.
![]()
Figure 20. Comparing chart, Current vs Voltage from all the simulated models and from the data measured in practice, 10 W Panel.
![]()
Table 5. Maximum values obtained, 40 W Panel.
*Simulation with a panel at 1000 W/m2; **Measured made approximately at 1026 W/m2.
![]()
Table 6. Maximum values obtained, 10 W Panel.
*Simulation with a panel at 1000 W/m2; **Measured made approximately at 1026 W/m2.
![]()
Table 7. Percentage of error with regard to the measurements in condition of operation of the Photovoltaic 80 W Module.
*Values obtained for a new panel.
![]()
Table 8. Percentage of error with regard to the measurements in condition of operation of the Photovoltaic 40 W Module.
*Values obtained for a new panel.
![]()
Table 9. Percentage of error with regard to the measurements in condition of operation of the Photovoltaic 10 W Module.
*Values obtained for a new panel.
the benefits of photovoltaic panels but contemplate all actual parameters that affect the performance and energy production of this renewable technology.