Received 9 June 2016; accepted 15 August 2016; published 18 August 2016

1. Introduction
In 1911, Corrado Gini published his study on the mean introducing an index, later called Gini’s mean difference, as a measure of inequality of a series of values instead of other indexes of variability which measure the spread of the values around a position index. The proposal of Gini is easily extended to the measure of inequality of a random variable. In the most important essays about continuous and discrete distributions [1] [2] no reference can be found to Gini mean difference Δ, while the other variability indexes, in particular the standard deviation and the mean deviation, are widely dealt with. The compact expressions of the mean difference for the normal distribution, for the uniform distribution and for the exponential distribution had long been known. In several recent studies [3] - [8] , compact expressions of the mean difference for almost all the continuous and discrete distribution models have been obtained. About a century after the proposal of Gini, those papers aimed at enhancing an index to measure the variability in the sense of the inequality rather than the spread. The formula of the mean difference of the inverse normal distribution is useful to analyze its relation with the parameters of the model and compare this behavior with those of other variability indexes (standard deviation, mean deviation). Further purpose is to integrate the characterization of the distribution models more than the other indexes of variability do. The above mentioned studies do not treat the formula of the mean difference for the Wald inverse normal distribution. The aim of this paper is to partly fill in this gap.
2. The Inverse Normal Distribution
The density function of the inverse normal distribution is
 (1)
(1)
The cumulative distribution function of the inverse normal distribution is
 (2)
(2)
The cumulative distribution function can also be written as
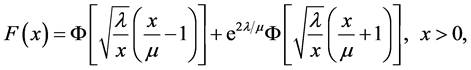 (3)
(3)
in which
 (4)
(4)
is the cumulative distribution function of the standard normal distribution.
The mean and the variance of this distribution are, respectively,
 (5)
(5)
and
 . (6)
. (6)
3. Calculation Procedure for the Mean Difference of a Continuous Distribution
A continuous distribution is characterized by the density function
 , (7)
, (7)
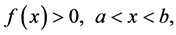 (8)
(8)
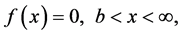 (9)
(9)
or by the cumulative distribution function
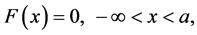 (10)
(10)
 , (11)
, (11)
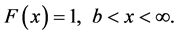 (12)
(12)
Moreover, the first incomplete moment is
 (13)
(13)
 (14)
(14)
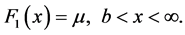 (15)
(15)
In the previous formulas, a can be also equal to ![]() and b equal to
and b equal to![]() .
.
To compute the mean difference of a continuous distribution between the two values x and y of the same random variable, one of the following four formulas can be used.
The direct formula is
![]() (16)
(16)
the formula based on the density function and the cumulative distribution function is
![]() (17)
(17)
another option is the formula based on the density function, the cumulative distribution function and the first incomplete moment is
![]() (18)
(18)
and, finally, the formula based solely on the cumulative distribution function is
![]() (19)
(19)
The previous four formulas are completely equivalent, although, depending on the models whose mean difference has to be calculated, some of them are easier to apply if compared to the others.
4. Calculation Procedure for the Mean Difference of the Inverse Normal Distribution
If we consider the formula based on the cumulative distribution function, the mean difference is
![]() (20)
(20)
Replacing the cumulative distribution function of the inverse normal distribution, leads to
![]() , (21)
, (21)
in which there are the error function
![]() (22)
(22)
and the complementary error function
![]() (23)
(23)
The Error function is encountered in integrating the normal distribution, which is a normalized form of the Gaussian function. Then, introducing the transformation of the variable
![]() (24)
(24)
and denoting
![]() (25)
(25)
this formula is obtained
![]() (26)
(26)
in which the integral depends solely on the parameter ϕ.
The function to be integrated, unless the constant 1/2, has the structure![]() .
.
Introducing the transformation of variable
![]() (27)
(27)
after heavy but direct calculations, the following expression is achieved
![]() (28)
(28)
For simplicity, in the above formula the following transformation of the variable should be introduced
![]() (29)
(29)
which, after further heavy but direct calculations, leads to
![]() (30)
(30)
in which the integral exists for any value of μ and for φ > 0. The analytical value of Δ is not known but its value can be easily numerically calculated.
The obtained expression is the simplest formula enabling to compute the mean difference of the inverse normal distribution. The above formula clearly highlights the role of the two parameters: one, μ, is a multiplicative factor and the other one, ϕ, is part of the function to be integrated.
Figure 1 shows the trend of the mean difference of the inverse normal distribution as function of the parameters μ and ϕ. It can be observed that Δ increases with the parameter μ and decreases as the parameter ϕ increases.
Through a transformation of variable or an integration by parts, several other equivalent formulas can be obtained, all of them needing an integration. Some of them are shown in the Appendix.
![]()
Figure 1. Trend of the mean difference Δ of inverse normal distribution as function of the parameters μ and ϕ.
5. Conclusive Remarks
In this paper, a simple formula of the mean difference of the inverse normal distribution is achieved. The formula is simpler than those obtainable by a transformation of variable or an integration by parts of the same. Even if the formula contains an integration to be computed, it is undoubtedly easy to calculate and allows to highlight the role of the two parameters on the mean difference of the model. It makes it easier to study the relation of the mean difference with the other indexes of variability for the inverse normal distribution.
Appendix: Alternative Formulas for Calculating Δ for the Inverse Normal Distribution
![]() (31)
(31)
![]() (32)
(32)
![]() (33)
(33)
![]() (34)
(34)
![]() (35)
(35)
![]() (36)
(36)
![]() (37)
(37)
![]() (38)
(38)
![]() (39)
(39)
![]() (40)
(40)
![]() (41)
(41)
![]() (42)
(42)
![]() (43)
(43)
Attributions Girone Sections 1, 2, 3 and the Appendix, D’Uggento Sections 4 and 5.