Proofs of the Density Theorem and Fatou’s Radial Limit Theorem Using the Poisson Integral ()

Subject Areas: Function Theory

1. Introduction
In most texts, [1] (p. 261), [2] (p. 187), [3] (p. 129), to name a few, the Density Theorem is proven using the fact that if f is Lebesgue integrable and if σ = òf, then σ¢ = f a.e. This result in turn is proven using the Vitali Covering Theorem. The same procedure is also used in the proof of Fatou’s radial limit theorem (see [4] , p. 129, and [5] , Vol. II, p. 362-364). We circumvent this reasoning in an attempt to make the Density and Fatou theorems more accessible to the reader. Our major reference will be Royden’s book Real Analysis, and we will restrict ourselves to its first four chapters. These include a general introduction to set theory, the real number system, Lebesgue measurable functions, and the Lebesgue integral. Our major analytical tool will be the Poisson integral and we will use some of its well-known fundamental properties.
We first introduce the background material that will be used in the course of this note. Our setting is the unit disk D and its boundary C. We shall say that a sequence {Ik} of arcs in C converges to  and write Ik ® eiθ,
and write Ik ® eiθ, 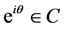 , if
, if  for each k and
for each k and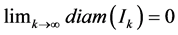 . Let A be any subset of C and let m* and m denote respectively the outer Lebesgue measure and the Lebesgue measure on C. For any measurable set E in C we define
. Let A be any subset of C and let m* and m denote respectively the outer Lebesgue measure and the Lebesgue measure on C. For any measurable set E in C we define . We shall say that the derivative of σA at eiθ exists if there exists a number
. We shall say that the derivative of σA at eiθ exists if there exists a number 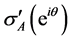 such that for any sequence {Ik} of arcs converging to eiθ,
such that for any sequence {Ik} of arcs converging to eiθ,
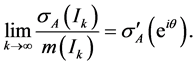
If , eiθ is called a point of density of A and if
, eiθ is called a point of density of A and if , eiθ is called a point of dispersion of A.
, eiθ is called a point of dispersion of A.
The Density Theorem states that if A is any set (measurable or not) in C, then eiθ is a point of density for A for almost all eiθ in A. We shall prove that this result in the case A is measurable.
Let u(z), 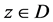 , be defined by the Poisson integral,
, be defined by the Poisson integral,
 (1)
(1)
where 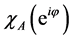 is the characteristic function on the measurable set
is the characteristic function on the measurable set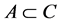 , and
, and
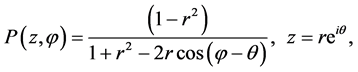
is the Poisson kernel. When A is a finite union of open arcs, then χA is a bounded piecewise continuous function on C. So, if ξ is a point of continuity of χA, then a straight-forward examination of the integral in (1) shows that the limit of u(z), as z approaches ξ exists and equals χA(ξ) (see [6] , Vol. II, p. 156; [7] , p. 206; and [4] , p. 130). The kernel has two nice properties:
i) 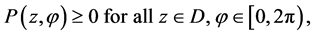 and
and
ii) ![]() (see [8] , p. 165-167 and [9] , p. 305-307).
(see [8] , p. 165-167 and [9] , p. 305-307).
It follows that ![]() for all
for all![]() . We will use these elementary results in Sections 2 and 3.
. We will use these elementary results in Sections 2 and 3.
2. The Density Theorem
Theorem: Let A be measurable. Then almost every point of A is a point of density of A.
Proof: Let B be those points of A that are not points of density of A; that is,
![]()
where Iδ, δ > 0, denotes an arc containing eiθ having length δ. For each![]() , let
, let![]() . We will first show that B can be rewritten as
. We will first show that B can be rewritten as
![]()
where ![]() is an arc centered at eiθ with length 2ξk such that ξk → 0 as k → ∞. This reformulation of B is
is an arc centered at eiθ with length 2ξk such that ξk → 0 as k → ∞. This reformulation of B is
crucial to our proof. Clearly, any point in this set is in B. Now suppose![]() . Then there exists a positive number ε and a sequence {δn} such that δn ® 0 as n ® ¥ and
. Then there exists a positive number ε and a sequence {δn} such that δn ® 0 as n ® ¥ and
![]()
For each n let sn denote the length of the largest component of ![]() and choose kn such that
and choose kn such that![]() . Then
. Then
![]()
Since the last expression approaches 1 − ε/2 as kn ® ¥, it follows that
![]()
Using this reformulation of B, the facts that for each k, ![]() is a continuous function of θ and consequently measurable, theorem 20 in [10] (p. 56), and that A is a measurable set, it readily follows that B is a measurable set. Hence, it is the union of an F-σ set and a set N of measure zero; that is,
is a continuous function of θ and consequently measurable, theorem 20 in [10] (p. 56), and that A is a measurable set, it readily follows that B is a measurable set. Hence, it is the union of an F-σ set and a set N of measure zero; that is, ![]()
where each Fn is a closed subset of B. If we show each Fn has measure zero, then the theorem is proved. We pick a Fn and denote it by F in order to avoid layered subscript notation. Now![]() , where Ok are pairwise
, where Ok are pairwise
disjoint open arcs. For each![]() , let
, let![]() , χn be the characteristic function of Dn, and set
, χn be the characteristic function of Dn, and set ![]() for
for![]() . Note that for all n,
. Note that for all n, ![]() , and
, and![]() . We know from our introductory remarks that except for a finite number of eiθ on C,
. We know from our introductory remarks that except for a finite number of eiθ on C,![]() . Let Sn denote this exceptional set. If we set
. Let Sn denote this exceptional set. If we set![]() , then for all
, then for all ![]() and for all n,
and for all n,
![]() (2)
(2)
Also, for all eiθ Î C,
![]() (3)
(3)
We now show that m(F) = 0 using an indirect argument. Before we formally proceed we indicate the direction our proof will take: We define the Poisson integral of the characteristic function on F and using Equations (2) and (3), along with the assumption that F has positive measure, find a subset of F where the radial limit of this function is 1. We then use the reformulation of B to show that this cannot happen.
So, suppose that m(F) > 0. Momentarily fix θ. For each![]() , define
, define![]() . Then rk ® 1 as k ® ¥. Since for each k,
. Then rk ® 1 as k ® ¥. Since for each k, ![]() is a nonnegative and integrable function of j, we have ( [10] , p. 73) that for each ξk there exists δk > 0 such that if E is any set with m(E) < δk, then
is a nonnegative and integrable function of j, we have ( [10] , p. 73) that for each ξk there exists δk > 0 such that if E is any set with m(E) < δk, then
![]() (4)
(4)
For each![]() , let
, let![]() . Using Egorov’s Theorem ( [10] , p. 59), we have for each k an open set Mk such that
. Using Egorov’s Theorem ( [10] , p. 59), we have for each k an open set Mk such that
![]() and
and![]() uniformly on Mk. (5)
uniformly on Mk. (5)
Note that![]() , and since S is at most countable,
, and since S is at most countable, ![]() has positive measure. Set
has positive measure. Set![]() .
.
We now claim that if eiθ is in![]() , then
, then![]() . Let ε be an arbitrary positive number and choose K such that for k > K, ξk < ε/4. Now for k > K,
. Let ε be an arbitrary positive number and choose K such that for k > K, ξk < ε/4. Now for k > K,
![]()
Since χn converges uniformly to χF on Mk we choose N = N(ε) such that ![]() on Mk. Thus,
on Mk. Thus,
![]()
Using (4) with the fact that ![]() one also has
one also has
![]()
Hence, ![]() for all k > K. Because
for all k > K. Because![]() , Equation (2) holds. In addition, we have for all n that χn = χF on F. Consequently, for k sufficiently large,
, Equation (2) holds. In addition, we have for all n that χn = χF on F. Consequently, for k sufficiently large,
![]()
and since ε was arbitrary, our claim is established.
However, using the reformulation of B we know that since ![]() and
and![]() , there exists a positive number η and a subsequence
, there exists a positive number η and a subsequence ![]() of arcs with the property that
of arcs with the property that
![]()
Since![]() , we have
, we have
![]()
Since the last expression approaches η/2π as ![]() or as
or as![]() , we have that the
, we have that the
![]()
and this contradicts our previous claim. Thus, the measure of F cannot be positive and so m(F) = 0.
3. Density and the Radial
In this section we establish relationships between the density of A at a point of C and the radial limit of the Poisson integral of the characteristic function on A at this point. The proofs of the first two theorems employ well-known procedures and inequalities. Theorem 3 highlights the last result in the proof of the Density Theorem. We then use these relationships and prove in Corollary 5 Fatou’s radial limit theorem.
Theorem 1. If eiθ is a point of density of A and u(z) represents the Poisson integral of![]() , then the radial limit of u(z) at eiθ is 1.
, then the radial limit of u(z) at eiθ is 1.
Proof: Without loss of generality we can assume eiq = ei0 = 1 and we express the Poisson integral of χA over the interval [−π, π] instead of [0, 2π]. We must show that![]() .
.
Since 1 is a point of density of the measurable set A, it follows that 1 is a point of dispersion of AC, the complement of A with respect to C. Letting![]() , where Iδ(1) denotes the arc on C centered at 1with length 2δ, we know that ε(δ) ® 0 as δ ® 0. Let z = r. Then
, where Iδ(1) denotes the arc on C centered at 1with length 2δ, we know that ε(δ) ® 0 as δ ® 0. Let z = r. Then
![]() (6)
(6)
There are two possibilities that can happen with the function ε(δ), δ > 0. Either there exists a δ0 such that ε(δ0) = 0; or for all δ, ε(δ) ≠ 0.
In the first case it follows that ![]() for all
for all![]() . We now rewrite (6) as
. We now rewrite (6) as
![]()
In the first integral we know that![]() ; and for
; and for![]() ,
,![]() . Hence, the integral is zero. For the second integral we have that
. Hence, the integral is zero. For the second integral we have that ![]() and so
and so![]() . Now
. Now
![]()
On [0, π/2] we have that sin(x) ≥ (2/π)x. So if r > 1/2 we get![]() , and hence
, and hence
![]()
The third integral is handled like the second, and so our theorem follows.
In the second case it follows that if δ is sufficiently small, ![]() is a continuous increasing function of δ. So there exists a δ0 such that the expression
is a continuous increasing function of δ. So there exists a δ0 such that the expression ![]() is continuous and increasing
is continuous and increasing
on (0, δ0). Consequently, the expression ![]() is a continuous increasing function of δ on (0, δ0) with the
is a continuous increasing function of δ on (0, δ0) with the
property that ![]() as δ→0. Using this result we know that as r ® 1, 1 − r ® 0 and so it can be
as δ→0. Using this result we know that as r ® 1, 1 − r ® 0 and so it can be
represented by ![]() for some δr. Furthermore, 1 - r ® 0 iff δr ® 0. On the interval [−δr, δr] we use the inequality
for some δr. Furthermore, 1 - r ® 0 iff δr ® 0. On the interval [−δr, δr] we use the inequality ![]() to get
to get
![]()
We now rewrite (6) as was done in the first case but using δr instead of δ0. The first integral is handled above. The second integral is handled exactly as before. We get
![]()
The third integral is handled like above. Hence, our theorem follows. Using a similar argument we can obtain the second result of this section.
Theorem 2. If eiθ is a point of dispersion of A, then the radial limit of u(z) at eiθ is 0.
Theorem 3. If eiθ is neither a point of density of A nor a point of dispersion of A, then the radial limit, if it exists, cannot be 1 or 0.
Proof: From the hypothesis we know there exists an ε > 0 and two sequences ![]() of arcs, where δn and ρn denote the length of
of arcs, where δn and ρn denote the length of ![]() and
and ![]() respectively, such that
respectively, such that ![]() for all n,
for all n, ![]() for all n,
for all n,
![]() for all n,
for all n,
![]() for all n,
for all n,
and δn ® 0 and ρn ® 0 as n ® ¥. Since the arcs are not centered at eiθ we define ξn to be the maximum of the lengths of the components of ![]() and define
and define ![]() to be the arc centered at eiθ with length 2ξn. Using
to be the arc centered at eiθ with length 2ξn. Using ![]() we define τn similarly. Let
we define τn similarly. Let ![]() and
and![]() . Then,
. Then,
![]()
Since the last expression approaches ε/4π as ξn ® 0 or as rn ® 1, we have that the
![]() (7)
(7)
A similar argument using ![]() shows that the
shows that the![]() . It follows that if the radial limit of u(z) at eiθ exists, then it cannot be 1 or 0.
. It follows that if the radial limit of u(z) at eiθ exists, then it cannot be 1 or 0.
Corollary 1: Let A be any measurable set in C. Let ![]() Then for almost every eiθ Î C,
Then for almost every eiθ Î C,![]() .
.
Proof: Using the Density Theorem on A and Theorem 1, we have for almost every eiθ in A,![]() . Since AC is also measurable we have that almost every point of AC is a point of density of AC. Hence, almost every point of AC is a point of dispersion of A. By Theorem 2 we have that for almost every eiθ in AC,
. Since AC is also measurable we have that almost every point of AC is a point of density of AC. Hence, almost every point of AC is a point of dispersion of A. By Theorem 2 we have that for almost every eiθ in AC,![]() .
.
Corollary 2: Let f be a simple function defined on C. Let ![]() Then for almost every eiθ Î C,
Then for almost every eiθ Î C, ![]()
Proof: If f is simple, then ![]() where the Ai are pair-wise disjoint and measurable and the ai are distinct and nonzero. Using Corollary 1, our result follows.
where the Ai are pair-wise disjoint and measurable and the ai are distinct and nonzero. Using Corollary 1, our result follows.
Corollary 3: Let f be a bounded measurable function defined on C. Let ![]() Then for almost every eiθ Î C,
Then for almost every eiθ Î C, ![]()
Proof: Since f is bounded and measurable, there exists simple functions ψn, ψn £ f, such that ![]() uniformly on C. By adding and subtracting the appropriate terms and using the triangle inequality one can show that
uniformly on C. By adding and subtracting the appropriate terms and using the triangle inequality one can show that
![]()
We analyze each term on the right hand side of this inequality. Since the kernel P(z, j) is non-negative and its definite integral is 2π (see Section 1), and since ψn converges uniformly to f on C, the first term can be made arbitrarily small when n is sufficiently large. From Corollary 2 we get that the second term can be made arbitrarily small as r approaches 1. The last term approaches 0 for n sufficiently large since ψn converges uniformly to f on C. Consequently, our result follows.
Corollary 4: Let f be a nonnegative integrable function defined on C. Let ![]() Then for almost every
Then for almost every![]() ,
, ![]()
Proof: Let![]() . Since f is integrable we know that m(S) = 2π. For each
. Since f is integrable we know that m(S) = 2π. For each![]() , define
, define![]() . Each fn is bounded, nonnegative, and measurable on S. The functions also satisfy the following on S:
. Each fn is bounded, nonnegative, and measurable on S. The functions also satisfy the following on S: ![]() and
and ![]() Since P(z, j) is non-negative we have that
Since P(z, j) is non-negative we have that ![]() and hence
and hence ![]() on S. By the Monotone Convergence Theorem ( [10] , p. 72) we know that
on S. By the Monotone Convergence Theorem ( [10] , p. 72) we know that
![]()
Once again, by adding and subtracting the appropriate terms and using the triangle inequality one can show that
![]()
From our above remarks, the first term can be made arbitrarily small for n sufficiently large. Using Corollary 3, the second term can be made arbitrarily small as r approaches 1. The last term approaches 0 on S as n gets large. Consequently, our result follows.
Corollary 5: (Fatou) Let f be integrable on C. Let ![]() Then for almost every eiθÎC,
Then for almost every eiθÎC, ![]()
Proof: We know that ![]() where
where ![]() and
and![]() . Since f is integrable, both
. Since f is integrable, both ![]() and
and ![]() must be integrable. We can now use Corollary 4 on
must be integrable. We can now use Corollary 4 on ![]() and
and ![]() to get our result.
to get our result.